那么插入排序的时间复杂度是多少呢？答案是：O(N ^ 2)，并不是因为它是双重循环，计算时间复杂度要看最坏的情况，而插入排序最坏的情况其实就是逆序，每个arr[end + 1]都要从头到尾遍历一遍，1 + 2 + 3 + ... + n - 1，是个等差数列，计算结果是 n ^ 2 / 2，取增长最快的那个，就是n ^ 2了。最好的情况就是该数列已经是升序的情况，此时时间复杂度是 O(N)。

// 直接插入排序
void InsertSort(int* arr, int n){
  // i最大是倒数第二个数的下标
  for(int i = 0; i < n - 1; i++){
    int end = i;
    int tmp = arr[end + 1];
    while(end >= 0){
      // 如果arr[end]的值比tmp大，让它后移一位
      if(arr[end] > tmp){
        arr[end + 1] = arr[end];
        end--;
      }else{
        // 如果arr[end]的值比tmp小，跳出循环
        break;
      }
    }
    // 让end+1上面的值变为tmp
    arr[end + 1] = tmp;
  }
}

void testInsertSort(){
  int arr[] = { 4, 9, 2, 6, 1, 8, 7, 3, 5, 0 };
  InsertSort(arr, sizeof(arr) / sizeof(int));
  PrintArray(arr, sizeof(arr) / sizeof(int));
}

int main(){

  testInsertSort();

  return 0;
}

2. 希尔排序

希尔排序实质上就是在直接插入排序之前加上了一步“预排”，所谓“预排”就是让大的数尽可能到后面，小的数尽可能快的到前面，以下面这幅图为例，我们设置gap为3，这样使得每隔gap距离的数字为一组，下面就是 [ 4, 6, 7, 0 ]，[ 9, 1, 3?]，[ 2, 8, 5 ] 这三组，按照直接插入排序的方式，先创建一个变量保存arr[end + gap]，判断arr[end]是否大于tmp，如果大于就往后移一位，让 end 减等 gap，如果小于就跳出循环，不管是大于还是小于，最终都要让arr[end + gap]赋值为tmp，这样再让gap为2，再让gap为1，最终就是以升序排列的

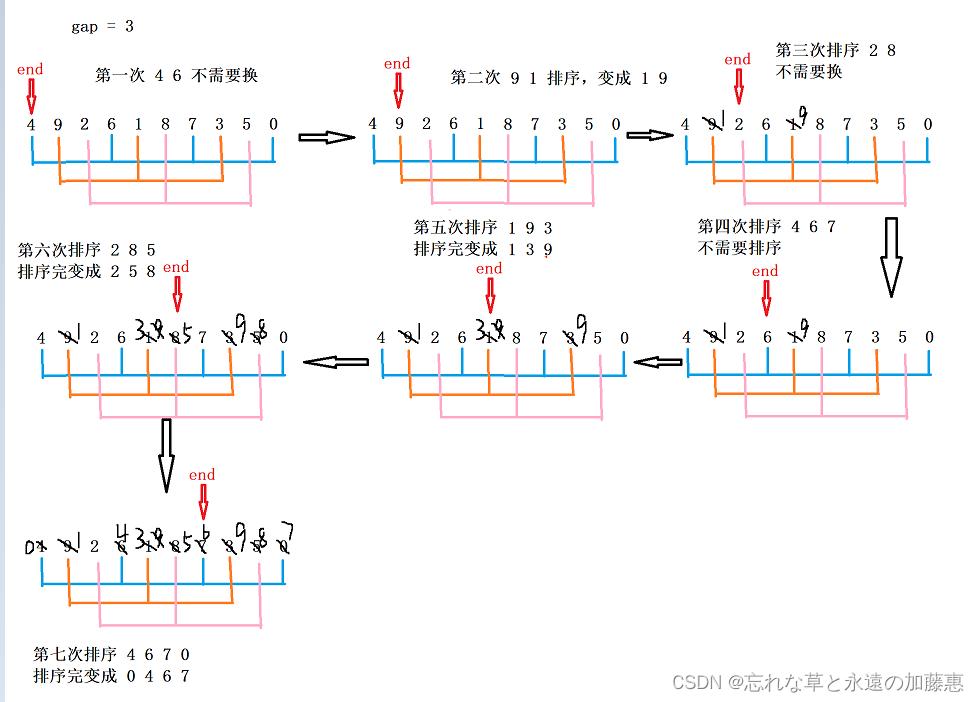
?代码实现如下，对于gap要选好值，最终必须让gap为1进行一次排序，可以让gap每次除等2，也可以每次除等3再加上1

void ShellSort(int* arr, int n){
  int gap = n;

  while(gap > 1){

    // gap > 1 都是预排，让他的顺序接近有序
    // gap = 1 时，实质上就是直接插入排序
    // gap /= 2;
    gap = gap / 3 + 1; // 要让最后一次排序的时候gap为1

    for(int i = 0; i < n - gap; i++){
      int end = i;
      int tmp = arr[end + gap];
      while(end >= 0){
        if(arr[end] > tmp){
          arr[end + gap] = arr[end];
          end -= gap;
        }else{
          break;
        }
      }
      arr[end + gap] = tmp;
    }
  }

}

void TestShellSort(){
  int arr[] = { 4, 9, 2, 6, 1, 8, 7, 3, 5, 0 };
  ShellSort(arr, sizeof(arr) / sizeof(int));
  PrintArray(arr, sizeof(arr) / sizeof(int));
}

int main(){
  TestShellSort();
  return 0;
}

希尔排序的时间复杂度是O(logN * N)，具体的证明这里不做描述，可以自行去推理或者去网上搜。

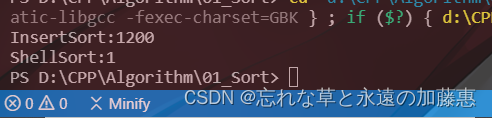
既然说希尔排序比直接插入排序优秀，那么到底是什么样的呢，可以运行如下代码进行测试，它可以计算100000个随机数排序所花费的时间

void testOP(){
  srand((unsigned int)time(NULL));

  const int N = 100000;

  int* a1 = (int*)malloc(sizeof(int) * N);
  int* a2 = (int*)malloc(sizeof(int) * N);

  for(int i = 0; i < N; i++){
    a1[i] = rand();
    a2[i] = a1[i];
  }

  int begin1 = clock();
  InsertSort(a1, N);
  int end1 = clock();

  int begin2 = clock();
  ShellSort(a1, N);
  int end2 = clock();

  cout << "InsertSort:" << end1 - begin1 << endl;
  cout << "ShellSort:" << end2 - begin2 << endl;

  free(a1);
  free(a2);
}

int main(){

  testOP();

  return 0;
}

运行结果如下：直接插入排序花费了 1200 ms，希尔排序花费了 1ms，差距很大，足以说明希尔排序比直接插入排序更加的优秀。

3. 堆排序

堆的逻辑结构是一颗完全二叉树，物理结构是数组，要实现这个排序，需要把数组想象成堆，比如下面这幅图，它一个数组变成想象成一个堆

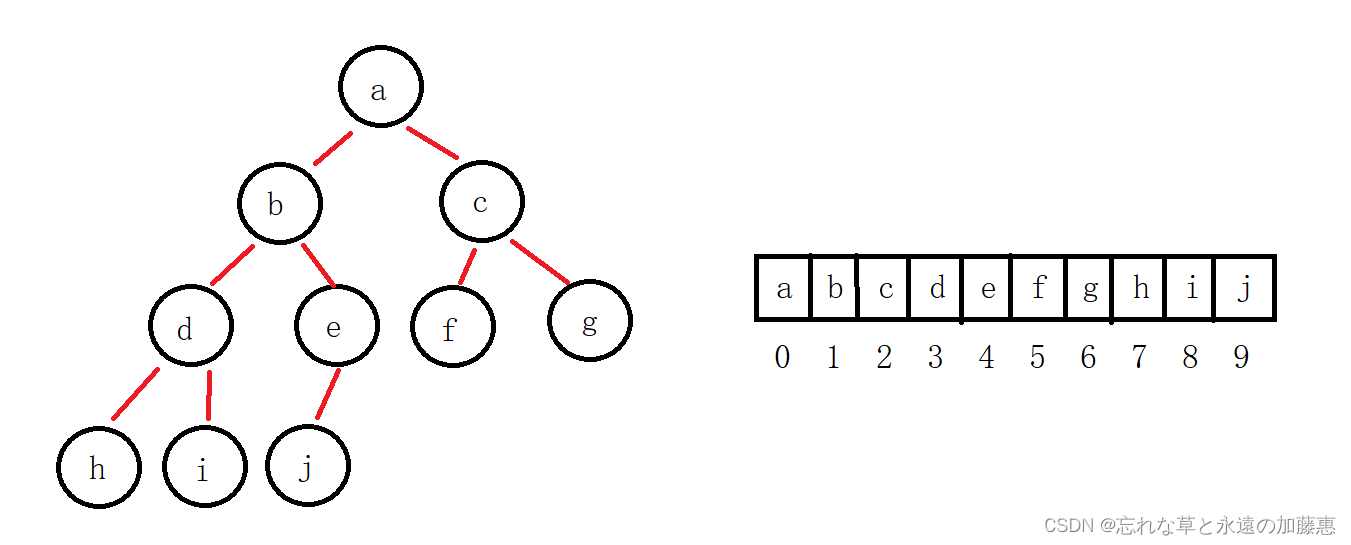
根据这幅图和数组以及下标可以的得出来一个结论：左子节点的下标 = 父节点的下标 * 2 + 1，右子节点的下标 = 父节点的下标 * 2 + 2，父节点的下标 = （子节点的下标 - 1）/ 2，不管是左子节点还是右子节点都满足这个公式，在实现堆排序是需要先讲一个东西——向下调整算法

向下调整算法：

? ? ? ? 向下调整的目的是为了建小堆或建大堆

? ? ? ? 建小堆：所有的子节点都比父节点大

? ? ? ? 建大堆：所有的子节点都比父节点小

这幅图最后的结果就是它是个小堆

但其实这是一种特殊的情况，因为根节点的左右子树已经都是小堆了，而如果它是无序的，那我们就要从0构建小堆，也就是要用一个循环，从倒数第一个非叶子节点开始，把他变成一个小堆，然后一直直到根节点?

实现代码如下：

// 向下调整算法
// 建小堆
void AdjustDown(int* arr, int n, int root){
  // 默认左子节点为孩子
  int parent = root;
  int child = parent * 2 + 1;
  // 如果child比数组的长度小，就可以向下调整
  while(child < n){
    // 如果右子节点的数小于左子节点的数，让child++，但是前提必须有右子节点
    if(child + 1 < n && arr[child + 1] < arr[child]){
      child++;
    }
    if(arr[child] < arr[parent]){
      // 如果子节点的数比父节点小，让他们交换
      swap(arr[child], arr[parent]);
      // 让原来的子节点变成父节点，继续向下调整
      parent = child;
      child = parent * 2 + 1;
    }else{
      // 如果子节点的数大于父节点的数，跳出循环
      break;
    }
  }
}
void HeapSort(int* arr, int n){
  for(int i = (n - 1 - 1) / 2; i >= 0; i--){
    AdjustDown(arr, n, i);
  }
}

如果是要建大堆的话是需要变 < 为 >，实现代码如下：

// 向下调整算法
// 建大堆
void AdjustDown(int* arr, int n, int root){
  // 默认左子节点为孩子
  int parent = root;
  int child = parent * 2 + 1;
  // 如果child比数组的长度小，就可以向下调整
  while(child < n){
    // 如果右子节点的数小于左子节点的数，让child++，但是前提必须有右子节点
    if(child + 1 < n && arr[child + 1] > arr[child]){
      child++;
    }
    if(arr[child] > arr[parent]){
      // 如果子节点的数比父节点小，让他们交换
      swap(arr[child], arr[parent]);
      // 让原来的子节点变成父节点，继续向下调整
      parent = child;
      child = parent * 2 + 1;
    }else{
      // 如果子节点的数大于父节点的数，跳出循环
      break;
    }
  }
}
void HeapSort(int* arr, int n){
  for(int i = (n - 1 - 1) / 2; i >= 0; i--){
    AdjustDown(arr, n, i);
  }
}

那么为了实现升序，我们是要建大堆还是小堆呢？

相信如果你不懂它的实现原理的话会觉得要建小堆，但事实上是要建大堆

它的实现原理是这样的：

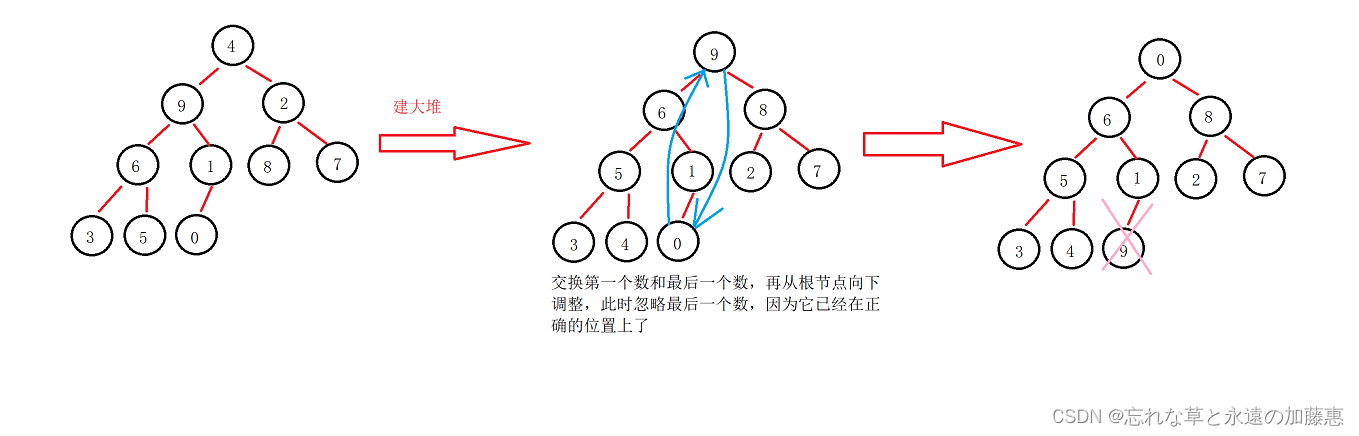
当建大堆完成后，此时根节点就是最大的的数，交换第一个数和最后一个数，此时最大的数已经在最后面了，也就是说最大的数已经在正确的位置上了，此时再从根节点向下调整，并不是再次建大堆，而是直接向下调整，因为此时根节点的左右子树都已经是大堆了，但是这次向下调整要忽略最后一个数，就这样循环，直到根节点为止

?实现代码如下：

// 向下调整算法
void AdjustDown(int* arr, int n, int root){
  // 默认左子节点为孩子
  int parent = root;
  int child = parent * 2 + 1;
  // 如果child比数组的长度小，就可以向下调整
  while(child < n){
    // 如果右子节点的数小于左子节点的数，让child++，但是前提必须有右子节点
    if(child + 1 < n && arr[child + 1] > arr[child]){
      child++;
    }
    if(arr[child] > arr[parent]){
      // 如果子节点的数比父节点小，让他们交换
      swap(arr[child], arr[parent]);
      // 让原来的子节点变成父节点，继续向下调整
      parent = child;
      child = parent * 2 + 1;
    }else{
      // 如果子节点的数大于父节点的数，跳出循环
      break;
    }
  }
}

// 堆排序
void HeapSort(int* arr, int n){
  for(int i = (n - 1 - 1) / 2; i >= 0; i--){
    AdjustDown(arr, n, i);
  }

  int end = n - 1;
  while(end > 0){
    swap(arr[0], arr[end]);
    AdjustDown(arr, end, 0);
    end--;
  }
}

void TestHeapSort(){
  int arr[] = { 4, 9, 2, 6, 1, 8, 7, 3, 5, 0 };
  HeapSort(arr, sizeof(arr) / sizeof(int));
  PrintArray(arr, sizeof(arr) / sizeof(int));
}

int main(){

  TestHeapSort();

  return 0;
}

那么下面阐述一下为什么不能建小堆：

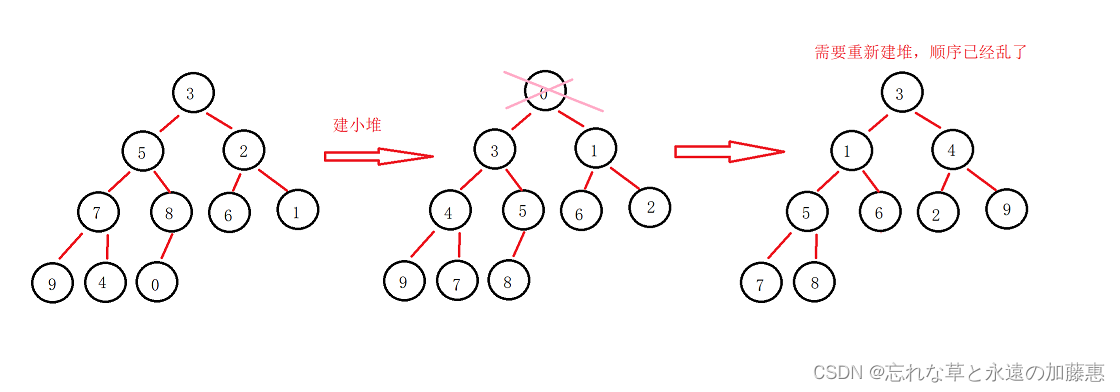
如下图所示，建小堆之后，最小的数在第一个了，此时也不需要进行交换，它的位置已经是正确的了，也就是说需要把后面的所有节点都要在进行一次建小堆，因为此时它的顺序已经被打乱了，此时时间复杂度是O(N^2)，效率太低，而这就失去了它的优越性，因此要建大堆

4. 直接选择排序

直接选择排序应该是最容易理解，性能也是最差的了，原理很简单，从头开始，往后遍历，找到最小的数，和第一个数调换，循环执行

?实现代码如下：

// 直接选择排序
void SelectSort(int * arr, int n){
  for(int i = 0; i < n; i++){
    int min = i;
    for(int j = i + 1; j < n; j++){
      if(arr[j] < arr[min]){
        min = j;
      }
    }
    swap(arr[i], arr[min]);
  }
}

?但是其实上面的代码还可以优化，上面是每次选出最小的数放在前面，那么可以同时选最小的数放前面，最大的数放后面，如下图所示，但是这里有个注意点，就是maxIndex的值可能会需要修正，具体见代码：?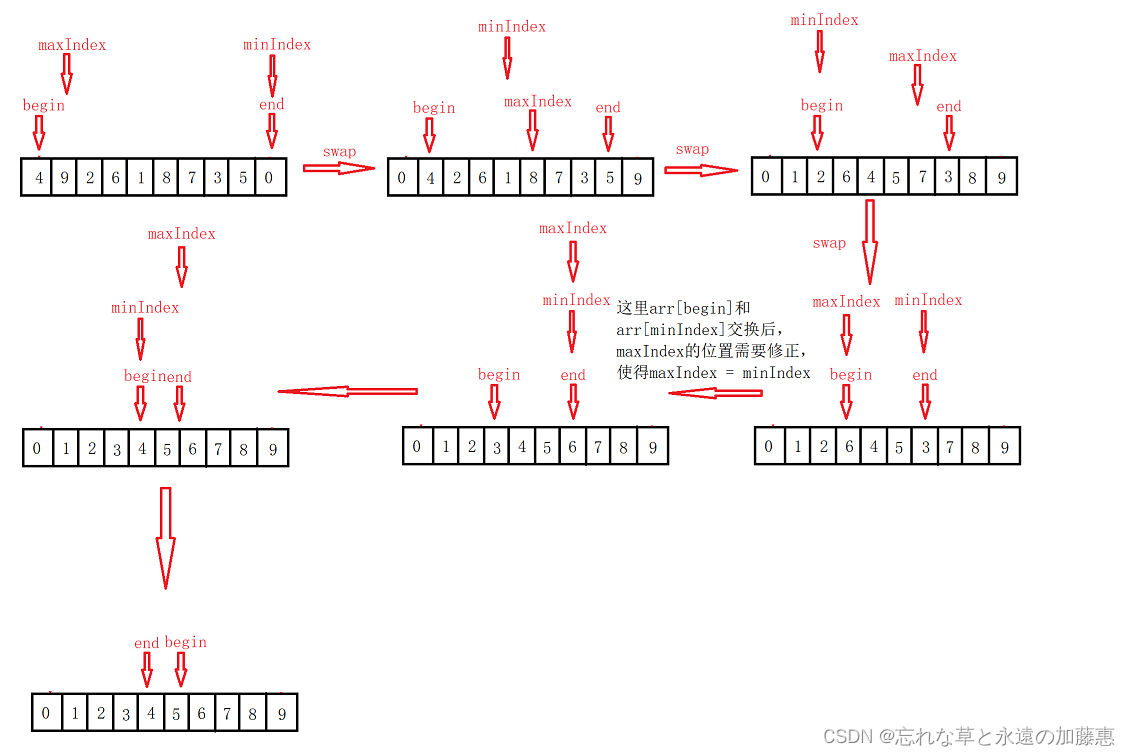

?代码如下：

// 直接选择排序
void SelectSort(int * arr, int n){
  int begin = 0, end = n - 1;
  while(begin < end){
    int minIndex = begin, maxIndex = begin;
    for(int i = begin; i <= end; i++){
      if(arr[i] < arr[minIndex]){
        minIndex = i;
      }
      if(arr[i] > arr[maxIndex]){
        maxIndex = i;
      }
    }
    
    swap(arr[begin], arr[minIndex]);
    if(maxIndex == begin){
      maxIndex = minIndex;
    }
    swap(arr[end], arr[maxIndex]);
    begin++;
    end--;
  }
}

5. 冒泡排序

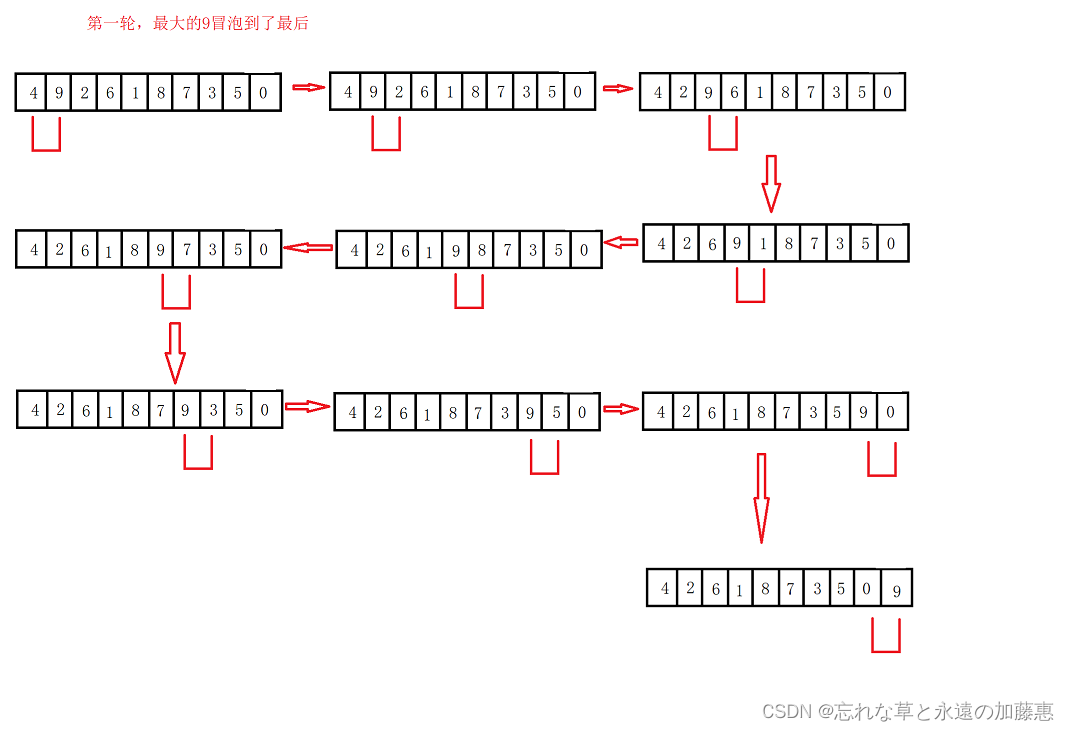
冒泡排序的逻辑就是每遍历一遍数组，把最大的数冒泡到最后，执行逻辑如下图所示，一前一后两个数比较，前面的数大于后面的数，二者就交换，最终使得最大的数到了最后面，然后这个数就不动了。然后在进行第二轮冒泡，倒数第二大的数冒泡到了倒数第二个位置，设一共有n个数，第一轮冒泡了n-1次，第二轮冒泡了n-2次......这样的话一共会执行n-1轮

?代码如下：

? ? ? ? 在这里有一个优化，就是在每一轮一遍创建一个变量isChange，记录这一轮里面是否有交换，如果有交换，isChange就变成了true，此时不会执行if里面的语句，如果本轮没有交换，表示这个数组已经是升序的了，也就是说不需要再执行后面的循环了，所以可以直接跳出循环

6. 快速排序

快速排序需要用到分治思想以及递归，有三种实现，方法，这三种方法的本质都是一样的，从数组中选出一个数，经过一种算法，使得最终选中的数左边的数都比它小，选中的数右边的数都比它大，但是此时它的左右两边并不是升序的，然后把这个数组分成三部分，假设这个选中的数下标是pivot，然后这三部分就是[left, pivot - 1], pivot, [pivot + 1, right]，然后将它的第一第三部分在进行这个算法，就是递归，最终就会循环

6.1 挖坑法

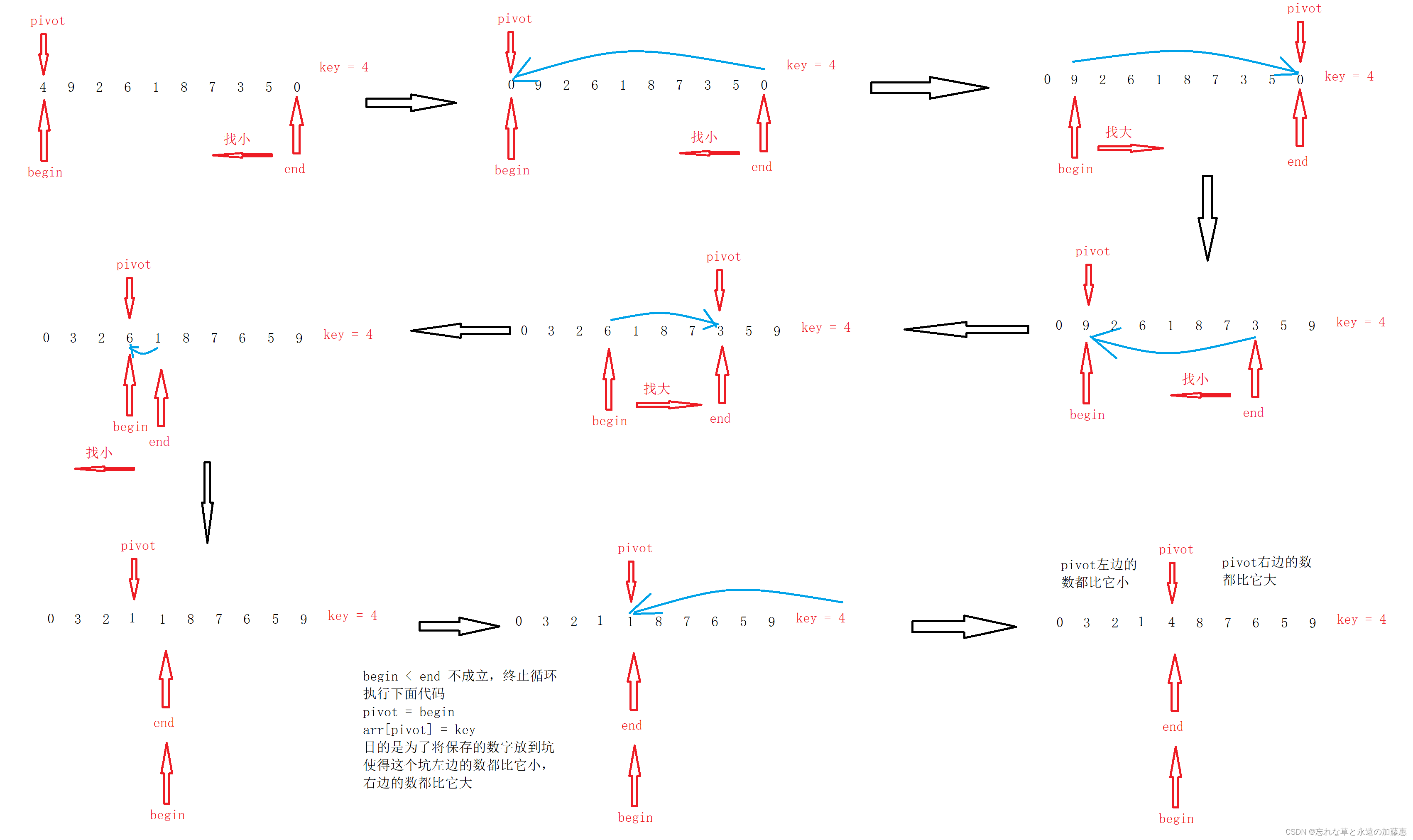
挖坑法顾名思义就是挖一个坑，然后往里面填数，步骤是这样的，用pivot记录数组中随便一个数的下标，这里用第一个数表示，然后用begin记录开始下标，end记录末尾下标，遍历开始，先是从end开始，从后往前遍历，直到找到一个数小于arr[pivot]，此时把end指向的位置的那个数放到坑位，然后end处自己变成坑，然后再从begin开始，找一个数是大于arr[pivot]的，找到了就把begin指向位置的数放到pivot处，然后begin指向的地方变成坑，直到begin>=end为止，最终，要执行两步代码，第一步是把pivot设置为begin，即 pivot = begin，然后把key保存的值放到pivot处，即 arr[pivot]? = key，遍历以后的结果就是pivot左边的数都比pivot指向的数小，pivot右边的数都比pivot指向的数大，此时可以把整个数组分成三部分，把第一部分和第三部分递归再执行这样的代码，直到他们有序。进入QuickSort函数中，如果left的值大于等于right的值，就返回

具体实现步骤可以看下面这幅图：

?具体实现代码如下：

// 快速排序
void QuickSort(int* arr, int left, int right){

  if(left >= right){
    return;
  }
  
  int begin = left, end = right;
  int pivot = begin;
  int key = arr[pivot];
  while(begin < end){
    // 右边找小
    while(begin < end && arr[end] >= key){
      end--;
    }
    // 把小的放到坑位，自己形成坑
    arr[pivot] = arr[end];
    pivot = end;

    // 左边找大
    while(begin < end && arr[begin] <= key){
      begin++;
    }
    // 把大的放到坑位，自己形成坑
    arr[pivot] = arr[begin];
    pivot = begin;
  }
  pivot = begin;
  arr[pivot] = key;

  // 此时数组被分成了 [begin, pivot - 1] pivot [pivot + 1, right]
  QuickSort(arr, left, pivot- 1);
  QuickSort(arr, pivot+ 1, right);
}

?但是对于这个代码还可以进行优化，那就是三数取中以及小区间优化

三数取中：就是从数组中下标为第一个、中间以及最后一个这三个数中取出中间大的，这是为了防止如果要排序的数组已经是有序的情况，时间复杂度会变成O(N^2)。把中间大的那个数和第一个数进行交换，然后在执行后续的代码。这三个取出的数也不一定就是要第一个、中间以及最后一个，只是大部分情况是这样而已。

小区间优化：比如说要排序的数有10W个，向下分割后如果分割的数组长度小于10，可以不再使用快排，而是使用直接插入排序，这样也会有性能提高，当然，分割后数组长度也不一定要10个才执行直接插入排序，还是要具体问题具体分析

下面这个快排的代码就是添加了三数取中以及小区间优化：

// 三数取中
int GetMidIndex(int* arr, int left, int right){
  int mid = (left + right) >> 1;
  if(arr[left] < arr[mid]){
    if(arr[mid] < arr[right]){
      return mid;
    }else if(arr[left] > arr[right]){
      return left;
    }else{
      return right;
    }
  }else{
    // arr[mid] <= arr[left]
    if(arr[left] < arr[right]){
      return left;
    }else if(arr[right] < arr[mid]){
      return mid;
    }else{
      return right;
    }
  }
}


// 快速排序——挖坑法
int PartSort(int* arr, int left, int right){

  int index = GetMidIndex(arr, left, right);
  swap(arr[left], arr[index]);
  
  int begin = left, end = right;
  int pivot = begin;
  int key = arr[pivot];
  while(begin < end){
    // 右边找小
    while(begin < end && arr[end] >= key){
      end--;
    }
    // 把小的放到坑位，自己形成坑
    arr[pivot] = arr[end];
    pivot = end;

    // 左边找大
    while(begin < end && arr[begin] <= key){
      begin++;
    }
    // 把大的放到坑位，自己形成坑
    arr[pivot] = arr[begin];
    pivot = begin;
  }
  pivot = begin;
  arr[pivot] = key;

  return pivot;
}

// 快速排序
void QuickSort(int* arr, int left, int right){

  if(left >= right){
    return;
  }
  
  int keyIndex = PartSort(arr, left, right);

  // 小区间优化
  if(keyIndex - 1 - left > 10){
    QuickSort(arr, left, keyIndex - 1);
  }else{
    InsertSort(arr + left, keyIndex - 1 - left + 1);
  }
  if(right - ( keyIndex + 1 ) > 10){
    QuickSort(arr, keyIndex + 1, right);
  }else{
    InsertSort(arr + keyIndex + 1, right - ( keyIndex + 1 ) + 1);
  }
}

6.2 前后指针法

前后指针法执行的逻辑：创建一个变量keyi始终指向第一个数，创建变量begin和end分别指向第一个数和最后一个数，先从end开始，从后往前遍历查找一个数，使得这个数小于arr[keyi]，在从begin开始，往后遍历，查找一个数，这个数要大于arr[keyi]，随后将begin和end指向的两个数交换，重复这个步骤，直到不满足begin < end 为止。此时还需要将begin和keyi指向的两个数交换，结果就是begin左边的数都比它小，begin右边的数都比它大，跟挖坑法大同小异，都是让一个数插入中间，左边小于它，右边大于他。然后也是要进行递归，直到排序完成。

?加上三数取中以及小区间优化的代码：

// 三数取中
int GetMidIndex(int* arr, int left, int right){
  int mid = (left + right) >> 1;
  if(arr[left] < arr[mid]){
    if(arr[mid] < arr[right]){
      return mid;
    }else if(arr[left] > arr[right]){
      return left;
    }else{
      return right;
    }
  }else{
    // arr[mid] <= arr[left]
    if(arr[left] < arr[right]){
      return left;
    }else if(arr[right] < arr[mid]){
      return mid;
    }else{
      return right;
    }
  }
}


// 快速排序——左右指针法
int PartSort(int* arr,int left, int right){

  int index = GetMidIndex(arr, left, right);
  swap(arr[left], arr[index]);

  int begin = left, end = right;
  int keyi = begin;

  while(begin < end){
    while(begin < end && arr[end] >= arr[keyi]){
      end--;
    }
    while(begin < end && arr[begin] <= arr[keyi]){
      begin++;
    }
    swap(arr[begin], arr[end]);
  }
  swap(arr[keyi], arr[begin]);

  return begin;
}

// 快速排序
void QuickSort(int* arr, int left, int right){

  if(left >= right){
    return;
  }
  
  int keyIndex = PartSort(arr, left, right);


  // 小区间优化
  if(keyIndex - 1 - left > 10){
    QuickSort(arr, left, keyIndex - 1);
  }else{
    InsertSort(arr + left, keyIndex - 1 - left + 1);
  }
  if(right - ( keyIndex + 1 ) > 10){
    QuickSort(arr, keyIndex + 1, right);
  }else{
    InsertSort(arr + keyIndex + 1, right - ( keyIndex + 1 ) + 1);
  }
}

6.3 前后指针法

前后指针法执行的逻辑是：创建变量keyi始终指向第一个数字，创建变量prev指向第一个数字，变量cur指向prev后面一个数，从cur开始往后遍历，如果遍历的数字满足arr[cur] < arr[keyi]，那么就让prev++，然后再让prev和cur指向的数字交换，不管满不满足这个条件，都要让cur往后移一位，直到cur < right这个条件不满足为止，最终还要将keyi上的数字和prev上的数字交换

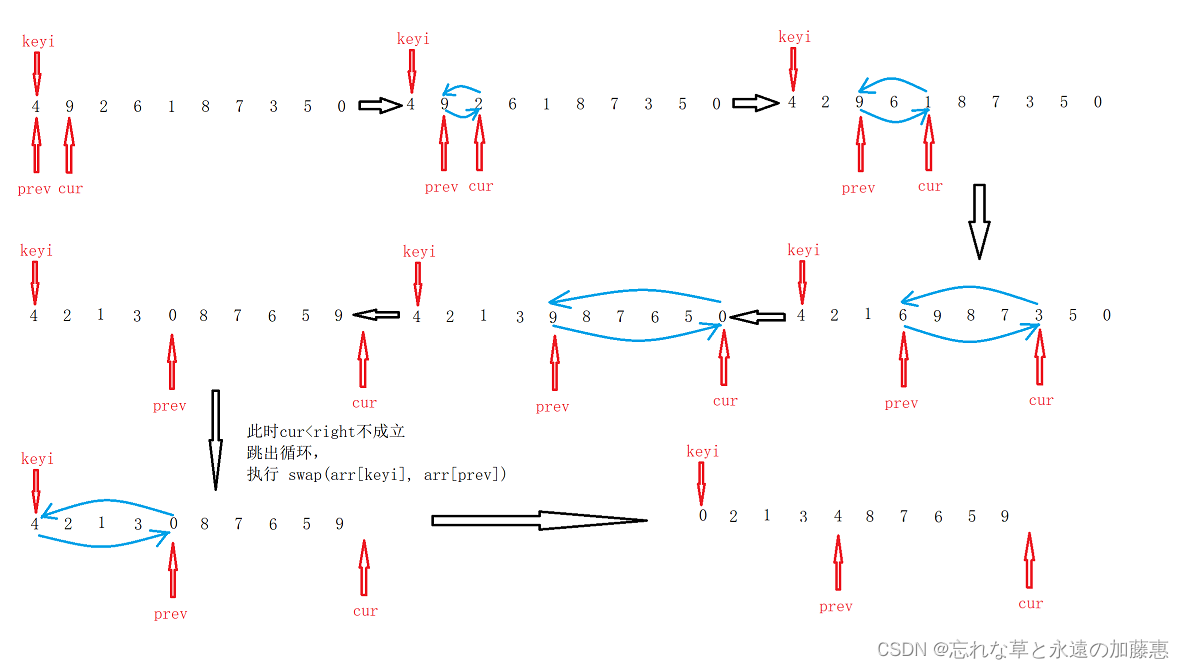
??加上三数取中以及小区间优化的代码：

// 三数取中
int GetMidIndex(int* arr, int left, int right){
  int mid = (left + right) >> 1;
  if(arr[left] < arr[mid]){
    if(arr[mid] < arr[right]){
      return mid;
    }else if(arr[left] > arr[right]){
      return left;
    }else{
      return right;
    }
  }else{
    // arr[mid] <= arr[left]
    if(arr[left] < arr[right]){
      return left;
    }else if(arr[right] < arr[mid]){
      return mid;
    }else{
      return right;
    }
  }
}

// 快速排序——前后指针法
int PartSort(int* arr, int left, int right){

  int index = GetMidIndex(arr, left, right);
  swap(arr[left], arr[index]);

  int keyi = left;
  int prev = left;
  int cur = prev + 1;
  while(cur <= right){
    // if(arr[cur] < arr[keyi]){
    //   prev++;
    //   swap(arr[prev], arr[cur]);
    // }
    if(arr[cur] < arr[keyi] && ++prev != cur){
      swap(arr[prev], arr[cur]);
    }
    cur++;
  }
  swap(arr[keyi], arr[prev]);

  return prev;
}

// 快速排序
void QuickSort(int* arr, int left, int right){

  if(left >= right){
    return;
  }
  
  int keyIndex = PartSort(arr, left, right);

  // 小区间优化
  if(keyIndex - 1 - left > 10){
    QuickSort(arr, left, keyIndex - 1);
  }else{
    InsertSort(arr + left, keyIndex - 1 - left + 1);
  }
  if(right - ( keyIndex + 1 ) > 10){
    QuickSort(arr, keyIndex + 1, right);
  }else{
    InsertSort(arr + keyIndex + 1, right - ( keyIndex + 1 ) + 1);
  }
}

7. 归并排序

归并排序就是把一个数组分成多个小的数组，让这些小的数组都变有序，然后再把这些小的数组合并起来

具体的实现步骤：

创建left指向第一个下标，right指向最后一个下标，mid指向中间的下标，也就是(left + right) / 2，然后把数组分成[left, mid]和[left + 1, right]，然后让这两个小的数组在进行这个步骤，直到left >= right，此时直接return。
创建一个新的数组tmp，大小和原数组一样大，将这两个小的数组分别从小到大遍历，用begin1指向第一个数组的第一个下标，end1指向最后一个下标，用begin2指向第二个数组的第一个下标，end2指向最后一个下标，创建index指向tmp数组的第一个下标，然后比较arr[begin1]和arr[begin2]，将小的那个数放到tmp中，比如说arr[begin1] < arr[begin2]，此时执行 tmp[index++] = arr[begin1++]，直到有一个小数组中的数字已经遍历完成，然后将没有遍历完的数组后面的数组都赋值到tmp中，具体见代码，如下是图示：

?代码：

void _MergeSort(int* arr, int left, int right, int* tmp){
  if(left >= right){
    return;
  }

  int mid = (left + right) >> 1;

  _MergeSort(arr, left, mid, tmp);
  _MergeSort(arr, mid + 1, right, tmp);

  int begin1 = left, end1 = mid;
  int begin2 = mid + 1, end2 = right;
  int index = left;

  while(begin1 <= end1 && begin2 <= end2){
    if(arr[begin1] < arr[begin2]){
      tmp[index++] = arr[begin1++];
    }else{
      tmp[index++] = arr[begin2++];
    }
  }

  while(begin1 <= end1){
    tmp[index++] = arr[begin1++];
  }
  while(begin2 <= end2){
    tmp[index++] = arr[begin2++];
  }

  for(int i = left; i <= right; i++){
    arr[i] = tmp[i];
  }
}

// 归并排序
void MergeSort(int* arr, int n){
  int* tmp = (int*)malloc(sizeof(int) * n);

  _MergeSort(arr, 0, n, tmp);

  free(tmp);
}

8. 快速排序（非递归）

先讲一下递归的缺陷吧，递归在某些极端的情况下可能导致栈帧深度太深，栈空间可能不够，会溢出

非递归改递归有两种办法：

直接改循环，这个是比较简单的情况
借助数据结构栈模拟递归，这个适用于复杂一点的情况

这里使用栈来实现快排的非递归，操作很简单，先把数组的最后一个下标和第一个下标存储到栈中，然后设置循环，直到栈空为止退出循环，取出栈最上面的两个下标，然后可以使用挖坑法、左右指针法、前后指针法来实现排序，返回一个下标keyIndex，此时把数组分成三部分[left, keyIndex - 1], keyIndex, [keyIndex + 1, right]，先把keyIndex + 1 和 right放进栈中，然后再把left 和 keyIndex - 1 放到栈中，但是如果不满足keyIndex + 1 < right 或者 left < keyIndex - 1 就不存储到栈中，把这些操作循环，直到栈为空，此时已经排序完成。

实现以及测试的代码如下：

// 三数取中
int GetMidIndex(int* arr, int left, int right){
  int mid = (left + right) >> 2;
  if(arr[left] < arr[mid]){
    if(arr[mid] < arr[right]){
      return mid;
    }else if(arr[left] > arr[right]){
      return left;
    }else{
      return right;
    }
  }else{
    // arr[mid] <= arr[left]
    if(arr[left] < arr[right]){
      return left;
    }else if(arr[right] < arr[mid]){
      return mid;
    }else{
      return right;
    }
  }
}

int PartSort1(int* arr, int left, int right){

  int index = GetMidIndex(arr, left, right);
  swap(arr[left], arr[index]);
  
  int begin = left, end = right;
  int pivot = begin;
  int key = arr[pivot];
  while(begin < end){
    // 右边找小
    while(begin < end && arr[end] >= key){
      end--;
    }
    // 把小的放到坑位，自己形成坑
    arr[pivot] = arr[end];
    pivot = end;

    // 左边找大
    while(begin < end && arr[begin] <= key){
      begin++;
    }
    // 把大的放到坑位，自己形成坑
    arr[pivot] = arr[begin];
    pivot = begin;
  }
  pivot = begin;
  arr[pivot] = key;

  return pivot;
}

// 快速排序非递归
void QuickSortNonR(int* arr, int n){
  stack<int> stk;

  stk.push(n - 1);
  stk.push(0);

  while(!stk.empty()){
    int left = stk.top();
    stk.pop();

    int right = stk.top();
    stk.pop();

    int keyIndex = PartSort1(arr, left, right);

    // 此时区间分成三部分 [left, keyIndex - 1] keyIndex [keyIndex + 1, right]
    if(right > keyIndex + 1){
      stk.push(right);
      stk.push(keyIndex + 1);
    }
    if(keyIndex - 1 > left){
      stk.push(keyIndex - 1);
      stk.push(left);
    }
  }
}

void TestQuickNonR(){
  int arr[] = { 4, 9, 2, 6, 1, 8, 7, 3, 5, 0 };
  QuickSortNonR(arr, sizeof(arr) / sizeof(int));
  PrintArray(arr, sizeof(arr) / sizeof(int));
}

9. 归并排序（非递归）

使用非递归的归并排序逻辑很简单，但是代码有一些是要注意的

逻辑：先让数组每两个数为一组，将他们排有序后赋值回原数组，然后再以4个数为一组，排有序后赋值回原数组，一次类推，最终就会排有序了，过程如下图所示：

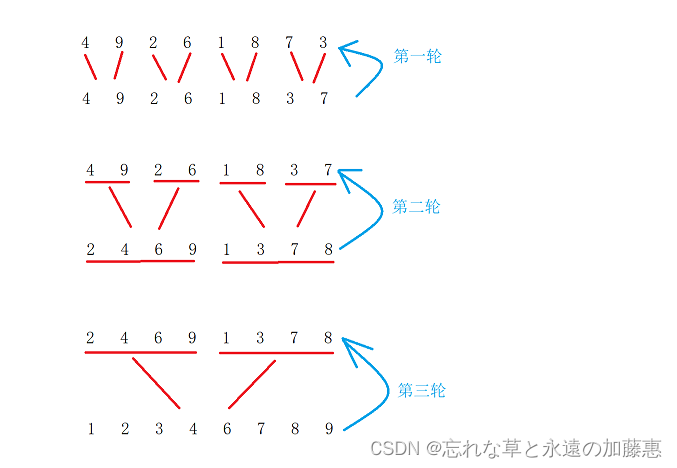
但是上面这个例子是个比较特别的，因为它的长度刚好不会出现越界的问题，那么如果数组长度不为8会怎么样的？

比如说数组长度为9，第一次遍历每两个数为一组，那么第九个数会怎么样呢？回答是直接跳出循环，因为是创建一个新数组的，即使没有重新赋值回去原数组也还是不会变。

第二个问题：如果第二个数组长度不够怎么办，比如说一共有11个数组，每四个数字为一组，那么第四组只有三个数，此时只需要修正右边界即可。

具体可见代码：

// 归并排序非递归
void MergeSortNonR(int* arr, int n){
  int* tmp = (int*)malloc(sizeof(int) * n);
  int gap = 1;
  while(gap < n){
    for(int i = 0; i < n; i += 2 * gap){
      // [i, i + gap - 1] [i + gap, i + 2 * gap - 1]
      int begin1 = i, end1 = i + gap - 1;
      int begin2 = i + gap, end2 = i + 2 * gap - 1;
      int index = i;

      // 如果第二组已经越界，则跳出循环
      if(begin2 >= n){
        break;
      }

      // 如果第二组长度不够，修正右边界
      if(end2 >= n){
        end2 = n - 1;
      }

      while(begin1 <= end1 && begin2 <= end2){
        if(arr[begin1] < arr[begin2]){
          tmp[index++] = arr[begin1++];
        }else{
          tmp[index++] = arr[begin2++];
        }
      }

      while(begin1 <= end1){
        tmp[index++] = arr[begin1++];
      }
      while(begin2 <= end2){
        tmp[index++] = arr[begin2++];
      }

      for(int j = i; j <= end2; j++){
        arr[j] = tmp[j];
      }
    }
    gap *= 2;
  }
  
}
void TestMergeSortNonR(){
  int arr[] = { 4, 9, 2, 6, 1, 8, 7, 3, 5, 0};
  MergeSortNonR(arr, sizeof(arr) / sizeof(int));
  PrintArray(arr, sizeof(arr) / sizeof(int));
}

10. 排序算法的比较

排序算法	平均情况	最好情况	最坏情况	辅助空间	稳定性
冒泡排序	O(n^2)	O(n)	O(n^2)	O(1)	稳定
选择排序	O(n^2)	O(n^2)	O(n^2)	O(1)	不稳定
插入排序	O(n^2)	O(n)	O(n^2)	O(1)	稳定
希尔排序	O(nlog n) ~ O(n^2)	O(n^1.3)	O(n^2)	O(1)	不稳定
堆排序	O(n log n)	O(n log n)	O(n log n)	O(1)	不稳定
归并排序	O(n log n)	O(n log n)	O(n log n)	O(n)	稳定
快速排序	O(n log n)	O(n log n)	O(n^2)	O(logn)~O(n)	不稳定

注意：快速排序加了三数取中选出key基本不会出现最坏情况

稳定性：假定在特排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i] = r[j]，且r[i] 在 r[j] 之前，而在排序后的序列中，r[i] 仍在 r[j] 之前，则称这种排序算法是稳定的，否知称为不稳定的。简单的讲，比如说A和B考试都考了100分，但是A比B先交卷，所以A应该排名在B前，所以在排序后A排名在B前面就是稳定的，否则是不稳定的。