[数据结构与算法]常用排序算法的实现（Java版）

常用排序算法

一、选择排序

选择排序是一种简单直观的排序算法

• 1、首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。
• 2、再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
• 3、重复第二步，直到所有元素均排序完毕。

动画演示

代码实现

/**
 * @author java小豪
 * @date 2022/6/1
 */
public class Code003SelectionSort {

    public static void swap(int[] arr, int i, int j) {
        int temp = arr[j];
        arr[j] = arr[i];
        arr[i] = temp;
    }

    public static void print(int[] nums) {
        for (int num : nums) {
            System.out.print(num + " ");
        }
        System.out.println();
    }

    public static void selectSort(int[] nums) {
        if (nums == null || nums.length < 2) {
            return;
        } 
        int len = nums.length;
        for (int i = 0; i < len; i++) {
            int minValueIndex = i;
            for (int j = i + 1; j < len; j++) {
                minValueIndex = nums[j] < nums[minValueIndex] ? j : minValueIndex;
            }
            swap(nums, i, minValueIndex);
        }
    }

    public static void bubbleSort(int[] nums) {
        if (nums == null || nums.length < 2) {
            return;
        }
        int len = nums.length;
        for (int end = len - 1; end >=0; end--) {
            for (int second = 1; second <= end; second++){
                if (nums[second - 1] > nums[second]) {
                    swap(nums, second - 1, second);
                }
            }
        }
    }



    public static void main(String[] args) {
        int[] arr = {6, 5, 8, 9, 7, 3, 1, 2, 4};
        print(arr);
        selectSort(arr);
        print(arr);
        bubbleSort(arr);
        print(arr);
    }
}

• 性质：
  • 1、时间复杂度：O(n2)
  • 2、空间复杂度：O(1)
  • 3、非稳定排序
  • 4、原地排序

二、冒泡排序

冒泡排序（Bubble Sort）也是一种简单直观的排序算法。

• 1、比较相邻的元素。如果第一个比第二个大，就交换他们两个。
• 2、对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
• 3、针对所有的元素重复以上的步骤，除了最后一个。
• 4、持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

动画演示

代码实现

/**
 * @author java小豪
 * @date 2022/6/1
 */
public class Code004BubbleSort {

    public static void swap(int[] arr, int i, int j) {
        int temp = arr[j];
        arr[j] = arr[i];
        arr[i] = temp;
    }

    public static void print(int[] nums) {
        for (int num : nums) {
            System.out.print(num + " ");
        }
        System.out.println();
    }
    public static void bubbleSort(int[] nums) {
        if (nums == null || nums.length < 2) {
            return;
        }
        int len = nums.length;
        for (int end = len - 1; end >=0; end--) {
            for (int second = 1; second <= end; second++){
                if (nums[second - 1] > nums[second]) {
                    swap(nums, second - 1, second);
                }
            }
        }
    }

    public static void main(String[] args) {
        int[] arr = {6, 5, 8, 9, 7, 3, 1, 2, 4};
        print(arr);
        bubbleSort(arr);
        print(arr);
    }
}

• 性质：
  1、 时间复杂度：O(n2)
  2、 空间复杂度：O(1)
  3、 稳定排序
  4、 原地排序

三、插入排序

当我们给无序数组做排序的时候，为了要插入元素，我们需要腾出空间，将其余所有元素在插入之前都向右移动一位，这种算法我们称之为插入排序。

• 1、将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。
• 2、从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）
  动画演示
  
  代码实现

/**
 * @author java小豪
 * @date 2022/6/1
 */
public class Code005InsertSort {
    public static void swap(int[] arr, int i, int j) {
        int temp = arr[j];
        arr[j] = arr[i];
        arr[i] = temp;
    }

    public static void print(int[] nums) {
        for (int num : nums) {
            System.out.print(num + " ");
        }
        System.out.println();
    }
    public static void insertSort1(int[] nums) {
        if (nums == null || nums.length < 2) {
            return;
        }
        int len = nums.length;
        for (int end = 1; end < len; end++) {
            int curNumIndex = end;
            while (curNumIndex - 1 >= 0 && nums[curNumIndex - 1] > nums[curNumIndex]) {
                swap(nums, curNumIndex - 1, curNumIndex);
                curNumIndex--;
            }
        }
    }

    /**
     * 优化的插入排序
     * @param nums 数组
     */
    public static void insertSort2(int[] nums) {
        if (nums == null || nums.length < 2) {
            return;
        }
        int len = nums.length;
        for (int end = 1; end < len; end++) {
            for (int pre = end - 1; pre >= 0 && nums[pre] > nums[end]; pre--) {
                swap(nums, pre, pre + 1);
            }

        }
    }

    public static void main(String[] args) {
        int[] arr = {6, 5, 8, 9, 7, 3, 1, 2, 4};
        print(arr);
        insertSort1(arr);
        print(arr);
        insertSort2(arr);
        print(arr);
    }
}

四、快速排序

快速排序使用分治法（Divide and conquer）策略来把一个串行（list）分为两个子串行（sub-lists）。
快速排序又是一种分而治之思想在排序算法上的典型应用。本质上来看，快速排序应该算是在冒泡排序基础上的递归分治法。

1. 从数列中挑出一个元素，称为 “基准”（pivot）;
2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；

动画演示

代码实现

public static int[] quickSort(int[] arr, int left, int right) {
        if (left < right) {
            //获取中轴元素所处的位置
            int mid = partition(arr, left, right);
            //进行分割
            arr = quickSort(arr, left, mid - 1);
            arr = quickSort(arr, mid + 1, right);
        }
        return arr;
    }

    private static int partition(int[] arr, int left, int right) {
        //选取中轴元素
        int pivot = arr[left];
        int i = left + 1;
        int j = right;
        while (true) {
            // 向右找到第一个大于等于 pivot 的元素位置
            while (i <= j && arr[i] <= pivot) {
                i++;
            }
            // 向左找到第一个小于等于 pivot 的元素位置
            while(i <= j && arr[j] >= pivot ) {
                j--;
            }
            if(i >= j) {
                break;
            }
            //交换两个元素的位置，使得左边的元素不大于pivot,右边的不小于pivot
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
        arr[left] = arr[j];
        // 使中轴元素处于有序的位置
        arr[j] = pivot;
        return j;
}

性质：

1. 时间复杂度：O(nlogn)
2. 空间复杂度：O(logn)
3. 非稳定排序
4. 原地排序

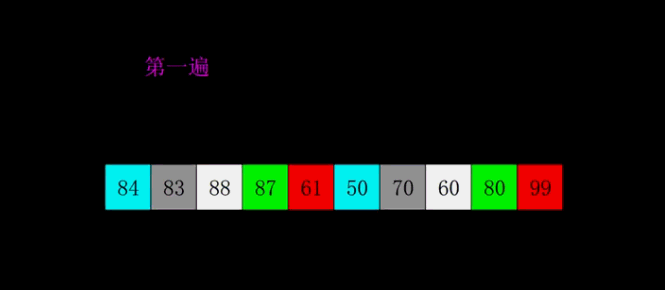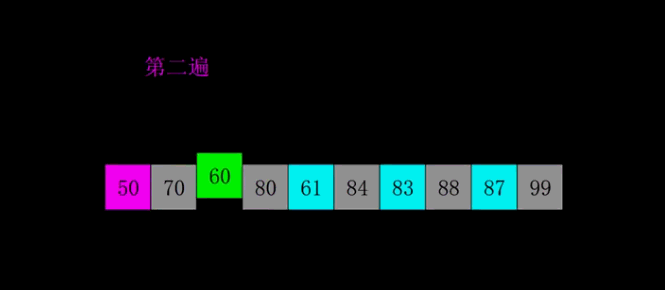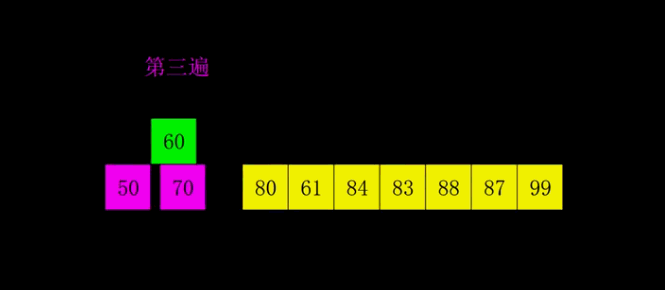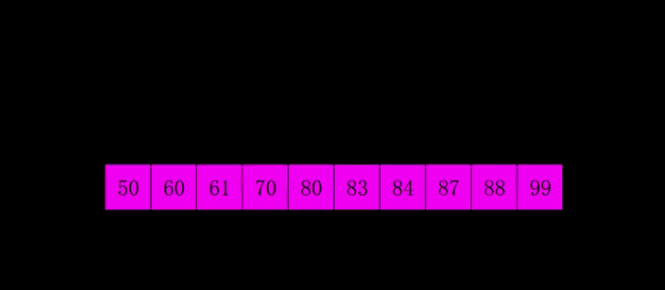
五、希尔排序

希尔排序，也称递减增量排序算法，是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，具体算法描述：

1. 选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；
2. 按增量序列个数k，对序列进行k 趟排序；
3. 每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

动画演示

代码实现

public class ShellSort {
    public static int[] shellSort(int arr[]) {
        if (arr == null || arr.length < 2) return arr;
        int n = arr.length;
        // 对每组间隔为 h的分组进行排序，刚开始 h = n / 2;
        for (int h = n / 2; h > 0; h /= 2) {
            //对各个局部分组进行插入排序
            for (int i = h; i < n; i++) {
                // 将arr[i] 插入到所在分组的正确位置上
                insertI(arr, h, i);
            }
     }
     return arr;
    }

    /**
     * 将arr[i]插入到所在分组的正确位置上
     * arr[i]] 所在的分组为 ... arr[i-2*h],arr[i-h], arr[i+h] ...
     */
    private static void insertI(int[] arr, int h, int i) {
        int temp = arr[i];
        int k;
        for (k = i - h; k >= 0 && temp < arr[k]; k -= h) {
            arr[k + h] = arr[k];
        }
        arr[k + h] = temp;
    }
}

六、归并排序

归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置；
3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；
4. 重复步骤 3 直到某一指针达到序列尾；
5. 将另一序列剩下的所有元素直接复制到合并序列尾。

动画演示

代码实现

public class Code007MergeSort {
    // 归并排序
    public static int[] mergeSort(int[] arr, int left, int right) {
        // 如果 left == right，表示数组只有一个元素，则不用递归排序
        if (left < right) {
            // 把大的数组分隔成两个数组
            int mid = left + (right - left) / 2;
            // 对左半部分进行排序
            arr = mergeSort(arr, left, mid);
            // 对右半部分进行排序
            arr = mergeSort(arr, mid + 1, right);
            //进行合并
            merge(arr, left, mid, right);
        }
        return arr;
    }

    // 合并函数，把两个有序的数组合并起来
    // arr[left..mif]表示一个数组，arr[mid+1 .. right]表示一个数组
    private static void merge(int[] arr, int left, int mid, int right) {
        //先用一个临时数组把他们合并汇总起来
        int[] a = new int[right - left + 1];
        int i = left;
        int j = mid + 1;
        int k = 0;
        while (i <= mid && j <= right) {
            if (arr[i] < arr[j]) {
                a[k++] = arr[i++];
            } else {
                a[k++] = arr[j++];
            }
        }
        while(i <= mid) a[k++] = arr[i++];
        while(j <= right) a[k++] = arr[j++];
        // 把临时数组复制到原数组
        for (i = 0; i < k; i++) {
            arr[left++] = a[i];
        }
    }
}

非递归：

public class Code008MergeSort {
    // 非递归式的归并排序
    public static int[] mergeSort(int[] arr) {
        int n = arr.length;
        // 子数组的大小分别为1，2，4，8...
        // 刚开始合并的数组大小是1，接着是2，接着4....
        for (int i = 1; i < n; i += i) {
            //进行数组进行划分
            int left = 0;
            int mid = left + i - 1;
            int right = mid + i;
            //进行合并，对数组大小为 i 的数组进行两两合并
            while (right < n) {
                // 合并函数和递归式的合并函数一样
                merge(arr, left, mid, right);
                left = right + 1;
                mid = left + i - 1;
                right = mid + i;
            }
            // 还有一些被遗漏的数组没合并，千万别忘了
            // 因为不可能每个字数组的大小都刚好为 i
            if (left < n && mid < n) {
                merge(arr, left, mid, n - 1);
            }
        }
        return arr;
    }
}

性质：

• 1、时间复杂度：O(nlogn)
• 2、空间复杂度：O(n)
• 3、稳定排序
• 4、非原地排序