一【题目类别】

动态规划

二【题目难度】

困难

三【题目编号】

42.接雨水

四【题目描述】

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

五【题目示例】

示例 1：
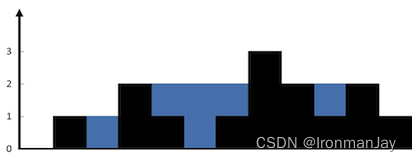
- 输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
- 输出：6
- 解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。
示例 2：
- 输入：height = [4,2,0,3,2,5]
- 输出：9

六【解题思路】

利用动态规划的思想
首先确定接雨水的计算方式，用列去计算比较方便，因为底固定为1，只需确定高即可
那么当前列可以接雨水的体积就是：min(当前列左边的最高值，当前列右边的最高值) - 当前列高度即可
确定了计算方法之后我们只需要分别求得某列左边和右边的最大高度
某列左边的最大高度的动态方程为：dpLeft[i] = max(dpLeft[i - 1], height[i])
某列右边的最大高度的动态方程为：dpRight[i] = max(dpRight[i + 1], height[i])
最后再遍历一遍数组就可以根据动态方程和体积公式求出所有可以接到水的最大体积
最后返回结果即可

七【题目提示】

$n == h e i g h t . l e n g t h$
$1 <= n <= 2 * 10^4$
$0 <= height[i] <= 10^5$

八【时间频度】

时间复杂度： $O (n)$ ，其中 $n$ 是数组长度
空间复杂度： $O (n)$ ，其中 $n$ 是数组长度

九【代码实现】

Java语言版

package DynamicProgramming;

public class p42_TrappingRainWater {

    public static void main(String[] args) {
        int[] height = {0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1};
        int res = trap(height);
        System.out.println("res = " + res);
    }

    public static int trap(int[] height) {
        int len = height.length;
        int[] dpLeft = new int[len];
        dpLeft[0] = height[0];
        int[] dpRight = new int[len];
        dpRight[len - 1] = height[len - 1];
        int water = 0;
        for (int i = 1; i < len; i++) {
            dpLeft[i] = Math.max(dpLeft[i - 1], height[i]);
        }
        for (int i = len - 2; i >= 0; i--) {
            dpRight[i] = Math.max(dpRight[i + 1], height[i]);
        }

        for (int i = 1; i <= len - 1; i++) {
            int level = Math.min(dpLeft[i], dpRight[i]);
            water += Math.max(0, level - height[i]);
        }
        return water;
    }

}

C语言版

#include<stdio.h>
#include<stdlib.h>

#define max(a,b) ((a) > (b) ? (a) : (b))
#define min(a,b) ((a) > (b) ? (b) : (a))

int trap(int* height, int heightSize)
{
	int* dpLeft = (int*)malloc(sizeof(int) * heightSize);
	dpLeft[0] = height[0];
	int* dpRight = (int*)malloc(sizeof(int) * heightSize);
	dpRight[heightSize - 1] = height[heightSize - 1];
	int water = 0;
	for (int i = 1; i < heightSize; i++)
	{
		dpLeft[i] = max(dpLeft[i - 1], height[i]);
	}
	for (int i = heightSize - 2; i >= 0; i--)
	{
		dpRight[i] = max(dpRight[i + 1], height[i]);
	}
	for (int i = 1; i < heightSize - 1; i++)
	{
		int level = min(dpLeft[i], dpRight[i]);
		water += max(0, level - height[i]);
	}
	return water;
}

/*主函数省略*/