链表结构
一、存储方式的分类
(一)顺序存储结构
在（子）程序的说明部分就必须加以说明，以便分配固定大小的存储单元，直到（子） 程序结束，才释放空间。
因此，这种存储方式又称为静态存储，所定义的变量称为静态变量。
它的优缺点如下：
- 优点：可以通过一个简单的公式随机存取表中的任一元素，逻辑关系上相邻的两个元素在物理位置上也是相邻的，且很容易找到前趋与后继元素。
- 缺点：在线性表的长度不确定时，必须分配最大存储空间，使存储空间得不到充分利用，浪费了宝贵的存储资源；线性表的容量一经定义就难以扩充；在插入和删除线性表的元素时，需要移动大量的元素，浪费了时间。
(二)链式存储结构
在程序的执行过程中，通过两个命令向计算机随时申请存储空间或随时释放存储空间， 以达到动态管理、使用计算机的存储空间，保证存储资源的充分利用。这样的存储方式称为动态存储，所定义的变量称为动态变量。
它的优点如下：
- 可以用一组任意的存储单元（这些存储单元可以是连续的，也可以不连续的）存储线性表的数据元素，这样就可以充分利用存储器的零碎空间。
二、 数组与链表
(一)链表的概念
链表是一种物理存储结构上非连续，非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。
链表的结构是多式多样的，通常用的也就是两种：
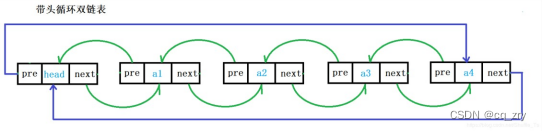
无头单向非循环列表： 结构简单，一般不会单独用来存放数据。
实际中更多是作为其他数据结构的子结构，比如说哈希桶等。
带头双向循环链表： 结构最复杂，一般单独存储数据。实际中经常使用的链表数据结构， 都是带头双向循环链表。
这个结构虽然复杂，但是使用代码实现后会发现这个结构会带来很多优势，实现反而简单了。
(二)链表和数组的区别
- 数组静态分配内存，链表动态分配内存。
- 数组在内存中是连续的，链表是不连续的。
- 数组利用下标定位，查找的时间复杂度是 O ( 1 ) O(1) O(1)，链表通过遍历定位元素，查找的时间复杂度是 O ( N ) O(N) O(N)。
- 数组插入和删除需要移动其他元素，时间复杂度是 O ( N ) O(N) O(N)，链表的插入或删除不需要移动其他元素，时间复杂度是 O ( 1 ) O(1) O(1)。
(三)数组的优点
- 随机访问性比较强，可以通过下标进行快速定位。
- 查找速度快。
(四)数组的缺点
- 插入和删除的效率低，需要移动其他元素。
- 会造成内存的浪费，因为内存是连续的，所以在申请数组的时候就必须规定其内存的大小，如果不合适，就会造成内存的浪费。
- 内存空间要求高，创建一个数组，必须要有足够的连续内存空间。
- 数组的大小是固定的，在创建数组的时候就已经规定好，不能动态拓展。
(五)链表的优点
- 插入和删除的效率高，只需要改变指针的指向就可以进行插入和删除。
- 内存利用率高，不会浪费内存，可以使用内存中细小的不连续的空间，只有在需要的时候才去创建空间。大小不固定，拓展很灵活。
(六)链表的缺点
查找的效率低，因为链表是从第一个节点向后遍历查找。
(七)单链表和双链表的区别
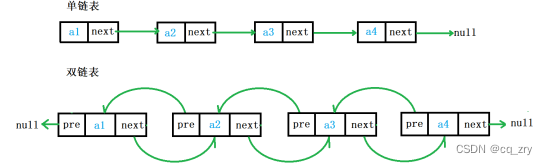单链表的每一个节点中只有指向下一个结点的指针，不能进行回溯，适用于节点的增加和删除。
双链表的每一个节点给中既有指向下一个结点的指针，也有指向上一个结点的指针，可以快速的找到当前节点的前一个节点，适用于需要双向查找节点值的情况。
(八)双链表相对于单链表的优点
删除单链表中的某个节点时，一定要得到待删除节点的前驱，得到其前驱的方法一般是在定位待删除节点的时候一路保存当前节点的前驱，这样指针总的移动操作为 2 n 2n 2n 次，如果是用双链表，就不需要去定位前驱，所以指针总的移动操作为 n n n 次。
查找时也是一样的，可以用二分法的思路，从头节点向后和尾节点向前同时进行，这样效率也可以提高一倍，但是为什么市场上对于单链表的使用要超过双链表呢？
从存储结构来看，每一个双链表的节点都比单链表的节点多一个指针，如果长度是 n， 就需要 n ? l e n g t h n*length n?length（32 位是 4 字节，64 位是 8 字节）的空间，这在一些追求时间效率不高的
应用下就不适用了，因为他占的空间大于单链表的 1 / 3 1/3 1/3，所以设计者就会用时间换空间。
(九)链表环问题
1.判断单链表是否有环
使用两个 slow, fast 指针从头开始扫描链表。指针 slow 每次走 1 步，指针 fast 每次走 2 步。如果存在环，则指针 slow、fast 会相遇；如果不存在环，指针 fast 遇到 NULL 退出。
就是所谓的追击相遇问题：
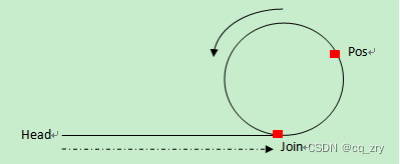
2.求有环单链表的环长
在环上相遇后，记录第一次相遇点为 Pos，之后指针 slow 继续每次走 1 步，fast 每次走2 步。在下次相遇的时候 fast 比 slow 正好又多走了一圈，也就是多走的距离等于环长。
设从第一次相遇到第二次相遇，设 slow 走了 len 步，则 fast 走了
2
?
l
e
n
2*len
2?len 步，相遇时多走了一圈：
环长=2*len-len
3.求有环单链表的环连接点位置
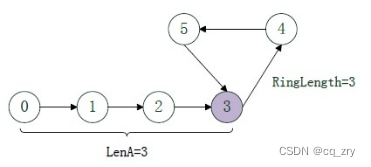
第一次碰撞点 Pos 到连接点 Join 的距离=头指针到连接点 Join 的距离，因此，分别从第一次碰撞点 Pos、头指针 head 开始走，相遇的那个点就是连接点。
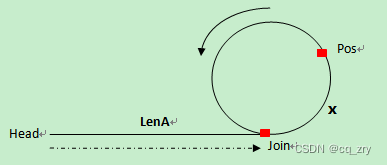
在环上相遇后，记录第一次相遇点为 Pos，连接点为 Join，假设头结点到连接点的长度为 L e n A LenA LenA，连接点到第一次相遇点的长度为 x x x，环长为 R R R。
第一次相遇时，slow 走的长度
S
=
L
e
n
A
+
x
;
S=LenA+x;
S=LenA+x;
第一次相遇时，fast 走的长度
2
S
=
L
e
n
A
+
n
?
R
+
x
;
2S=LenA+n*R+x;
2S=LenA+n?R+x;
所以可以知道，
L
e
n
A
+
x
=
n
?
R
;
L
e
n
A
=
n
?
R
?
x
;
LenA+x=n*R;LenA = n*R -x;
LenA+x=n?R;LenA=n?R?x;
4.求有环单链表的链表长
上述 2 中求出了环的长度；3 中求出了连接点的位置，就可以求出头结点到连接点的长度。两者相加就是链表的长度。
三、链表的实现与应用
(一)单链表的定义
1.类型和变量的说明
sturct node{
int data;
node *next;
};
node *p;
2.申请存储单元
(动态申请、空间大小由指针变量的基类型决定)
p=new node;
3.指针变量的赋值
指针变量名=NULL； //初始化，暂时不指向任何存储单元
如何表示和操作指针变量？
不同于简单变量（如A=0；），c++规定用“指针变量名->”的形式引用指针变量（如P->data=0；）。
(二）单链表的结构、建立、输出
由于单链表的每个结点都有一个数据域和一个指针域，所以，每个结点都可以定义成一个记录。下面给出建立并输出单链表的程序，大家可以把它改成过程用在以后的程序当中。
#include<bits/stdc++.h>
using namespace std;
struct Node{
int data;//数据域
Node *next;//指针域
};
Node *head,*p,*r;//head:头指针,p:临时指针,r:尾指针
int x;
int main()
{
cin>>x;
head=new Node;//申请头结点
r=head;
while(x!=-1)//读入的数不是-1
{
p=new Node;//申请一个新结点
p->data=x;
p->next=NULL;
r->next=p;//把新结点链接到前面的链表中，实际上r是p的直接前驱
r=p;//尾指针后移一个
cin>>x;
}
p=head->next;//头指针没有数据，只要从第一个结点开始就行了
while(p->next!=NULL)
{
cout<<p->data<<" ";
p=p->next;
}
cout<<p->data<<endl;//最后一个结点的数据单独输出
return 0;//也可以改成do-while循环
}
(三）单链表的操作
1.查找“数据域满足一定条件的结点”
p=head->next;
while((p->data!=x)&&(p->next!=NULL))
{
p=p->next;//找到第一个就结束
}
if(p->data==x)
{
//找到就处理
}
else
{
//输出不存在
}
如果想找到所有满足条件的结点，则修改如下：
p=head->next;
while(p->next!=NULL)//一个一个判断
{
if(p->data==x)
{
//找到一个处理一个
}
p=p->next;
}
2.取出单链表的第 i 个结点的数据域
void get(Node *head,int i)//取出单链表的第 i 个结点的数据域
{
Node *p;
p=head->next;
int j=1;
while((p!=NULL)&&(j<i))
{
p=p->next;
j++;
}
if((p!=NULL)&&(j==i))
{
cout<<p->data;
}
else
{
cout<<"i not exsit!";
}
}
3.插入一个结点在单链表中去
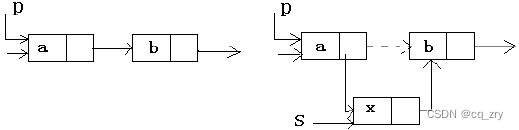
(插入结点前和后的链表变化)
void insert(Node *head,int i,int x)//插入x到第i个元素之前
{
Node *p,*s;
p=head;
int j=0;
while((p!=NULL)&&(j<i-1))
{//寻找第i-1个结点，插在它的后面
p=p->next;
j++;
}
if(p==NULL)
{
cout<<"no this position!";
}
else//插入
{
s=new Node;
s->data=x;
s->next=p->next;
p->next=s;
}
}
4.删除单链表中第i个结点
如图中的
b
b
b结点：
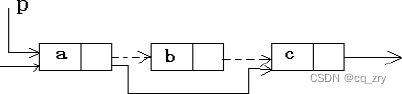
(删除一个结点前和后链表的变化)
void delet(Node *head,int i)//删除第i个元素
{
Node *p,*s;
p=head;
int j=0;
while((p->next!=NULL)&&(j<i-1))
{
p=p->next;
j++;
}//p指向第i-1个结点
if(p->next==NULL)
{
cout<<"no this position!";
}
else
{//删除p的后继结点，假设为s
s=p->next;
p->next=p->next->next;//同价于:p->next=s->next
free(s);
}
}
5.求单链表的实际长度
int len(Node *head)
{
int n=0;
p=head;
while(p!=NULL)
{
n++;
p=p->next;
}
return n;
}
（四）双向链表
每个结点有两个指针域和若干数据域，其中一个指针域指向它的前趋结点，一个指向它的后继结点。它的优点是访问、插入、删除更方便，速度也快了，“是以空间换时间”。
struct node{
int data;
node *pre,*next;//pre指向前驱，next指向后继
};
node *head,*p,*q,*r;
1.双向链表的插入
void insert2(node *head,int i,int x)//插入x到第i个元素之前
{
node *p,*s;
int j=0;
s=new node;
s->data=x;
p=head;
while((p->next!=NULL)&&(j<i))
{
p=p->next;
j++;
}//p指向第i个结点
if(p==NULL)
{
cout<<"no this position!";
}
else//将结点s插入到结点p之前
{
s->pre=p->pre;
p->pre->next=s;
s->next=p;
p->pre=s;
}
}
2.双向链表的删除
void delete2(node *head,int i)//删除双向链表的第i个结点
{
node *p;
p=head;
int j=0;
while((p->next!=NULL)&&(j<i))
{
p=p->next;
j++;
}//p指向第i个结点
if(p==NULL)
{
cout<<"no this position!";
}
else
{//将结点p删除
p->pre->next=p->next;
p->next->pre=p->pre;
}
}
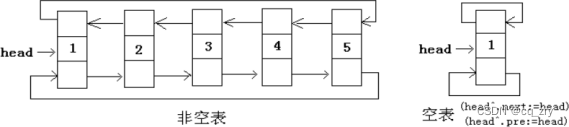
（五）循环链表
单向循环链表：最后一个结点的指针指向头结点。
（空表）
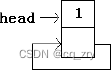
（非空表)
双向循环链表：最后一个结点的指针指向头结点，且头结点的前趋指向最后一个结点。
（六）循环链表的应用举
例 :约瑟夫环问题
题目描述
有 M M M个人，其编号分别为 1... M 1...M 1...M，这M个人按顺序排成一个圈。现在给定一个数 N N N，从第一个人开始依次报数，数到 N N N的人出列，然后又从下一个人开始又从1开始依次报数，数到 N N N的人又出列…如此循环，直到最后一个人出列为止。
输入格式
输入只有一行，包括2个整数 M ， N M，N M，N，之间用一个空格分开 ( 0 < n < = m < = 100 ) (0 < n <= m <= 100) (0<n<=m<=100)。
输出格式
输出只有一行，包括 M M M个整数
样列输入
8 5
样列输出
5 2 8 7 1 4 6 3
代码示例
#include<bits/stdc++.h>
using namespace std;
struct aa{
long d;
aa *next;
} *head,*p,*r;
long n,m;
int main()
{
cin>>n>>m;
head=new aa;
head->d=1;
head->next=NULL;
r=head;
for(int i=2;i<=n;i++)
{
p=new aa;
p->d=i;
p->next=NULL;
r->next=p;
r=p;
}
r->next=head;
r=head;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m-2;j++)
{
r=r->next;
}
cout<<r->next->d<<" ";
r->next=r->next->next;
r=r->next;
}
return 0;
}