1.栈
1.1栈的概念及结构

1.2栈的实现
void StackCheckCapacity(Stack* ps)
{
assert(ps);
if (ps->size == ps->capacity)
{
// realloc(地址,要申请的空间总的字节数)可以完成下述操作
// 1. 开辟新空间
int newCapacity = ps->capacity * 2;
DataType* temp = malloc(sizeof(DataType)*newCapacity);
if (NULL == temp)
{
assert(0);
printf("StackCheckCapacity:malloc失败!!!\n");
return;
}
// 2. 将旧空间中的元素拷贝到新空间
memcpy(temp, ps->array, sizeof(DataType)*ps->size);
// 3. 释放旧空间
free(ps->array);
// 4. 使用新空间
ps->array = temp;
ps->capacity = newCapacity;
}
}
// 入栈
void StackPush(Stack* ps, DataType data)
{
// 如果空间不够,需要库容
StackCheckCapacity(ps);
ps->array[ps->size] = data;
ps->size++;
}
// 出栈
void StackPop(Stack* ps)
{
if (StackEmpty(ps))
return;
ps->size--;
}
// 获取栈顶元素
DataType StackTop(Stack* ps)
{
assert(ps);
return ps->array[ps->size - 1];
}
// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
assert(ps);
return ps->size;
}
// 检测栈是否为空: 空返回真,否则返回假
int StackEmpty(Stack* ps)
{
assert(ps);
return 0 == ps->size;
}
// 栈的销毁操作
void StackDestroy(Stack* ps)
{
assert(ps);
free(ps->array);
ps->array = NULL;
ps->capacity = 0;
ps->size = 0;
}
1.3 经典练习题
1.一个栈的初始状态为空。现将元素1、2、3、4、5、A、B、C、D、E依次入栈,然后再依次出栈,则元素出 栈的顺序是(?b)。
栈的应用场景:利用它改变顺序
Leetcode 20 有效括号
给定一个只包括 '(',')','{','}','[',']'?的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号
来源:力扣(LeetCode)
?
思路:先对所有括号遍历,拿到每个括号ch
1.如果是左括号,入栈。
2.否则是右括号? 需要找对应的左括号来进行匹配,左括号都在栈中因此需要与栈顶的左括号进行匹配,获取栈顶的左括号top,? ch==(? && top== )? ? ? ? ? ? ch==[ && top==]?? ? ? ?ch={&&top==}
3.如果所有括号都匹配了,在循环结束之后,栈一定是空的
4.拿到右括号,需要和栈顶的左括号进行比对,此时要保证栈顶必须有左括号
单链表的逆序打印
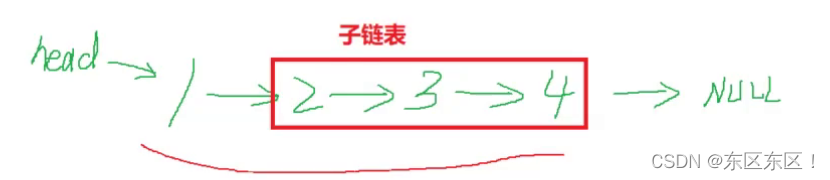
?
方法1:借助辅助空间给一个数组,遍历链表遇到每个节点时将值域存储到数组中,将数组从尾到头打印
方法2:采用递归(画个图就行)
void PrintListReverse(ListNode* head)
{
? ? ? if(head){
? ? ?PrintListReverse(head->next);
? ? ?printf("%d", head->next);
? ? ?}
}
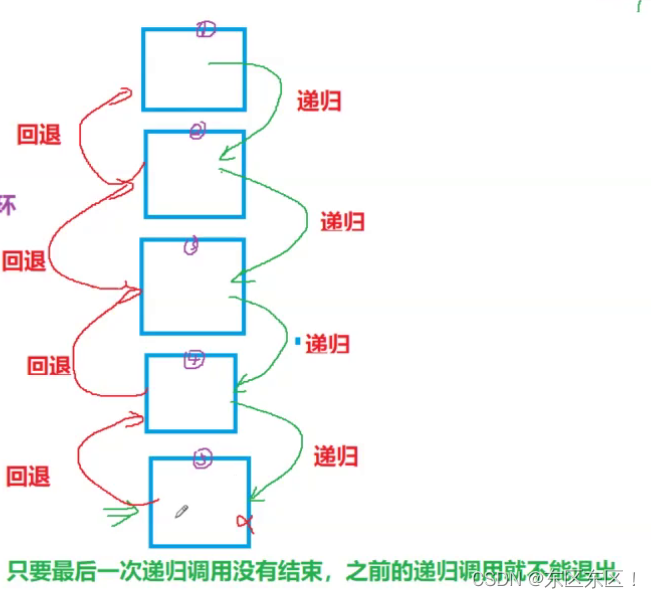
?
方法3:栈操作
将递归转换为循环(用栈操作)
void PrintListReverse(ListNode* head)
{
Stack s;
Stackinit(&s);
ListNode* cur =head;
while(cur)
{
StackPush(&s,cur->data);
cur = cur->next;
}
while(! StackEmpty(&s))
{
printf("%d", StackTop(&s));
StackPop(&s);
}
}1.4 堆栈、栈区、栈帧
堆栈:一般指的都是数据结构中,具有先进后出特性的数据结构、
栈区:程序运行起来后,操作系统给进程划分的虚拟地址空间中一块特殊的内存空间。(内部一般储存的都是调用时候需要存储的一些数据)
栈帧:每个函数在运行之前,操作系统负责给方法划分一块独立的栈空间,来组织该函数运行时需要存储的一些数据:形参、局部变量、语句中间运行结果、寄存器信息等


?
?