前言
本节介绍几个二叉树的题目,点击开始挑战!!!
一. 单值二叉树
1. 原题链接
2. 题目要求
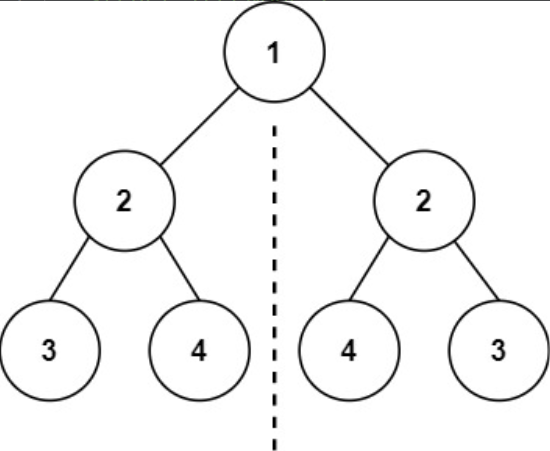
如果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树。
只有给定的树是单值二叉树时,才返回 t r u e true true;否则返回 f a l s e false false。
示例 1 1 1:
输入: [ 1 , 1 , 1 , 1 , 1 , n u l l , 1 ] [1,1,1,1,1,null,1] [1,1,1,1,1,null,1]
输出:4true$
示例 2 2 2:
输入: [ 2 , 2 , 2 , 5 , 2 ] [2,2,2,5,2] [2,2,2,5,2]
输出: f a l s e false false
提示:
给定树的节点数范围是 [ 1 , 100 ] [1, 100] [1,100]。
每个节点的值都是整数,范围为 [ 0 , 99 ] [0, 99] [0,99] 。
3. 基础框架
- C版本的代码框架
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
bool isUnivalTree(struct TreeNode* root){
}
4. 思路分析
(
1
)
(1)
(1)判断二叉树的所有节点是否全部相等,分治思想,分解为根和左右子树的问题。
(
2
)
(2)
(2)根首先进行判断,根和孩子节点(如果存在的话)储存的值有一个不相等就结束,返回
f
a
l
s
e
false
false;
(
3
)
(3)
(3)子树又分为根和左右子树,继续根和子树的值是否相等的判断。
(
4
)
(4)
(4)直到遇到空树就返回,返回结果是
t
r
u
e
true
true,因为空树不影响结果。
假设树的节点数为 N N N
时间复杂度 O ( N ) O(N) O(N)
空间复杂度 O ( N ) O(N) O(N)
5. 代码实现
bool isUnivalTree(struct TreeNode* root){
//分为根和子树
if(root == NULL){
return true;
}
//判断左孩子节点存在且根于左孩子节点所存的值相等
if(root->left && root->left->val != root->val){
return false;
}
//判断右孩子节点存在且根与右孩子节点所存的值相等
if(root->right && root->right->val != root->val){
return false;
}
//左右子树有一个子树不是单值就返回false
return isUnivalTree(root->left) && isUnivalTree(root->right);
}
二. 相同的树
1. 原题链接
2. 题目要求
给你两棵二叉树的根节点 p p p 和 q q q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
输入: p = [ 1 , 2 , 3 ] , q = [ 1 , 2 , 3 ] p = [1,2,3], q = [1,2,3] p=[1,2,3],q=[1,2,3]
输出:true
示例 2:
输入: p = [ 1 , 2 ] , q = [ 1 , n u l l , 2 ] p = [1,2], q = [1,null,2] p=[1,2],q=[1,null,2]
输出: f a l s e false false
示例 3:
输入: p = [ 1 , 2 , 1 ] , q = [ 1 , 1 , 2 ] p = [1,2,1], q = [1,1,2] p=[1,2,1],q=[1,1,2]
输出: f a l s e false false
提示:
两棵树上的节点数目都在范围 [ 0 , 100 ] [0, 100] [0,100] 内
? 104 < = N o d e . v a l < = 104 -104 <= Node.val <= 104 ?104<=Node.val<=104
3. 基础框架
- C版本的代码框架
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
}
4. 思路分析
(
1
)
(1)
(1)判断两树是否对应相等,先对两根进行判断:
(
2
)
(2)
(2)两根都为空说明都是空树,则相等;
(
3
)
(3)
(3)两根有一个为空,则一定不相等;
(
4
)
(4)
(4)两根都不为空,判断两根储存内容是否相等,不相等就直接返回;相等继续判断左右子树的情况。
时间复杂度 O ( N ) O(N) O(N)
空间复杂度 O ( N ) O(N) O(N)
5. 代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
//根节点都为空,返回真
if(p == NULL && q == NULL){
return true;
}
//有且只有一个根为空,则不相等,返回假
if(p == NULL || q == NULL){
return false;
}
//两根都不为空且不相等,返回假
if(p->val != q->val){
return false;
}
//到这里说明两根相等,接下来判断子树是否都对应相等
return isSameTree(p->left, q->left) &&
isSameTree(p->right, q->right);
}
三. 对称二叉树
1. 原题链接
2. 题目要求
给你一个二叉树的根节点 r o o t root root , 检查它是否轴对称。
示例 1:
输入: r o o t = [ 1 , 2 , 2 , 3 , 4 , 4 , 3 ] root = [1,2,2,3,4,4,3] root=[1,2,2,3,4,4,3]
输出: t r u e true true
示例 2:
输入: r o o t = [ 1 , 2 , 2 , n u l l , 3 , n u l l , 3 ] root = [1,2,2,null,3,null,3] root=[1,2,2,null,3,null,3]
输出: f a l s e false false
提示:
树中节点数目在范围
[
1
,
1000
]
[1, 1000]
[1,1000] 内
?
100
<
=
N
o
d
e
.
v
a
l
<
=
100
-100 <= Node.val <= 100
?100<=Node.val<=100
3. 基础框架
- C版本的代码框架
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
bool isSymmetric(struct TreeNode* root){
}
4. 思路分析
(
1
)
(1)
(1)判断一颗二叉树是否轴对称,等价于判断二叉树除根节点外的左子树、右子树是否轴对称,等价于判断两颗二叉树是否相等。
(
2
)
(2)
(2)也就是说,把给出的二叉树的除主根节点外的左子树看做一颗新的二叉树,把右子树看做另一颗新的二叉树。
(
3
)
(3)
(3)与判断两颗二叉树是否相等类似,唯一不同的是轴对称二叉树判断的是一颗二叉树的左节点与另一颗二叉树的右节点进行的判断。
时间复杂度 O ( N ) O(N) O(N)
空间复杂度 O ( N ) O(N) O(N)
5. 代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
//判断两颗二叉树是否是轴对称的
bool isAxisymmetric(struct TreeNode* root1, struct TreeNode* root2){
if(root1 == NULL && root2 == NULL){
return true;
}
if(root1 == NULL || root2 == NULL){
return false;
}
if(root1->val != root2->val){
return false;
}
return isAxisymmetric(root1->left, root2->right) &&
isAxisymmetric(root1->right, root2->left);
}
bool isSymmetric(struct TreeNode* root){
if(root == NULL){
return true;
}
//判断一颗二叉树是否是对称的,等价于判断二叉树的左子树是否与右子树轴对称
//等价于判断两颗二叉树是否是轴对称
//于是,把主根的左右节点分别看做两颗二叉树的主根,转化为判断两颗二叉树是否轴对称的问题
return isAxisymmetric(root->left, root->right);
}
四. 二叉树的前序遍历
1. 原题链接
2. 题目要求
给你二叉树的根节点 r o o t root root ,返回它节点值的 前序 遍历。
示例 1:
输入: r o o t = [ 1 , n u l l , 2 , 3 ] root = [1,null,2,3] root=[1,null,2,3]
输出: [ 1 , 2 , 3 ] [1,2,3] [1,2,3]
示例 2:
输入: r o o t = [ ] root = [] root=[]
输出: [ ] [] []
示例 3:
输入: r o o t = [ 1 ] root = [1] root=[1]
输出: [ 1 ] [1] [1]
示例 4:
输入: r o o t = [ 1 , 2 ] root = [1,2] root=[1,2]
输出: [ 1 , 2 ] [1,2] [1,2]
示例 5:
输入: r o o t = [ 1 , n u l l , 2 ] root = [1,null,2] root=[1,null,2]
输出: [ 1 , 2 ] [1,2] [1,2]
提示:
树中节点数目在范围 [ 0 , 100 ] [0, 100] [0,100] 内
? 100 < = N o d e . v a l < = 100 -100 <= Node.val <= 100 ?100<=Node.val<=100
3. 基础框架
- C版本的代码框架
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* preorderTraversal(struct TreeNode* root, int* returnSize){
}
4. 思路分析
(
1
)
(1)
(1)前序遍历的思路是:先访问根、然后是左子树、最后是右子树。
(
2
)
(2)
(2)以递归实现前序遍历:采用分治思想,对于当前根,先访问根,再访问左子树、最后访问右子树;子树再作为根重新进行上述流程,直到遇到空树。函数依次返回到上一级。
(
3
)
(3)
(3) 访问到的元素需要存到一个数组中,这个数组需要由我们来动态开辟,最后返回该数组名(数组首元素的地址)。而数组的大小也需要另外写一个函数计算,只需递归遍历一遍二叉树即可。
(
4
)
(4)
(4)访问根的操作包括把根节点所存的值赋给传入的数组,具体赋值给数组的哪个位置,有另一个参数pi控制应该赋值给数组的位置下标,之后pi加1。由于该参数的特殊功能,需要横跨多个递归调用的函数,所以其类型是指针类型,通过指针类型即可找到数组位置下标。
时间复杂度 O ( N ) O(N) O(N)
空间复杂度 O ( N ) O(N) O(N)
非递归前序遍历
(
1
)
(1)
(1)对二叉树的前序递归遍历时,会涉及到函数调用,函数栈帧的创建和销毁。先被调用的后销毁,后被调用的先销毁,这正好符合栈后进先出的原则,也就是说函数递归调用的过程相当于是有一个隐形的栈一样:
节点先入栈,然后依次入节点的左孩子,直到遇到空树返回到上一层调用;再入节点的右孩子。
(
2
)
(2)
(2)非递归前序遍历需要模拟递归调用的过程,把递归调用中隐形的栈给显式的模拟出来。
(
3
)
(3)
(3) 一开始先把树主根节点压栈,同时记录主根储存数据(先访问根),依次入当前根的左孩子(再访问左孩子),直到遇到空树就需要返回到上一层,对应的操作是取到栈顶的节点数据并临时保存,出栈一次;接着入栈临时保存节点的右孩子节点(最后访问右孩子),把入栈的节点看作新的根,重复上述操作。
(
4
)
(4)
(4)
时间复杂度 O ( N ) O(N) O(N)
空间复杂度 O ( N ) O(N) O(N)
5. 1递归代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
//计算整棵树的节点个数
int TreeSize(struct TreeNode* root){
if(root == NULL){
return 0;
}
return TreeSize(root->left) + TreeSize(root->right) + 1;
}
//前序遍历,以 根 - 左子树 - 右子树 的顺序
void PreOrder(struct TreeNode* root, int* arr, int* pi){
if(root == NULL){
return;
}
arr[*pi] = root->val;
(*pi)++;
PreOrder(root->left, arr, pi);
PreOrder(root->right, arr, pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
int num = TreeSize(root);
int* arr = (int*)malloc(sizeof(int)*num);
if(arr == NULL){
perror("malloc fail");
return NULL;
}
*returnSize = num;
int i = 0;
PreOrder(root, arr, &i);
return arr;
}
5.2 非递归代码实现 - 迭代
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
typedef struct TreeNode* STDataType;
typedef struct Stack {
STDataType* data;
int top;
int capacity;
}ST;
//初始化
void StackInit(ST* pst);
//销毁栈
void StackDestroy(ST* pst);
//入栈
void StackPush(ST* pst, STDataType val);
//出栈
void StackPop(ST* pst);
//取出栈顶元素
STDataType StackTop(ST* pst);
//判断栈是否是空
bool StackEmpty(ST* pst);
//返回栈的大小
int StackSize(ST* pst);
//初始化
void StackInit(ST* pst) {
assert(pst);
pst->data = NULL;
pst->top = pst->capacity = 0;
}
//销毁栈
void StackDestroy(ST* pst) {
assert(pst);
free(pst->data);
pst->top = pst->capacity = 0;
}
//入栈
void StackPush(ST* pst, STDataType val) {
assert(pst);
//扩容
if (pst->top == pst->capacity) {
int newCapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;
STDataType* tmp = (STDataType*)realloc(pst->data, sizeof(STDataType) * newCapacity);
if (!tmp) {
perror("StackPush");
}
pst->data = tmp;
pst->capacity = newCapacity;
}
pst->data[pst->top] = val;
++pst->top;
}
//出栈
void StackPop(ST* pst) {
assert(pst);
assert(!StackEmpty(pst));
--pst->top;
}
//取出栈顶元素
STDataType StackTop(ST* pst) {
assert(pst);
return pst->data[pst->top -1];
}
//判断栈是否是空
bool StackEmpty(ST* pst) {
assert(pst);
return pst->top == 0;
}
//返回栈的大小
int StackSize(ST* pst) {
assert(pst);
return pst->top;
}
int TreeSize(struct TreeNode* root){
if(root == NULL){
return 0;
}
return TreeSize(root->left) + TreeSize(root->right) + 1;
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
int num = TreeSize(root);
*returnSize = num;
int* arr = (int*)malloc(sizeof(int) * num);
//栈 后进先出,依次先根,再左子树,最后右子树
ST st;
StackInit(&st);
int i = 0;
struct TreeNode* cur = root;
while(!StackEmpty(&st) || cur != NULL){
//左子树
while(cur != NULL){
StackPush(&st, cur);
arr[i++] = cur->val;
cur = cur->left;
}
//回退上一节点,出栈本节点,再访问其右子树
cur = StackTop(&st);
StackPop(&st);
cur = cur->right;
}
StackDestroy(&st);
return arr;
}
五. 二叉树的中序遍历
1. 原题链接
2. 题目要求
给定一个二叉树的根节点 r o o t root root ,返回 它的 中序 遍历 。
示例 1:
输入: r o o t = [ 1 , n u l l , 2 , 3 ] root = [1,null,2,3] root=[1,null,2,3]
输出: [ 1 , 3 , 2 ] [1,3,2] [1,3,2]
示例 2:
输入: r o o t = [ ] root = [] root=[]
输出: [ ] [] []
示例 3:
输入: r o o t = [ 1 ] root = [1] root=[1]
输出: [ 1 ] [1] [1]
提示:
树中节点数目在范围 [ 0 , 100 ] [0, 100] [0,100] 内
? 100 < = N o d e . v a l < = 100 -100 <= Node.val <= 100 ?100<=Node.val<=100
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
3. 基础框架
- C版本的代码框架
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* inorderTraversal(struct TreeNode* root, int* returnSize){
}
4. 思路分析
递归思路见前序遍历
非递归中序遍历
5. 递归实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
//计算树节点个数
int TreeSize(struct TreeNode* root){
if(root == NULL){
return 0;
}
return TreeSize(root->left) + TreeSize(root->right) + 1;
}
//中序遍历
void InOrder(struct TreeNode* root, int* a, int* pi){
if(root == NULL){
return;
}
InOrder(root->left, a, pi);
a[*pi] = root->val;
(*pi)++;
InOrder(root->right, a, pi);
}
int* inorderTraversal(struct TreeNode* root, int* returnSize){
int num = TreeSize(root);
int* a = (int*)malloc(sizeof(int)*num);
if(a == NULL){
return NULL;
}
*returnSize = num;
//i标记数组下标,由于需要跨函数使用,所以传入了i的地址
int i = 0;
InOrder(root, a, &i);
return a;
}
迭代实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
typedef struct TreeNode* STDataType;
typedef struct Stack {
STDataType* data;
int top;
int capacity;
}ST;
//初始化
void StackInit(ST* pst);
//销毁栈
void StackDestroy(ST* pst);
//入栈
void StackPush(ST* pst, STDataType val);
//出栈
void StackPop(ST* pst);
//取出栈顶元素
STDataType StackTop(ST* pst);
//判断栈是否是空
bool StackEmpty(ST* pst);
//返回栈的大小
int StackSize(ST* pst);
//初始化
void StackInit(ST* pst) {
assert(pst);
pst->data = NULL;
pst->top = pst->capacity = 0;
}
//销毁栈
void StackDestroy(ST* pst) {
assert(pst);
free(pst->data);
pst->top = pst->capacity = 0;
}
//入栈
void StackPush(ST* pst, STDataType val) {
assert(pst);
//扩容
if (pst->top == pst->capacity) {
int newCapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;
STDataType* tmp = (STDataType*)realloc(pst->data, sizeof(STDataType) * newCapacity);
if (!tmp) {
perror("StackPush");
}
pst->data = tmp;
pst->capacity = newCapacity;
}
pst->data[pst->top] = val;
++pst->top;
}
//出栈
void StackPop(ST* pst) {
assert(pst);
assert(!StackEmpty(pst));
--pst->top;
}
//取出栈顶元素
STDataType StackTop(ST* pst) {
assert(pst);
return pst->data[pst->top -1];
}
//判断栈是否是空
bool StackEmpty(ST* pst) {
assert(pst);
return pst->top == 0;
}
//返回栈的大小
int StackSize(ST* pst) {
assert(pst);
return pst->top;
}
int TreeSize(struct TreeNode* root){
if(root == NULL){
return 0;
}
return TreeSize(root->left) + TreeSize(root->right) + 1;
}
int* inorderTraversal(struct TreeNode* root, int* returnSize){
int num = TreeSize(root);
int* arr = (int*)malloc(sizeof(int) * num);
*returnSize = num;
int i=0;
ST st;
StackInit(&st);
struct TreeNode* cur = root;
while(!StackEmpty(&st) || cur != NULL){
//入栈左子树一直到空树
while(cur != NULL){
StackPush(&st, cur);
cur = cur->left;
}
//入栈右子树
cur = StackTop(&st);
//中序遍历,左子树先被记录,所以是记录出栈的数据
arr[i++] = cur->val;
StackPop(&st);
cur = cur->right;
}
StackDestroy(&st);
return arr;
}
六. 二叉树的后序遍历
1. 原题链接
2. 题目要求
给你一棵二叉树的根节点 r o o t root root ,返回其节点值的 后序 遍历 。
示例 1:
输入: r o o t = [ 1 , n u l l , 2 , 3 ] root = [1,null,2,3] root=[1,null,2,3]
输出: [ 3 , 2 , 1 ] [3,2,1] [3,2,1]
示例 2:
输入: r o o t = [ ] root = [] root=[]
输出: [ ] [] []
示例 3:
输入: r o o t = [ 1 ] root = [1] root=[1]
输出: [ 1 ] [1] [1]
提示:
树中节点的数目在范围 [ 0 , 100 ] [0, 100] [0,100] 内
? 100 < = N o d e . v a l < = 100 -100 <= Node.val <= 100 ?100<=Node.val<=100
进阶:递归算法很简单,你可以通过迭代算法完成吗?
3. 基础框架
- C版本的代码框架
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* postorderTraversal(struct TreeNode* root, int* returnSize){
}
4. 思路分析
后序遍历递归思路见前序遍历递归
非递归后序遍历
5. 递归实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
// 计算树节点个数
int TreeSize(struct TreeNode* root){
if(root == NULL){
return 0;
}
return TreeSize(root->left) + TreeSize(root->right) + 1;
}
//后序遍历
void PostOrder(struct TreeNode* root, int* a, int *pi){
if(root == NULL){
return;
}
PostOrder(root->left, a, pi);
PostOrder(root->right, a, pi);
a[*pi] = root->val;
(*pi)++;
}
int* postorderTraversal(struct TreeNode* root, int* returnSize){
int num = TreeSize(root);
int* a = (int*)malloc(sizeof(int)*num);
if(a == NULL){
return NULL;
}
*returnSize = num;
int i = 0;
PostOrder(root, a, &i);
return a;
}
迭代实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
typedef struct TreeNode* STDataType;
typedef struct Stack {
STDataType* data;
int top;
int capacity;
}ST;
//初始化
void StackInit(ST* pst);
//销毁栈
void StackDestroy(ST* pst);
//入栈
void StackPush(ST* pst, STDataType val);
//出栈
void StackPop(ST* pst);
//取出栈顶元素
STDataType StackTop(ST* pst);
//判断栈是否是空
bool StackEmpty(ST* pst);
//返回栈的大小
int StackSize(ST* pst);
//初始化
void StackInit(ST* pst) {
assert(pst);
pst->data = NULL;
pst->top = pst->capacity = 0;
}
//销毁栈
void StackDestroy(ST* pst) {
assert(pst);
free(pst->data);
pst->top = pst->capacity = 0;
}
//入栈
void StackPush(ST* pst, STDataType val) {
assert(pst);
//扩容
if (pst->top == pst->capacity) {
int newCapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;
STDataType* tmp = (STDataType*)realloc(pst->data, sizeof(STDataType) * newCapacity);
if (!tmp) {
perror("StackPush");
}
pst->data = tmp;
pst->capacity = newCapacity;
}
pst->data[pst->top] = val;
++pst->top;
}
//出栈
void StackPop(ST* pst) {
assert(pst);
assert(!StackEmpty(pst));
--pst->top;
}
//取出栈顶元素
STDataType StackTop(ST* pst) {
assert(pst);
return pst->data[pst->top -1];
}
//判断栈是否是空
bool StackEmpty(ST* pst) {
assert(pst);
return pst->top == 0;
}
//返回栈的大小
int StackSize(ST* pst) {
assert(pst);
return pst->top;
}
int TreeSize(struct TreeNode* root){
if(root == NULL){
return 0;
}
return TreeSize(root->left) + TreeSize(root->right) + 1;
}
int* postorderTraversal(struct TreeNode* root, int* returnSize){
int num = TreeSize(root);
int* arr = (int*)malloc(sizeof(int) * num);
*returnSize = num;
int i=0;
ST st;
StackInit(&st);
struct TreeNode* cur = root;
struct TreeNode* prev = prev;
while(!StackEmpty(&st) || cur != NULL){
//入栈左子树一直到空树
while(cur != NULL){
StackPush(&st, cur);
cur = cur->left;
}
cur = StackTop(&st);
StackPop(&st);
//prev作用:记录上一个入数组的节点地址,防止已经入栈的右节点再次入栈造成死循环
//节点右孩子不存在
if(cur->right == NULL || cur->right == prev){
prev = cur;
cur = NULL;
arr[i++] = prev->val;
}
else{
StackPush(&st, cur);
cur = cur->right;
}
}
StackDestroy(&st);
return arr;
}
七. 另一棵树的子树
1. 原题链接
2. 题目要求
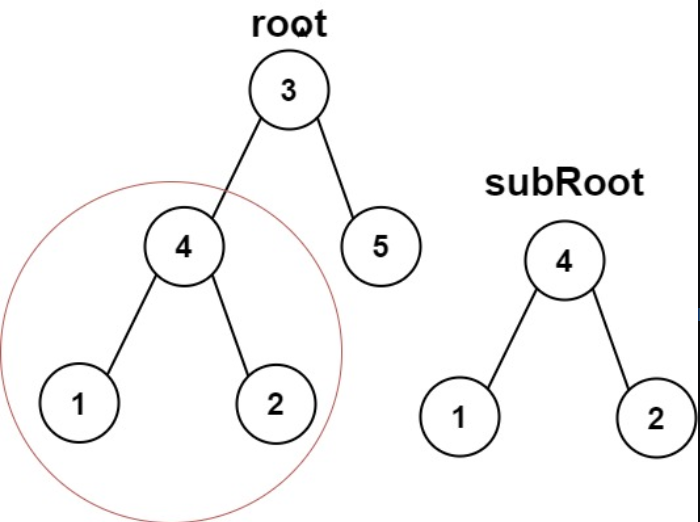
给你两棵二叉树 r o o t root root 和 s u b R o o t subRoot subRoot 。检验 r o o t root root 中是否包含和 s u b R o o t subRoot subRoot 具有相同结构和节点值的子树。如果存在,返回 t r u e true true ;否则,返回 f a l s e false false 。
二叉树 t r e e tree tree 的一棵子树包括 t r e e tree tree 的某个节点和这个节点的所有后代节点。 t r e e tree tree 也可以看做它自身的一棵子树。
示例 1:
输入: r o o t = [ 3 , 4 , 5 , 1 , 2 ] , s u b R o o t = [ 4 , 1 , 2 ] root = [3,4,5,1,2], subRoot = [4,1,2] root=[3,4,5,1,2],subRoot=[4,1,2]
输出: t r u e true true
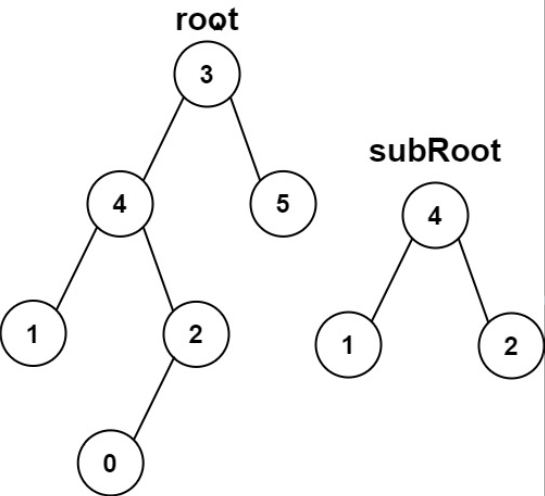
示例 2:
输入: r o o t = [ 3 , 4 , 5 , 1 , 2 , n u l l , n u l l , n u l l , n u l l , 0 ] , s u b R o o t = [ 4 , 1 , 2 ] root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2] root=[3,4,5,1,2,null,null,null,null,0],subRoot=[4,1,2]
输出: f a l s e false false
提示:
r o o t root root 树上的节点数量范围是 [ 1 , 2000 ] [1, 2000] [1,2000]
s u b R o o t subRoot subRoot 树上的节点数量范围是 [ 1 , 1000 ] [1, 1000] [1,1000]
? 104 < = r o o t . v a l < = 104 -104 <= root.val <= 104 ?104<=root.val<=104
? 104 < = s u b R o o t . v a l < = 104 -104 <= subRoot.val <= 104 ?104<=subRoot.val<=104
3. 基础框架
- C版本的代码框架
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
}
4. 思路分析
(
1
)
(1)
(1)在一颗二叉树root1中找另外一颗二叉树root2,可以看作是分别以root1中每个节点为根而形成的二叉树分别与root2相比较。
(
2
)
(2)
(2) 即转换为了两个二叉树是否相当的问题。
(
3
)
(3)
(3)采用分治思想,看成根和左右子树。每次都以当前跟为起点,看作一颗二叉树,然后与待比较二叉树root2比较,如果相等就是找到了,函数返回true;如果没找到,就继续在子树中找,直到遇到空树也没找到,就返回false
5. 代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
//判断两个树是否相等
bool isEqual(struct TreeNode* root1, struct TreeNode* root2){
if(root1 == NULL && root2 == NULL){
return true;
}
if(root1 && root2 == NULL){
return false;
}
if(root1 == NULL && root2){
return false;
}
if(root1->val != root2->val){
return false;
}
return isEqual(root1->left, root2->left) &&
isEqual(root1->right, root2->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
//当前节点为空就直接返回上一层
if(root == NULL){
return false;
}
//判断以当前节点为根的树是否与待比较的树相等
//相等就直接返回true,不相等就继续找,直到为空树返回false
if(isEqual(root, subRoot)){
return true;
}
//到这里说明以当前节点为根的子树与待比较树不相等
//于是将在左右子树中继续找,由于只需找到一个相等的情况,所以结果是||的关系
return isSubtree(root->left, subRoot) ||
isSubtree(root->right, subRoot);
}
结语
本文到这里就结束了,不过向前的时光并没有结束,感谢看到这里的你!
E N D END END