文章目录
1.24两两交换链表中的节点
1.1.题目
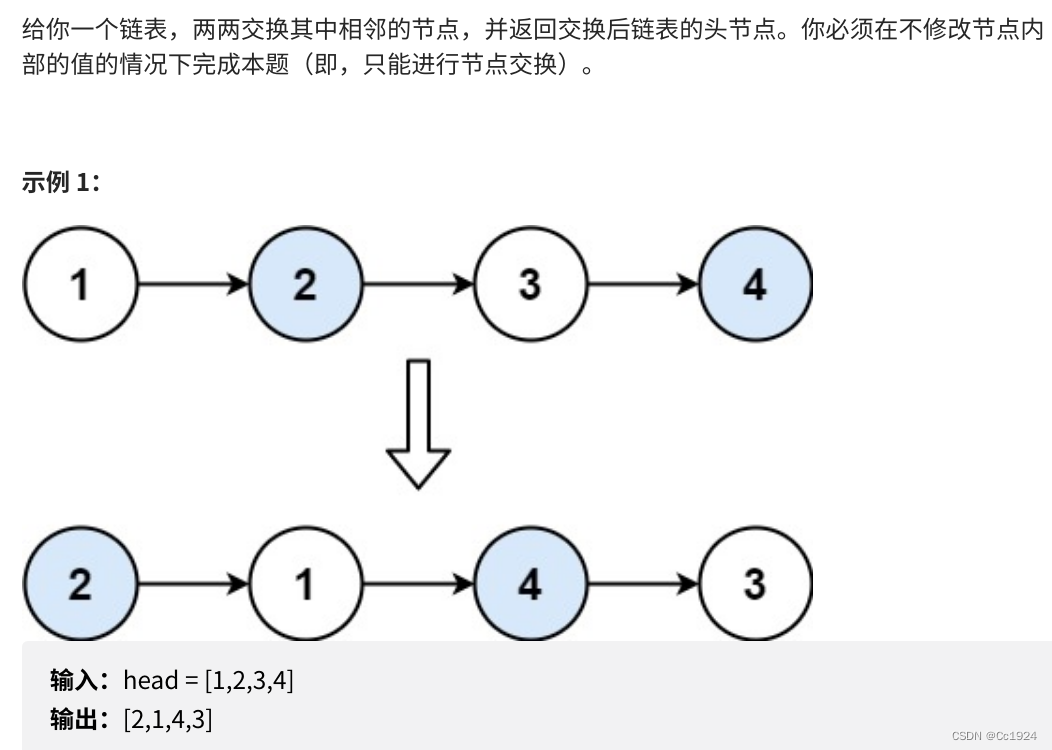
1.2.思路
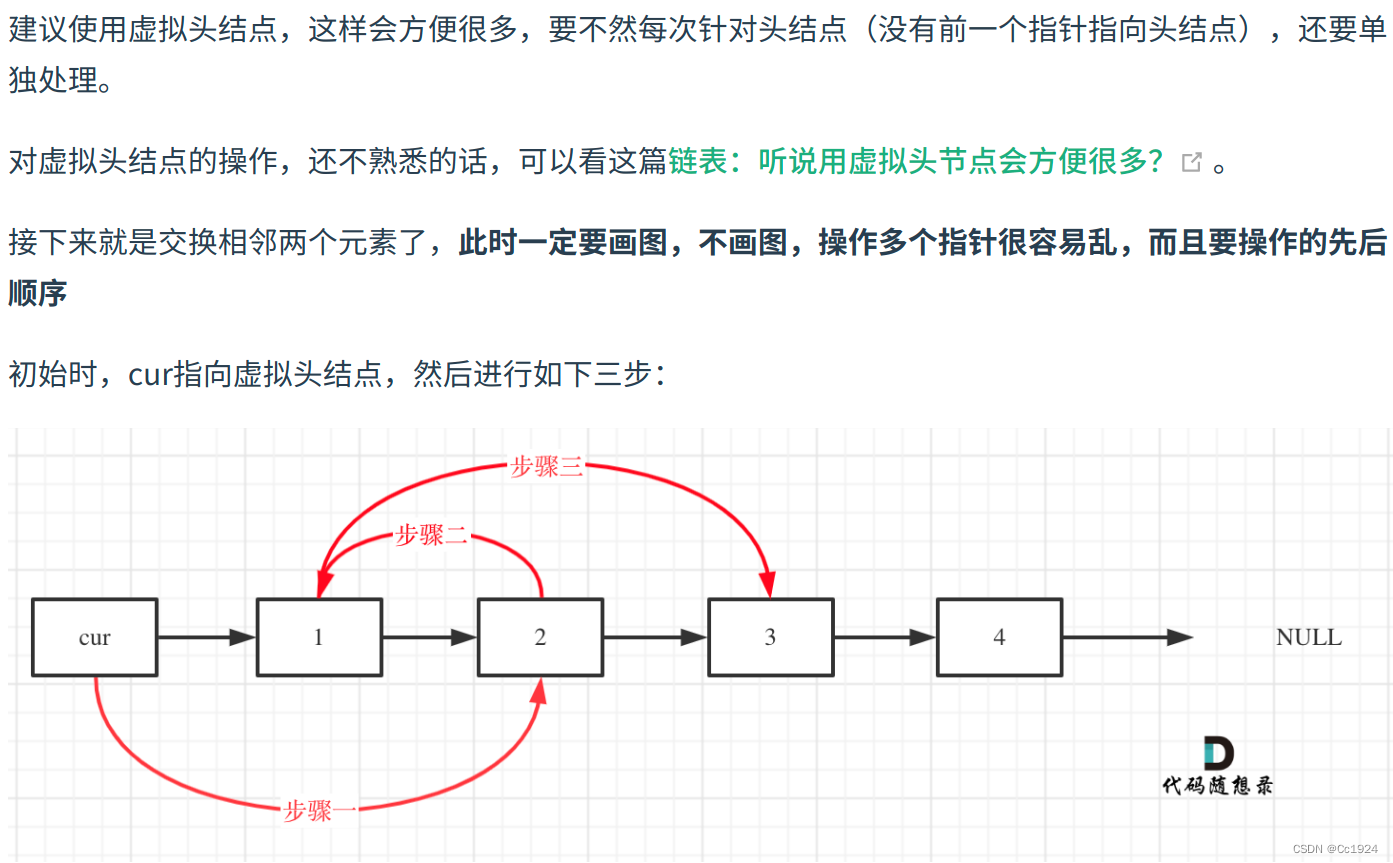
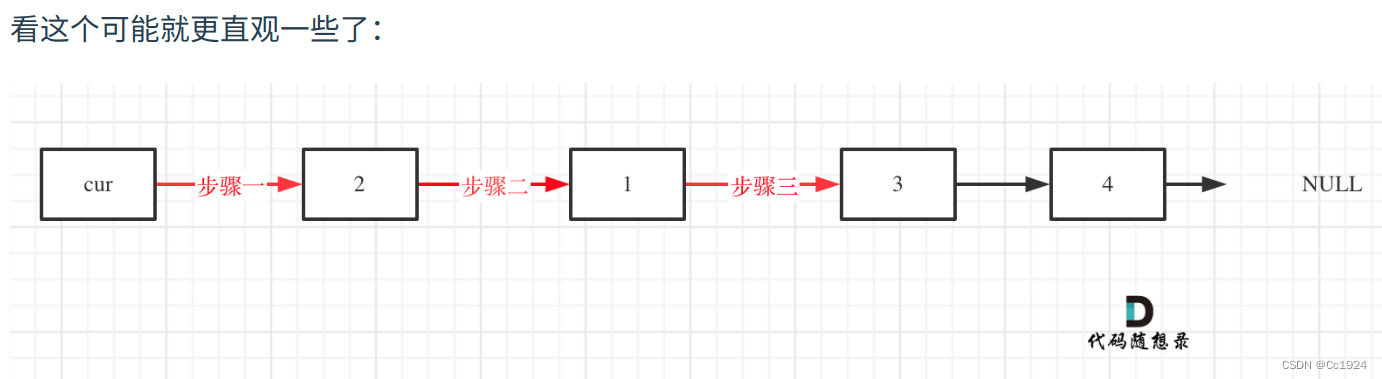
实际上,仔细看上面的图之后还是得到了链表原来那个非常重要的性质:即操作当前节点,一定要通过上一个节点进行访问,因为需要修改上一个节点的next指针新的指向。因此本题虽然是交换相邻的两个节点BC,但是始终会从B的上一个节点A开始操作,即虽然是只交换两个节点,但是操作的时候始终是在操作3个节点,就是因为对链表结构进行修改之后,需要更新其上一个节点的next指针,因此一直需要从A节点开始操作。
比如上面的最后一个图,当交换完1和2之后,cur指向了1的位置,但是实际上下面我们是要交换3和4,此时再次使用原来的套路,1指向4,4指向3,3再指向4后面的那个元素,可见此时仍然是成立的。
1.3.代码实现
1.3.1.对next指针的理解
今天发现在代码编程中对next理解的还是不清晰,有的时候把他认为是当前节点的next指针变量,有的时候又把它理解成当前节点的下一个节点。显然这两种理解都是正确的,但是不同的场景下需要使用切换不同的理解方式,显然很麻烦。比如cur->next = tmp,这个就把next理解成当前节点的指针变量;如果是cur->next->val = 1,这又要把next理解成当前节点的下一个节点。这样切换很难受。
实际上,只需要把next理解成从节点出来的、指向下一个节点的箭头即可。这样理解永远不会出错,而不用区分他到底是指针变量还是指向的下一个节点。所以后面统一记为next箭头。
更新:评论中有人对next指针进行了评价,这促使我对next指针又得到了新的理解。
上面自己说对next指针有两种理解,实际上本质原因就在于next指针是归属于两个节点的,它是链接两个节点的桥梁。对于前一个节点来说,next指针就是它的成员变量,此时它就是一个指针变量,比如cur->next = tmp就是在修改这个变量的值。而对于后一个节点来说,上一个节点的next指向的就是当前这个节点的内存地址,所以如果是cur->next->val = 1,那么此时上一个节点的next就相当于是当前节点,此时next就是指针指向的节点。因此是next指针对前后两个节点的联系,导致了它可以有两种不同的理解。
如果统一把next理解成从当前节点出来的、指向下一个节点的箭头:对于cur->next = tmp,就是修改当前节点的箭头指向的方向,让它指向tmp节点; 对于cur->next->val = 1,就是在访问当前节点的箭头指向的节点的值。
1.3.2.编程中要备份哪些节点的指针?
其实很简单,只要是破坏了链表的索引结构,那么都需要备份节点的指针。什么时候会破坏链表的索引结构呢?其实就是修改next箭头的时候。
因此总结为:修改了某个节点的next箭头,此时该节点的下一个节点索引丢失,因此要备份该节点的下一个节点。
1.3.3.代码实现
class Solution
{
public:
struct ListNode
{
int val;
ListNode* next;
ListNode(int x): val(x), next(nullptr){}
ListNode(int x, ListNode* ptr): val(x), next(ptr){}
};
ListNode *swapPairs(ListNode *head)
{
ListNode* dummy_node = new ListNode(0);
dummy_node->next = head;
// 链表举例: [cur, 1, 2, 3, 4]
// 索引位置: [cur, 1, 2, 3, 4]
ListNode* cur = dummy_node; // 从虚拟头节点0开始
// 要交换的是第1和2个节点,因此他们不能是空
while(cur->next != nullptr && cur->next->next != nullptr)
{
// 关于要备份哪些节点,实际上可以先编程后面,发现哪里缺了再在这里备份
ListNode* tmp1 = cur->next;
ListNode* tmp3 = cur->next->next->next;
// 步骤1:cur的箭头指向第2个节点,由于cur的箭头被修改,因此需要备份它原来箭头指向的节点,即tmp1
cur->next = cur->next->next;
// 步骤2:第2个节点的箭头指向第1个节点,由于第2个节点的箭头被修改,因此要备份它原来箭头指向的节点,即tmp3
cur->next->next = tmp1;
// 步骤3:第1个节点的箭头指向第3个节点
cur->next->next->next = tmp3;
cur = cur->next->next; // 最后,cur跳两个位置,交换下两个节点
}
return dummy_node->next; // 返回交换后的链表的头指针
}
};
2.19删除链表的倒数第N个节点
2.1.题目
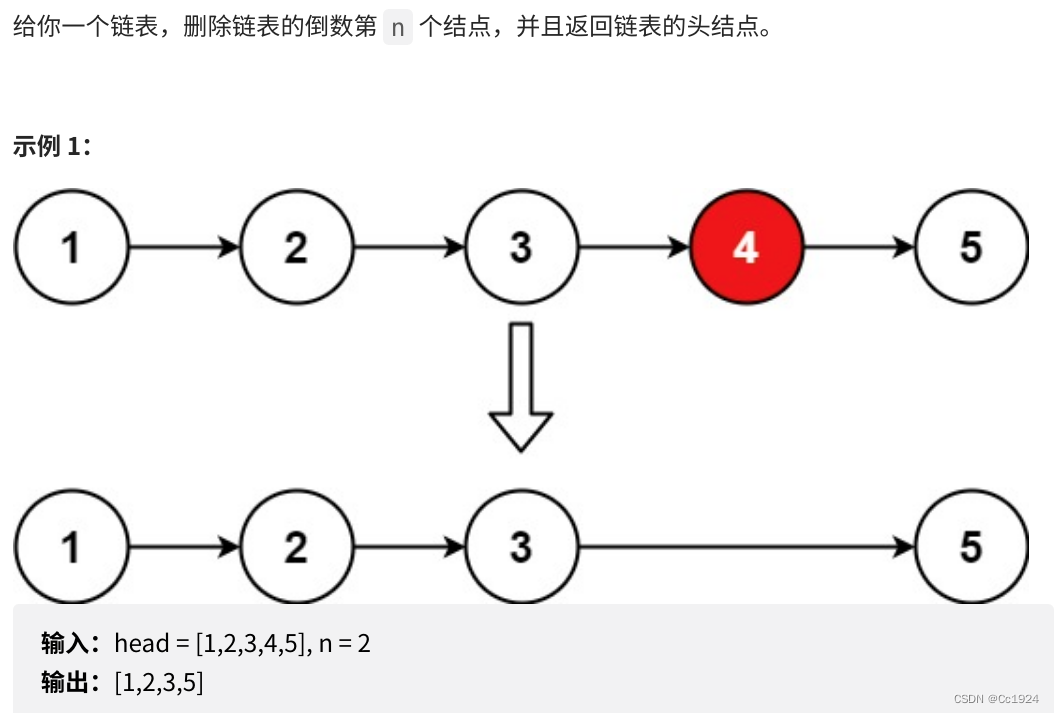
2.2.思路
注意这里是求倒数第n个节点,一个比较简单的思路是把原来的链表先遍历一遍,求出来它一共有多少个节点N,然后再把总结点数N减去n,就得到了正向数要删除的是第几个节点N-n。这样再次遍历列表到第N-n个节点,对这个节点进行删除。但是很显然这样两个for循环遍历,复杂度是n^2。
另外一个很好的解法是使用双指针,一个fast和一个slow指针都指向虚拟头节点,然后fast指针先向后移动n,然后fast和slow一起向后移动,直到fast移动到最后一个节点,此时slow也就移动到了要被删除的节点。
class Solution
{
public:
struct ListNode
{
int val;
ListNode* next;
ListNode(int x): val(x), next(nullptr){}
ListNode(int x, ListNode* ptr): val(x), next(ptr){}
};
ListNode *removeNthFromEnd(ListNode *head, int n)
{
ListNode* dummy_node = new ListNode(0, head);
ListNode* fast = dummy_node;
ListNode* slow = dummy_node;
while(n-- && fast->next != nullptr)
{
fast = fast->next;
}
// 至此fast->next就是第n个节点
while(fast->next != nullptr)
{
fast = fast->next;
slow = slow->next;
}
// 至此fast指向最后一个节点,slow的下一个节点就是倒数第n个节点,就是要被删除的节点
ListNode* tmp = slow->next;
// 这里修改了next箭头的指向,因此上面要备份原来的next箭头指向的节点
slow->next = slow->next->next;
delete tmp;
return dummy_node->next;
}
};
3.面试题02.07链表相交
3.1.题目

3.2.解答
其实链表相交很简单,一定满足是在后面相交的。所以只需要把两个链表在尾部对齐,然后从短的链表的开头开始遍历,比较两个链表对应节点的指针是否相等, 如果相等就找到了相交点。
class Solution
{
public:
struct ListNode
{
int val;
ListNode *next;
ListNode(int x) : val(x), next(nullptr) {}
};
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB)
{
int len_a = 0;
int len_b = 0;
ListNode* cur_a = headA;
ListNode* cur_b = headB;
// 查询AB两个链表的总长度
while(cur_a != nullptr)
{
len_a++;
cur_a = cur_a->next;
}
while(cur_b != nullptr)
{
len_b++;
cur_b = cur_b->next;
}
// 把两个指针恢复到头指针
cur_a = headA;
cur_b = headB;
int offset = len_a - len_b;
if(offset > 0)
{
while(offset--)
{
cur_a = cur_a->next;
}
}
else
{
offset = -offset;
while(offset--)
{
cur_b = cur_b->next;
}
}
while(cur_a != nullptr)
{
if(cur_a == cur_b)
{
return cur_b;
}
else
{
cur_a = cur_a->next;
cur_b = cur_b->next;
}
}
return nullptr;
}
};
4.142.环形链表II
4.1.题目
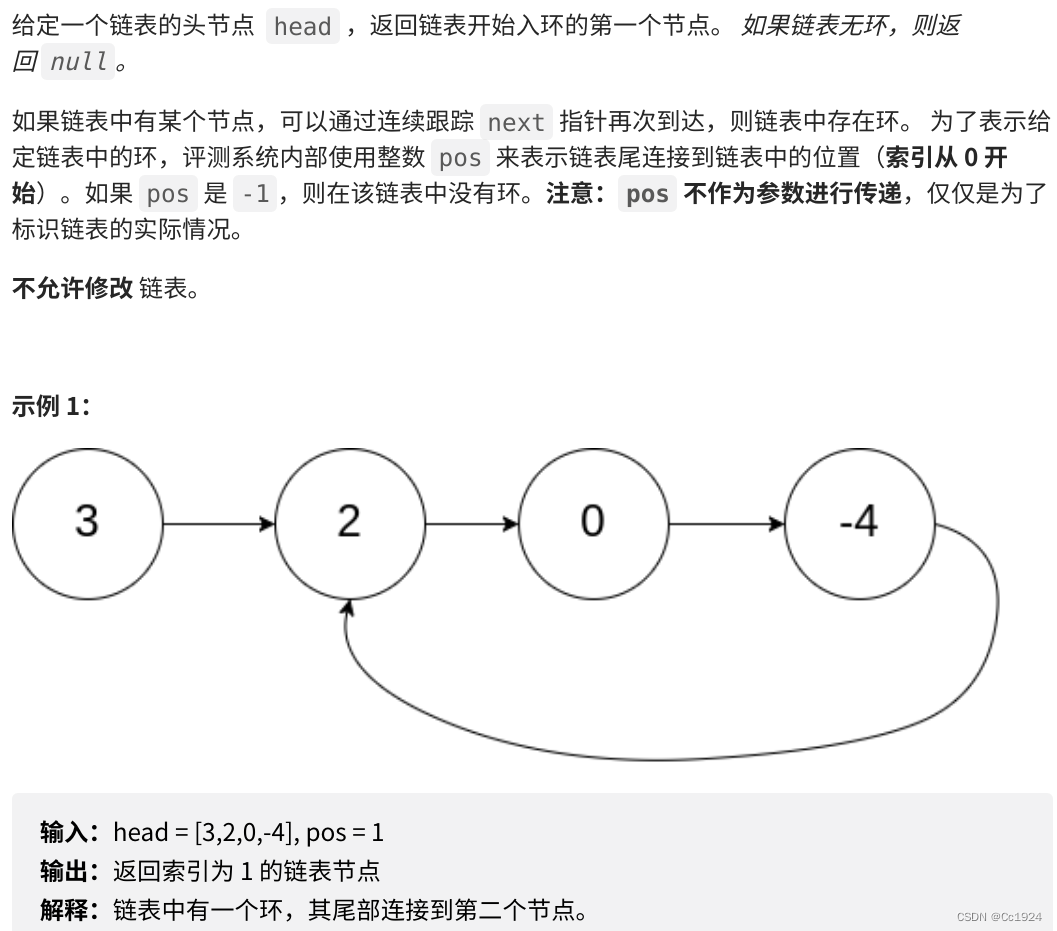
4.2.思路
整体思路都是参考代码随想录中的讲解,详细内容去看讲解吧,本题还是比较复杂的,从判断是否有环,到计算环的第一个入口点,都有很多分析。
注意在其中有几个问题:
- 为什么
fast指针走两步,slow指针走一步,如果有环的话他们一定会相遇呢?
其实这个问题根据讲解分为两步:
(1)如果有环,那么一定是fast先进入环。这个很容易理解,因为fast走的快嘛。
(2)当slow指针进入环之后,此时只要fast指针没有立即和slow指针相遇,那么不论fast指针在什么地方,都可以把slow指针认为是在前面运动的指针,然后fast指针就在追slow指针。fast指针每次都比slow指针多走一步,因此fast指针在一步一步的追slow指针,他们之间的距离就是一步一步的在减小,因此他们一定会相遇,最多追赶的次数也就是y+z-1次,其中y+z是环的节点个数。
为什么最多的追赶次数是y+z-1次?因为slow刚进入环的时候,如果fast此时也在环的入口点,此时他们直接就相遇了,不用追赶,追赶次数就是0次。只要fast不在环的入口点,按照上面的理解,此时一律都认为slow指针在前面,fast指针在后面追slow指针。那么追的最大次数也就是fast指针恰好在slow指针的下一个节点上,然后fast指针就要比slow指针多走y+z-1次才能追上slow指针,也就是就差一步就追完一圈,这差的一步就是刚开始的时候fast指针在slow指针的下一个节点导致的。
- 计算入口节点的时候,为什么
slow指针在环内走过的长度只可能是y,而不是n*(y+z) + y呢?即slow指针不可能走完一圈?
其实这个问题在上面的问题中已经得到了解答,就是如果slow在刚进入环的时候如果和fast没有相遇,那么fast就要一步一步的去追slow,而且此时追slow需要的步骤次数最多就是y+z-1次,即不会走完一个环,所以说slow指针被fast指针追上之前,在环内肯定不可能走完一圈,最大的长度也就是走y+z-1步,也就是从环的入口开始,走到环的入口的前一个点,此时恰好被fast追上。实际上,这种情况对应的是在slow刚进入环的时候,fast恰好在环的入口的下一个节点上,然后fast就需要追y+z-1步才能追上slow指针。
- 最后计算相遇节点的时候,得到的公式是
x = (n-1)*(y+z) + z,n=1时x=z,为什么n>1时结果和n=1时结果一样?
其实从分析这个公式就可以知道,即一个指针从起点开始,另一个指针从相遇点开始,每次每人各走一步,最后走完x步以后他们一定会在环的起点相遇。此时如果n>1,就相当于另一个指针在环中等了从head出发的第一个指针很久,在环里绕了很多次了。但是最后的结果他们还是会在环的入口处相遇的。
class Solution
{
public:
struct ListNode
{
int val;
ListNode *next;
ListNode(int x) : val(x), next(NULL) {}
};
ListNode *detectCycle(ListNode *head)
{
ListNode* fast = head;
ListNode* slow = head;
// 注意这里只判断到fast->next即可,不需要判断到fast->next->next
while(fast != nullptr && fast->next != nullptr)
{
// 这里一定要先移动再判断,而不能上来就判断是否相等,因为一开始他俩都是head,肯定是相等的
fast = fast->next->next;
slow = slow->next;
// 找到了环的入口点
if(fast == slow)
{
// 让一个新的指针从head出发,然后每次走一步,最终会和slow指针在环的入口点相遇
ListNode* new_slow = head;
while(new_slow != slow)
{
new_slow = new_slow->next;
slow = slow->next;
}
return new_slow;
}
}
return nullptr;
}
};