难度简单352
请实现一个函数,把字符串?
s?中的每个空格替换成"%20"。示例 1:
输入:s = "We are happy." 输出:"We%20are%20happy."限制:
0 <= s 的长度 <= 10000
class Solution {
public String replaceSpace(String s) {
//在java中String是不可以被修改的 ,所以要在借用一个数组来重新写
//StringBuilder 是被允许在与原来的对象上进行多次修改 ,一个一个字符
//所以只需要在遇到空格将他替换成%20 剩下的就直接复制就行
StringBuilder sb=new StringBuilder();
for(Character c : s.toCharArray()){//toCharArray() 方法将字符串转换为字符数组
if(c==' ') sb.append("%20");
else sb.append(c);
}
return sb.toString();//最后要将StringBUilder类型转成String类型
}
}?注意:本题主要考察java中String类的对象,不能被修改;要使用StringBuffer或StringBuilder类,它们允许字符串进行修改。
(1)先将String类型转换成数组(使用toCharArray()方法)
(2)创建StringBuilder对象,进行字符串的拼接。
?(3)别忘了转型,调用toString()方法。
String StringBuffer和?StringBuilder的区别:
String字符串常量,不能被修改。StringBuilder和StringBuffer可以在内存中频繁修改。
同时StringBuilder是线程安全的类,StringBuffer是线程不安全的类。
速度:
String<StringBuffer<StringBuilder
输入一个链表的头节点,从尾到头反过来返回每个节点的值(用数组返回)。
示例 1:
输入:head = [1,3,2]
输出:[2,3,1]
?限制:
0 <= 链表长度 <= 10000
这道题有两种思路:
一 利用栈,这种数据结构 栈先进后出 ,刚好满足题意。
(1)利用集合LinkedList类(底层是双向链表) 先将链表中的数据存起来
(2)利用数组存储反向连表里的数据
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public int[] reversePrint(ListNode head) {//链表 转成栈
LinkedList<Integer> arr =new LinkedList<Integer>();//利用集合
//链表是 data和next 指针 组成
while(head!=null){
arr.addLast(head.val);//如果当前值不为空,那我就把当前这个值存起来
head=head.next;//head.next 就是下一个值
}
int[] res =new int[arr.size()];//获取集合长度 size()
for(int i=0;i<res.length;i++){
res[i]=arr.removeLast();//集合从最后一个数开始赋值 出来后就变成 倒序排列了
//removeLast() 删除并返回最后一个
}
return res;
}
}
第二种运用递归:如下图:

/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
LinkedList<Integer> arr =new LinkedList<Integer>();//使用链表
public int[] reversePrint(ListNode head) {//使用递归
res(head);
int[] end =new int[arr.size()];
for(int i=0;i<end.length;i++){
end[i]=arr.removeFirst();
}
return end;
}
public void res(ListNode head){
//设置递归终止条件
if(head==null) return ;
res(head.next);//如果head不为空,那就调用
//当递归到最后 一层一层存储。
arr.add(head.val);
}
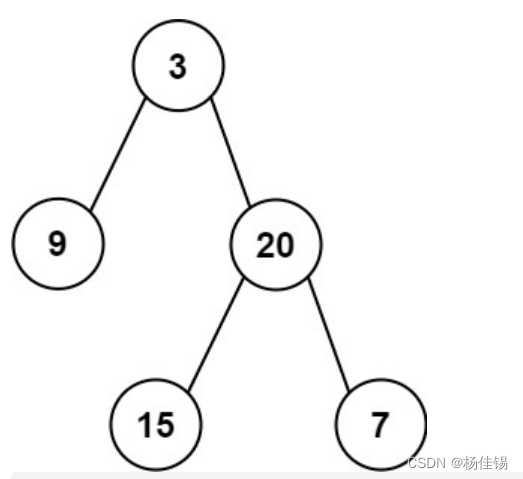
}输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
示例 1:
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
示例 2:?
Input: preorder = [-1], inorder = [-1]
Output: [-1]
?限制:
0 <= 节点个数 <= 5000
?前提:一般与二叉树有关的题目 都与分治和递归的算法有关。
我们都知道二叉树有前序,中序,后序遍历。
四种主要的遍历思想为:
前序遍历:根结点 ---> 左子树 ---> 右子树
中序遍历:左子树--->?根结点?---> 右子树
后序遍历:左子树 ---> 右子树?---> 根结点
层次遍历:只需按层次遍历即可。
当已知前序和中序遍历时就可以确定一棵二叉树。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
//前序遍历和中序遍历可以确定一颗二叉树 我只要知道前序遍历的第一个数一定是这棵树的根节点,那我就可以知道中序遍历中
//左右子树的位置
//解题思路:二叉树题目一般与分治 和 递归算法有关
//1.先确定根节点 前序遍历第一个数就是根节点 root
//2.找到左子树的个数 在中序中找到根节点(由前序可得) index,确定左子树的长度 int left =index-inStart
//3.创建二叉树 左右节点递归
//递归
// 1 明确递归结束条件 在二叉树中 左子树一定要小于右子树
// 2 每次找的步骤都是相同的
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
//使用递归,建立函数
return rebuildTree(preorder,0,preorder.length-1,inorder,0,inorder.length-1);
}
//使用递归
public TreeNode rebuildTree(int[] preorder,int preStart,int preEnd ,int[] inorder,int inStart,int inEnd){
//1。确定递归结束条件
if(preStart>preEnd){
return null;
}
//确定根节点--有前序遍历可知
int root=preorder[preStart];
int index=0;
//找到中序遍历的根节点的位置--中序遍历可知
for(int i=0;i<inorder.length;i++){
if(inorder[i]==root){
index=i;
break;
}
}
TreeNode node=new TreeNode(root);
//左子树的大小--中序遍历
int left=index-inStart;
//递归调用 左右节点 根据前序遍历数组中的下标创建
node.left=rebuildTree(preorder,preStart+1,preStart+left,inorder,inStart,index-1);
node.right=rebuildTree(preorder,preStart+left+1,preEnd,inorder,index+1,inEnd);
return node;
}
}(1)首先根据前序遍历可知根节点
(2)然后在中序遍历中找到根节点,确定左子树的长度 中序遍历中 根节点位置-初始位置
(3)递归调用左右子节点