引言
对于任何一个程序员来说,可能都不会陌生。你学的第一个算法,可能就是排序。排序算法有很多很多,我们只聊聊最常用的:冒泡排序、插入排序、选择排序、归并排序、快速排序、计数排序、基数排序、桶排序。我们分三次文章来学习。
一、如何分析一个排序算法
一般从以下几个方面衡量:
1.1 执行效率
- 最好、最坏、平均时间复杂度
为什么要区分不同的时间复杂度呢?对于待排序的数据,有的接近有序,有的完全乱序,不同的数据源对排序算法的性能还是有影响的。 - 时间复杂度系数,常数、低阶
时间复杂度描述的是排序算法耗时随着数据规模n增加而增加的趋势。但实际开发过程中,我们要排序的数据都在数百数千的量级,所以低阶及常数系数也是我们要考虑的点。 - 比较和移动的元素的次数
基于比较的排序的排序算法,在执行过程中一般会经历两步,第一比较两个元素的大小;第二移动相应的元素。
1.2 内存消耗
简单理解就是排序需不需要再开辟新的空间,不需要开辟新空间就是原地排序,空间复杂度是O(1),否则就是O(n)。
1.3 稳定性
稳定性指的是,如果待排序的数据中如果有相等的元素,在排序后相等元素的相对位置没有发生变化就是稳定的,否则就是不稳定的排序算法。举个例子:
待排序数据:5 2 8 3 5 4
排序后: 2 3 4 5 5 8
待排序数据中,下标为0 和 5的元素都是5,如果是稳定的排序算法,则在排序后,下标为0的那个5在下标为5的元素前面。
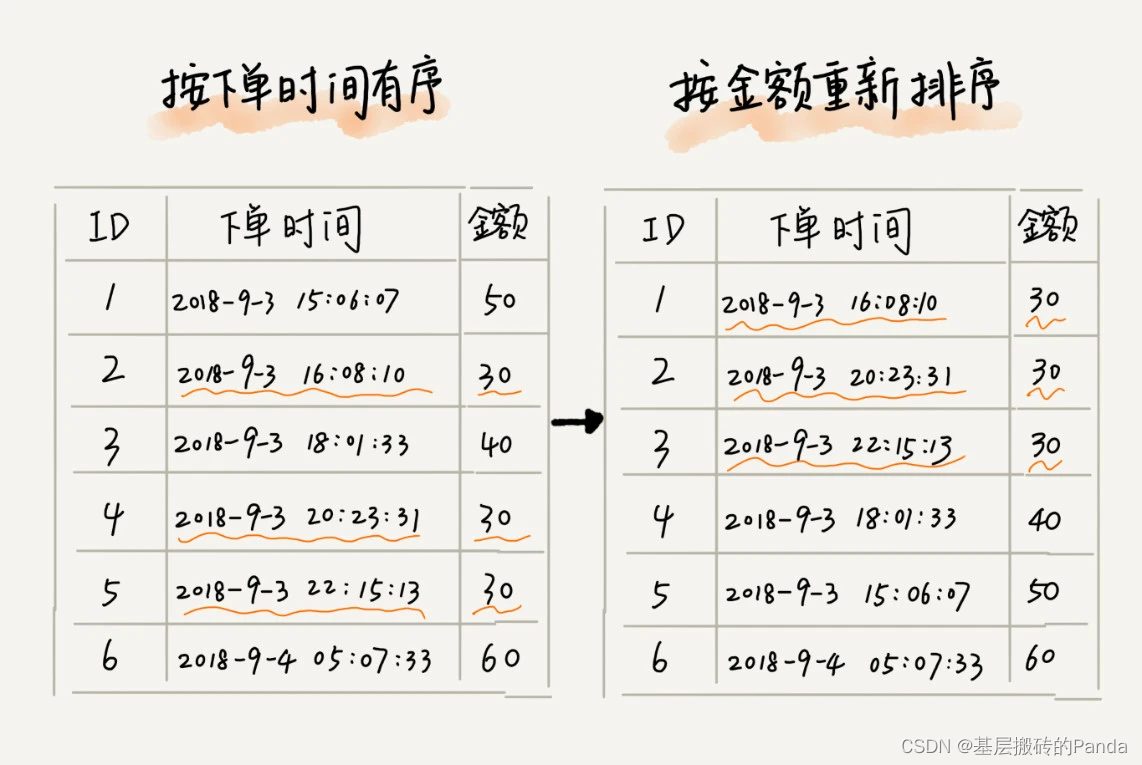
为什么要有稳定性呢?我们来看一个例子:假如现在需要对一个电商的“订单”进行排序,订单有两个属性,一个是下单时间,另一个是购买金额。假设现在需要按照金额从小到达进行排序,如果金额相同按照下单时间的早晚进行排序。怎么做呢?
这里就可以利用排序的稳定性,我们可以先按照下单时间的早晚进行排序,此时所有的订单就是按照下单时间早晚有序了,再按照下单金额进行排序,就可以得到结果了。这是因为排序的稳定性,排序后下单时间的早晚的相对顺序不会发生变化。
二、排序算法(冒泡、插入和选择排序)
2.1 冒泡排序
思路:每次只比较相邻的两个元素,如果不满足大小关系就交换他们的位置,每经过一次冒泡,一个元素就被放在了它应该在的位置。重复n次,直到所有的数据都有序。
我们用一个例子来看看,冒泡的过程: 4 5 6 3 2 1。

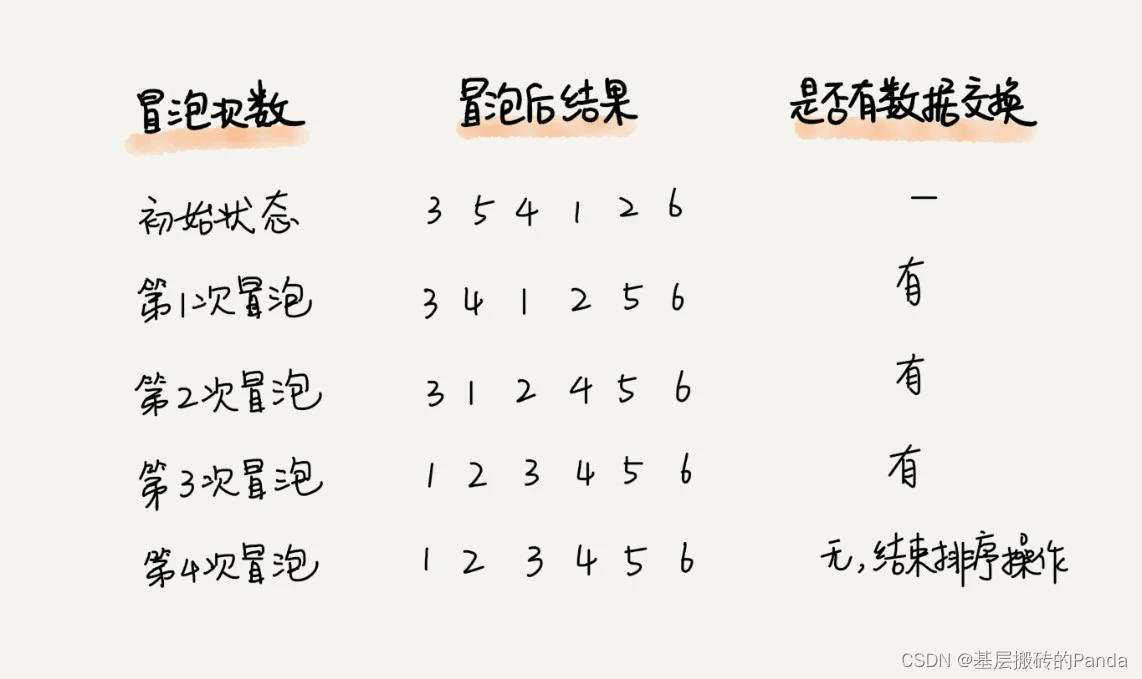
再看一个冒泡优化的例子:3 5 4 1 2 6
// 冒泡排序
void BubbleSort(vector<int>& nums)
{
int size = nums.size();
for (int i = 0; i < size; i++)
{
bool order = false;
for (int j = 0; j < size-i-1; j++)
{
if (nums[j] > nums[j+1]){
order = true;
swap(nums[j], nums[j+1]);
}
}
if (!order){ // 优化,如果在排序中途已经有序了就没必要再继续执行冒泡操作了
break;
}
}
cout << "Bubble Sort: " << endl;
for (int i = 0; i < size; i++){
cout << nums[i] << " " ;
}
cout << endl;
}
小结:
冒泡排序因为是相邻比较,不满足大小调减才会被交换位置,所以是稳定的;不需要开辟空间直接在原数组上操作,所以是原地排序。
最好时间复杂度是O(n),最坏时间复杂度是O(n2)。
2.2 插入排序
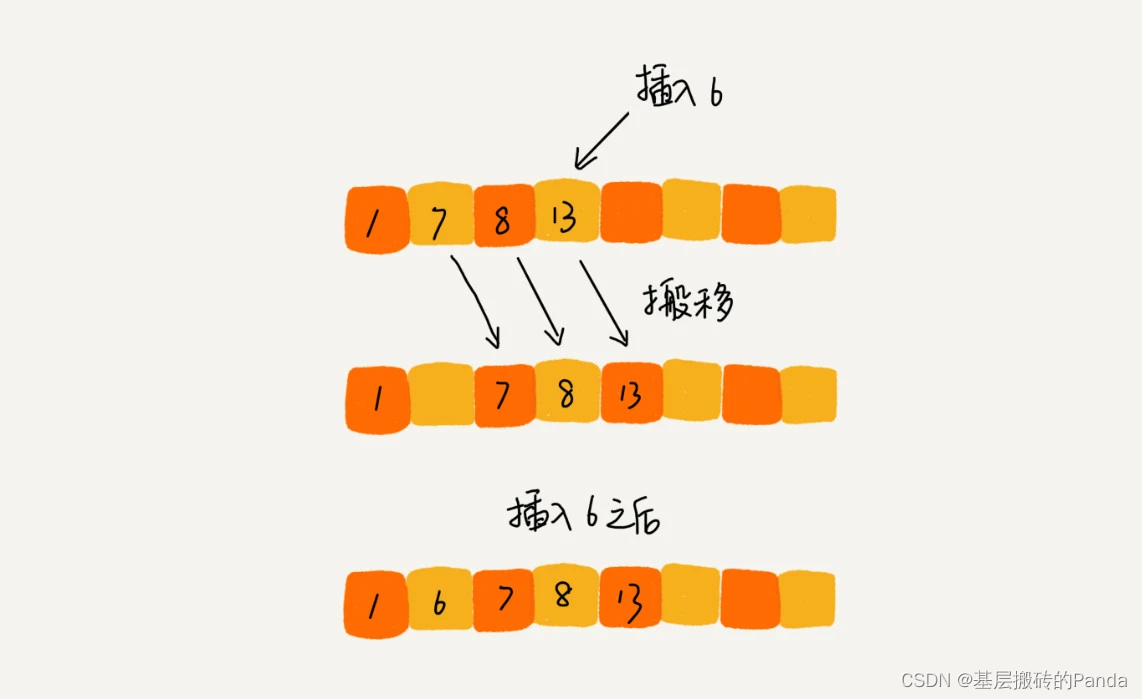
我们先来看一个问题,在一个已经有序的数组中如何保证插入数据后,数组仍然有序。很简单,就是遍历数组找到适当的位置插入即可。
思路:插入排序将数组分为已经有序的部分和乱序的部分。初始有序部分只有第一个元素,然后从乱序部分取元素插入到有序部分的合适位置。
void InserSort(vector<int> &nums){
int n = nums.size();
for (int i = 1; i < n; i++)
{
int tmp = nums[i];
for (int j = i-1; j >= 0; j--){
if (nums[j] > tmp){
nums[j+1] = nums[j];
}
}
nums[j+1] = tmp;
}
}
小结:
插入排序因为是遍历寻找合适位置,所以是稳定的;不需要开辟空间直接在原数组上操作,所以是原地排序。
在数据已经有序的情况下,从第二个元素开始,只需要比一次就能找到插入位置,需要执行n-1次,所以最好时间复杂度是O(n);在数据倒序的情况下最坏时间复杂度是O(n2)。
2.3 选择排序
思路:在插入排序的基础上,每次从乱序部分中找出最小的元素位置的下标,插入到合适的位置。
void CSort::SelectSort(vector<int>& nums){
int size = nums.size();
int min = 0;
for (int i = 0; i < size; i++)
{
min = i;
for (int j = i+1; j < size; j++){
if (nums[j] < nums[min]){
min = j;
}
}
if (min != i){
swap(nums[min], nums[i]);
}
}
cout << "Select Sort: " << endl;
for (int i = 0; i < size; i++){
cout << nums[i] << " " ;
}
cout << endl;
}