代码随想录算法训练营 Day4 | 链表 | LC24. 两两交换链表中的节点、LC19. 删除链表的倒数第 N 个结点、LC面试题 02.07. 链表相交、LC142. 环形链表 II
因为tw面试后有点摆烂,然后又觉得这几题都是之前做过的就耽搁了一天没打卡,今天补上。
LC19. 删除链表的倒数第 N 个结点
题目描述:
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
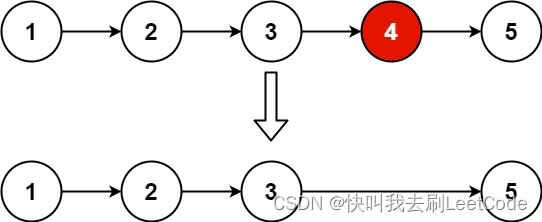
示例 1:
输入:head = [1,2,3,4,5], n = 2
输出:[1,2,3,5]
示例 2:
输入:head = [1], n = 1
输出:[]
示例 3:
输入:head = [1,2], n = 1
输出:[1]
核心思想:
1. 快慢指针,求倒数n个结点只需要让快指针先走n步,然后快慢指针再一起移动,这样当快指针移动到null的时候,慢指针指向的结点就是倒数第n个结点。
2.虚拟头结点:链表题中要学会使用虚拟头结点,这样就可以更方便的不用去特殊处理头结点
3.前驱结点:链表题中,一般需要删除某个结点的时候,我们都需要求该结点的前驱结点,这样才方便操作删除这个步骤。
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummyHead = new ListNode(0);
dummyHead.next = head;
ListNode fast = dummyHead , slow = dummyHead;
n++;//让快指针多走一步,等价于慢指针少走一步,也就是慢指针最终会指向想要删除的结点的前驱结点
while(n-->0 && fast!=null){
fast=fast.next;
}
while(fast!=null){
fast=fast.next;
slow=slow.next;
}
slow.next=slow.next.next;
return dummyHead.next;
}
}
LC24. 两两交换链表中的节点
题目描述:
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
示例 1:
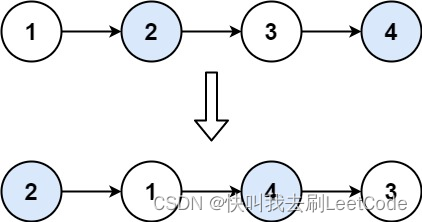
输入:head = [1,2,3,4]
输出:[2,1,4,3]
示例 2:
输入:head = []
输出:[]
示例 3:
输入:head = [1]
输出:[1]
提示:
链表中节点的数目在范围 [0, 100] 内
0 <= Node.val <= 100
画图帮助理解两两交换的核心步骤
注意事项:
1.使用虚拟头结点,可以避免需要特殊处理头结点。
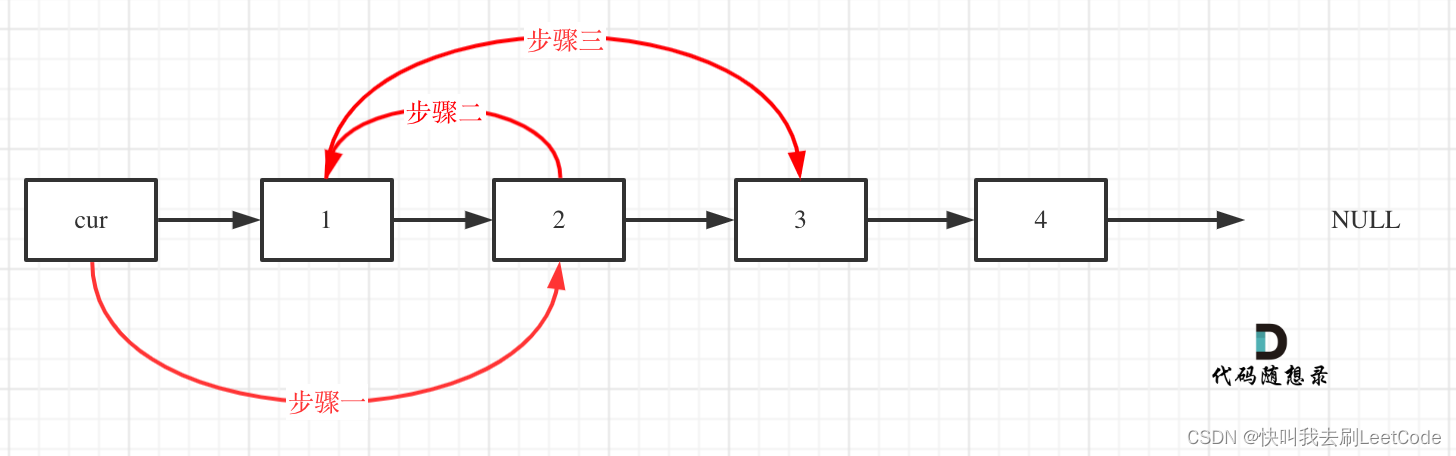
2. 把当前结点指向前一个结点之前,需要先暂存当前节点本来的下一个结点,不然的话就不知道当前结点本来的下一个结点是哪个,两两交换后指针无法继续向后移动。
3. 理解交换逻辑时,如果不画图的话很容易与原结点顺序混淆,比如其实cur->next已经是2了,误以为cur->next仍然为1.
class Solution {
public ListNode swapPairs(ListNode head) {
ListNode dummyHead = new ListNode(0);
dummyHead.next = head;
ListNode cur = dummyHead;
//cur每次都会移动到需要交换结点的一对中的靠右的结点
//如果链表为奇数,cur最终停留在倒数第二个结点。
//如果链表为偶数,cur最终停留再倒数第一个结点。
while(cur.next!=null&&cur.next.next!=null){//&&前后顺序不可以调换,因为要先判断cur.next再判断cur.next.next
ListNode pre = cur.next;//存第一个结点
cur.next=cur.next.next;//dummy指向第二个结点
ListNode temp = cur.next.next;//暂存第三个结点
cur.next.next =pre;//第二个结点指向第一个结点
pre.next=temp;//第一个结点指向第三个节点
cur=cur.next.next;//向后移动两个结点
}
return dummyHead.next;
}
}
LC面试题 02.07. 链表相交
题目描述:
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点,返回 null 。
图示两个链表在节点 c1 开始相交:
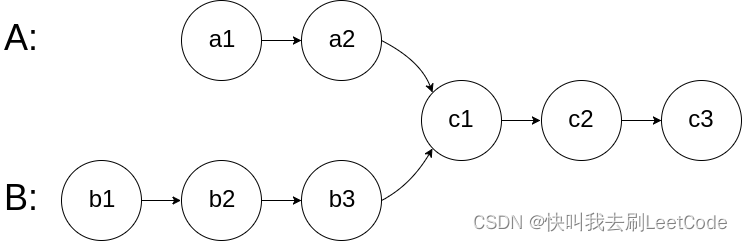
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
示例 1:
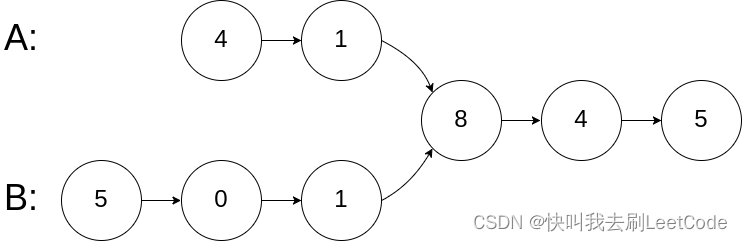
输入:ntersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出:Intersected at ‘8’
解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。
在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
示例 2:
输入:intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Intersected at ‘2’
解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [0,9,1,2,4],链表 B 为 [3,2,4]。
在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
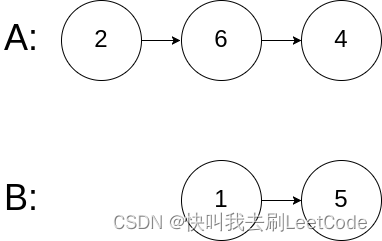
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:null
解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。
由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
这两个链表不相交,因此返回 null 。
提示:
listA 中节点数目为 m
listB 中节点数目为 n
0 <= m, n <= 3 * 104
1 <= Node.val <= 105
0 <= skipA <= m
0 <= skipB <= n
如果 listA 和 listB 没有交点,intersectVal 为 0
如果 listA 和 listB 有交点,intersectVal == listA[skipA + 1] == listB[skipB + 1]
进阶:你能否设计一个时间复杂度 O(n) 、仅用 O(1) 内存的解决方案?
两层循环遍历的方法都很容易想到,这里主要说时间复杂度为O(n)的解法
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
int size1=0 , size2 =0;
int num = 0;
ListNode fast = headA ,slow = headB;
while(headA!=null){
//虽然是向后移动一次size才加一,即当移动到第二个结点时size才为1
//但while结束的条件是headA!=null,最后一次循环时会把移动到null结点的那次也加一,所以得到的结果确实是size
headA=headA.next;
size1++;
}
while(headB!=null){
headB=headB.next;
size2++;
}
if(size1<size2){//注意这里不能想当然的就直接fast=headB ,slow=headA这样,因为上面两次while循环后,headA和headB都为null了
ListNode temp = fast;
fast = slow;
slow = temp;
}
num = Math.abs(size1-size2);
while(num-->0){
fast=fast.next;
}
while(fast!=null&&slow!=null){
if(fast==slow) {
return fast;
}
fast=fast.next;
slow=slow.next;
}
return null;
}
}
142. 环形链表 II
题目描述:
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1:
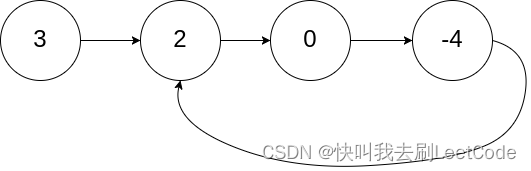
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
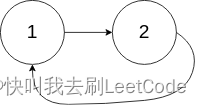
输入:head = [1,2], pos = 0
输出:返回索引为 0 的链表节点
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:

输入:head = [1], pos = -1
输出:返回 null
解释:链表中没有环。
提示:
链表中节点的数目范围在范围 [0, 104] 内
-105 <= Node.val <= 105
pos 的值为 -1 或者链表中的一个有效索引
进阶:你是否可以使用 O(1) 空间解决此题?
核心思想:
1. 如何判断链表是否有环:
想象一个场景,两个人在一个跑道上跑步,一个人跑的比另一个人快,是不是跑的快的人总会追上跑得慢的人,这其实就是一个数学里的追及问题。所以判断链表是否有环,就可以用快慢指针,只要快指针追上了慢指针就代表链表有环。
2. 如何判断环的入口:
这里需要画图来方便理解:
图来自力扣题解
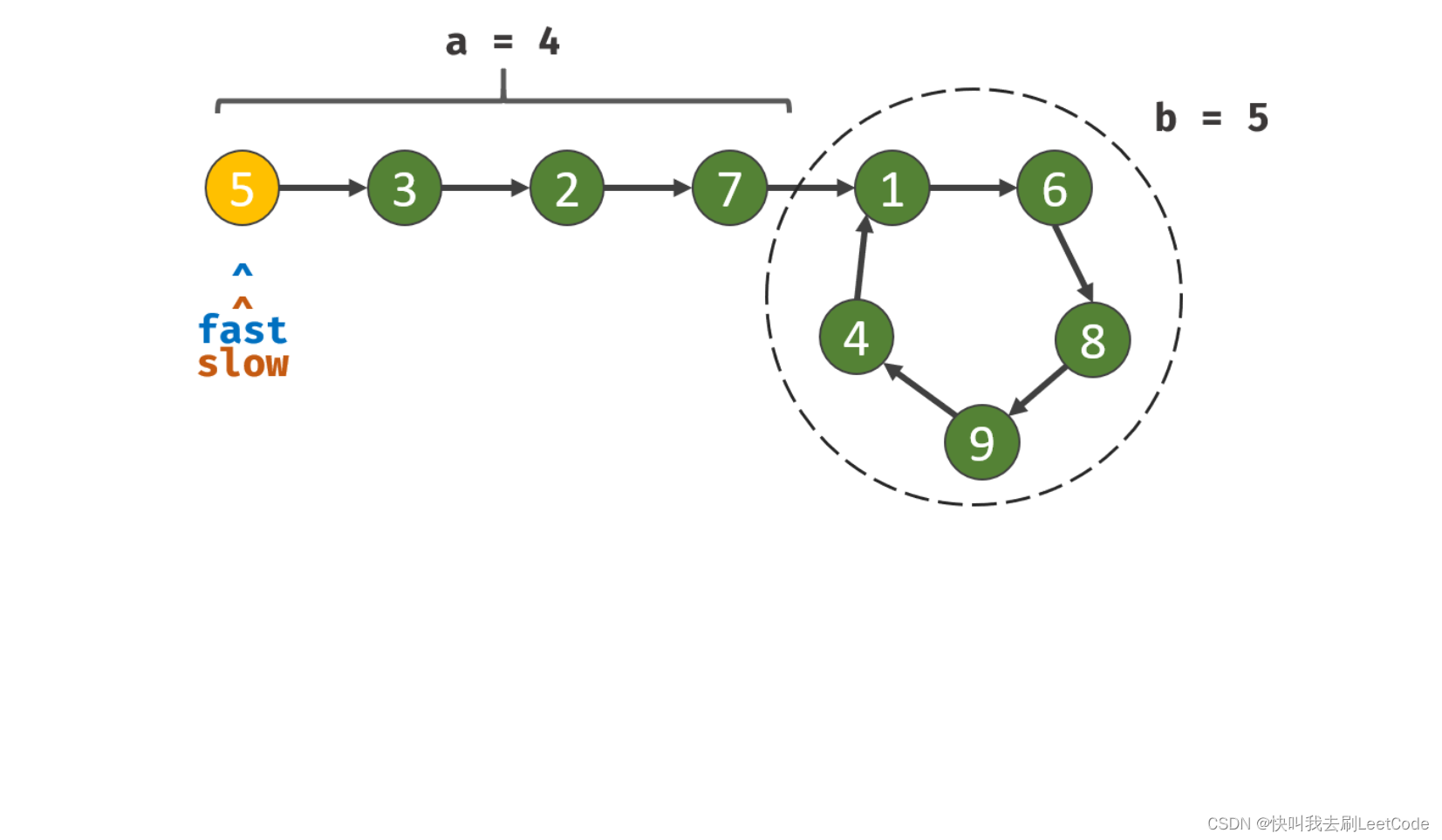
我们设入环前的直线长度为a,环的长度为b,定义一个快指针它每次走两步,一个慢指针每次走一步
根据这个条件我们可以推理出以下结论:
- fast走过的距离 = slow走过距离 * 2
- fast走过的距离 = slow走过的距离+nb(fast一定会比slow多走n个环的距离)
上面两式相减得:
- slow走过的距离 = nb
再根据图我们可以知道,无论是快指针还是慢指针,当他们在环中绕n圈后最终走到环的入口时,他们走过的距离一定为:
- a + nb
所以当快慢指针相遇的时候,无论他们相遇在环中的哪个点,此时slow走过的距离一定为nb,而走到环的入口的总距离为a + nb 也就是说它只需要再走a个距离就能走到环的入口了,那么怎么知道a的距离为多少呢?,还记得我们最开始设的条件就是从头结点到环的入口的直线距离为a吗?,那么此时只需要再让一个指针ptr从头节点出发,ptr和slow的移动速度保持一致,slow走了多少步,ptr就走多少步。此时就把求a的距离为多少这个问题转换成了判断ptr和slow是否相遇的问题,总结一下:
- slow再走a步,它就会到达环的入口。
- ptr是从头结点出发的,头结点到环的入口距离为a,也就是ptr再走a步也会到达环的入口。
- 即当slow和ptr再次相遇时,相遇的位置就是环的入口。
综上所述,解题步骤为:
- 定义快指针每次走两步,慢指针每次走一步。
- 当他们相遇时,表示有环。
- 相遇后再定义一个指针ptr从头结点出发,保持速度和slow一样,ptr和slow再次相遇时为环的入口。
public class Solution {
public ListNode detectCycle(ListNode head) {
ListNode fast = head, slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) {
ListNode ptr = head;
while (ptr != slow) {
ptr = ptr.next;
slow = slow.next;
}
return ptr;
}
}
return null;
}
}