一、算法原理
插入排序属于稳定排序法,是一种常用的排序算法。直接插入排序算法可以利用静态数组来实现,也可以使用静态链表或者单链表来实现。本文给出了直接插入算法的静态链表实现方法,即表插入排序算法。
基于静态链表实现直接插入排序,就是把待排序的数组放入静态链表中,通过修改静态链表中的索引域的值来给出排序结果。该排序方法不改变原数组中元素的位置,只是在索引域中给出其在排序表中位置,因此相比较于直接插入排序算法,本算法不需要移动元素。
下面例子演示了使用单表插入排序算法的过程。
Demo:
假设一组散乱数据:{ 40,30,50,10,20 }
Step 0:创建静态链表,元素0不存储元素,其“Next下标”项表示当前静态链表中最小元素的下标

Step 1:将元素40存入静态链表下标为1的位置,当前静态链表中最小元素是40,其下标是1,所以元素0的“Next下标”赋值为1,而元素1的“Next下标”值为0,表示其为当前静态数组的最后一个元素。
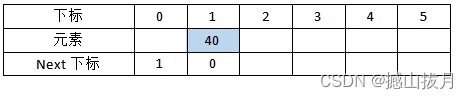
Step 2:将元素30存入静态链表下标为2的位置,当前静态链表中最小元素是30,因此修改元素0的“Next下标”为2,修改元素2的“Next下标”为1。
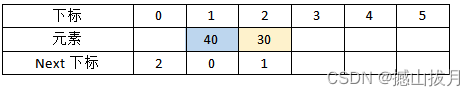
Step 3:将元素50存入静态链表下标为3的位置,当前静态链表中最小元素是30,最大元素是50,因此修改“Next下标”值如下表所示。
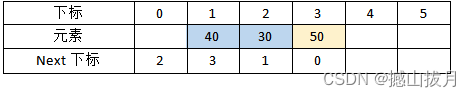
Step 4:将元素10存入静态链表下标为4的位置,当前静态链表中最小元素是10,因此修改元素0的“Next下标”值为4,其它元素的“Next下标”值如下表所示。
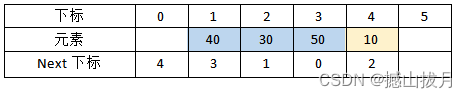
Step 5:将元素20存入静态链表下标为5的位置,各元素的“Next下标”值如下表所示。
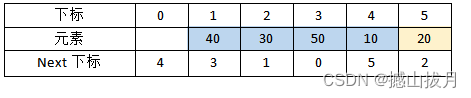
在这一步中插入元素20时,其是当前静态链表中第二小的元素,因此此处修改其下标及最小元素10的下标时,需要单独处理,也就是需要记录比元素20小的相邻的那个元素的位置,然后将其“Next下标”值赋值为第二小的下标。
二、基于表插入排序算法的C程序
1. 表插入排序算法函数
void TableInsertSort( Table arr[], int length )
{
int i, k ,loc;
arr[0].nextInd = 1;
arr[1].nextInd = 0;
for( i = 2; i <= length; i++ )
{
k = loc = 0;
while( 1 )
{
if( arr[i].data <= arr[ arr[k].nextInd ].data )
{
if( k == 0 )
{
loc = 0;
}
arr[i].nextInd = arr[loc].nextInd;
arr[loc].nextInd = i;
break;
}
else
{
if( arr[ arr[k].nextInd ].nextInd == 0 )
{
arr[ arr[k].nextInd ].nextInd = i;
arr[i].nextInd = 0;
break;
}
loc = arr[k].nextInd;//记录比当前元素小的元素下标
k = arr[ arr[k].nextInd ].nextInd;
}
}
}
}
2.测试代码(仅供参考)
//直接插入排序算法之静态链表实现方法
#include"stdio.h"
typedef struct tbl
{
int data;
int nextInd;
}Table;
void TableInsertSort( Table arr[], int length );
int main()
{
int i;
int a[] = { 4, 3, 5, 1, 2 };
Table arr[6];
int length = 5;
for( i = 1; i <= length; i++ )
{
arr[i].data = a[i-1];
arr[i].nextInd = 0;
}
arr[0].data = 0;
TableInsertSort( arr, length );
printf( "index :" );
for( i = 0; i <= length; i++ )
{
printf( "%5d", i );
}
printf( "\n" );
printf( "data :" );
for( i = 0; i <= length; i++ )
{
printf( "%5d", arr[i].data );
}
printf( "\n" );
printf( "nextInd:" );
for( i = 0; i <= length; i++ )
{
printf( "%5d", arr[i].nextInd );
}
printf( "\n" );
return 0;
}
void TableInsertSort( Table arr[], int length )
{
int i, k ,loc;
arr[0].nextInd = 1;
arr[1].nextInd = 0;
for( i = 2; i <= length; i++ )
{
k = loc = 0;
while( 1 )
{
if( arr[i].data <= arr[ arr[k].nextInd ].data )
{
if( k == 0 )
{
loc = 0;
}
arr[i].nextInd = arr[loc].nextInd;
arr[loc].nextInd = i;
break;
}
else
{
if( arr[ arr[k].nextInd ].nextInd == 0 )
{
arr[ arr[k].nextInd ].nextInd = i;
arr[i].nextInd = 0;
break;
}
loc = arr[k].nextInd;//记录比当前元素小的元素下标
k = arr[ arr[k].nextInd ].nextInd;
}
}
}
}
3.运行结果
