题目
题干
设计链表的实现。您可以选择使用单链表或双链表。单链表中的节点应该具有两个属性:val 和 next。val 是当前节点的值,next 是指向下一个节点的指针/引用。如果要使用双向链表,则还需要一个属性 prev 以指示链表中的上一个节点。假设链表中的所有节点都是 0-index 的。
在链表类中实现这些功能:
get(index):获取链表中第 index 个节点的值。如果索引无效,则返回-1。
addAtHead(val):在链表的第一个元素之前添加一个值为 val 的节点。插入后,新节点将成为链表的第一个节点。
addAtTail(val):将值为 val 的节点追加到链表的最后一个元素。
addAtIndex(index,val):在链表中的第 index 个节点之前添加值为 val 的节点。如果 index 等于链表的长度,则该节点将附加到链表的末尾。如果 index 大于链表长度,则不会插入节点。如果index小于0,则在头部插入节点。
deleteAtIndex(index):如果索引 index 有效,则删除链表中的第 index 个节点。
示例:
MyLinkedList linkedList = new MyLinkedList();
linkedList.addAtHead(1);
linkedList.addAtTail(3);
linkedList.addAtIndex(1,2); //链表变为1-> 2-> 3
linkedList.get(1); //返回2
linkedList.deleteAtIndex(1); //现在链表是1-> 3
linkedList.get(1); //返回3
提示:
所有val值都在 [1, 1000] 之内。
操作次数将在 [1, 1000] 之内。
请不要使用内置的 LinkedList 库。
解法
方法一:单向链表
思路
实现单向链表,即每个节点仅存储本身的值和后继节点。除此之外,我们还需要一个哨兵(sentinel)节点作为头节点,和一个size 参数保存有效节点数。如下图所示。
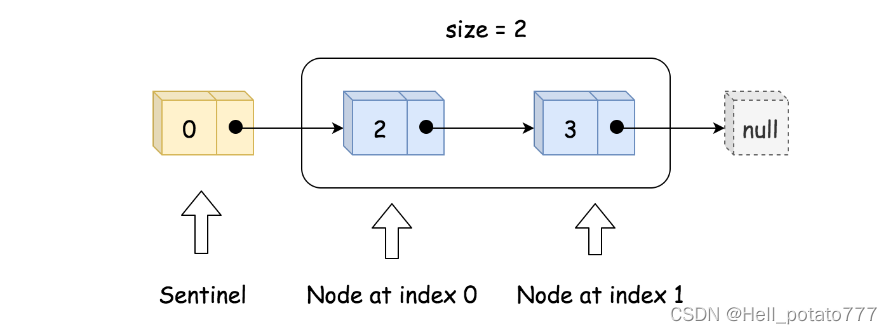
初始化时,只需创建头节点head 和 size 即可。
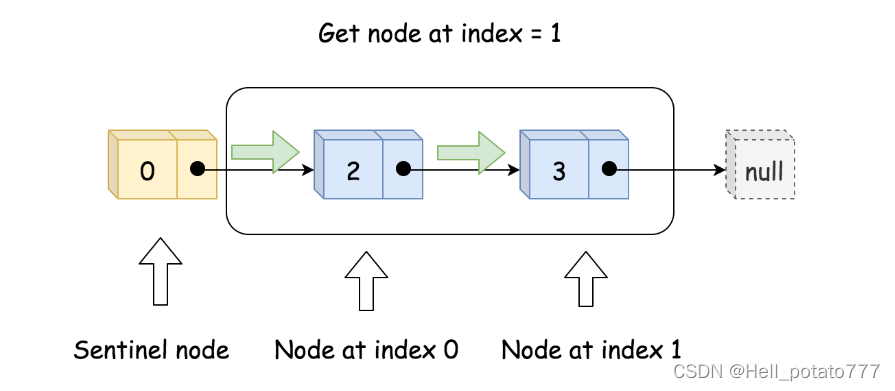
实现get(index) 时,先判断有效性,再通过循环来找到对应的节点的值。如下图所示。
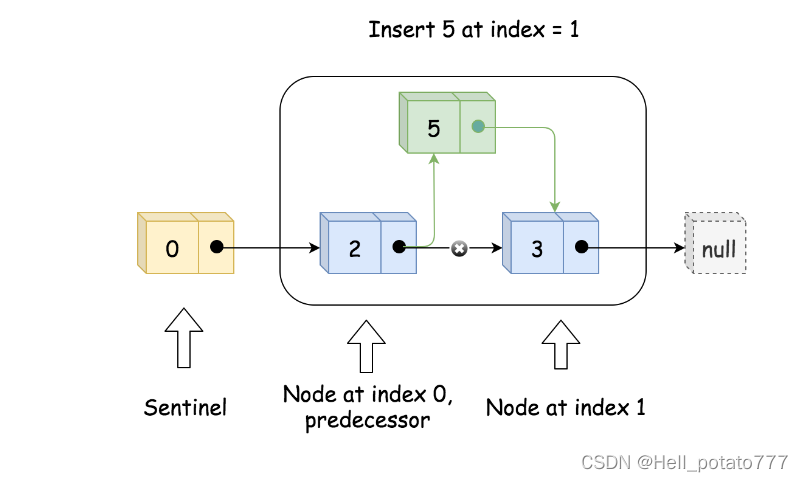
实现addAtIndex(index, val) 时,如果 index 是有效值,则需要找到原来下标为 index 的节点的前驱节点 pred,并创建新节点to_add,将to_add 的后继节点设为 pred 的后继节点,将 pred 的后继节点更新为to_add,这样就将to_add 插入到了链表中。最后需要更新 size。这样的操作对于index=0 也成立,如以下两张图所示。
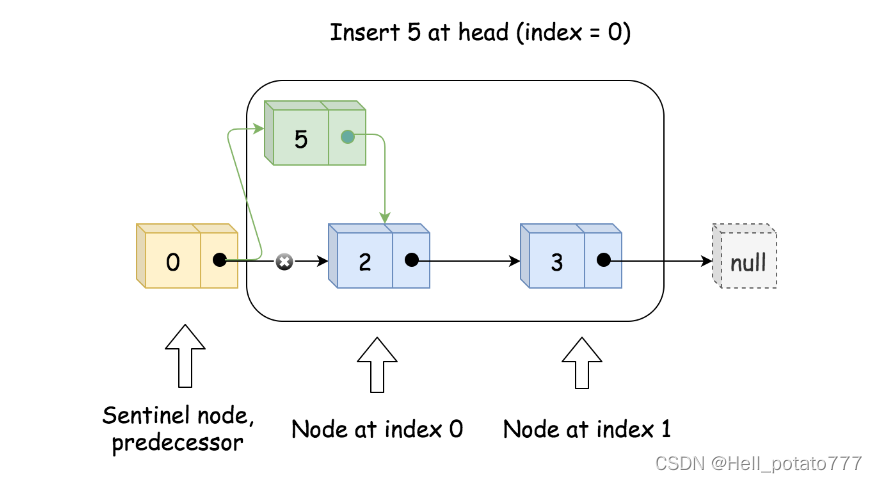
实现addAtHead(val) 和 addAtTail(val) 时,可以借助addAtIndex(index, val) 来实现。
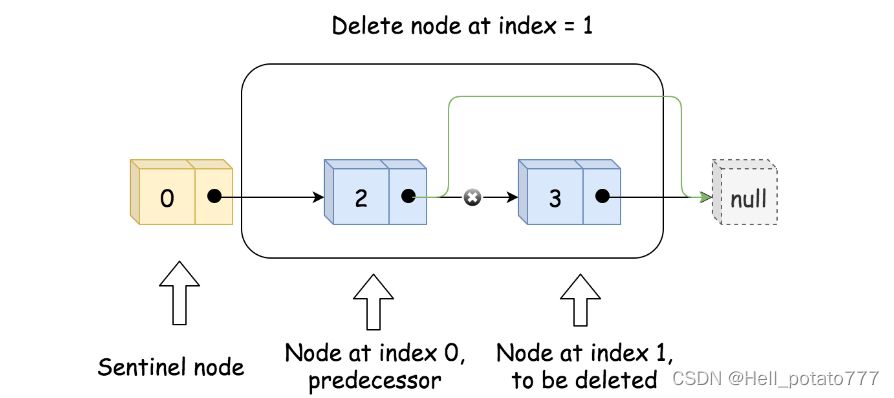
实现deleteAtIndex(index),先判断参数有效性。然后找到下标为index 的节点的前驱节点 pred,通过将 pred 的后继节点更新为pred 的后继节点的后继节点,来达到删除节点的效果。同时也要更新size。如下图所示。
class MyLinkedList {
int size;
ListNode head;
public MyLinkedList() {
size = 0;
head = new ListNode(0);
}
public int get(int index) {
if (index < 0 || index >= size) {
return -1;
}
ListNode cur = head;
for (int i = 0; i <= index; i++) {
cur = cur.next;
}
return cur.val;
}
public void addAtHead(int val) {
addAtIndex(0, val);
}
public void addAtTail(int val) {
addAtIndex(size, val);
}
public void addAtIndex(int index, int val) {
if (index > size) {
return;
}
index = Math.max(0, index);
size++;
ListNode pred = head;
for (int i = 0; i < index; i++) {
pred = pred.next;
}
ListNode toAdd = new ListNode(val);
toAdd.next = pred.next;
pred.next = toAdd;
}
public void deleteAtIndex(int index) {
if (index < 0 || index >= size) {
return;
}
size--;
ListNode pred = head;
for (int i = 0; i < index; i++) {
pred = pred.next;
}
pred.next = pred.next.next;
}
}
class ListNode {
int val;
ListNode next;
public ListNode(int val) {
this.val = val;
}
}
复杂度分析
时间复杂度:初始化消耗 O(1),get 消耗 O(index),addAtHead 消耗 O(1),addAtTail 消耗 O(n),其中 n 为链表当前长度,即 addAtHead,addAtTail 和 addAtIndex 已调用次数之和,addAtIndex 消耗O(index)。
空间复杂度:所有函数的单次调用空间复杂度均为 O(1),总体空间复杂度为O(n),其中 n为 addAtHead,addAtTail 和 addAtIndex 调用次数之和。
方法二:双向链表
思路
实现双向链表,即每个节点要存储本身的值,后继节点和前驱节点。除此之外,需要一个哨兵节点作为头节点head 和一个哨兵节点作为尾节点tail。仍需要一个 size 参数保存有效节点数。如下图所示。
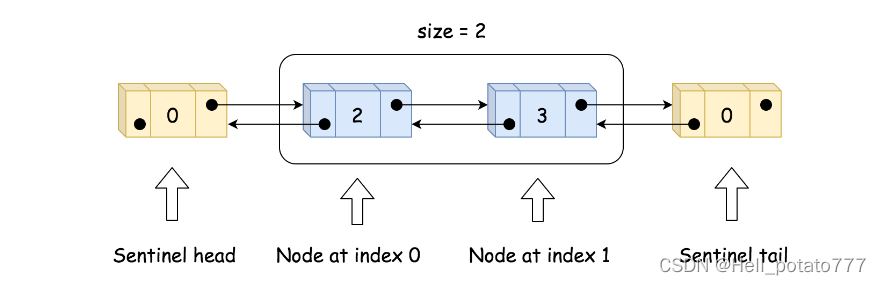
初始化时,只需创建头节点 head 和 size 即可。
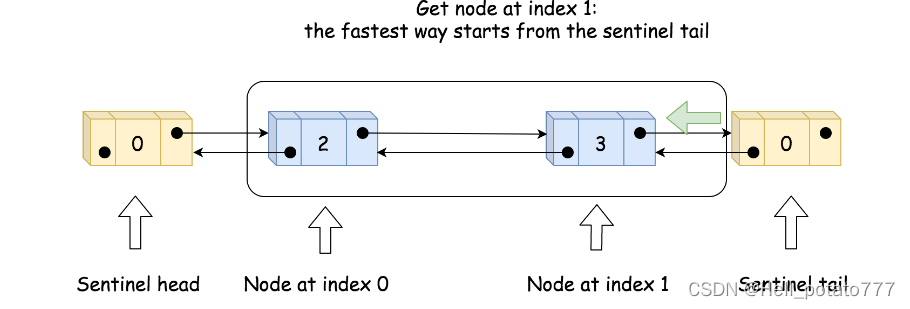
实现 get(index) 时,先判断有效性,然后再比较从head 还是 tail 来遍历会比较快找到目标,然后进行遍历。如下图所示。
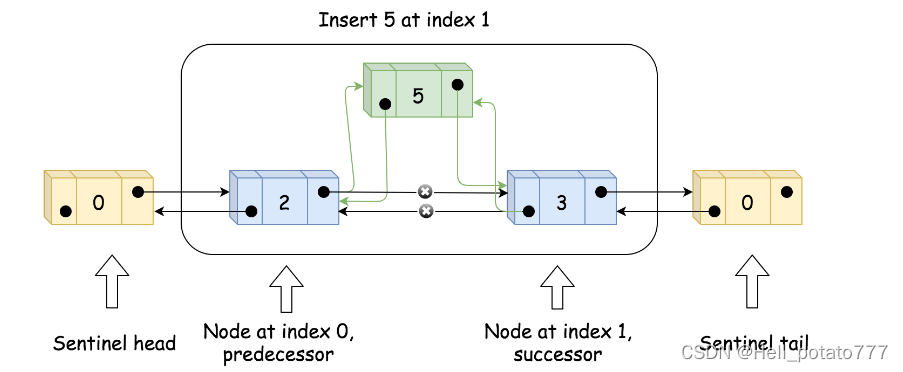
实现addAtIndex(index, val) 时,如果index 是有效值,则需要找到原来下标为 index 的节点 succ 和前驱节点 pred,并创建新节点to_add,再通过各自 prev 和next 变量的更新来增加to_add。最后需要更新 size。如以下两张图所示。
实现 addAtHead(val) 和addAtTail(val) 时,可以借助 addAtIndex(index, val) 来实现。
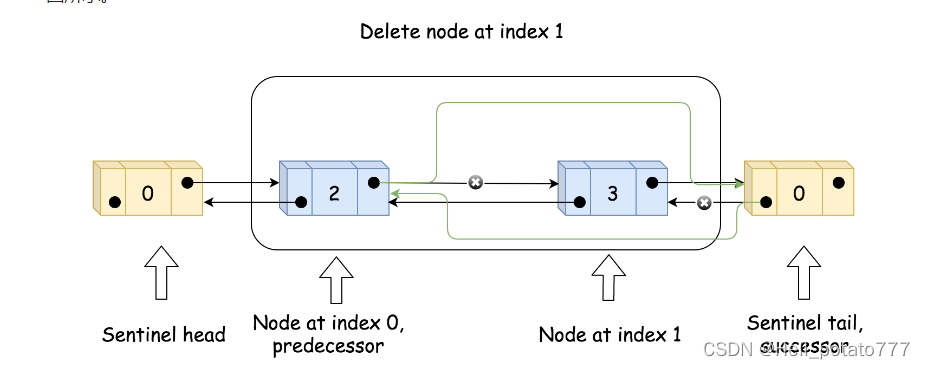
实现deleteAtIndex(index),先判断参数有效性。然后找到下标为index 的节点的前驱节点 pred 和后继节点 succ,再通过各自prev 和 next 变量的更新来删除节点,来达到删除节点的效果。同时也要更新size。如下图所示。
class MyLinkedList {
int size;
ListNode head;
ListNode tail;
public MyLinkedList() {
size = 0;
head = new ListNode(0);
tail = new ListNode(0);
head.next = tail;
tail.prev = head;
}
public int get(int index) {
if (index < 0 || index >= size) {
return -1;
}
ListNode curr;
if (index + 1 < size - index) {
curr = head;
for (int i = 0; i <= index; i++) {
curr = curr.next;
}
} else {
curr = tail;
for (int i = 0; i < size - index; i++) {
curr = curr.prev;
}
}
return curr.val;
}
public void addAtHead(int val) {
addAtIndex(0, val);
}
public void addAtTail(int val) {
addAtIndex(size, val);
}
public void addAtIndex(int index, int val) {
if (index > size) {
return;
}
index = Math.max(0, index);
ListNode pred, succ;
if (index < size - index) {
pred = head;
for (int i = 0; i < index; i++) {
pred = pred.next;
}
succ = pred.next;
} else {
succ = tail;
for (int i = 0; i < size - index; i++) {
succ = succ.prev;
}
pred = succ.prev;
}
size++;
ListNode toAdd = new ListNode(val);
toAdd.prev = pred;
toAdd.next = succ;
pred.next = toAdd;
succ.prev = toAdd;
}
public void deleteAtIndex(int index) {
if (index < 0 || index >= size) {
return;
}
ListNode pred, succ;
if (index < size - index) {
pred = head;
for (int i = 0; i < index; i++) {
pred = pred.next;
}
succ = pred.next.next;
} else {
succ = tail;
for (int i = 0; i < size - index - 1; i++) {
succ = succ.prev;
}
pred = succ.prev.prev;
}
size--;
pred.next = succ;
succ.prev = pred;
}
}
class ListNode {
int val;
ListNode next;
ListNode prev;
public ListNode(int val) {
this.val = val;
}
}
复杂度分析
时间复杂度:初始化消耗 O(1),get 消耗 O(index),addAtHead 消耗 O(1),addAtTail 消耗 O(1),addAtIndex 消耗O(index)。
空间复杂度:所有函数单次调用的空间复杂度均为 O(1),总体空间复杂度为 O(n),其中 n 为addAtHead,addAtTail 和 addAtIndex 调用次数之和。