[数据结构与算法]数据结构题目收录（十）

1、下列关于广度优先算法的说法中，正确的是（）。

Ⅰ.当各边的权值相等时，广度优先算法可以解决单源最短路径问题
Ⅱ.当个边的权值不等时，广度优先算法可用来解决单源最短路径问题
Ⅲ.广度优先遍历算法类似于树中的后序遍历算法
Ⅳ.实现图的广度优先算法时，使用的数据结构是队列

• A：Ⅰ、Ⅳ
• B：Ⅱ、Ⅲ、Ⅳ
• C：Ⅱ、Ⅳ
• D：Ⅰ、Ⅲ、Ⅳ

解析

广度优先搜索以起始结点为中心，一层一层地向外层扩展遍历图的顶点，因此无法考虑到边权值，只适合求边权值相等的图的单源最短路径。广度优先搜索相当于树的层序遍历，Ⅲ错误。广度优先搜索需要用到队列，深度优先搜索需要用到栈，Ⅳ正确。

答案：A

2、对一个有n个顶点、e条边的图采用邻接表表示时，进行DFS遍历的时间复杂度为（），空间复杂度为（）；进行BFS遍历的时间复杂度为（），空间复杂度为（）。

• A：O(n)
• B：O(e)
• C：O(n+e)
• D：O(1)

解析

深度优先遍历时，每个顶点表结点和每个边表结点均查找一次，每个顶点递归调用一次，需要借助一个递归工作栈；
广度优先遍历时，也是每个顶点表结点和每个边表结点均查找一次，每个顶点进入队列一次。
所以都是选C，A。

答案：C、A、C、A

3、对一个有n个顶点、e条边的图采用邻接矩阵表示时，进行DFS遍历的时间复杂度为（），进行BFS遍历的时间复杂度为（）。

• A：$O(n^2)$
• B：O(e)
• C：O(n+e)
• D：$O(e^2)$

解析

采用邻接矩阵表示时，查找一个顶点所有出边的时间复杂度为O(n)，共有n个顶点，故时间复杂度均为O($n^2$)。

答案：A、A

4、如下图所示，在下面的5个序列中，符合深度优先遍历的序列个数是（）

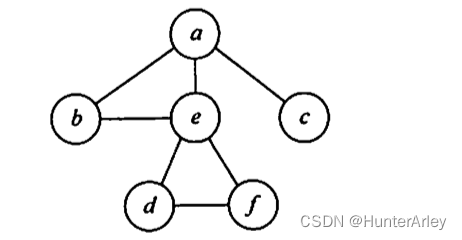
1. aebfdc
2. acfdeb
3. aedfcb
4. aefdbc
5. aecfdb

• A：5
• B：4
• C：3
• D：2

解析

仅1和4正确。
以2为例，遍历到c之后，与c邻接且未被访问的结点为空集，所以应为a的邻接点b或e入栈。
以3为例，因为遍历要按栈退回，所以是先b后c，而不能先c后b。

答案：D

5、用邻接表存储的图的深度优先遍历算法类似于树的（），而其广度优先遍历算法类似于树的（）。

• A：中序遍历
• B：先序遍历
• C：后序遍历
• D：按层次遍历

解析

图的深度优先搜索类似于树的先根遍历，即先访问结点，再递归向外层结点遍历，都采用回溯算法。
图的广度优先搜索类似于树的层序遍历，即一层一层向外层扩展遍历，都需要采用队列来辅助算法的实现。

答案：B、D

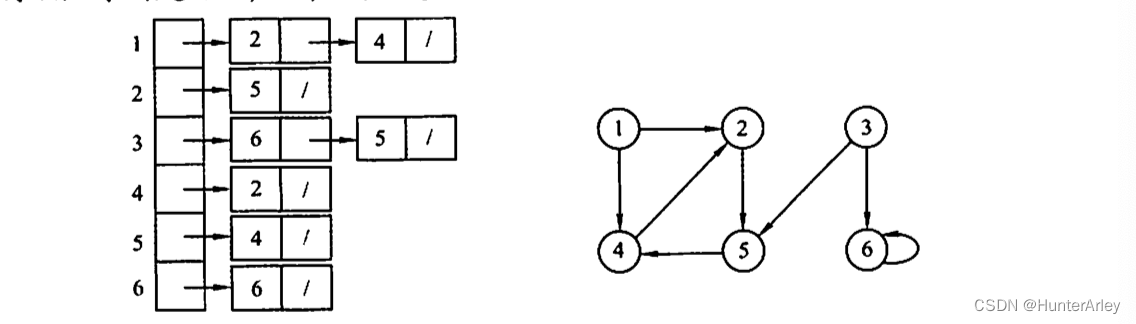
6、一个有向图G的邻接表存储如下图所示，从顶点1出发，对图G调用深度优先遍历所得顶点序列是（）；按广度优先遍历所得顶点序列是（）。

• A：125436
• B：124536
• C：124563
• D：362514

解析

DFS（深度优先遍历）序列产生的路径为<1,2>，<2,5>，<5,4>，??,6>；
BFS（广度优先遍历）序列产生的路径为<1,2>，<1,4>，<2,5>，??,6>。

答案：A、B

7、使用DFS算法递归地遍历一个无环有向图，并在退出递归时输出相应顶点，这样得到的顶点序列是（）。

• A：逆拓扑有序
• B：拓扑有序
• C：无序的
• D：都不是

解析

对一个有向图做深度优先遍历，并未专门判断有向图是否有环（有向回路）存在，无论图中是否有环，都得到一个顶点序列。若无环，在退出递归过程中输出的应是逆拓扑有序序列。
对有向无环图利用深度优先搜索进行拓扑排序的例子如下：如下图所示，退出DFS（深度优先遍历）栈的顺序为efgdcahb，此图的一个拓扑序列为bhacdgfe。该方法的每一步均是先输出当前无后继的结点，即对每个结点v，先递归地求出v的每个后继的拓扑序列。对于一个AOV（）网，按此方法输出的序列是一个逆拓扑序列。

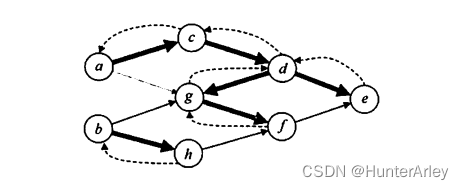
答案：A

8、设无向图G=（V，E）和G’=(V’,E’)，若G’是G的生成树，则下列说法中错误的是（）。

• A：G’为G的子图
• B：G’为G的连通分量
• C：G’为G的极小连通子图且V=V’
• D：G’是G的一个无环子图

解析

连通分量是无向图的极大连通子图，其中极大的含义是将依附于连通分量中顶点的所有边都加上，所以连通分量中可能存在回路，这样就不是生成树了。

注意：极大连通子图是无向图（不一定连通）的连通分量，极小连通子图是连通无向图的生成树。极小和极大是在满足连通的前提下，针对边的数目而言的。极大连通子图包含连通分量的全部边；极小连通子图（生成树）包含连通图的全部顶点，且使其连通的边数最少。

答案：B

9、对有n个顶点、e条边且使用邻接表存储的有向图进行广度优先遍历，其算法的时间复杂度是（）。

• A：O(n)
• B：O(e)
• C：O(n+e)
• D：O(ne)

解析

广度优先遍历需要借助队列实现。采用邻接表存储方式对图进行广度优先遍历时，每个顶点均需入队一次（顶点表遍历），故时间复杂度为O(n)，在搜索所有顶点的邻接点的过程中，每条边至少访问一次（出边表遍历），所以时间复杂度为O(e)，算法总的时间复杂度为O(n+e)。

答案：C

10、平均查找速度而言，下列几种查找速度从慢至快的关系是____。

• A：顺序 折半 哈希 分块
• B：顺序 分块 折半 哈希
• C：分块 折半 哈希 顺序
• D：顺序 哈希 分块 折半

解析

顺序查找的时间复杂度为$O(n)$
分块查找的时间复杂度为$O(lo{g}_{2}n)$到O(n)之间
二分查找的时间复杂度为$O(lo{g}_{2}n)$
哈希查找的时间复杂度为O(1)

答案：B