【LeetCode 310】 310. Minimum Height Trees题解(记忆化搜索)
题目
一棵树以任意一结点为根都可以形成一棵树,找出形成树高度最小的所有根节点。看似 O ( n 2 ) O(n^2) O(n2)能过,实际上过不了,得考虑 O ( n ? log ? n O(n\cdot \log{n} O(n?logn或者 O ( n ) O(n) O(n)的思路。
解题思路
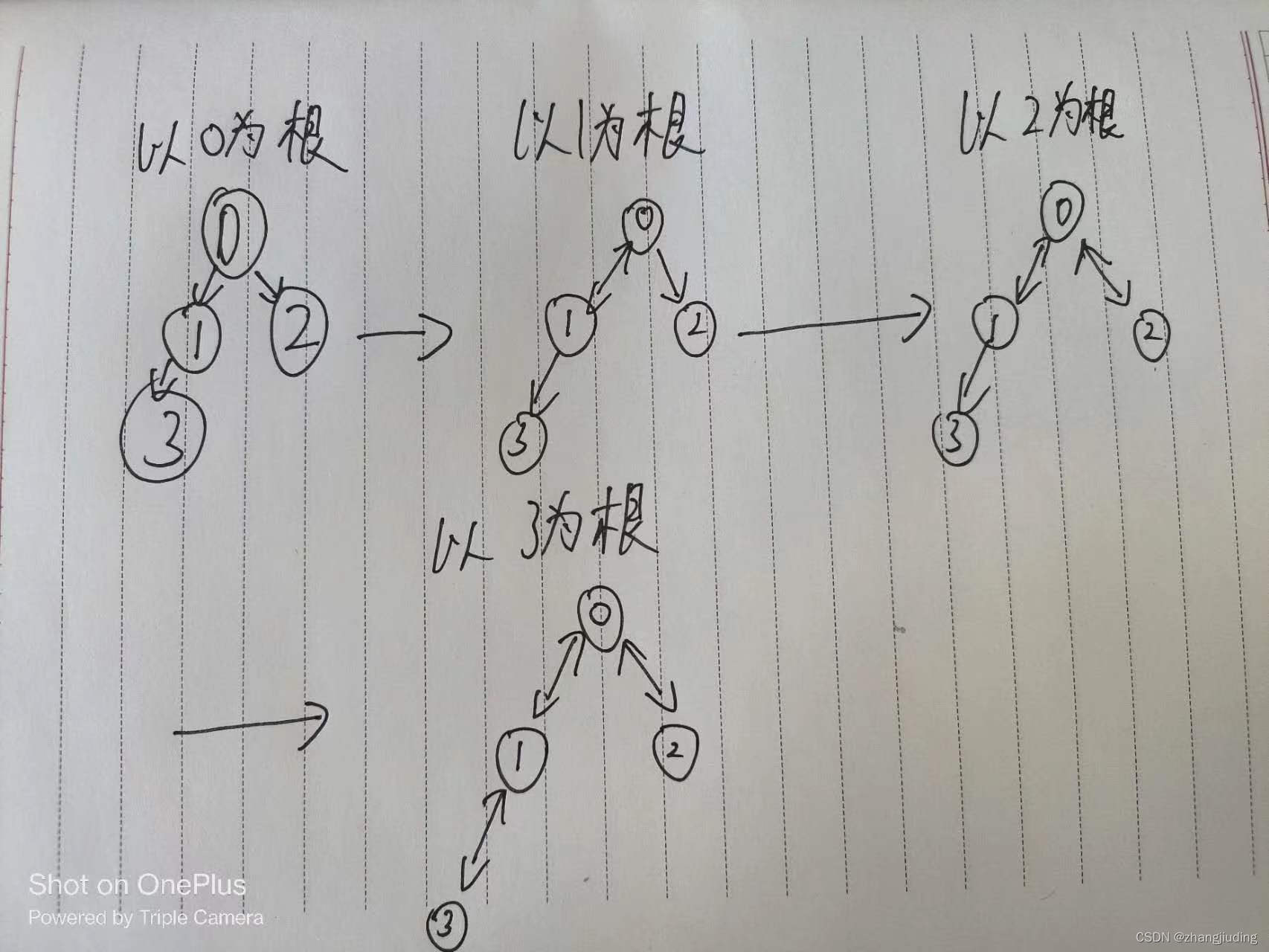
- 假设以结点 x x x为根, x x x有 i ? ? ? j i···j i???j若干子结点,若干子节点为根形成的树高度依次为 H i ? ? ? H j H_i···H_j Hi????Hj?。
- 则以 x x x为根的树的高度为所有子节点最大高度+1= m a x ( H i , ? ? ? , H j ) + 1 max(H_i,···,H_j)+1 max(Hi?,???,Hj?)+1。
- 对于任何一个结点,其子节点方向一旦搜索过则可以直接获取存储的高度而不用再次搜索。(记忆化搜索)
- 所以达到任何一个结点能够
O
(
1
)
O(1)
O(1)获取到其所有子节点的高度,即计算出任何一个结点为根的高度,只需要每条边双向都遍历一遍,遍历次数为
2
?
n
2\cdot n
2?n,时间复杂度为
O
(
n
)
O(n)
O(n)。
Code
class Solution {
public:
// 已经计算过的根节点的树的最小高度。
int minHeight = INT_MAX;
// 记录以其为根使树高度最小的结点。
vector<int> ans;
// dfs深度优先搜索。
// v[i][j].first表示结点i的第j个子结点,v[i][j].second表示结点i到结点v[i][j]方向的深(高)度。
// visit标识当前轮是否访问过某结点。
int dfs(int n, vector<pair<int,int>> v[], int pre, bool* visit){
// 访问过,将当前结点pre的visit设置为true
visit[pre] = true;
// 度为1的树高度为1
int height = 1;
for(int i = 0;i < v[pre].size(); ++i){
// nxt=与pre邻接的第i个结点的值
int nxt = v[pre][i].first;
// 如果pre->nxt方向没访问过,且nxt结点没访问过,则访问nxt结点
if(v[pre][i].second == INT_MAX and !visit[nxt]){
v[pre][i].second = dfs(n,v,nxt,visit)+1;
height = max(height,v[pre][i].second);
// 如果pre->nxt方向访问过,但是当前轮nxt结点没访问过,则从nxt方向获取其最大高度(排除nxt->pre方向)
}else if(!visit[nxt]){
for(int j = 0;j < v[nxt].size(); ++j){
if(v[nxt][j].first != pre){
v[pre][i].second = max(v[pre][i].second,v[nxt][j].second+1);
height = max(height,v[pre][i].second);
}
}
// 如果nxt结点度为1,即只有nxt->pre方向,则将pre->nxt方向深度记为2
if(v[nxt].size() == 1){
v[pre][i].second = 2;
height = max(height,v[pre][i].second);
}
// 如果当前结点为根的高度已经大于已经计算过的根节点的高度,则不用继续访问
if(ans.size() > 0 and height > minHeight) return height;
}
// 如果当前结点pre为根的高度已经大于已经计算过的根节点的高度,则不用继续访问
if(ans.size() > 0 and height > minHeight) return height;
}
// 根据pre邻接的所有方向的高度,返回pre为根节点的最大高度(排除prepre->pre方向,其中prepre为dfs的上一层递归函数的pre)
return height;
}
vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
// 构造邻接表,v[i][j].first表示结点i的第j个子结点,v[i][j].second表示结点i到结点v[i][j]方向的深(高)度。
vector<pair<int,int>> v[n];
for(auto x:edges){
v[x[0]].push_back({x[1],INT_MAX});
v[x[1]].push_back({x[0],INT_MAX});
}
bool visit[n];
for(int i = 0;i < n; ++i){
memset(visit,false,sizeof(visit));
int x = dfs(n,v,i,visit);
// 如果以结点i为根的高度等于最小高度,则将i也加入答案;如果以结点i为根的高度小于最小高度,则清空答案,将i加入答案,最小高度置为结点i为根的高度。
if(x == minHeight){
ans.push_back(i);
}else if(x < minHeight) {
ans.clear();
ans.push_back(i);
minHeight = x;
}
}
return ans;
}
};