[数据结构与算法]数据结构与算法学习笔记（五）树

本文针对树结构中，常见的二叉树和多叉树类型进行介绍和代码分析（主要针对二叉树）。

一、树

1.1 介绍：

????????树结构是一种非线性存储结构，存储的是具有“一对多”关系的数据元素的集合。树结构，可以看作一颗根朝上、叶朝下的倒挂的树，即是由n（n>=1）个有限结点组成一个具有层次关系的集合。每个结点有零个或多个子结点；至少一个根结点（没有父结点的结点）；每一个非根结点有且只有一个父结点；除了根结点外，每个子结点可以分为多个不相交的子树，即树是由根结点和若干棵子树构成的。

1.2 常用的概念：

1）节点深度：对任意节点的深度表示为根节点到该节点的路径长度。所以，根节点深度为0，第二层节点深度为1，以此类推；

2）树的深度：一棵树中，节点的最大深度就是树的深度，也称为高度；

3）节点高度：对于任意节点，叶子节点到该节点的路径长度就是节点x的高度；? ?

4）父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；

5）子节点：一个节点含有的子树的根节点称为该节点的子节点；?兄弟节点：拥有共同父节点的子节点互称为兄弟节点；

6）度：对于一个结点，拥有的子树数称为结点的度（Degree）。一棵树的度，是树内各结点的度的最大值。

7）节点的层次：从根节点开始，根节点为第一层，根的子节点为第二层，以此类推；

8）祖先：任意节点，从根节点到该节点的所有节点都是该节点的祖先，包括该节点自己；

9）后代：对任意节点，从该节点到叶子节点的所有节点都是的后代，包括该节点自己；

10）森林：“互不相交”的树构成的集合就是森林；

1.3 树的种类：

1）有序树和无序树：有序树（结点的子树从左到右看，谁在左边，谁在右边，是有规定的，即称为有序树；有序树中，一个结点最左边的子树称为“第一个孩子”，最右边的称为“最后一个孩子”）和无序树；

2）二叉树（有序树）：树的任意节点至多包含两棵树；具有次序性；

????????二叉树的遍历：从二叉树的根节点出发，按照某种次序访问二叉树中的所有结点，使得每个结点被访问一次，且仅被访问一次；

????????二叉树的访问次序：前序遍历、中序遍历、后序遍历、层次遍历；

????????二叉树的定义（递归定义）：和树的定义类似，但是有一个特点：由一个根节点和两个互不相交的，分别称为根节点的左子树和右子树组成；

????????二叉树的特点：1）每个结点最多有两颗子树；2）左子树与右子树有顺序，即使一颗树中只有一个子树，也需要去判断是左子树还是右子树；

3）斜树：所有结点都只有左子树或只有右子树的二叉树称为斜树（斜树就是单链表）；

4）满二叉树：叶子节点都在同一层并且除叶子节点外的所有节点都有两个子节点；

5）完全二叉树：深度为d（d>1）的二叉树，除第d层外的所有节点构成满二叉树，且第d层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树；

6）严格二叉树：二叉树的每个非终端节点均有非空的左右子树；

7）堆树：是一颗完全二叉树，堆树中某个节点的值总是不大于或不小于其孩子节点的值；堆树中每个节点的子树都是堆树；当父节点的键值总是大于或等于任何一个子节点的键值时为大顶堆； 当父节点的键值总是小于或等于任何一个子节点的键值时为小顶堆。

????????应用：用最大堆、最小堆进行排序。

8）霍夫曼树：带权路径长度（从根结点到该结点之间的路径长度（链接的个数）与该结点的权的乘积）最短的二叉树，称为霍夫曼树（又称为哈夫曼树或最优二叉树）；

????????主要用于数据压缩和编码长度的优化。

9）二叉搜索树（二叉搜索树、二叉排序树、BST）：若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；任意节点的左、右子树也分别为二叉搜索树；没有键值相等的节点；在一般情况下，二叉搜索树的查询效率比链表结构要高。

????????但可能存在二叉搜索树，退化为链表的情况，这时查找的时间复杂度从O(log2 N)退化到了O(N)。如下图：

10）线索二叉树threaded binary tree：在一个二叉树中，实际使用的左右两节点的指针只有n-1个链接，另外n+1个指针都是空链接；线索二叉树，就是要利用这n+1个空链接来存放结点的前驱和后继结点的信息，即这些链接就是“线索”；这样最明显的好处就是，在进行中序遍历时，不需要进行递归与堆栈，直接利用各个结点指针，即可找到其的中序先行者和中序继承者。

????????最大的不同是，线索二叉树中每个结点需要另外加入两个整型数据位LBIT、RBIT（正常指针用1填充、线索用0填充），用来识别左右子树指针是 正常的链接指针 还是 线索（线索用虚线、正常的链接用实线）。

????????缺点：插入和删除结点比较慢。

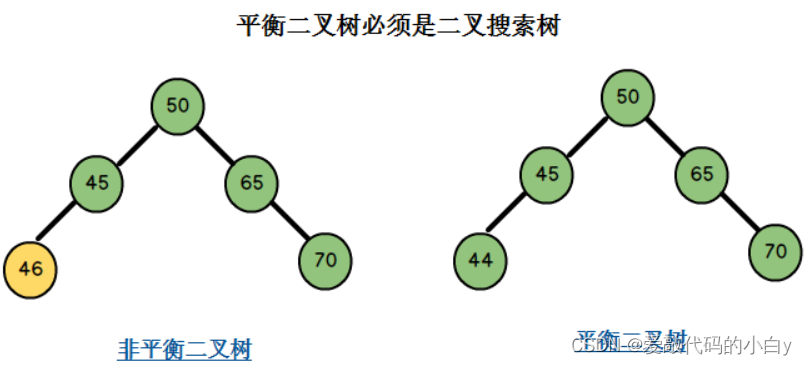
11）平衡二叉树（AVL树）：本质上是一棵空树或各个节点的平衡因子BF（二叉树上节点的左子树与右子树高度差，称为该节点的平衡因子BF(Balance Factor））的绝对值不超过1的二叉搜索树，并且左右两个子树都是一棵平衡二叉树。

????????平衡二叉树很好的解决了由于二叉搜索树高度的越来越高而退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(LogN)，但增加和删除可能需要通过一次或多次树旋转，以降低树的高度，使其达到平衡（这会牺牲掉O(LogN)左右的时间，不过相对于二叉查找树来说，时间上是稳定了许多）。

????????使用场景：用于插入和删除次数比较少但查找多的情况（在windows进程地址空间管理中使用）。

12）红黑树：本质上是每个节点都带有颜色属性（红色或黑色）的二叉搜索树；根节点都是黑色；每个红色节点的两个子节点都是黑色；叶子结点都是黑色的空节点（Nil或Null），即叶子节点不存储数据；从每个叶子到根的所有路径上不能有两个连续的红色节点；从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点；

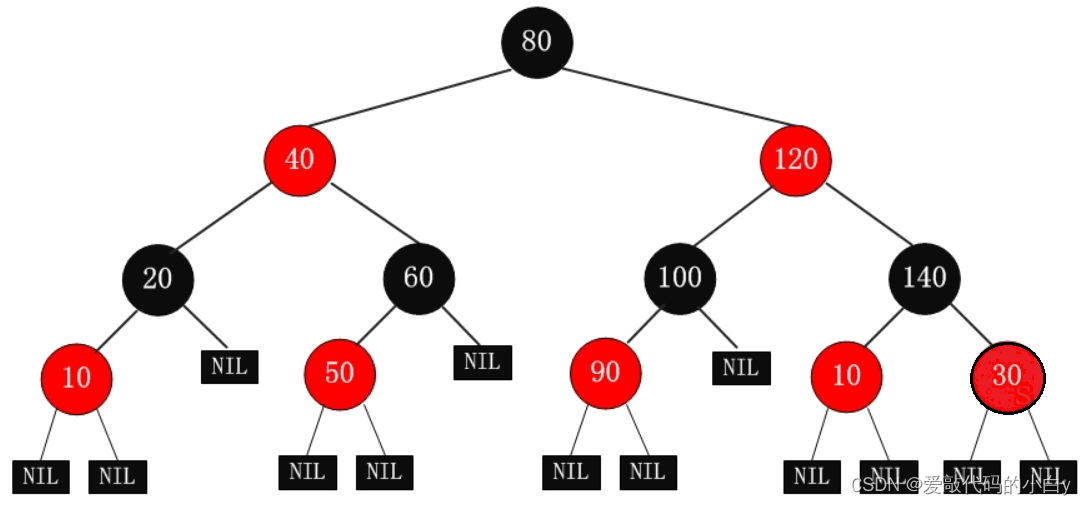
????????红黑树和AVL树的区别：

• 插入：会引起树的不平衡，AVL树和红黑树，最多进行两次旋转操作，二者的时间复杂度O(1)；
• 删除：AVL需要往上回溯多个节点才能实现平衡，平衡的时间复杂度O(log n)，而红黑树最多只需要三次旋转，故时间复杂度O(1)；
• 搜索：AVL的性能高于红黑树；
• 结论：如果有大量的插入、删除操作，则红黑树的效率更高；如果插入删除操作较少，搜索较多，则使用AVL树。红黑树牺牲严格的平衡，换取插入/删除时少量的旋转操作，整体性能优于AVL树。

????????使用场景：（红黑树多用于插入和删除操作）

• c++的STL中，map、set、multimap、multiset等，都是用红黑树实现的；
• 著名的linux进程调度completely fair scheduler（CFS），就是用红黑树管理进程控制块PCB的，进程的虚拟内存空间都存储在一颗红黑树上，每个虚拟内存空间都对应红黑树的一个结点，左指针指向相邻的虚拟内存空间，右指针指向相邻的高地址虚拟内存空间;
• 多路复用技术的Epoll，其核心结构是红黑树 + 双向链表，以支持快速的增删改查。

13）Tri树（字典树）：是一种专门处理字符串匹配的数据结构，用来解决在一组字符串集合中快速查找某个字符串的问题。本质，就是利用字符串之间的公共前缀，将重复的前缀合并在一起。

14）B树（又称B-树）：一棵m阶B树是一棵自平衡的m路搜索树（当m=2时，即常见的二叉搜索树），能够保证数据有序，且<key, value>可存在多叉树的内节点中。与自平衡二叉查找树不同，B-树算法，通过减少定位记录时所经历的中间过程从而加快存取速度，为系统最优化了大块数据的读和写操作，因此普遍运用在数据库和文件系统。

? ? ? ? B-树的特性：

• 所有的叶子结点都出现在同一层上，即根结点到每个叶子结点的长度都相同；
• 除根结点（至少含一个关键字）以外，每个结点：m/2 - 1 <= 关键字个数?<= m - 1 个关键字；
• 一个包含 m 个关键字的结点有 m + 1个孩子（ 两棵子树夹着一个关键字 ）；
• 一个结点中的所有关键字升序排列，即两个关键字 m1 和 m2 之间的孩子结点的所有关键字 key 在 (m1, m2) 内；
• 所有关键字在整颗树中，只出现一次；
• 除根结点（至少有两个子女）、叶子结点以外，所有结点的度数正好是关键字总数加1；

????????AVL树 和 红黑树，都假设所有的数据放在主存当中。但当数据量达到了亿级别，主存当中根本存储不下，我们只能以块的形式从磁盘读取数据，与主存的访问时间相比，磁盘的 I/O 操作相当耗时，而提出 B-树 的主要目的就是减少磁盘的 I/O 操作。大多数平衡树的操作（查找、插入、删除，最大值、最小值等）需要O(h)次磁盘访问操作，其中h=log2 N是树的高度。但是对于B-树而言，树的高度将不再是log2 N (其中N是树中的结点个数），而是一个我们可控的高度h（通过调整 B-树中结点所包含的键（也可称为数据库中的索引，本质上就是在磁盘上的一个位置信息）的数目），使得 B-树的高度保持一个较小的值h=log m/2 N?。一般而言，B-树的结点所包含的键的数目和磁盘块大小一样，从数个到数千个不等。由于B-树的高度 h 可控，所以与 AVL树和红黑树相比，B-树的磁盘访问时间将极大地降低。?

15）B+树：是mysql数据库底层的存储结构，B+树是B-树的一种变形树。

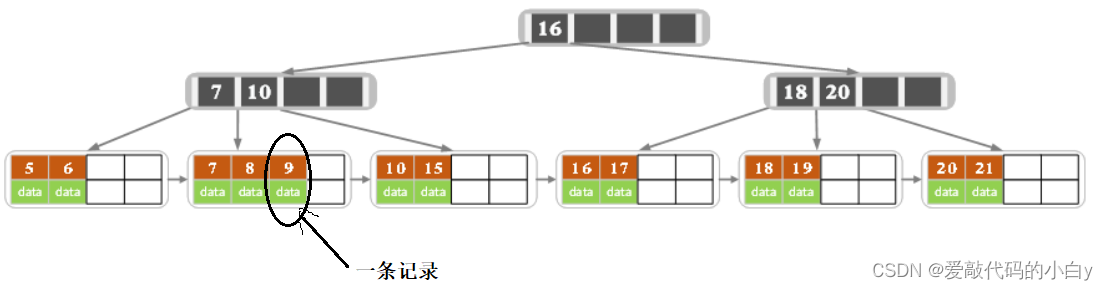????????与B树的差异在于：

• 每个节点中子节点的个数不能超过 m，也不能小于 m/2（例外，根节点的子节点个数可以不超过 m/2）；
• m叉树，内节点只存储索引，只有叶子结点才能存储跟记录有关的信息；
• 通过链表将叶子节点串联在一起，这样可以方便区间范围查找；
• 一般情况，根节点会被存储在内存中，其他节点存储在磁盘中。

????????B+ 树的优点在于：

• 由于B+树在内部节点上，不包含数据信息只包含索引，因此在内存页中能够存放更多的key。 数据存放的更加紧密，具有更好的空间局部性。因此访问叶子节点上关联的数据也具有更好的缓存命中率。
• B+树的叶子结点都是相连的，故对整棵树的遍历只需要一次线性遍历叶子结点即可。而且由于数据顺序排列并且相连，所以便于区间查找和搜索。而B树则需要对每一层进行递归遍历。

????????但是B-树也有优点：由于B-树的每一个节点都包含key和value，因此经常访问的元素可能离根节点更近，因此访问也更迅速。

1.4 常见的存储结构：

? ? ? ? 包括：主存，即随机访问存储器(Random-Access Memory，RAM)、磁盘。这里主要讨论磁盘的存储结构。

? ? ? ? 磁盘的物理结构：磁盘由盘片构成,每个盘片有两面，又称为盘面（Surface），这些盘面覆盖有磁性材料。盘片中央有一个可以旋转的主轴（spindle），他使得盘片以固定的旋转速率旋转，通常是5400转每分钟（Revolution Per Minute,RPM）或者是7200RPM。磁盘包含一个多多个这样的盘片并封装在一个密封的容器内。每个盘片的每个表面，是由一组成为磁道（track）的同心圆组成的，每个磁道被划分为了一组扇区（sector）。每个扇区包含相等数量的数据位，通常是512子节。扇区之间由一些间隔(gap)隔开，不存储数据。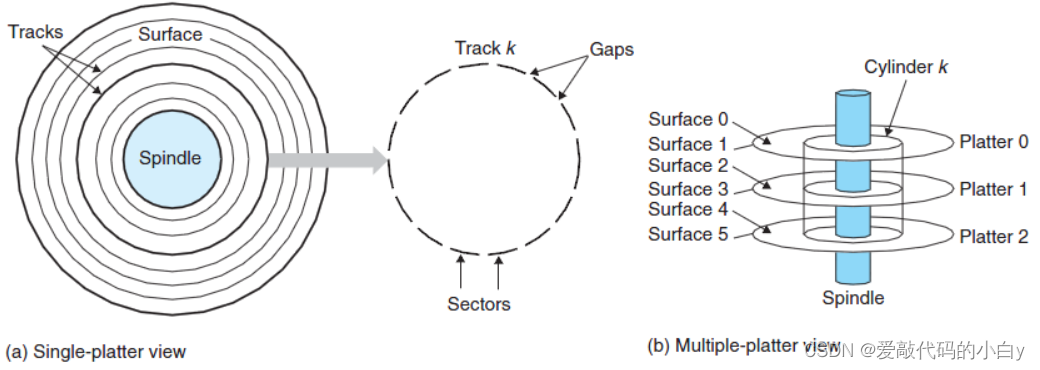

?????????磁盘的读写操作：磁盘用读/写头来读写存储在磁性表面的位，而读写头连接到一个传动臂的一端。通过沿着半径轴前后移动传动臂，驱动器可以将读写头定位到任何磁道上，这称之为寻道操作。一旦定位到磁道后，盘片转动，磁道上的每个位经过磁头时，读写磁头就可以感知到位的值，也可以修改值。对磁盘的访问时间分为：寻道时间、旋转时间、传送时间。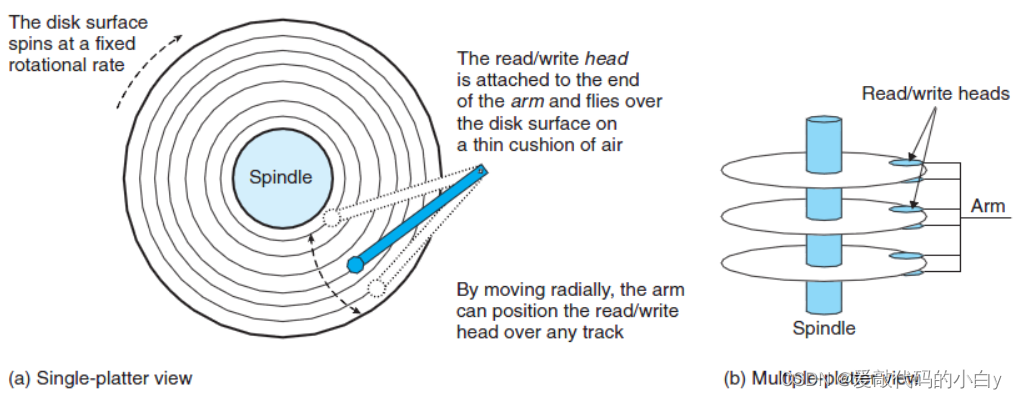

????????由于存储介质的特性，磁盘本身存取就比主存慢很多，再加上机械运动耗费，因此为了提高效率，要尽量减少磁盘I/O，减少读写操作。为了达到这个目的，磁盘往往不是严格按需读取，而是每次都会预读，即使只需要一个字节，磁盘也会从这个位置开始，顺序向后读取一定长度的数据放入内存。这样做的理论依据是计算机科学中著名的局部性原理：当一个数据被用到时，其附近的数据也通常会马上被使用，即程序运行期间所需要的数据通常比较集中。

????????预读的长度一般为页（page）的整倍数。页是计算机管理存储器的逻辑块，硬件及操作系统往往将主存和磁盘存储区分割为连续的大小相等的块，每个存储块称为一页（在许多操作系统中，页得大小通常为4k），主存和磁盘以页为单位交换数据。当程序要读取的数据不在主存中时，会触发一个缺页异常，此时系统会向磁盘发出读盘信号，磁盘会找到数据的起始位置并向后连续读取一页或几页载入内存中，然后异常返回，程序继续运行。

????????文件系统及数据库系统的设计者利用了磁盘预读原理，将一个节点的大小设为等于一个页，这样每个节点只需要一次I/O就可以完全载入。

二、二叉树

2.1 二叉树的性质：

1）在二叉树的第n层最多有2^(n-1)个结点；

2）深度为k的二叉树最多有2^k-1个结点；

3）高度为k的二叉树，总节点数最少为k（左/右斜树刚好是k）；

4）二叉树中，终端结点数（叶子结点数）为n0，度为2的结点数为n2，则n0 = n2 + 1；

证明3）：3.1）对于一个二叉树来说，除了度为 0 的叶子结点（设为 n0）、度为 1 的结点（设为 n1）和度为 2 的结点（设为 n2），那么总结点数：?n = n0 + n1 + n2；3.2）同时，假设树中分枝数为 B，那么总结点数 n = B + 1。而分枝数是可以通过 n1?和 n2?表示的，即 B = n1 + 2 *?n2。所以，得到 n = n1 + 2 * n2 + 1；3.3）通过两种方式得到，n0 = n2 + 1；

注：对于满二叉树而言，第 n 层的结点结点数为2^(n-1)个；深度为 k 的满二叉树必有2^k-1个结点，叶子节点数为2^(k-1)个（故相当于具有 n 个节点的满二叉树的深度为log2(n+1)。

2.2 二叉树的遍历（访问树中所有节点各一次）：

? ? ? ? 遍历的方式：1）通过递归调用（或者借用堆栈完成），来完成中序遍历inorder traversal（左子树-树根-右子树）、前序遍历preorder traversal（树根-左子树-右子树）、后序遍历postorder traversal（左子树-右子树-树根）；2）层序遍历（借用队列完成）；

举例分析：

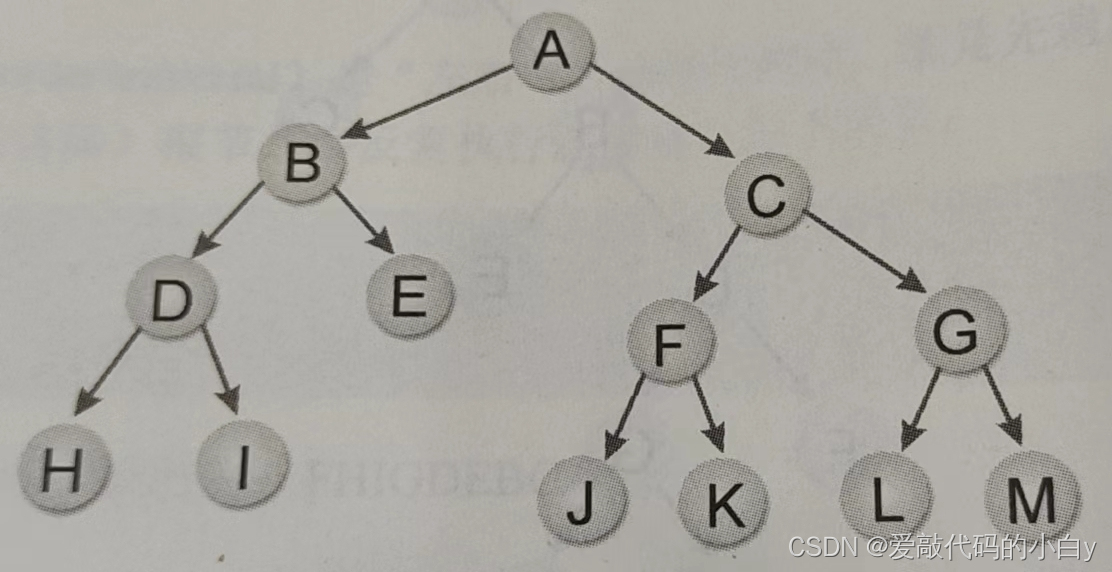
前序遍历：先访问根节点，然后前序遍历左子树，再前序遍历右子树，如A BDHIE CFJKGLM；

中序遍历：先中序遍历左子树，然后访问根节点，再中序遍历右子树，如HDIBE A JFKCLGM ；

后序遍历：先后序遍历左子树，然后后序遍历右子树，再访问根节点，如HIDEB JKFLMGC A；

层序遍历：从树的第一层根节点开始，从上而下逐层遍历，同一层中，按从左到右的顺序遍历，如ABCDEFGHIJKLM；

代码示例：

1）采用递归的写法实现，前序、中序和后序遍历；层序遍历借助的是队列实现；

// 中序遍历
void InorderTraversal(Node* ptr)
{
    if(ptr != NULL)
    {
        InorderTraversal(ptr->left);
        cout << ptr->data << endl;
        InorderTraversal(ptr->right);
    }
}

// 前序遍历
void PreorderTraversal(Node* ptr)
{
    if(ptr != NULL)
    {
        cout << ptr->data << endl;
        PreorderTraversal(ptr->left);
        PreorderTraversal(ptr->right);
    }
}

// 后序遍历
void PostorderTraversal(Node* ptr)
{
    if(ptr != NULL)
    {
        PostorderTraversal(ptr->left);
        PostorderTraversal(ptr->right);
        cout << ptr->data << endl;
    }
}

// 层序遍历
#include<queue>
void LevelorderTraversal(Node* ptr)
{
	queue<Node*> output_queue;
    
    /*写法一：*/
	output_queue.push(ptr);
	output_queue.push(ptr->left);
	output_queue.push(ptr->right);

	cout << (output_queue.front())->data << " ";
	output_queue.pop();

	while (!output_queue.empty())
	{
		if ((output_queue.front())->left != NULL)
		{
			output_queue.push((output_queue.front())->left);
		}
		if ((output_queue.front())->right != NULL)
		{
			output_queue.push((output_queue.front())->right);
		}		
		cout << (output_queue.front())->data << " ";
		output_queue.pop();
	}
    
    ///*写法二：*/
	//BinaryTreeNode<T>* current_node = this->root;
	//output_queue.push(current_node);
	//while (!output_queue.empty()) 
	//{
	//	current_node = output_queue.front(); output_queue.pop();
	//	cout << current_node->data << " ";

	//	if (current_node->left != NULL)
	//	{
	//		output_queue.push(current_node->left);
	//	}

	//	if (current_node->right != NULL)
	//	{
	//		output_queue.push(current_node->right);
	//	}
	//}
}

2） 采用迭代的形式，即借助栈来实现，前序、中序和后序遍历（均可以通过模仿后序遍历引入nullptr和逆序的方法，来实现迭代遍历二叉树）；

// 子树前序、中序和后序遍历(非递归)   
template<class T>
void PreOrderNonRecursiveTraversal()            
{
	// (栈初始化)声明前序遍历栈, 子树根节点指针入栈
	stack<Node<T>*> stack;
	stack.push(this->root);

	while (!stack.empty()) 
	{
		Node<T>* current_node = stack.top(); stack.pop();
		cout << current_node->data << " ";

		// current_node_ptr节点指针的孩子节点进行入栈，先右子节点后左子节点
		if (current_node->right != NULL)
		{
			stack.push(current_node->right);
		}
		if (current_node->left != NULL)
		{
			stack.push(current_node->left);
		}
	}
}

template<class T>
void InOrderNonRecursiveTraversal()       
{
	stack<Node<T>*> stack;
	Node<T>* current_node = this->root;

	while (current_node != NULL || !stack.empty())
	{
		// 先不断将当前节点current_node的左子节点的一直入栈，直到不存在左子节点
		while (current_node != NULL)
		{
			stack.push(current_node);
			current_node = current_node->left;
		}

		// 从栈中，弹出并打印栈顶的节点；并找到该节点的右子节点，用于下次的while循环
		if (!stack.empty()) 
		{
			current_node = stack.top(); stack.pop();
			cout << current_node->data << " ";

			current_node = current_node->right;
		}
	}
} 

template <class T>
void BinaryTree<T>::PostOrderNonRecursiveTraversal()
{
	stack<BinaryTreeNode<T>*> stack;
	stack.push(this->root);

	BinaryTreeNode<T>* current_node = nullptr;
	while (!stack.empty())
	{
		current_node = stack.top(); stack.pop();
		if (current_node != nullptr)
		{
			stack.push(current_node);
			stack.push(nullptr);

			if (current_node->right != nullptr)
			{
				stack.push(current_node->right);
			}
			if (current_node->left != nullptr)
			{
				stack.push(current_node->left);
			}
		}
		else // 只有栈顶current_node为nullptr的时候，才能触发打印操作
		{
			current_node = stack.top(); stack.pop();
			cout << current_node->data << " ";
		}
	}
}

2.3 根据遍历结果，重构二叉树：

1）已知前序和后序遍历结果，不能唯一确定二叉树；

2）已知前序和中序遍历结果，可以确定唯一二叉树；

? ? ? ? 已知前序和中序，重构二叉树的代码分析：先确定每次迭代中子树的根节点（传入的形参中前序数组中第一个元素）；通过根节点将中序数组分割成左子树和右子树两部分，并分别传入函数形参中看作构建新的二叉树，继续递归；

3）已知后序和中序遍历结果，可以确定唯一二叉树；

????????已知中序和后序，重构二叉树的代码分析：先确定每次迭代中子树的根节点（传入的形参中后序数组中的最后一个元素）；通过根节点将中序数组分割成左子树和右子树两部分，并分别传入函数形参中看作构建新的二叉树，继续递归；

????????比如，前序结果：A BDHIE CFJKGLM，中序结果：HDIBE A JFKCLGM，后序结果：HIDEB JKFLMGC A，则中序中A是根节点，HDIBE是A的左子树，JFKCLGM是A的右子树；?对左子树HDIBE进行重新分析，B是根节点，HDI是B的左子树（D是根节点，H是D的左子树，I是D的右子树），E是B的右子树； 对右子树JFKCLGM进行重新分析，C是根节点，JFK是C的左子树（F是根节点，J是F的左子树，K是F的右子树），LGM是C的右子树（G是根节点，L是G的左子树，M是G的右子树）；

#include<iostream>
using namespace std;

template<typename T>
struct Node
{
	Node(int val) : data(val), left(NULL), right(NULL) {}

	T data;
	Node* left;
	Node* right;
};

// 根据前序和中序创建树：二级指针的使用
// 传入的形参包括，树的根节点的二级指针，前序数组，中序数组以及数组中元素个数
template<typename T>
void PreAndInOrderToBT(Node<T>** root, int* preOrder, int* inOrder, int size)
{
	if (size == 0) { return; }     // 递归结束的条件

	(*root) = new Node<T>(preOrder[0]);

	// 找到根节点元素在中序中的位置i
	int i = 0;
	while (inOrder[i] != preOrder[0])
	{
		i++;
	}
	PreAndInOrderToBT(&((*root)->left), &preOrder[1], inOrder, i);                           // 左子树递归求解
	PreAndInOrderToBT(&((*root)->right), &preOrder[i + 1], &inOrder[i + 1], size - i - 1);   // 右子树递归求解
}

// 根据中序，后序创建树
// 传入的形参包括，树的根节点的二级指针，中序数组，后序数组以及数组中元素个数
template<typename T>
void InAndPostOrderToBT(Node<T>** root, int* inOrder, int* postOrder, int size)
{
	if (size == 0) { return; }     // 递归结束的条件

	(*root) = new Node<T>(postOrder[size - 1]);

	// 找到根节点元素在中序中的位置i
	int i = 0;
	while (inOrder[i] != postOrder[size - 1])
	{
		i++;
	}
	InAndPostOrderToBT(&((*root)->left), inOrder, postOrder, i);                           // 左子树递归求解
	InAndPostOrderToBT(&((*root)->right), &inOrder[i + 1], &postOrder[i], size - i - 1);   // 右子树递归求解
}

// 根据前序和中序 或者 中序和后序，创建树
template<typename T>
void CreateTree(Node<T>** root, T* arr1, T* arr2, int size, bool PreAndInOrder = true)
{
	if (PreAndInOrder) { PreAndInOrderToBT(root, arr1, arr2, size); }
	else { InAndPostOrderToBT(root, arr1, arr2, size); }
}

// 子树的递归打印 
template<typename T>
void Print(Node<T>* sub_tree_root, ostream& out)
{
	if (sub_tree_root != NULL)
	{
		out << '('; out << sub_tree_root->data; out << ',';

		if (sub_tree_root->left != NULL)
		{
			Print(sub_tree_root->left, out);
		}
		if (sub_tree_root->right != NULL)
		{
			Print(sub_tree_root->right, out);
		}
		out << ')';
	}
}
template<typename T>
ostream& operator<<(ostream& out, Node<T>* rootNode)
{
	Print(rootNode, out);
	return out;
}

int main()
{
	// 根据前序、中序遍历的结果，来创建二叉树
	int preOrderArr[] = { 0, 1, 3, 6, 5, 9, 2, 4, 8, 7 };  // 前序遍历结果
	int inOrderArr[] = { 6, 3, 1, 9, 5, 0, 8, 4, 2, 7 };   // 中序遍历结果
	int postOrderArr[] = { 6, 3, 9, 5, 1, 8, 4, 7, 2, 0 };

	Node<int>* rootNode = NULL;
	CreateTree(&rootNode, preOrderArr, inOrderArr, 10);        // 通过前序和中序，重构二叉树
	cout << rootNode << endl;

	rootNode = NULL;
	CreateTree(&rootNode, inOrderArr, postOrderArr, 10, false);  // 通过中序和后序，重构二叉树
	cout << rootNode << endl;
}

? ? ? ? 通过中序得到严格二叉树（即非终端节点都有两个子节点），且终端节点是从左到右紧密排列的；通过输出的树的结构字符串，得到树的结构；

#include<iostream>
using namespace std;

template<typename T>
struct Node
{
	Node(int val) :data(val), left(NULL), right(NULL) {}

	T data;
	Node* left;
	Node* right;
};

// create将二叉树的数组表示法（中序表达式）转换成 链表表示法
template<typename T>
Node<T>* LevelOrderToBT(T* LevelOrderArr, int index, int ArraySize)
{
	if (index == 0 || index >= ArraySize) { return NULL; }   // 作为出口条件
	else
	{
		Node<T>* tempNode = new Node<T>(LevelOrderArr[index]);
		tempNode->left = NULL;
		tempNode->right = NULL;

		tempNode->left = LevelOrderToBT(LevelOrderArr, 2 * index, ArraySize);     	// 建立左子树
		tempNode->right = LevelOrderToBT(LevelOrderArr, 2 * index + 1, ArraySize);	// 建立右子树
		return tempNode;
	}
}

// 子树的递归打印 
template<class T>
void Print(Node<T>* sub_tree_root, ostream& out)
{
	if (sub_tree_root != NULL)
	{
		out << '('; out << sub_tree_root->data; out << ',';

		if (sub_tree_root->left != NULL)
		{
			Print(sub_tree_root->left, out);
		}
		if (sub_tree_root->right != NULL)
		{
			Print(sub_tree_root->right, out);
		}
		out << ')';
	}
}
template<class T>
ostream& operator<<(ostream& out, Node<T>* rootNode)
{
	Print(rootNode, out);
	return out;
}

int main()
{
	// 根据层序遍历的结果，来创建二叉树：
	// 数组中的第一个0，不插入二叉树中，只是为了便于建立层序和数组下标的关系
	int levelOrderArr[] = { 0, 0, 1, 2, 3, 5, 4, 7, 6, 9, 8 };
	Node<int>* rootNode =LevelOrderToBT(levelOrderArr, 1, 11);
	cout << rootNode << endl;

	return 0;
}

2.4 二叉搜索树节点的查找、插入和删除：?

????????二叉搜索树的查找算法：找到BST中，与val值相同的节点的指针；

// 查找二叉树某键值的函数
Node* search(Node* ptr, int val)
{
    while(true)
    {
        if(ptr == NULL) { return NULL; }    
        if(ptr->data > val) { ptr = ptr->left; }
        if(ptr->data < val) { ptr = ptr->right; }
        if(ptr->data == val) { return ptr; }
    }
}

? ? ? ? 二叉搜索树的插入算法：和查找算法相似，重点是插入后仍要保持二叉搜索树的性质；只需要保证查找算法中无法找到该节点，然后再添加元素；如果出现查找到该元素已经存在在BST中的某个节点中，则立即跳出while循环，表示添加成功（因已经存在在BST中，为了满足BST中不能有相同的键值的节点的存在）；?

// 将指定的值加入到二叉搜索树
void add(Node** rootNode, int data)
{
	//int flag = 0;            // 用来纪录是否插入新的节点

	// 建立节点内容
	Node* newnode = (Node*)malloc(sizeof(Node));
	newnode->data = data;
	newnode->left = NULL;
	newnode->right = NULL;

	if (*rootNode == NULL)    // 如果为空的二叉搜索树，便将新的节点设定为根节点
	{ 
		*rootNode = newnode;
	}
	else
	{
		Node* currentNode = *rootNode;   // 指定一个指针指向根节点
		while (true)
		{
			if (data < currentNode->data)
			{ 
				// 当前节点的左节点存放比其数据小的节点
				if (currentNode->left == NULL)
				{
					currentNode->left = newnode;
					break;
				}
				else
				{
					// 当当前节点的左节点存放有数据时，要将左节点的重新作为当前节点并继续while循环
					currentNode = currentNode->left;
				}	
			}
			if (data > currentNode->data)
			{ 
				// 当前节点的右节点存放比其数据大的节点
				if (currentNode->right == NULL)
				{
					currentNode->right = newnode;
					break;
				}
				else
				{
					// 当当前节点的右节点存放有数据时，要将右节点的重新作为当前节点并继续while循环
					currentNode = currentNode->right;
				}
			}
			// 二叉搜索树，不能有相同键值的节点存在
			if (data == currentNode->data)
			{
				cout << data << " have been existed" << endl;
				break;
			}
		}	
	}
}

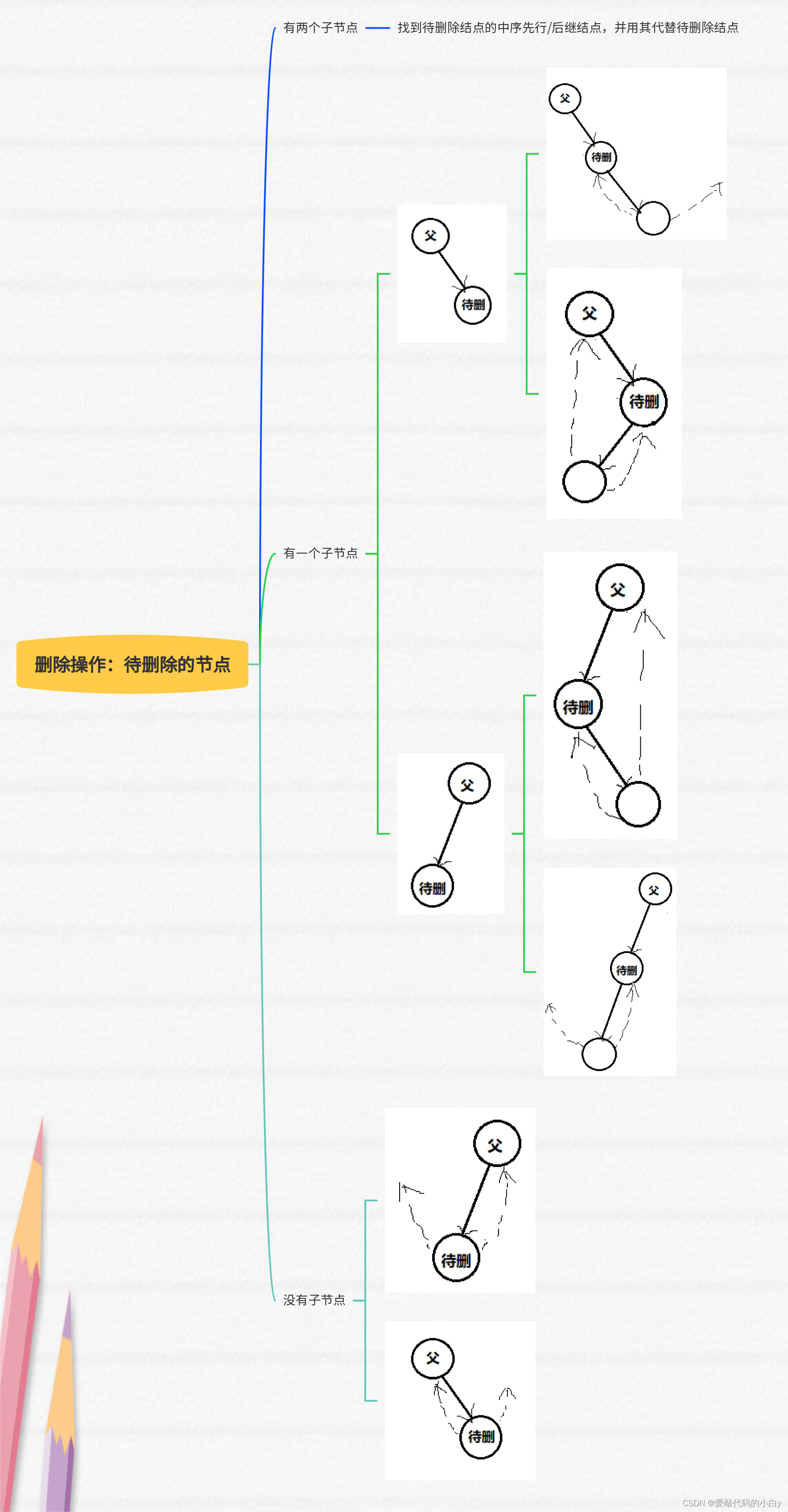
? ? ? ? 二叉搜索树的删除算法：1）删除的节点为叶子节点，只要将其连接的父节点指向NULL即可；2）删除的节点只有一棵子树，就将其右指针放在其父节点的左指针；3）删除的节点有两棵子树，有两种删除的方式：①找到中序立即先行者（inorder immediate predecessor），即是将欲删除节点的左子树中最大者（即是中序立即先行者）向上提；②?找到中序立即后继者( inorder? immediate?successor），即是将欲删除节点的右子树中最小者（即是中序立即后继者）向上提；

Node* Delete(Node* ptr, int val, int choice)  // choice==1（用中序先行者代替待删除的节点）或2（用中序后继者代替待删除的节点）
{
	if (ptr == NULL) { return ptr; }
	else
	{
		Node* tempNode1 = ptr;
		Node* pretempNode1 = ptr;
		while (true)
		{
			if (tempNode1->data > val) { pretempNode1 = tempNode1; tempNode1 = tempNode1->left; }
			if (tempNode1->data < val) { pretempNode1 = tempNode1; tempNode1 = tempNode1->right; }		
			// 找到了元素对应的BST中，节点的具体位置，即tempNode1指向的是待删除的节点
			if (tempNode1->data == val)
			{
				// 1、如果要删除的节点是BST中的叶子节点
				if (tempNode1->left == NULL && tempNode1->right == NULL)
				{
					if (pretempNode1->left->data == val)  // 要删除的节点是tempNode1的左叶子节点
					{
						delete pretempNode1->left;
						pretempNode1->left = nullptr;
						return ptr;
					}
					if (pretempNode1->right->data == val) // 要删除的节点是tempNode1的右叶子节点
					{
						delete pretempNode1->right;
						pretempNode1->right = nullptr;
						return ptr;
					}
				}

				// 2、如果要删除的节点只有一棵子树
				if (tempNode1->left == NULL && tempNode1->right != NULL)
				{
					tempNode1->data = tempNode1->right->data;
					delete tempNode1->right;
					tempNode1->right = nullptr;
					return ptr;
				}
				if (tempNode1->left != NULL && tempNode1->right == NULL)
				{
					tempNode1->data = tempNode1->left->data;
					delete tempNode1->left;
					tempNode1->left = nullptr;
					return ptr;
				}

				// 3、如果要删除的节点的有两棵子树时，有两种符合二叉搜索树的删除方式：   
				Node* tempNode2 = NULL;
				Node* pretempNode2 = NULL;
				if (tempNode1->left != NULL && tempNode1->right != NULL)
				{
					// 做法一：用中序立即先行者替换被删除的节点
					if (choice == 1)
					{
						pretempNode2 = tempNode1;
						tempNode2 = tempNode1->left;			
						while (tempNode2->right != NULL)
						{
							pretempNode2 = tempNode2;
							tempNode2 = tempNode2->right;
						}
						// 此时，tempNode2指向的是中序立即先行者/中序立即后继者
						tempNode1->data = tempNode2->data;
						delete pretempNode2->left;
						pretempNode2->left = nullptr;
						return ptr;
					}

					// 做法二：用中序立即后继者替换被删除的节点
					if (choice == 2)
					{
						pretempNode2 = tempNode1;
						tempNode2 = tempNode1->right;
						while (tempNode2->left != NULL)
						{
							pretempNode2 = tempNode2;
							tempNode2 = tempNode2->left;
						}
						// 此时，tempNode2指向的是中序立即先行者/中序立即后继者
						tempNode1->data = tempNode2->data;
						delete pretempNode2->right;
						pretempNode2->right = nullptr;
						return ptr;
					}				
				}
			}
		}
	}
}

三、构建左右高度差不超过1的二叉树（非平衡二叉树）?

代码分析：按照先左后右的原则构建非平衡二叉树（左右子树的高度差不超过1），包括了计算树的高度、节点个数、判断树是否为空、查找、插入、遍历（前序、中序和后序遍历（递归/非递归））；以及通过前序、中序遍历的结果来创建平衡二叉树（通过前序和中序或者中序和后序，则可以唯一确定一棵二叉树）；通过前序的遍历的结果来创建平衡二叉树（树不唯一）；通过重载==运算符，判断两个二叉树是否相等；通过调用copy()函数，进行树的拷贝构造；通过重载<<运算符，来实现树的结构打印；

举例：用0~7构建左右高度差小于1的二叉树?，顺序是先左后右且左右子树的高度差不超过1；树的生长过程（先有左子树再有右子树）：(0)、(0(1))、(0(1)(2))、(0(1(3))(2))、(0(1(3))(2(4)))、(0(1(3)(5))(2(4)))、(0(1(3(6))(5))(2(4)))、(0(1(3(6))(5))(2(4)(7)))?

BinaryTree.hpp?

#pragma once
#include <iostream>
#include <stack>
#include <queue>
using namespace std;

// 二叉树结点模板结构体
template <class T>
struct BinaryTreeNode 
{
	// 无参构造函数
	BinaryTreeNode() : left(NULL), right(NULL) {}                                         
	// 构造函数：数据项和左右孩子
	BinaryTreeNode(T data, BinaryTreeNode<T>* left = NULL, BinaryTreeNode<T>* right = NULL) : data(data), left(left), right(right) {}

	T data;                    // 二叉树结点数据项
	BinaryTreeNode<T>* left;   // 左子结点指针
	BinaryTreeNode<T>* right;  // 右子结点指针
};

// 二叉树模板类
template <class T>
class BinaryTree 
{
public:
	BinaryTree() : root(NULL) {}                                                                    // 构造函数(无参数)	
	BinaryTree(T data) { this->insert(this->root, data); }                                          // 构造函数(根节点数据项)	
	BinaryTree(const BinaryTree<T>& bin_tree) { this->root = this->copy(bin_tree.GetRoot()); }              // 拷贝构造函数
	~BinaryTree() { this->clear(this->root); }
	
	bool IsEmpty() { return (this->root == NULL); }                 // 是否为空树 
	BinaryTreeNode<T>* GetRoot() const { return this->root; }     // 获取根节点
	int Height() { return this->height(this->root); }
	int Size() { return this->size(this->root); }

	// 获取节点的父节点
	BinaryTreeNode<T>* Parent(BinaryTreeNode<T>* node) { return parent(this->root, node); }

	bool Insert(T data) { return this->insert(this->root, data); }
	bool Find(T data) { return this->find(this->root, data); }
	
	// 遍历
	// 也可以通过函数指针作为参数：void PreOrderTraversal(void(*visit)(ChildSiblingNode<T>*)) { PreOrderTraversal(this->root, visit); }
	void PreOrderTraversal() { this->PreOrderTraversal(this->root); }          // 前序遍历(递归/非递归)
	void PreOrderNonRecursiveTraversal();
	void InOrderTraversal() { this->InOrderTraversal(this->root); }             // 中序遍历(递归/非递归)
	void InOrderNonRecursiveTraversal();
	void PostOrderTraversal() { this->PostOrderTraversal(this->root); }        // 后序遍历(递归/非递归)
	void PostOrderNonRecursiveTraversal();
	void LevelOrderTraversal();                                                 // 层序遍历

	// 使用前序遍历和中序遍历结果, 创建二叉树：  pre_order_str 前序遍历字符串  in_order_str 中序遍历字符串  str_length 字符串长度
	void CreateBTByPreAndInOrder(T* preOrderArr, T* inOrderArr, int ArraySize)
	{
		this->createBTByPreAndInOrder(preOrderArr, inOrderArr, ArraySize, this->root);
	}

	// create将二叉树的数组表示法（中序表达式）转换成 链表表示法
	void CreateBTByLevelOrder(T* sequence, int index, int ArraySize) { this->root = this->create(sequence, index, ArraySize); }

	// 使用字符串创建子女兄弟树 
	void CreateTreeByStr(char*& str) { this->CreateTreeByStrRecursive(this->root, str); }
protected:
	BinaryTreeNode<T>* root; // 根结点

	// 采用递归的手段，完成二叉树的高度、节点个数、查找、复制、寻找父节点以及清空整个二叉树
	int height(BinaryTreeNode<T>* sub_tree_root) const;
	int size(BinaryTreeNode<T>* sub_tree_root) const;
	void clear(BinaryTreeNode<T>*& sub_tree_root);
	bool find(BinaryTreeNode<T>* sub_tree_root, T value) const;	
	BinaryTreeNode<T>* copy(BinaryTreeNode<T>* src_sub_tree_root);   // 递归的将根节点是src_sub_tree_root的BT树，复制到新的根节点所在的二叉树，并返回新的根节点
	BinaryTreeNode<T>* parent(BinaryTreeNode<T>* sub_tree_root, BinaryTreeNode<T>* node);

	// 采用递归的手段，完成二叉树中节点的插入
	bool insert(BinaryTreeNode<T>*& sub_tree_root, T data);

	// 前、中、后序遍历(递归)
	void PreOrderTraversal(BinaryTreeNode<T>* sub_tree_root);
	void InOrderTraversal(BinaryTreeNode<T>* sub_tree_root);
	void PostOrderTraversal(BinaryTreeNode<T>* sub_tree_root);

	// 打印二叉树，使用'('，','，')' 
	void Print(BinaryTreeNode<T>* sub_tree_root, ostream& out);
	template<class U>
	friend ostream& operator<<(ostream& out, BinaryTree<U>& bin_tree);                        // 输出二叉树

	// 判断两颗二叉树是否相同(递归)
	static bool Equal(BinaryTreeNode<T>* root_ptr_a, BinaryTreeNode<T>* root_ptr_b);
	template<class U>
	friend bool operator==(const BinaryTree<U>& bin_tree_1, const BinaryTree<U>& bin_tree_2); // 判断两颗树相同

	// 使用前序遍历和中序遍历结果, 创建二叉子树(递归)
	void createBTByPreAndInOrder(T* preOrderArr, T* inOrderArr, int ArraySize, BinaryTreeNode<T>*& sub_tree_root);
	// create将二叉树的数组表示法（中序表达式）转换成 链表表示法
	BinaryTreeNode<T>* create(T* inOrderArr, int index, int ArraySize);
	// 使用字符串创建子女兄弟树 
	void CreateTreeByStrRecursive(BinaryTreeNode<T>*& sub_tree_root, char*& str);
};

// 求子树的高度(递归)  sub_tree_root 子树根节点指针  
template<class T>
int BinaryTree<T>::height(BinaryTreeNode<T>* sub_tree_root) const
{
	// 如果子树根节点为空, 则返回0
	if (sub_tree_root == NULL) { return 0; }

	int left_sub_tree_height = height(sub_tree_root->left);    // 递归求左子树高度
	int right_sub_tree_height = height(sub_tree_root->right);  // 递归求右子树高度

	// 树高度 = 最高的左右子树高度 + 1
	return (left_sub_tree_height > right_sub_tree_height) ? (left_sub_tree_height + 1) : (right_sub_tree_height + 1);
}

// 求子树的size(递归)  
template<class T>
int BinaryTree<T>::size(BinaryTreeNode<T>* sub_tree_root) const
{
	if (sub_tree_root == NULL) { return 0; }

	int left_sub_tree_size = size(sub_tree_root->left);    // 递归求左子树size
	int right_sub_tree_size = size(sub_tree_root->right);  // 递归求右子树size

	return (1 + left_sub_tree_size + right_sub_tree_size);
}

// 删除子树
template <class T>
void BinaryTree<T>::clear(BinaryTreeNode<T>*& sub_tree_root) 
{
	if (sub_tree_root == NULL) { return; }

	this->clear(sub_tree_root->left);
	this->clear(sub_tree_root->right);

	delete sub_tree_root;
	sub_tree_root = nullptr;
}

// 查找数据是否在(子)树中(递归) 
template<class T>
bool BinaryTree<T>::find(BinaryTreeNode<T>* sub_tree_root, T value) const 
{
	if (sub_tree_root == NULL) { return false; }

	if (sub_tree_root->data == value) { return true; }

	if (find(sub_tree_root->left, value)) { return true; }   // 一旦找到，立即返回true
	if (find(sub_tree_root->right, value)) { return true; }
}

// 复制二叉树(递归)  src_sub_tree_root源树根节点  new_sub_tree_root新树根节点
template<class T>
BinaryTreeNode<T>* BinaryTree<T>::copy(BinaryTreeNode<T>* src_sub_tree_root) 
{
	if (src_sub_tree_root == NULL) { return NULL; }

	BinaryTreeNode<T>* new_sub_tree_root = new BinaryTreeNode<T>(src_sub_tree_root->data);

	new_sub_tree_root->left = copy(src_sub_tree_root->left);
	new_sub_tree_root->right = copy(src_sub_tree_root->right);

	return new_sub_tree_root;
}

// 子树获取节点的父节点  sub_tree_root子树根节点指针  node节点指针  节点的(位于子树内的)父节点指针
template<class T>
BinaryTreeNode<T>* BinaryTree<T>::parent(BinaryTreeNode<T>* sub_tree_root, BinaryTreeNode<T>* node) 
{
	while (Find(node->data))   // 保证node节点在this->root根节点所在的二叉树中
	{
		// 如果子树根为NULL, 则返回NULL
		if (sub_tree_root == NULL) { return NULL; }

		// 如果子树根节点sub_tree_root的左/右子节点就是node, 则返回子树根结点
		if (sub_tree_root->left == node || sub_tree_root->right == node) { return sub_tree_root; }

		BinaryTreeNode<T>* parent = this->parent(sub_tree_root->left, node);  // 一旦找到，立即返回parent父节点
		if (parent == NULL)
		{
			parent = this->parent(sub_tree_root->right, node);
		}
		return parent;
	}
}

// 子树插入数据 sub_tree_root 子树根结点
template<class T>
bool BinaryTree<T>::insert(BinaryTreeNode<T>*& sub_tree_root, T data)
{
	if (sub_tree_root == NULL)
	{
		sub_tree_root = new BinaryTreeNode<T>(data);
		return true;
	}

	int left_sub_tree_height = height(sub_tree_root->left);
	int right_sub_tree_height = height(sub_tree_root->right);
	// 如果根节点的左子树的高度高于右子树，则将节点插在右子树中；否则插入在左子树中；
	if (left_sub_tree_height > right_sub_tree_height)
	{
		return insert(sub_tree_root->right, data);
	}
	else
	{
		return insert(sub_tree_root->left, data);
	}
}

 // 子树前序、中序和后序遍历(递归)   
template<class T>
void BinaryTree<T>::PreOrderTraversal(BinaryTreeNode<T>* sub_tree_root)
{
	if (sub_tree_root != NULL)
	{
		cout << sub_tree_root->data << " ";
		PreOrderTraversal(sub_tree_root->left);
		PreOrderTraversal(sub_tree_root->right);
	}
}
template<class T>
void BinaryTree<T>::InOrderTraversal(BinaryTreeNode<T>* sub_tree_root)
{
	if (sub_tree_root != NULL)
	{
		InOrderTraversal(sub_tree_root->left);
		cout << sub_tree_root->data << " ";
		InOrderTraversal(sub_tree_root->right);
	}
}
template<class T>
void BinaryTree<T>::PostOrderTraversal(BinaryTreeNode<T>* sub_tree_root)
{
	if (sub_tree_root != NULL)
	{
		PostOrderTraversal(sub_tree_root->left);
		PostOrderTraversal(sub_tree_root->right);
		cout << sub_tree_root->data << " ";
	}
}

// 子树前序、中序和后序遍历(非递归)   
template<class T>
void BinaryTree<T>::PreOrderNonRecursiveTraversal()            
{
	// (栈初始化)声明前序遍历栈, 子树根节点指针入栈
	stack<BinaryTreeNode<T>*> stack;
	stack.push(this->root);

	while (!stack.empty()) 
	{
		BinaryTreeNode<T>* current_node = stack.top(); stack.pop();
		cout << current_node->data << " ";

		// current_node_ptr节点指针的孩子节点进行入栈，先右子节点后左子节点
		if (current_node->right != NULL)
		{
			stack.push(current_node->right);
		}
		if (current_node->left != NULL)
		{
			stack.push(current_node->left);
		}
	}
}
template<class T>
void BinaryTree<T>::InOrderNonRecursiveTraversal()       
{
	stack<BinaryTreeNode<T>*> stack;
	BinaryTreeNode<T>* current_node = this->root;

	while (current_node != NULL || !stack.empty())
	{
		// 先不断将当前节点current_node的左子节点的一直入栈，直到不存在左子节点
		while (current_node != NULL)
		{
			stack.push(current_node);
			current_node = current_node->left;
		}

		// 从栈中，弹出并打印栈顶的节点；并找到该节点的右子节点，用于下次的while循环
		if (!stack.empty()) 
		{
			current_node = stack.top(); stack.pop();
			cout << current_node->data << " ";

			current_node = current_node->right;
		}
	}
} 
// 后序遍历栈结点模板类
template <class T>
class PostOrderStackNode
{
public:
	explicit PostOrderStackNode(BinaryTreeNode<T>* node = NULL)
	{
		this->node = node;
		tag = LEFT;
	}

	BinaryTreeNode<T>* node;       // 二叉树结点指针
	enum TAG                       // 定义标签
	{ 
		LEFT = 0, RIGHT 
	} tag;                
};
template <class T>
void BinaryTree<T>::PostOrderNonRecursiveTraversal()
{
	stack<PostOrderStackNode<T>> stack;
	BinaryTreeNode<T>* current_node = this->root;
	do 
	{
		while (current_node != NULL)
		{
			PostOrderStackNode<T> traverse_node(current_node);
			stack.push(traverse_node);
			current_node = current_node->left;
		}

		bool left_unfinished = true;
		while (left_unfinished && !stack.empty()) 
		{
			PostOrderStackNode<T> current_traverse_node = stack.top(); stack.pop();
			current_node = current_traverse_node.node;
			switch (current_traverse_node.tag)
			{
			case PostOrderStackNode<T>::LEFT:
				current_traverse_node.tag = PostOrderStackNode<T>::RIGHT;
				stack.push(current_traverse_node);
				current_node = current_node->right;

				left_unfinished = false;
				break;
			case PostOrderStackNode<T>::RIGHT:
				cout << current_node->data << " ";
				break;
			}
		}
	} while (!stack.empty());
}

// 子树层序遍历  
template<class T>
void BinaryTree<T>::LevelOrderTraversal()
{
	queue<BinaryTreeNode<T>*> queue;

	BinaryTreeNode<T>* current_node = this->root;
	queue.push(current_node);
	while (!queue.empty()) 
	{
		current_node = queue.front(); queue.pop();
		cout << current_node->data << " ";

		if (current_node->left != NULL)
		{
			queue.push(current_node->left);
		}

		if (current_node->right != NULL)
		{
			queue.push(current_node->right);
		}
	}
}

// 判断两颗二叉树是否相同(递归)
template<class T>
bool BinaryTree<T>::Equal(BinaryTreeNode<T>* root_ptr_a, BinaryTreeNode<T>* root_ptr_b) 
{
	if (root_ptr_a == NULL && root_ptr_b == NULL) { return true; }

	if (root_ptr_a != NULL && root_ptr_b != NULL && root_ptr_a->data == root_ptr_b->data
		&& BinaryTree<T>::Equal(root_ptr_a->left, root_ptr_b->left)
		&& BinaryTree<T>::Equal(root_ptr_a->right, root_ptr_b->right))
	{ return true; }
	else  { return false; }
}
template<class U>
bool operator==(const BinaryTree<U>& bin_tree_1, const BinaryTree<U>& bin_tree_2) 
{
	return (BinaryTree<U>::Equal(bin_tree_1.GetRoot(), bin_tree_2.GetRoot()));
}

// 子树的递归打印 
template<class U>
void BinaryTree<U>::Print(BinaryTreeNode<U>* sub_tree_root, ostream& out)
{
	if (sub_tree_root != NULL)
	{
		out << '('; out << sub_tree_root->data; out << ',';

		if (sub_tree_root->left != NULL)
		{
			this->Print(sub_tree_root->left, out);
		}
		if (sub_tree_root->right != NULL)
		{
			this->Print(sub_tree_root->right, out);
		}	
		
		 等价于：
		//for (BinaryTreeNode<T>* cur = sub_tree_root->left; cur != NULL; cur = cur->right)
		//{
		//	this->Print(cur, out);
		//}

		out << ')';
	}
}
template<class U>
ostream& operator<<(ostream& out, BinaryTree<U>& Tree) 
{
	Tree.Print(Tree.GetRoot(), out);
	return out;
}


// 使用前序遍历和中序遍历结果, 创建二叉子树(递归)  
template<class T>
void BinaryTree<T>::createBTByPreAndInOrder(T* preOrderArr, T* inOrderArr, int ArraySize, BinaryTreeNode<T>*& sub_tree_root)
{
	if (ArraySize == 0) { return; }

	int pivot = 0;
	T cur_root_value = preOrderArr[0];

	while (cur_root_value != inOrderArr[pivot])
	{
		pivot++;
	}

	sub_tree_root = new BinaryTreeNode<T>(cur_root_value);
	createBTByPreAndInOrder(preOrderArr + 1, inOrderArr, pivot, sub_tree_root->left);
	createBTByPreAndInOrder(preOrderArr + pivot + 1, inOrderArr + pivot + 1, ArraySize - pivot - 1, sub_tree_root->right);
} 

// create将二叉树的数组表示法（中序表达式）转换成 链表表示法
template<class T>
BinaryTreeNode<T>* BinaryTree<T>::create(T* inOrderArr, int index, int ArraySize)
{
	if (index == 0 || index >= ArraySize) { return NULL; }   // 作为出口条件
	else
	{
		BinaryTreeNode<T>* tempNode = new BinaryTreeNode<T>(inOrderArr[index]);
		tempNode->left = NULL;
		tempNode->right = NULL;

		tempNode->left = create(inOrderArr, 2 * index, ArraySize);     	// 建立左子树
		tempNode->right = create(inOrderArr, 2 * index + 1, ArraySize);	// 建立右子树
		return tempNode;
	}
}

// 使用字符串创建子女兄弟树 
template <class T>
void BinaryTree<T>::CreateTreeByStrRecursive(BinaryTreeNode<T>*& sub_tree_root, char*& str)
{
	if (*str == '\0') { return; }

	if (*str == ')')
	{
		str++;       // 下一个子节点
		return;
	}

	while (*str == '(') { str++; }

	sub_tree_root = new BinaryTreeNode<T>(*(str++) - '0');   // 将要插入的数据从字符型转换为整型
	CreateTreeByStrRecursive(sub_tree_root->left, str);
	CreateTreeByStrRecursive(sub_tree_root->right, str);
}

main.cpp

#include "BinaryTree.hpp"

int main()
{
	int num = 7;
	BinaryTree<int> binarytree;
	for (int i = 0; i < num; i++)
	{
		binarytree.Insert(i);
	}
	cout << binarytree << endl;     // 调用重载输出流ostream& operator<<(ostream& out, BinaryTree<U>& Tree) 

	BinaryTree<int> binarytree2(binarytree);    // 调用拷贝构造函数
	if (binarytree2 == binarytree)  // 调用重载的等号运算符bool operator==(const BinaryTree<U>& bin_tree_1, const BinaryTree<U>& bin_tree_2) 
	{
		cout << binarytree2 << endl;
	}
	
	cout << "二叉树的深度：" << binarytree.Height() << endl;
	cout << "二叉树的大小：" << binarytree.Size() << endl;

	BinaryTreeNode<int>* rootNode = binarytree.GetRoot();
	cout << "根节点: " << rootNode->data << endl;
	cout << "根节点左孩子：" << (rootNode->left)->data << endl;
	cout << "根节点右孩子：" << (rootNode->right)->data << endl;

	BinaryTreeNode<int>* target_ptr = rootNode->left;
	BinaryTreeNode<int>* target_parent_ptr = binarytree.Parent(target_ptr);
	cout << target_ptr->data << "的父节点： " << target_parent_ptr->data << endl;


	cout << "前序遍历(递归)："; binarytree.PreOrderTraversal(); cout << endl;
	cout << "前序遍历(非递归)："; binarytree.PreOrderNonRecursiveTraversal(); cout << endl;

	cout << "中序遍历(递归)："; binarytree.InOrderTraversal(); cout << endl;
	cout << "中序遍历(非递归)："; binarytree.InOrderNonRecursiveTraversal(); cout << endl;

	cout << "后序遍历(递归)："; binarytree.PostOrderTraversal(); cout << endl;
	cout << "后序遍历(非递归)："; binarytree.PostOrderNonRecursiveTraversal(); cout << endl;

	cout << "层序遍历(非递归)："; binarytree.LevelOrderTraversal(); cout << endl;


	if (binarytree.Find(5)) { cout << "5 is in the tree" << endl; }
	else { cout << "5 isn't in the tree" << endl; }
	if (binarytree.Find(9)) { cout << "9 is in the tree" << endl; }
	else { cout << "9 isn't in the tree" << endl; }


	// 根据前序、中序遍历的结果，来创建二叉树
	BinaryTree<int> binarytree3;
	int pre_order_traverse_arr1[] = { 0, 1, 3, 6, 5, 9, 2, 4, 8, 7 };  // 前序遍历结果
	int in_order_traverse_arr1[] = { 6, 3, 1, 9, 5, 0, 8, 4, 2, 7 };   // 中序遍历结果
	binarytree3.CreateBTByPreAndInOrder(pre_order_traverse_arr1, in_order_traverse_arr1, 10);
	cout << binarytree3 << endl;

	// 根据层序遍历的结果，来创建二叉树：
	// 数组中的第一个0，不插入二叉树中，只是为了便于建立层序和数组下标的关系
	int in_order_traverse_arr[] = { 0, 0, 1, 2, 3, 5, 4, 7, 6, 9, 8 };
	binarytree3.CreateBTByLevelOrder(in_order_traverse_arr, 1, 11);
	cout << binarytree3 << endl;

	// 测试使用字符串创建子女孩子树
	char* str = (char*)"(0(1(3)(4))(2(5)(6)))";
	binarytree3.CreateTreeByStr(str);
	cout << binarytree3 << endl;
    
    return 0;
}

四、构建二叉搜索树

? ? ? ?存储结构的表示方法：1）使用连续内存空间的一维数组（对数组中间的元素进行删除时，需要移动大量的元素）；2）链表（删除和增加有节点时，比较方便）；

4.1 一维数组构建二叉搜索树

树中，各个节点的索引值：1 ~ (2^level - 1)；

下标值的关系：①左子树下标值是父节点下标值 * 2；②右子树下标值是父节点下标值 * 2 + 1；

main.cpp

#include <iostream>
using namespace std;
#define ArraySize 9

struct Node              // 节点链表结构声明
{
	int data;            // 节点数据
	Node* left;          // 节点左指针和右指针
	Node* right;		
};

void CreateTree(int data[], int tree[], int& max_index)
{
	// 一维数组表示法：
	// 树的节点的索引值：1~(2^level-1)，则会出现左节点的下标值是父节点下标值*2；右节点的下标值是父节点下标值*2+1；
	for (int i = 0; i < ArraySize; i++)           // 把原始数组中的值逐一对比
	{
		int index = 1;
		while (tree[index] != 0)           // 比较树根和数组内的值
		{
			if (data[i] > tree[index])    // 如果数组内的值大于树根，则与右子树比较
			{
				index = index * 2 + 1;
			}
			if (data[i] < tree[index])   // 如果数组内的值小于或等于树根，则与左子树比较
			{
				index = index * 2;
			}
			if (data[i] == tree[index])  // 如果数组内的值等于树根，则保持不变；并退出while循环，表示数组中该元素已经找到了其在BST中的位置
			{
				index = index;
				break;
			}
		}                                 // 如果子树节点的值不为0，则再与数组内的值比较一次
		tree[index] = data[i];            // 把数组值放入二叉树

		// 得到树中，节点的最大索引值
		if (index >= max_index)
		{
			max_index = index;
		}
	}
}

int GetLevel(int max_index)
{
	int level = 0;
	while ((pow(2, level) - 1) < max_index)
	{
		level++;
	}
	
	return level;
}

void LevelorderTraversal(int level, int tree[])
{
	// 按照行优先，且从左到右的顺序，打印输出二叉树的节点数据
	int node_num = (int)pow(2, level) - 1;        // 根据树的层数，得到树中节点的个数
	for (int i = 1; i <= node_num; i++)
	{
		cout << "[" << tree[i] << "] ";
	}
	cout << endl;
}

int main()
{
	int max_index = 1;                   // 存放树中，节点的最大的索引值
	int data[ArraySize] = { 6,3,5,3,9,7,8,4,2 };    // 原始数组
	int tree[16] = { 0 };                // 存放二叉树的数组，并初始化所有的16个元素都是0
	
	cout << "原始数组内容：" << endl;
	for (int i = 0; i < ArraySize; i++)
	{
		cout << "[" << data[i] << "] ";
	}	
	cout << endl;
	
	// 创建二叉搜索树且为满二叉树，缺省的元素用0来填补
	CreateTree(data, tree, max_index);   // 用一维数组来存储二叉搜索树中的元素

	int level = GetLevel(max_index);     // 根据树中，节点的最大索引值，获得树的层数

	cout << "二叉树搜索树内容：" << endl;
	LevelorderTraversal(level, tree);

	system("pause");
	return 0;
}

4.2 链表构建二叉搜索树，并完成增删查

? ? ? ? 所谓的链表表示法，实际上就是运用动态分配内存和指针的方式来建立二叉树，其中节点的数据结构包含了左子节点指针、数据和右子节点指针。

优点：增加和删除节点比较方便；

缺点：很难找到父节点，除非在每个节点的数据结构中增加一个父节点指针；

main.cpp

#include<iostream>
#include<queue>
#define ArraySize 9
using namespace std;

struct Node      // 二叉树节点数据结构的声明 
{ 
	int data;    // 节点数据
	Node* left;  // 指向左子树的指针
	Node* right; // 指向右子树的指针
};

// 将指定的值加入到二叉搜索树
void add(Node** rootNode, int data)
{
	//int flag = 0;            // 用来纪录是否插入新的节点

	// 建立节点内容
	Node* newnode = new Node;
	newnode->data = data;
	newnode->left = NULL;
	newnode->right = NULL;

	if (*rootNode == NULL)    // 如果为空的二叉搜索树，便将新的节点设定为根节点
	{ 
		*rootNode = newnode;
	}
	else
	{
		Node* currentNode = *rootNode;   // 指定一个指针指向根节点
		while (true)
		{
			if (data < currentNode->data)
			{ 
				// 当前节点的左节点存放比其数据小的节点
				if (currentNode->left == NULL)
				{
					currentNode->left = newnode;
					break;
				}
				else
				{
					// 当当前节点的左节点存放有数据时，要将左节点的重新作为当前节点并继续while循环
					currentNode = currentNode->left;
				}	
			}
			if (data > currentNode->data)
			{ 
				// 当前节点的右节点存放比其数据大的节点
				if (currentNode->right == NULL)
				{
					currentNode->right = newnode;
					break;
				}
				else
				{
					// 当当前节点的右节点存放有数据时，要将右节点的重新作为当前节点并继续while循环
					currentNode = currentNode->right;
				}
			}
			// 二叉搜索树，不能有相同键值的节点存在
			if (data == currentNode->data)
			{
				cout << data << " have been existed" << endl;
				break;
			}
		}	
	}
}

Node* Delete(Node* ptr, int val, int choice)  // choice==1（用中序先行者代替待删除的节点）或2（用中序后继者代替待删除的节点）
{
	if (ptr == NULL) { return ptr; }
	else
	{
		Node* tempNode1 = ptr;
		Node* pretempNode1 = ptr;
		while (true)
		{
			if (tempNode1->data > val) { pretempNode1 = tempNode1; tempNode1 = tempNode1->left; }
			if (tempNode1->data < val) { pretempNode1 = tempNode1; tempNode1 = tempNode1->right; }		
			// 找到了元素对应的BST中，节点的具体位置，即tempNode1指向的是待删除的节点
			if (tempNode1->data == val)
			{
				// 1、如果要删除的节点是BST中的叶子节点
				if (tempNode1->left == NULL && tempNode1->right == NULL)
				{
					if (pretempNode1->left->data == val)  // 要删除的节点是tempNode1的左叶子节点
					{
						delete pretempNode1->left;
						pretempNode1->left = nullptr;
						return ptr;
					}
					if (pretempNode1->right->data == val) // 要删除的节点是tempNode1的右叶子节点
					{
						delete pretempNode1->right;
						pretempNode1->right = nullptr;
						return ptr;
					}
				}

				// 2、如果要删除的节点只有一棵子树
				if (tempNode1->left == NULL && tempNode1->right != NULL)
				{
					tempNode1->data = tempNode1->right->data;
					delete tempNode1->right;
					tempNode1->right = nullptr;
					return ptr;
				}
				if (tempNode1->left != NULL && tempNode1->right == NULL)
				{
					tempNode1->data = tempNode1->left->data;
					delete tempNode1->left;
					tempNode1->left = nullptr;
					return ptr;
				}

				// 3、如果要删除的节点的有两棵子树时，有两种符合二叉搜索树的删除方式：   
				Node* tempNode2 = NULL;
				Node* pretempNode2 = NULL;
				if (tempNode1->left != NULL && tempNode1->right != NULL)
				{
					// 做法一：用中序立即先行者替换被删除的节点
					if (choice == 1)
					{
						pretempNode2 = tempNode1;
						tempNode2 = tempNode1->left;			
						while (tempNode2->right != NULL)
						{
							pretempNode2 = tempNode2;
							tempNode2 = tempNode2->right;
						}
						// 此时，tempNode2指向的是中序立即先行者/中序立即后继者
						tempNode1->data = tempNode2->data;
						delete pretempNode2->left;
						pretempNode2->left = nullptr;
						return ptr;
					}

					// 做法二：用中序立即后继者替换被删除的节点
					if (choice == 2)
					{
						pretempNode2 = tempNode1;
						tempNode2 = tempNode1->right;
						while (tempNode2->left != NULL)
						{
							pretempNode2 = tempNode2;
							tempNode2 = tempNode2->left;
						}
						// 此时，tempNode2指向的是中序立即先行者/中序立即后继者
						tempNode1->data = tempNode2->data;
						delete pretempNode2->right;
						pretempNode2->right = nullptr;
						return ptr;
					}				
				}
			}
		}
	}
}

// 查找二叉树某键值的函数
Node* search(Node* ptr, int val)
{
	while (true)
	{
		if (ptr == NULL) { return NULL; }
		if (ptr->data > val) { ptr = ptr->left; }
		if (ptr->data < val) { ptr = ptr->right; }
		if (ptr->data == val) { return ptr; }
	}
}

// 层序遍历
void LevelorderTraversal(Node* ptr)
{
	queue<Node*> output_queue;
	output_queue.push(ptr);
	output_queue.push(ptr->left);
	output_queue.push(ptr->right);

	cout << (output_queue.front())->data << " ";
	output_queue.pop();

	while (!output_queue.empty())
	{
		if ((output_queue.front())->left != NULL)
		{
			output_queue.push((output_queue.front())->left);
		}
		if ((output_queue.front())->right != NULL)
		{
			output_queue.push((output_queue.front())->right);
		}		
		cout << (output_queue.front())->data << " ";
		output_queue.pop();
	}
	cout << endl;
}

// 中序遍历
void InorderTraversal(Node* ptr)
{
	if (ptr != NULL)
	{
		InorderTraversal(ptr->left);
		cout << ptr->data << " ";
		InorderTraversal(ptr->right);
	}
}

// 前序遍历
void PreorderTraversal(Node* ptr)
{
	if (ptr != NULL)
	{
		cout << ptr->data << " ";
		PreorderTraversal(ptr->left);
		PreorderTraversal(ptr->right);
	}
}

// 后序遍历
void PostorderTraversal(Node* ptr)
{
	if (ptr != NULL)
	{
		PostorderTraversal(ptr->left);
		PostorderTraversal(ptr->right);
		cout << ptr->data << " ";
	}
}

int main()
{	
	// 用链表将一维数组中的数据存放到二叉搜索树中
	int arr[ArraySize] = { 6,3,5,9,7,3,8,4,2 };
	Node* rootNode = (Node*)malloc(sizeof(Node));   // 二叉搜索树的根节点的指针 
	rootNode = NULL;

	// 依据arr[]中的元素，构建二叉搜索树
	for (int i = 0; i < ArraySize; i++)
	{
		add(&rootNode, arr[i]);
	}

	// 找到BST中，与val有相同键值的节点，并打印其左右子节点的键值
	Node* tempNode = search(rootNode, 3);
	cout << tempNode->left->data << "->" << tempNode->data << "->" << tempNode->right->data << endl;

	cout << "level order print binary search tree" << endl;
	LevelorderTraversal(rootNode);
	cout << "inorder print binary search tree" << endl;
	InorderTraversal(rootNode);
	cout << endl;
	cout << "preorder print binary search tree" << endl;
	PreorderTraversal(rootNode);
	cout << endl;
	cout << "postorder print binary search tree" << endl;
	PostorderTraversal(rootNode);
	cout << endl;

	
	if (search(rootNode, 5) != NULL)
	{
		rootNode = Delete(rootNode, 5, 1);           // 删除的节点只有一个左子节点
		LevelorderTraversal(rootNode);
	}
	if (search(rootNode, 7) != NULL)
	{
		rootNode = Delete(rootNode, 7, 1);          // 删除的节点只有一个右子节点
		LevelorderTraversal(rootNode);
	}
	if (search(rootNode, 8) != NULL)
	{
		rootNode = Delete(rootNode, 8, 1);         // 删除的节点没有子节点
		LevelorderTraversal(rootNode);
	}
	if (search(rootNode, 3) != NULL)
	{
		rootNode = Delete(rootNode, 3, 2);
		LevelorderTraversal(rootNode);
	}

	system("pause");
	return 0;
}

五、中序线索二叉树

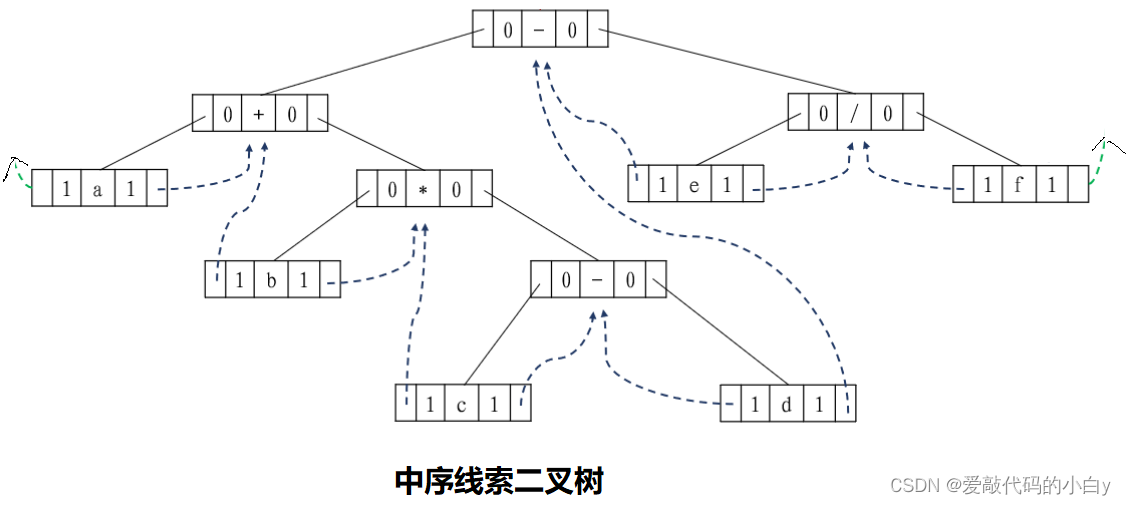
?????????线索二叉树，就是要利用这n+1个空链接来存放结点的前驱和后继结点的信息，即这些链接就是“线索”。最大的不同是，线索二叉树中每个结点需要另外加入两个整型数据位LBIT、RBIT（正常指针用0填充、线索用1填充），用来识别左右子树指针是 正常的链接指针 还是 线索（线索用虚线、正常的链接用实线）。

????????将二叉树转换为中序线索二叉树，步骤：

• 先将二叉树经由中序遍历方式按序排列，并将所有空链接改成线索；
• 如果线索链接是指向该节点的左指针，则将该线索指向中序遍历下的前一个结点；
• 如果线索链接是指向该节点的右指针，则将该线索指向中序遍历下的后一个结点；?

代码分析：重点是删除元素的操作，代码实现按照下图的思路：

?ThreadBST.hpp

#pragma once
#include <iostream>
#include <iomanip>
using namespace std;

// 线索二叉树：当两个左（右）节点指针是线索时，左（右）节点指向前驱（后继）一个节点
// 二叉搜索树与线索二叉树的合并，在插入与删除的同时维护了前序和后序的关系
template<class T>
class Node
{
public:
	// 给构造函数默认值，当构造Node对象时，给参数列表默认的参数即可
	Node(const T& init_data = T()) : data(init_data) { }

	T data;
	Node* parent = NULL;
	Node* left = NULL;
	Node* right = NULL;
	int left_flag = 0;   // flag==0表示该节点有正常的左（右）子树 ，即存在左（右）子节点；flag==1表示该节点左（右）节点不存在，指向的该节点的中序先行者/中序后继者
	int right_flag = 0;
};

template<class T>
class ThreadBST
{
public:
	ThreadBST() { head = NULL; }
	~ThreadBST() { cout << "执行了析构函数~ThreadBST()" << endl; clear(head); }

	Node<T>* GetRootNode() { return head; }

	void Insert(T data);              // 二叉搜索树插入结点,并维护已有的中序线索 

	Node<T>* Find(T data);            // 二叉搜索树查询一个元素，并返回指向该元素的指针 

	void Delete(T data, int choice);               // 清除一个元素 

	void InorderTraversal();                       // 进行中序遍历 

private:
	Node<T>* head;
	void clear(Node<T>* root);               // 用于析构函数中，来清楚threadBST中的各个节点的数据并释放整个内存空间
	Node<T>* InorderPreNode(Node<T>* ptr);   // 查找该指针指向元素的中序先行者 
	Node<T>* InorderNextNode(Node<T>* ptr);  // 查找该指针指向元素的中序后继者 
};


template<class T>
void ThreadBST<T>::clear(Node<T>* root)
{
	if (root == NULL) { return; }    // 作为递归的返回条件
	if (root != NULL)
	{
		if (root->left_flag == 0 && root->left != NULL)    // root指向的节点有正常的左子树
		{
			clear(root->left);
		}
		if (root->right_flag == 0 && root->right != NULL)  // root指向的节点有正常的右子树
		{
			clear(root->right);
		}
		delete root;
		root = nullptr;
	}
}

template<class T>
void ThreadBST<T>::Insert(T data)
{
	Node<T>* newNode = new Node<T>(data);

	if (head == NULL)
	{
		head = newNode;
		return;
	}

	Node<T>* tempNode = head;
	while (true)
	{
		// 找到该threadBST树中，右下的节点，直到不满足条件
		if (data > tempNode->data)
		{
			while (data > tempNode->data && tempNode->right_flag == 0 && tempNode->right != NULL)
			{
				tempNode = tempNode->right;
			}
			// 此时，tempNode指向的 newNode指针指向的data所在节点的父节点；
			// 此时data > tempNode->data，则newNode插入到tempNode的右子节点；否则data<temp->data，则跳到if (data < tempNode->data)；否则data==temp->data，则跳到if (data == tempNode->data)；
			if (data > tempNode->data)
			{
				// 重点！！！    tempNode节点的右子节点newNode，继承了tempNode->right、tempNode->right_flag的状态
				newNode->right = tempNode->right; newNode->right_flag = tempNode->right_flag;

				newNode->left = tempNode; newNode->left_flag = 1;
				tempNode->right = newNode; tempNode->right_flag = 0;

				newNode->parent = tempNode;
				return;
			}
		}
		if (data < tempNode->data)
		{
			// 找到该threadBST树中，左下的节点，直到不满足条件
			while (data < tempNode->data && tempNode->left_flag == 0 && tempNode->left != NULL)
			{
				tempNode = tempNode->left;
			}
			// 此时，tempNode指向的 data未来位置的父节点
			// 此时data<temp->data，则newNode插入到tempNode的左子节点；否则data > tempNode->data，则跳到if (data > tempNode->data)；否则data==temp->data，则跳到if (data == tempNode->data)；
			if (data < tempNode->data)
			{
				// 重点！！！    tempNode节点的左子节点newNode，继承了tempNode->left、tempNode->left_flag的状态
				newNode->left = tempNode->left; newNode->left_flag = tempNode->left_flag;

				newNode->right = tempNode; newNode->right_flag = 1;
				tempNode->left = newNode; tempNode->left_flag = 0;

				newNode->parent = tempNode;
				return;
			}
		}
		if (data == tempNode->data)
		{
			cout << "data=" << data << "对应键值的节点已经存在在threadBST树中了" << endl;
			return;
		}
	}
}

template<class T>
Node<T>* ThreadBST<T>::InorderPreNode(Node<T>* ptr)
{
	// 被查找的节点的左节点没有左子树，故其中序先行者是通过线索直接找到
	if (ptr->left_flag == 1)
	{
		return ptr->left;
	}
	// 被查找的节点的左节点有左子树，故中序先行者是 左二叉搜索子树的最大值
	else
	{
		Node<T>* tempNode = ptr->left;   // 该节点左子树的根节点
		// 找到左子树中最右下的节点，即左子树中元素的最大值所在的节点
		while (tempNode->right_flag == 0 && tempNode->right != NULL)
		{
			tempNode = tempNode->right;
		}
		return tempNode;
	}
}

template<class T>
Node<T>* ThreadBST<T>::InorderNextNode(Node<T> *ptr)
{
	// 被查找的节点的左节点没有右子树，故其中序后继者是通过线索直接找到
	if (ptr->right_flag == 1)
	{
		return ptr->right;
	}
	// 被查找的节点的左节点有右子树，故中序后继者是 右二叉搜索子树的最小值
	else
	{
		Node<T>* tempNode = ptr->right;
		// 找到右子树中最左下的节点，即右子树中元素的最小值所在的节点
		while (tempNode->left_flag == 0 && tempNode->left != NULL)
		{
			tempNode = tempNode->left;
		}
		return tempNode;
	}
}

template<class T>
Node<T>* ThreadBST<T>::Find(T data)
{
	Node<T>* tempNode = head;
	while (true)
	{
		while (data > tempNode->data && tempNode->right_flag == 0 && tempNode->right != NULL)
		{
			tempNode = tempNode->right;
		}
		if (data > tempNode->data)   // 此时，tempNode是线索二叉搜索树中最大的节点
		{
			// 当data比threadBST中最大的元素还大时，表示data不在threadBST中
			cout << "This node is not in the tree" << endl;
			return NULL;
			break;
		}
		while (data < tempNode->data && tempNode->left_flag == 0 && tempNode->left != NULL)
		{
			tempNode = tempNode->left;
		}
		if (data < tempNode->data)  // 此时，tempNode是线索二叉搜索树中最小的节点
		{
			// 当data比threadBST中最小的元素还小时，表示data不在threadBST中
			cout << "This node is not in the tree" << endl;
			return NULL;
			break;
		}
		if (data == tempNode->data)
		{
			return tempNode;
		}
	}
}

// 树的删除操作，分三种情况：
// 1）无子节点；2）有一个子树，分四种情况讨论；
// 3）有两个子树，有两种删法（①用该节点对应的左子树的中序先行者替换该节点；②用该节点对应的右子树的中序后继者替换该节点），从而转化为 1）和 2）情况
template<class T>
void ThreadBST<T>::Delete(T data, int choice)
{
	Node<T>* node = Find(data);
	if (node == NULL) { return; }

	Node<T> *pre = InorderPreNode(node);
	Node<T> *next = InorderNextNode(node);

	// node有两个子树
	if (node->left_flag == 0 && node->left != NULL && node->right_flag == 0 && node->right != NULL)
	{
		// 有两种删法：1）用该节点对应的左子树的中序先行者替换该节点；2）用该节点对应的右子树的中序后继者替换该节点
		if (choice == 1)
		{
			node->data = pre->data;
			node = pre;     // 转换要删除的目标节点
			pre = InorderPreNode(node);
			next = InorderNextNode(node);
		}
		else
		{
			node->data = next->data;
			node = next;    // 转换要删除的目标节点
			pre = InorderPreNode(node);
			next = InorderNextNode(node);
		}
	}
	// node无任何子结点
	if ((node->left_flag == 1 && node->right_flag == 1) || (node->left_flag == 1 && node->right == NULL) || (node->left == NULL && node->right_flag == 1))
	{
		// 待删除的节点是其父节点的右子节点
		if (pre->right == node)
		{
			pre->right = next; pre->right_flag = 1;
		}

		// 待删除的节点是其父节点的左子节点
		if (next->left == node)
		{
			next->left = pre; next->left_flag = 1;
		}
	}
	// node有一个子树：直接用待删除节点的前驱/后继节点，代替待删除的节点即可
	else
	{
		Node<T> *father = node->parent;
		// 待删除的节点在其父节点的左子树
		if (father->left == node)
		{
			// 待删除的节点的左子节点存在
			if (node->left_flag == 0 && node->left != NULL)
			{
				father->left = node->left;
				(node->left)->parent = father;

				// 找到待删除的node节点左子树中，中序后继节点指向node节点的节点tempNode
				Node<T>* tempNode = node->left;  // 此时，tempNode指向的是待删除节点node左子树的根节点
				while (tempNode->right_flag == 0)
				{
					tempNode = tempNode->right;
				}
				tempNode->right = father;
			}
			// 待删除的节点的右子节点存在
			else if (node->right_flag == 0 && node->right != NULL)
			{
				father->left = node->right;
				(node->right)->parent = father;

				// 找到待删除的node节点右子树中，中序先行节点指向node节点的节点tempNode
				Node<T>* tempNode = node->right;  // 此时，tempNode指向的是待删除节点node右子树的根节点
				while (tempNode->left_flag == 0)
				{
					tempNode = tempNode->left;
				}
				tempNode->left = pre;
			}
		}
		// 待删除的节点在其父节点的右子树
		if (father->right == node)
		{
			// 待删除的节点的左子节点存在
			if (node->left_flag == 0 && node->left != NULL) 
			{
				father->right = node->left;
				(node->left)->parent = father;

				// 找到待删除的node节点左子树中，中序后继节点指向node节点的节点tempNode
				Node<T>* tempNode = node->left;   // 此时，tempNode指向的是待删除节点node左子树的根节点
				while (tempNode->right_flag == 0)
				{
					tempNode = tempNode->right;
				}
				tempNode->right = next;
			}
			// 待删除的节点的右子节点存在
			else if (node->right_flag == 0 && node->right != NULL)  
			{
				father->right = node->right;
				(node->right)->parent = father;

				// 找到待删除的node节点右子树中，中序先行节点指向node节点的节点tempNode
				Node<T>* tempNode = node->right;  // 此时，tempNode指向的是待删除节点node右子树的根节点
				while (tempNode->left_flag == 0)
				{
					tempNode = tempNode->left;
				}
				tempNode->left = father;
			}
		}
	}
	delete node; node = nullptr;
	return;
}

// 二叉树中序遍历
template<class T>
void ThreadBST<T>::InorderTraversal()
{
	if (head == NULL) { return; }

	/*中序遍历：先打印左子树，后打印右子树*/ 

	// 先找到threadBST树中，最左下的节点
	Node<T>* tempNode = head;
	while (tempNode->left_flag == 0 && tempNode->left != NULL)
	{
		tempNode = tempNode->left;
	}
	cout << tempNode->data << " ";   // 此时，tempNode指向的是树中最左下的节点

	// threadBST树中，只有最大键值对应的节点（即树的最右下角对应的节点）的tempNode->right==NULL
	while (tempNode->right != NULL) 
	{
		// 如果tempNode指向的节点存在右节点（即right_flag==0），则直接指向右子树；	
		if (tempNode->right_flag == 0)
		{
			tempNode = tempNode->right;
			// tempNode指向的节点的左节点存在，不断进入while循环；除非左节点不存在，则直接打印输出数据，然后通过线索指向中序后继节点
			while (tempNode->left_flag == 0)
			{
				tempNode = tempNode->left;
			}
		}
		// 不存在右节点（即right_flag==1），则通过线索指向中序后继节点
		else
		{
			tempNode = tempNode->right;
		}
		cout << tempNode->data << " ";
	}
	cout << endl;
}

main.cpp

#include "ThreadBST.hpp"

int main()
{
	ThreadBST<int>* threadBST = new ThreadBST<int>;
	int array_size = 15;
	int data[] = { 10,400,20,6,8,5,3,500,100,399,453,43,237,373,655 };
	for (int i = 0; i < array_size; i++)
	{
		threadBST->Insert(data[i]);
	}
	// 构建threadBST线索二叉搜索树时，最小的和最大的节点分别对应的节点的左子节点指针、右子节点指针指向的时NULL
	cout << "inorder traversal："; threadBST->InorderTraversal();

	cout << "删除带有0个子节点的节点：" << endl; threadBST->Delete(43, 2);      // 删除带有无个子节点的节点
	cout << "inorder traversal："; threadBST->InorderTraversal();

	cout << "删除带有两个子节点的节点：" << endl; threadBST->Delete(10, 2);      // 删除带有两个子节点的节点
	cout << "inorder traversal："; threadBST->InorderTraversal();

	cout << "删除带有一个右子节点的节点：" << endl; threadBST->Delete(399, 2);   // 删除带有一个左子节点的节点
	cout << "inorder traversal："; threadBST->InorderTraversal();

	cout << "删除带有一个左子节点的节点：" << endl; threadBST->Delete(237, 2);   // 删除带有一个右子节点的节点
	cout << "inorder traversal："; threadBST->InorderTraversal();



	delete threadBST;
	threadBST = nullptr;         

	return 0;
}

六、构建平衡二叉树AVL

对于平衡二叉树，其实是二叉搜索树的进阶版，在二叉搜索树的前提条件下，要满足左右子树的高度差小于1的情况。这种平衡性在进行插入和删除操作，就很容易被破坏，这是就需要通过“树的旋转”来修复造成二叉树不平衡的结点，此时树至少需要在三层或者以上。

6.1 树的旋转：

图示为四种树旋转的形式：LL型、LR型、RR型、RL型。

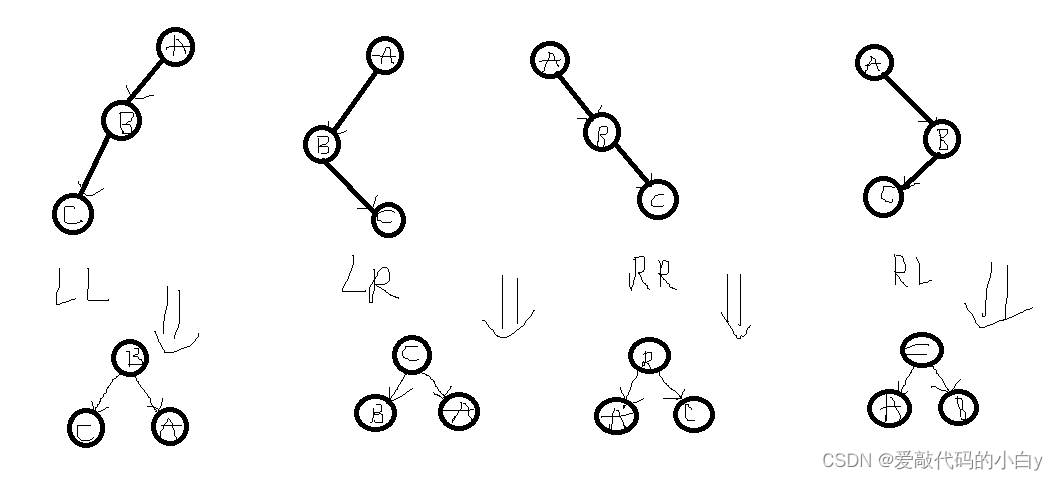
LL型的调整，其待调整的节点A的平衡因子（左右子树的高度差）为阴影部分，一旦阴影部分的高度大于0则会造成不平衡A节点的左右子树不平衡，故需要下降A节点的层级并用B节点来填补，将B节点的右子树，传给A的左子树，这样在不破坏二叉搜索树的特性下，将其调整为平衡二叉树。

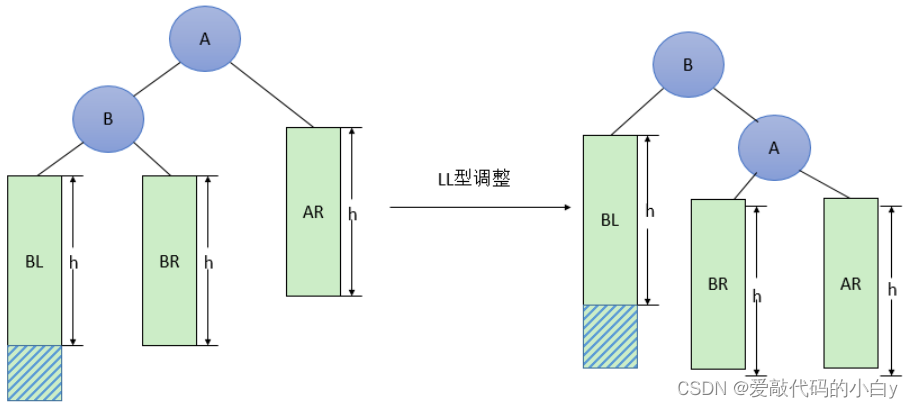?代码实现：

int max(int a, int b) 
{
    return (a > b) ? a : b;
}

template<class T>
AVLNode<T>* AVLTree<T>::ll_rotate(AVLNode<T>* y)   // y是待调整的节点
{
	AVLNode<T>* x = y->left;
	y->left = x->right;
	x->right = y;

	y->height = max(GetHeight(y->left), GetHeight(y->right)) + 1;
	x->height = max(GetHeight(x->left), GetHeight(x->right)) + 1;

	return x;
}

RR型的调整，其待调整的节点A的平衡因子（左右子树的高度差）为阴影部分，一旦阴影部分的高度大于0则会造成不平衡A节点的左右子树不平衡，故需要下降A节点的层级并用B节点来填补，将B节点的左子树，传给A的右子树，这样在不破坏二叉搜索树的特性下，将其调整为平衡二叉树。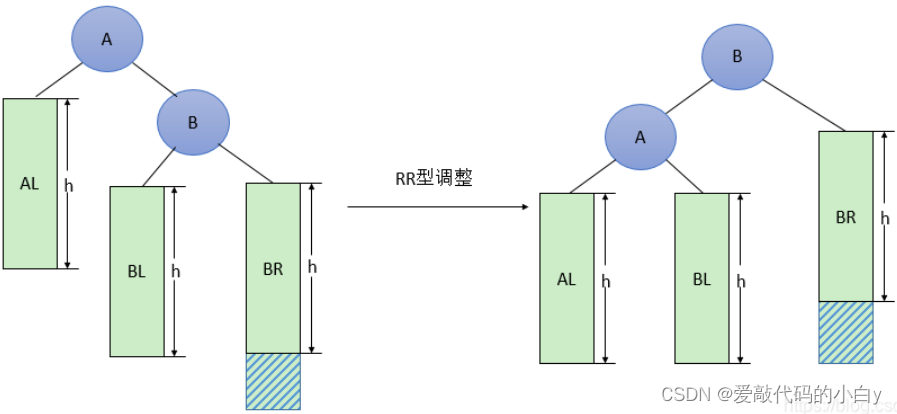

??代码实现：

int max(int a, int b) 
{
    return (a > b) ? a : b;
}

template<class T>
AVLNode<T>* AVLTree<T>::rr_rotate(AVLNode<T>* y)  // y是待调整的节点
{
	AVLNode<T>* x = y->right;
	y->right = x->left;
	x->left = y;

	y->height = max(GetHeight(y->left), GetHeight(y->right)) + 1;
	x->height = max(GetHeight(x->left), GetHeight(x->right)) + 1;

	return x;
}

LR型的调整，其待调整的节点A的平衡因子（左右子树的高度差）为阴影部分中max{h_shadow} + 1，一旦阴影部分的最大高度max{h_shadow}大于0则会造成不平衡A节点的左右子树不平衡，故需要下降A节点的层级并用C节点来填补，将C节点的右子树传给A的右子树，C节点的左子树传给B的右子树，这样在不破坏二叉搜索树的特性下，将其调整为平衡二叉树。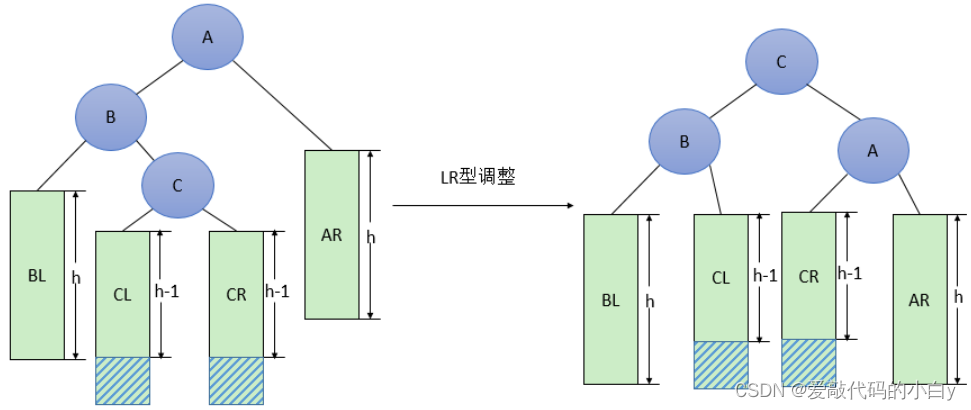

?分步实现过程：LR == RR + LL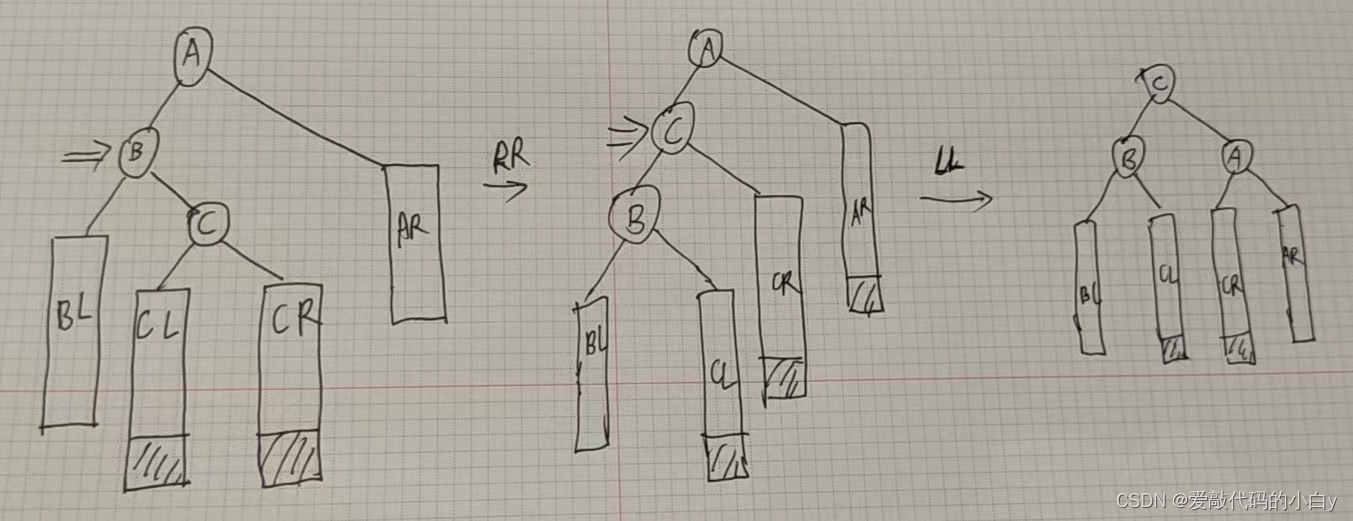

??代码实现：

template<class T>
AVLNode<T>* AVLTree<T>::lr_rotate(AVLNode<T>* y)
{
	// LR == RR + LL
	AVLNode<T>* x = y->left;
	y->left = rr_rotate(x);
	return ll_rotate(y);
}

RL型的调整，其待调整的节点A的平衡因子（左右子树的高度差）为阴影部分中max{h_shadow} + 1，一旦阴影部分的最大高度max{h_shadow}大于0则会造成不平衡A节点的左右子树不平衡，故需要下降A节点的层级并用C节点来填补，将C节点的左子树传给A的左子树，C节点的右子树传给B的左子树，这样在不破坏二叉搜索树的特性下，将其调整为平衡二叉树。

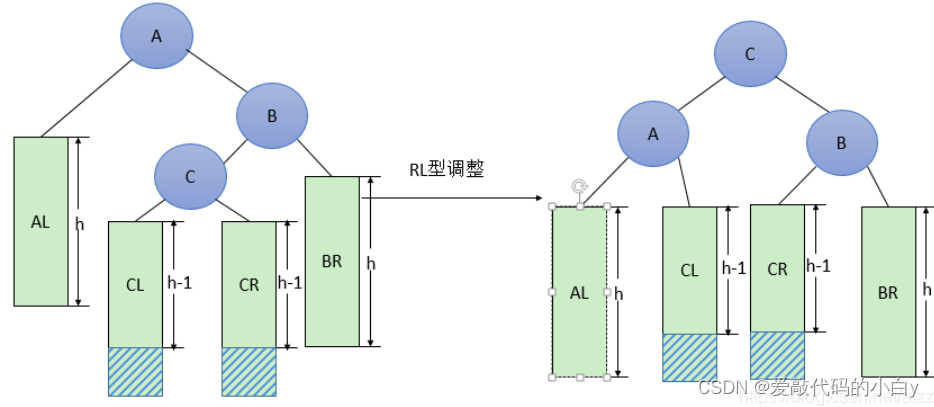
??分步实现过程：LR == LL + RR

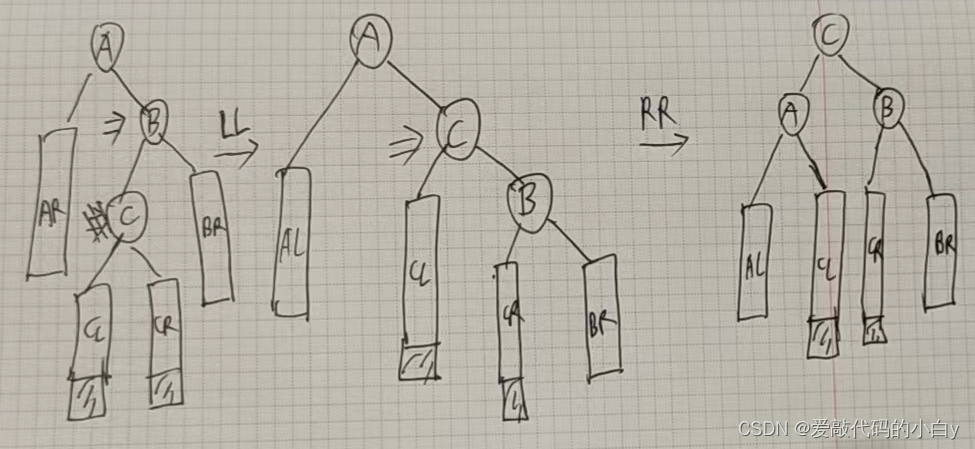
???代码实现：

template<class T>
AVLNode<T>* AVLTree<T>::rl_rotate(AVLNode<T>* y)
{
	// RL == LL + RR
	AVLNode<T>* x = y->right;
	y->right = ll_rotate(x);
	return rr_rotate(y);
}

通过代码用一个数组arr[] = { 9, 5, 10, 0, 6, 11, -1, 1, 2 }，来初始化平衡二叉树；并通过不断的插入和删除过程中，利用树的旋转保持二叉树满足平衡二叉树的特性。

6.2 插入过程的分析：

（插入数据的过程中与二叉搜索树相似，这里重点是插入后的调整的部分），插入后由于插入位置的父节点满足平衡因子不大于1，故会不断回溯到爷爷节点的位置，从而爷爷、父节点和插入的位置形成了上述LL、RR、LR、RL型的关系，并调整即可；

template<class T>
AVLNode<T>* AVLTree<T>::insert(AVLNode<T>* node, T& data)  // 每次最初传入的node节点都是平衡二叉树的根节点this->root，返回的是插入元素并调整后平衡二叉树的根节点
{
	/* 1、将data元素作为节点插入到平衡二叉树中 */
	// 当传入的节点node是空节点时，需要申请内存空间来存储数据data
	if (node == NULL)                 // insert()函数，递归结束的出口
	{
		node =  new AVLNode<T>(data);
		node->height = 1;
		return node;
	}

	// 将待插入的数据与该节点的键值进行比较，决定要将其插入到哪个位置？
	if (data < node->data)
	{
		node->left = insert(node->left, data);
	}		
	else if (data > node->data)
	{
		node->right = insert(node->right, data);
	}
	else
	{
		cout << node << "have existed inside the AVL tree" << endl;
		return node;
	}

	// 此时，node代表的是待插入元素data的父节点的父节点
	node->height = max(GetHeight(node->left), GetHeight(node->right)) + 1;  // 调整平衡该节点的高度：左右子树中高度的最大值 + 1
	
	/* 2、根据插入后树的状态，进行调整使平衡二叉树的特性均得到满足（-1 < 左右节点的平衡因子 < 1）*/
	// 得到待插入元素data的父节点的父节点node的平衡因子：左右子树的高度差
	int bf = GetBalanceFactor(node);
	if (bf > 1 && data < node->left->data) { return ll_rotate(node); }      // LL型	
	if (bf < -1 && data > node->right->data) { return rr_rotate(node); }    // RR型
	if (bf > 1 && data > node->left->data) { return lr_rotate(node); }      // LR型
	if (bf < -1 && data < node->right->data) { return rl_rotate(node); }    // RL型

	return node;
}

6.3 删除过程（难点！！！）的分析：

（删除数据的过程与二叉搜索树相似，这里重点是删除后的调整的部分），具体体现在删除后，不断回溯找到平衡因子的绝对值大于1的情况，即bf > 1或者bf < -1，此时判断采用四种旋转方式中的哪一种(即b1 > 1: LL或者LR; b1 < -1: RL或者RR)，其中bf > 1：{ bf_left >= 0：LL、bf_left < 0：LR } 和 bf < -1：{ bf_right >= 0：RL、bf_right < 0：RR }

template<class T>
AVLNode<T>* AVLTree<T>::minValueSubNode(AVLNode<T>* node)  // 返回以node为子树的根节点，并找到左右子树的中最小键值对应的元素
{
	AVLNode<T>* current = node;
	while (current->left != NULL)
	{
		current = current->left;
	}
	return current;
}

template<class T>
AVLNode<T>* AVLTree<T>::deleteNode(AVLNode<T>* root, T& data)
{
	// root为空时，直接返回
	if (root == NULL) { return root; }

	/* 1、先删除data所在的节点 */ 
	if (data == root->data)
	{	
		// 1、root节点的左右子节点，不全存在
		if ((root->left == NULL) || (root->right == NULL))
		{
			// root的左右子节点中全部为空
			if ((root->left == NULL) && (root->right == NULL))
			{
				delete root;
				return NULL;
			}
			// root的左右子节点有且只有一个为空
			else
			{ 
				// 找到root的左子节点和右子节点中不为空哪个不为空，则用temp指向它
				AVLNode<T>* temp = root->left ? root->left : root->right;
				delete root;
				return temp;
			}
		}
		// 2、root节点的左右子节点，全存在，即要删除的root节点需要用root右子树中的最小的节点代替
		else
		{
			// 找到root节点右子树中的最小的节点，用来替代root节点
			AVLNode<T>* temp = minValueSubNode(root->right);
			root->data = temp->data;
			// 重新以root节点的右节点作为根节点，来删除temp（用来代替root节点的节点）
			root->right = deleteNode(root->right, temp->data);
		}
	}
	else if (data < root->data)
	{
		root->left = deleteNode(root->left, data);
	}
	else      // data > root->data
	{
		root->right = deleteNode(root->right, data);
	}

	if (root == NULL) { return root; }   // root为空时，直接返回
	root->height = max(GetHeight(root->left), GetHeight(root->right)) + 1;   // 调整平衡该节点的高度：左右子树中高度的最大值 + 1
	
	// 删除完成后，会不断回溯直到找到出现平衡因子的绝对值不小于1的情况，即要以该节点作为根节点进行树的旋转直到达到树的平衡
	/* 调整整个二叉树的状态，使其满足平衡二叉树的所有特性 */ 	
	int bf = GetBalanceFactor(root);
	int bf_left = GetBalanceFactor(root->left);
	int bf_right = GetBalanceFactor(root->right);
	if (bf > 1 && bf_left >= 0) { cout << "LL" << endl; return ll_rotate(root); }    // LL型	
	if (bf > 1 && bf_left < 0) { cout << "LR" << endl; return lr_rotate(root); }   // LR型
	if (bf < -1 && bf_right >= 0) { cout << "RL" << endl; return rl_rotate(root); }   // RL型
	if (bf < -1 && bf_right < 0) { cout << "RR" << endl; return rr_rotate(root); }    // RR型
	return root;
}

完整代码：

#include<iostream>
#include<queue>
using namespace std;

template<class T>
class AVLNode
{
public:
	AVLNode() : left(NULL), right(NULL), height(1) {}
	AVLNode(T data, AVLNode<T>* left = NULL, AVLNode<T>* right = NULL, int height = 1) : data(data), left(left), right(right), height(height) {}

	int data;
	AVLNode<T>* left;
	AVLNode<T>* right;
	int height;
};

template<class T>
class AVLTree
{
public: 
	AVLTree() : root(NULL) {}                     // 调用无参构造函数，创建的平衡二叉树的 根节点为空  
	AVLTree(T data) : root(new AVLNode<T>(data)) {}  // 根据数据创建AVLTree树的根节点    
	AVLTree(T* arr, int size);                    // 根据数组创建平衡二叉树AVLTree
	~AVLTree() { this->clear(this->root); this->root = nullptr; }

	AVLNode<T>* GetRoot() { return this->root; }
	int GetHeight(AVLNode<T>* node);

	// 四种树的旋转类型：LL、RR、LR、RR型
	AVLNode<T>* ll_rotate(AVLNode<T>* y);
	AVLNode<T>* rr_rotate(AVLNode<T>* y);
	AVLNode<T>* lr_rotate(AVLNode<T>* y);
	AVLNode<T>* rl_rotate(AVLNode<T>* y);

	// 得到节点的平衡因子，即左右子树的高度差
	int GetBalanceFactor(AVLNode<T>* node);

	void Insert(T& key) { this->root = this->insert(this->root, key); }
	AVLNode<T>* minValueSubNode(AVLNode<T>* node);
	void DeleteNode(T key) { this->root = this->deleteNode(this->root, key); }

	// 四种树的遍历方式
	void PreOrderTraversal() { this->preOrder(this->root); cout << endl; }
	void InOrderTraversal() { this->inOrder(this->root); cout << endl; }
	void PostOrderTraversal() { this->postOrder(this->root); cout << endl; }
	void LevelOrderTraversal() { this->levelOrderTraversal(); }
private:
	AVLNode<T>* root;
	int max(int a, int b) { return (a > b) ? a : b; }

	AVLNode<T>* insert(AVLNode<T>* node, T& key);
	AVLNode<T>* deleteNode(AVLNode<T>* node, T& key);
	AVLNode<T>* Balance(AVLNode<T>* root);

	void preOrder(AVLNode<T>* root);
	void inOrder(AVLNode<T>* root);
	void posrOrder(AVLNode<T>* root);
	void levelOrderTraversal();

	void clear(AVLNode<T>* node);
};

template<class T>
AVLTree<T>::AVLTree(T* arr, int size)             
{
	for (int i = 0; i < size; i++)
	{
		this->Insert(arr[i]);
	}
}

template<class T>
void AVLTree<T>::clear(AVLNode<T>* node)
{
	if (node == NULL)
	{
		return;
	}
	if (node->left != NULL)
	{
		clear(node->left);
	}
	if (node->right != NULL)
	{
		clear(node->right);
	}
	delete node;
	node = nullptr;
}

template<class T>
void AVLTree<T>::preOrder(AVLNode<T>* root)
{
	if (root != NULL)
	{
		cout << root->data << " ";
		preOrder(root->left);
		preOrder(root->right);
	}
}
template<class T>
void AVLTree<T>::inOrder(AVLNode<T>* root)
{
	if (root != NULL)
	{
		inOrder(root->left);
		cout << root->data << " ";
		inOrder(root->right);
	}
}
template<class T>
void AVLTree<T>::posrOrder(AVLNode<T>* root)
{
	if (root != NULL)
	{
		postOrder(root->left);
		postOrder(root->right);
		cout << root->data << " ";
	}
}
template<class T>
void AVLTree<T>::levelOrderTraversal()
{
	queue<AVLNode<T>*> queue;
	AVLNode<T>* temp = this->root;
	queue.push(temp);
	while (!queue.empty())
	{
		temp = queue.front(); queue.pop();
		cout << temp->data << " ";

		if (temp->left != NULL)
		{
			queue.push(temp->left);
		}
		if (temp->right != NULL)
		{
			queue.push(temp->right);
		}
	}
	cout << endl;
}

template<class T>
int AVLTree<T>::GetHeight(AVLNode<T>* node)
{
	if (node == NULL)
	{
		return 0;
	}
	return node->height;
}

template<class T>
int AVLTree<T>::GetBalanceFactor(AVLNode<T>* node)
{
	if (node == NULL)
	{
		return 0;
	}

	return GetHeight(node->left) - GetHeight(node->right);
}


template<class T>
AVLNode<T>* AVLTree<T>::ll_rotate(AVLNode<T>* y)
{
	AVLNode<T>* x = y->left;
	y->left = x->right;
	x->right = y;

	y->height = max(GetHeight(y->left), GetHeight(y->right)) + 1;
	x->height = max(GetHeight(x->left), GetHeight(x->right)) + 1;

	return x;
}
template<class T>
AVLNode<T>* AVLTree<T>::rr_rotate(AVLNode<T>* y)
{
	AVLNode<T>* x = y->right;
	y->right = x->left;
	x->left = y;

	y->height = max(GetHeight(y->left), GetHeight(y->right)) + 1;
	x->height = max(GetHeight(x->left), GetHeight(x->right)) + 1;

	return x;
}
template<class T>
AVLNode<T>* AVLTree<T>::lr_rotate(AVLNode<T>* y)
{
	// LR == RR + LL
	AVLNode<T>* x = y->left;
	y->left = rr_rotate(x);
	return ll_rotate(y);
}
template<class T>
AVLNode<T>* AVLTree<T>::rl_rotate(AVLNode<T>* y)
{
	// RL == LL + RR
	AVLNode<T>* x = y->right;
	y->right = ll_rotate(x);
	return rr_rotate(y);
}

template<class T>
AVLNode<T>* AVLTree<T>::insert(AVLNode<T>* node, T& data)  // 每次最初传入的node节点都是平衡二叉树的根节点this->root，返回的是插入元素并调整后平衡二叉树的根节点
{
	/* 1、将data元素作为节点插入到平衡二叉树中 */
	// 当传入的节点node是空节点时，需要申请内存空间来存储数据data
	if (node == NULL)                 // insert()函数，递归结束的出口
	{
		node =  new AVLNode<T>(data);
		node->height = 1;
		return node;
	}

	// 将待插入的数据与该节点的键值进行比较，决定要将其插入到哪个位置？
	if (data < node->data)
	{
		node->left = insert(node->left, data);
	}		
	else if (data > node->data)
	{
		node->right = insert(node->right, data);
	}
	else
	{
		cout << node << "have existed inside the AVL tree" << endl;
		return node;
	}

	// 此时，node代表的是待插入元素data的父节点的父节点
	node->height = max(GetHeight(node->left), GetHeight(node->right)) + 1;  // 调整平衡该节点的高度：左右子树中高度的最大值 + 1
	
	/* 2、根据插入后树的状态，进行调整使平衡二叉树的特性均得到满足（-1 < 左右节点的平衡因子 < 1）*/
	// 得到待插入元素data的父节点的父节点node的平衡因子：左右子树的高度差
	int bf = GetBalanceFactor(node);
	if (bf > 1 && data < node->left->data) { return ll_rotate(node); }      // LL型	
	if (bf < -1 && data > node->right->data) { return rr_rotate(node); }    // RR型
	if (bf > 1 && data > node->left->data) { return lr_rotate(node); }      // LR型
	if (bf < -1 && data < node->right->data) { return rl_rotate(node); }    // RL型

	return node;
}

template<class T>
AVLNode<T>* AVLTree<T>::minValueSubNode(AVLNode<T>* node)  // 返回以node为子树的根节点，并找到左右子树的中最小键值对应的元素
{
	AVLNode<T>* current = node;
	while (current->left != NULL)
	{
		current = current->left;
	}
	return current;
}

template<class T>
AVLNode<T>* AVLTree<T>::deleteNode(AVLNode<T>* root, T& data)
{
	// root为空时，直接返回
	if (root == NULL) { return root; }

	/* 1、先删除data所在的节点 */ 
	if (data == root->data)
	{	
		// 1、root节点的左右子节点，不全存在
		if ((root->left == NULL) || (root->right == NULL))
		{
			// root的左右子节点中全部为空
			if ((root->left == NULL) && (root->right == NULL))
			{
				delete root;
				return NULL;
			}
			// root的左右子节点有且只有一个为空
			else
			{ 
				// 找到root的左子节点和右子节点中不为空哪个不为空，则用temp指向它
				AVLNode<T>* temp = root->left ? root->left : root->right;
				delete root;
				return temp;
			}
		}
		// 2、root节点的左右子节点，全存在，即要删除的root节点需要用root右子树中的最小的节点代替
		else
		{
			// 找到root节点右子树中的最小的节点，用来替代root节点
			AVLNode<T>* temp = minValueSubNode(root->right);
			root->data = temp->data;
			// 重新以root节点的右节点作为根节点，来删除temp（用来代替root节点的节点）
			root->right = deleteNode(root->right, temp->data);
		}
	}
	else if (data < root->data)
	{
		root->left = deleteNode(root->left, data);
	}
	else      // data > root->data
	{
		root->right = deleteNode(root->right, data);
	}

	if (root == NULL) { return root; }   // root为空时，直接返回
	root->height = max(GetHeight(root->left), GetHeight(root->right)) + 1;   // 调整平衡该节点的高度：左右子树中高度的最大值 + 1
	
	// 删除完成后，会不断回溯直到找到出现平衡因子的绝对值不小于1的情况，即要以该节点作为根节点进行树的旋转直到达到树的平衡
	/* 调整整个二叉树的状态，使其满足平衡二叉树的所有特性 */ 	
	int bf = GetBalanceFactor(root);
	int bf_left = GetBalanceFactor(root->left);
	int bf_right = GetBalanceFactor(root->right);
	if (bf > 1 && bf_left >= 0) { cout << "LL" << endl; return ll_rotate(root); }    // LL型	
	if (bf > 1 && bf_left < 0) { cout << "LR" << endl; return lr_rotate(root); }   // LR型
	if (bf < -1 && bf_right >= 0) { cout << "RL" << endl; return rl_rotate(root); }   // RL型
	if (bf < -1 && bf_right < 0) { cout << "RR" << endl; return rr_rotate(root); }    // RR型
	return root;
}


int main()
{
	/* The constructed AVL Tree would be
				    8
				 /     \
			   5        10
			 /  \      /  \
			0    6    9    11
		   / \     \         \  
		  -1  1     7         12
		       \
			    2
	*/
	int arr[] = { 8, 9, 5, 10, 0, 6, 7, 11, 12, -1, 1, 2 };
	int size = sizeof(arr) / sizeof(arr[0]);
	AVLTree<int> avltree(arr, size);
	AVLNode<int>* root = avltree.GetRoot();
	printf("前序遍历："); avltree.PreOrderTraversal();
	printf("层序遍历："); avltree.LevelOrderTraversal();
	
	root = avltree.GetRoot();
	avltree.DeleteNode(9);   // RR 、 LL
	/* The AVL Tree after the deletion of 10
					5
				 /      \
			   0          8
			 /  \       /   \
			-1   1     6     11
		          \     \   /  \
		           2     7  9  12
	*/
	printf("层序遍历："); avltree.LevelOrderTraversal();


	cout << "\n......................\n" << endl;

	/* The constructed AVL Tree would be
				9
			 /     \
		   4        11
		 /  \       /  \
		0     6    10   12
	   / \   /  \         \
	  -1  1  5   7         13
		          \
			       8
	*/
	int arr2[] = { 9, 4, 10, 0, 6, 11, 12, -1, 1, 5, 7, 13, 8 };
	size = sizeof(arr2) / sizeof(arr2[0]);
	AVLTree<int> avltree2(arr2, size);
	root = avltree2.GetRoot();
	printf("前序遍历："); avltree2.PreOrderTraversal();
	printf("层序遍历："); avltree2.LevelOrderTraversal();

	avltree2.DeleteNode(13);   // LR 
	/* The AVL Tree after the deletion of 10
					6
				 /      \
			   4          9
			 /  \       /   \
		   0     5     7     11
		  /  \	        \    /  \
		 -1  1	         8  10  12
	*/
	printf("层序遍历："); avltree2.LevelOrderTraversal();


	return 0;
}

本节的一部分图片来自：(2条消息) 平衡二叉树--AVL 的原理及实现_阿尔兹的博客-CSDN博客

七、构建最小堆树

????????堆树包括最大堆树（最小堆树），是完全二叉树且父节点不小于（不大于）子节点，且左右子树也都是最大堆树（最小堆树）。最小堆树、最大堆树，又称小顶堆、大顶堆。

7.1 整个最小堆树的构建过程：

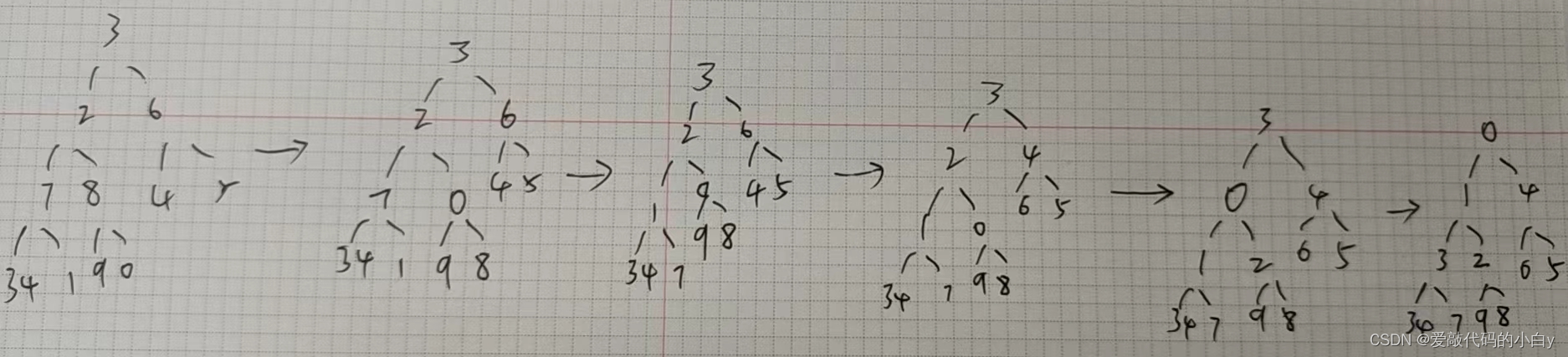
?7.2 最小堆树删除堆顶元素0的过程：

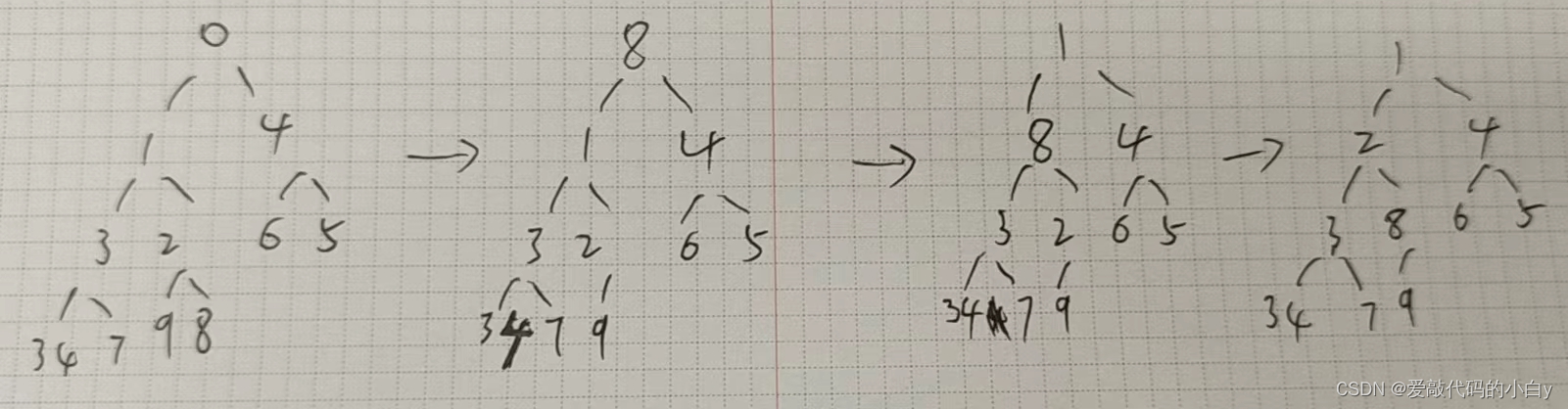
?7.3 最小堆树插入元素-1的过程：

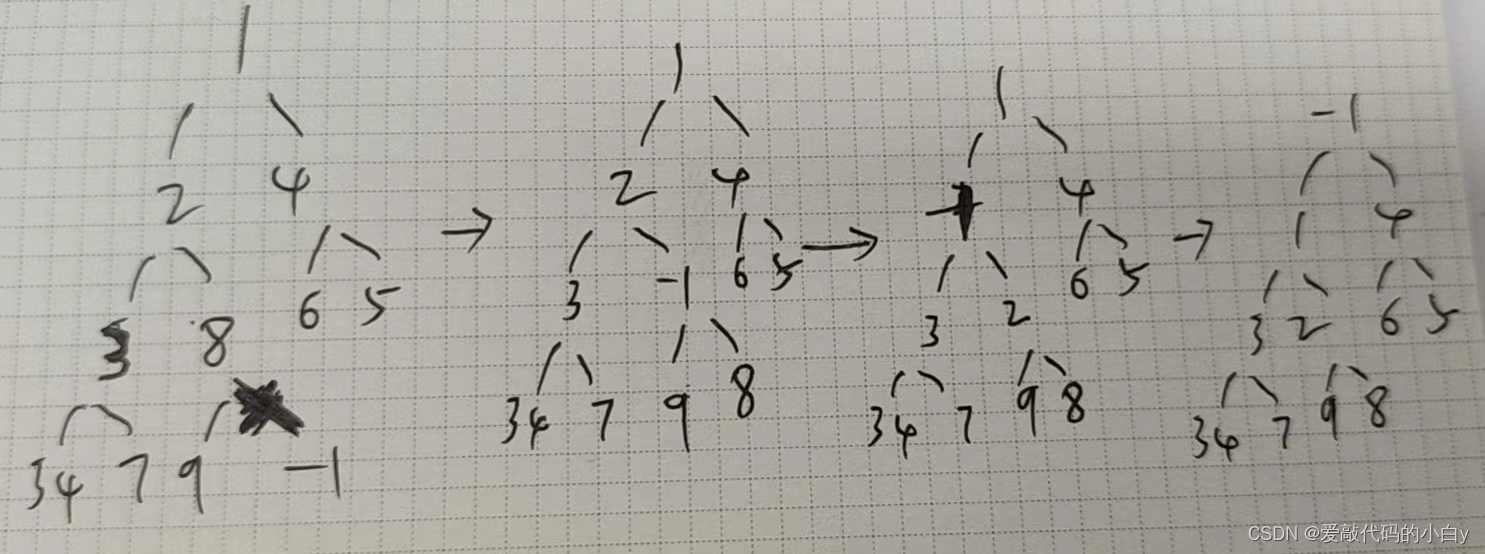
?MinHeap.hpp

#pragma once
#include <iostream>
using namespace std;
#define DEFAULT_SIZE 10    

// 最小堆树：实际上是满足父节点值不大于子节点的值，且左右子树均是最小堆树的完全二叉树
template <class T>
class MinHeap 
{
public:
	MinHeap(int size = DEFAULT_SIZE);  // 用0来初始化堆数组heap_array_
	MinHeap(T* arr, int arr_size);     // 用数组arr来初始化堆数组heap_array_，并调整顺序使heap_array_堆数组满足最小堆树的要求，即父节点值不大于子节点的值，且左右子树均满足
	~MinHeap() { delete[] heap_array_; }

	bool IsEmpty() const { return m_size == 0 ? true : false; }
	bool IsFull() const { return m_size == m_capacity ? true : false; }
	int GetLevel();  

	bool Insert(const T& item);
	bool RemoveMin(T& value);

	ostream& showMinHeapTree(ostream& out, int size, T* heap_arr_);
	template<class T>
	friend ostream& operator<<(ostream& out, const MinHeap<T>& minHeap);
private:
	T* heap_array_;
	int m_size;
	int m_capacity;

	void shiftDown(int start, int end);
	void shiftUp(int start);
};

template<class T>
int MinHeap<T>::GetLevel()
{
	int level = 0;
	while ((pow(2, level) - 1) < this->m_size)
	{
		level++;
	}
	return level;
}

template<class T>
ostream& MinHeap<T>::showMinHeapTree(ostream& out, int size, T* heap_arr_)
{
	// 按照行优先，且从左到右的顺序，打印输出二叉树的节点数据，等价于层序遍历
	for (int i = 0; i < size; i++)
	{
		out << heap_arr_[i];
		if (i != size - 1)
		{
			out << ",";
		}
	}
	out << endl;
	return out;
}
template<class T>
ostream& operator<<(ostream& out, const MinHeap<T>& heap)
{	
	heap.showMinHeapTree(out, heap.m_size, heap.heap_array_);
	return out;
}

template <class T>
MinHeap<T>::MinHeap(int size) 
{
	m_capacity = (size > DEFAULT_SIZE) ? size : DEFAULT_SIZE;
	heap_array_ = new T[m_capacity];
	for (int i = 0; i < m_capacity; i++)
	{
		heap_array_[i] = 0;
	}
	m_size = 0;
}

template <class T>
MinHeap<T>::MinHeap(T* arr, int arr_size) 
{
	m_capacity = (arr_size > DEFAULT_SIZE) ? arr_size : DEFAULT_SIZE;
	heap_array_ = new T[m_capacity];

	// 初始化heap_array_时，先将arr拷贝过来，再逐个调整
	for (int i = 0; i < arr_size; i++) 
	{
		heap_array_[i] = arr[i];
	}
	m_size = arr_size;

	// 调整顺序使heap_array_堆数组满足最小堆树的要求，即父节点值不大于子节点的值，且左右子树均是最小堆树
	int current_index_ = (int)(m_size - 2) / 2;   // 此时，current_index_是最小堆树中，最后一个元素的父节点在heap_array_中的索引
	// 从下到上，逐个调整子节点与父节点对应键值的大小关系，直到满足最小堆树特性（从最后一个元素对应的父节点的位置开始调整，直到调整到根节点）
	while (current_index_ >= 0) 
	{
		shiftDown(current_index_, m_size - 1);
		current_index_--;
	}
}

template <class T>
void MinHeap<T>::shiftDown(int start, int end) 
{
	int cur = start;
	int left_child = 2 * cur + 1; int min_child = left_child;
	int right_child = left_child + 1;

	T cur_value = heap_array_[cur];

	while (left_child <= end) 
	{
		// 找到父节点cur对应的最小的子节点
		if (heap_array_[left_child] > heap_array_[right_child]) 
		{
			min_child = right_child;
		}
		// 如果父节点cur对应的键值小于最小的子节点对应的键值，表明不用再调整了，即跳出while循环
		if (cur_value <= heap_array_[min_child]) 
		{
			break;
		}
		else 
		{
			// 找到了比父节点小的子节点并用子节点的值代替父节点的值
			heap_array_[cur] = heap_array_[min_child];

			// 继续寻找其最小的子节点作为父节点时，最小的子节点，从而来替换其的父节点
			cur = min_child;
			left_child = 2 * min_child + 1; min_child = left_child;
			right_child = left_child + 1;	
		}
	}
	// 将待向下调整的节点的数据cur_value，赋给最终找到的能满足最小堆树特性的节点位置cur
	heap_array_[cur] = cur_value;
}
// 最小堆堆顶节点删除思想：将堆树的最后的节点提到根结点，并删除将heap_array_堆数组的大小减一，然后将堆顶的元素不断向下调整，直到满足最小堆树的特性
template <class T>
bool MinHeap<T>::RemoveMin(T& x)
{
	if (!m_size)
	{
		cout << "Heap Empty." << endl;
		return false;
	}

	// 将heap_array_中最后一个元素，放在根节点；并m_size减一；表示删除了一个堆顶的元素并用最后一个元素代替
	x = heap_array_[0];
	heap_array_[0] = heap_array_[m_size - 1];  
	m_size--;

	// 重新向下调整，使完全二叉树满足最小堆树的特性
	shiftDown(0, m_size - 1);
	return true;
}


// 最小堆的插入节点的思想：就是先在堆的最后添加一个节点，然后沿着最小堆树不断向上调整，直到满足最小堆树的特性
template <class T>
void MinHeap<T>::shiftUp(int start) 
{
	int j = start; int father = (j - 1) / 2;
	T temp = heap_array_[j];

	while (j > 0) 
	{
		// 只需要不断比对，父节点father与待向上调整的数据temp对应键值的大小关系
		if (heap_array_[father] <= temp) // 满足父节点不大于temp，则表明调整完成，退出while
		{
			break;
		}
		else 
		{
			// 当父节点大于temp时，则需要将父节点的值赋给对应的子节点j
			heap_array_[j] = heap_array_[father];
			// 重新寻找father对应的父节点是否不大于temp
			j = father;
			father = (j - 1) / 2;
		}
	}
	// 最后将待向上调整的数据，插入到最终找到其满足最小堆树特性的对应的位置j
	heap_array_[j] = temp;
}
template <class T>
bool MinHeap<T>::Insert(const T& item) 
{
	if (m_size == m_capacity) 
	{
		cout << "Heap Full." << endl;
		return false;
	}

	// 插入一个元素item
	heap_array_[m_size] = item;

	// 将m_size位置的刚插入的元素item，向上调整，直到满足最小堆树的特性
	shiftUp(m_size);

	m_size++;
	return true;
}

?main.cpp

#include "MinHeap.hpp"

int main() 
{
	int arr[] = { 3,2,6,7,8,4,5,34,1,9,0 };

	MinHeap<int> heap(arr, sizeof(arr) / sizeof(arr[0]));
	cout << heap;

	// 插入元素后，此时堆树已经满了
	heap.Insert(99);
	
	// 删除最小堆树中堆顶的元素，即最小值，然后插入一个元素-1
	int item;
	heap.RemoveMin(item);
	cout << heap;
	heap.Insert(-1);
	cout << heap;

	cout << "is full:" << heap.IsFull() << endl;        // 1表示true；0表示false
	cout << "is empty:" << heap.IsEmpty() << endl;
	cout << endl;

	// 展示不断删除最小堆树中堆顶的元素后，最小堆树的变化（通过层序遍历展示）
	cout << heap;
	while (!heap.IsEmpty())
	{
		heap.RemoveMin(item);
		cout << heap;
	}
	
	return 0;
}

八、构建霍夫曼树?

霍夫曼树的经常用于处理数据压缩，可以根据数据出现的频率来构建二叉树；

例如，存在五个数据的出现频率为0.09、0.21、0.13、0.19、0.39，同时为了确保霍夫曼树的唯一性，需要使父节点的左子节点的频率小于右子节点。

具体步骤如下：

1）取出最小的两个数据0.09、0.13合成一个父节点是0.09+0.13=0.22的子树；

2）将上一步得到的父节点0.22与剩余的数据重新组成四个数据，并从中再找出两个最小的数据；同理构成子树，并将子树的父节点与剩余的数据重新组成三个数据，直到数据全部在树中；

最终，如果规定霍夫曼树：左分支为1、右分支为0，则0.09、0.21、0.13、0.19、0.39这五个数据的一种最优压缩对应的是011、10、010、11、00。

HuffmanTree.hpp?

#include <iostream>
#include "MinHeap.hpp"
using namespace std;

template <class T>
class HuffmanNode 
{
public:
	HuffmanNode() : left(NULL), right(NULL), parent(NULL) {}
	HuffmanNode(T val, HuffmanNode<T>* left = NULL, HuffmanNode<T>* right = NULL, HuffmanNode<T>* parent = NULL) :
		data(val), left(left), right(right), parent(parent) {}

	// 重载的<=、>运算符，用于最小堆中的构建最小堆树时不断调整过程中的HuffmanNode<T>类型数据的比较，即是 if(heap_array_[left_child] > heap_array_[right_child]) 和 if(cur_value <= heap_array_[min_child]) 条件的判断
	bool operator<=(const HuffmanNode<T>& R) { return this->data <= R.data; }
	bool operator>(const HuffmanNode<T>& R) { return this->data > R.data; }
public:
	T data;
	HuffmanNode<T>* left;
	HuffmanNode<T>* right;
	HuffmanNode<T>* parent;
};

template <class T>
class HuffmanTree 
{
public:
	HuffmanTree(T* arr, int size);
	~HuffmanTree() { this->clear(this->root); }
	HuffmanNode<T>* GetRoot() { return this->root; }

	template <class T>
	friend ostream& operator<<(ostream& out, const HuffmanTree<T>& huffmantree);
private:
	HuffmanNode<T>* root;
	void clear(HuffmanNode<T>* sub_tree_rootNode);
	// 用节点node1和node2构成新的子树，且子树的根节点时parent（其节点的键值是node1+node2）
	void mergeTree(HuffmanNode<T>* node1, HuffmanNode<T>* node2, HuffmanNode<T>*& parent);
	void showTree(HuffmanNode<T> * sub_tree_rootNode, ostream& out);
};

template <class T>
HuffmanTree<T>::HuffmanTree(T* arr, int arr_size) 
{
	// 创建MinHeap堆树的类对象heap
	MinHeap<HuffmanNode<T>> heap;

	for (int i = 0; i < arr_size; i++) 
	{
		HuffmanNode<T>* tempNode = new HuffmanNode<T>(arr[i], NULL, NULL, NULL);
		tempNode->parent = tempNode;   // 初始化时，每个节点的父节点都是自己
		heap.Insert(*tempNode);        // 将HuffmanNode<T>的对象，插入到最小堆树中
	}

	HuffmanNode<T> *parent = NULL;
	HuffmanNode<T> *first = NULL;
	HuffmanNode<T> *second = NULL;
	for (int i = 0; i < arr_size - 1; i++)    
	{
		HuffmanNode<T> temp;
		heap.RemoveMin(temp); first = temp.parent;
		heap.RemoveMin(temp); second = temp.parent;
		mergeTree(first, second, parent);   // 每次从HuffmanNode<T>中拿出的最小的两个，用来构建子树后合并出一个父节点，重新放入堆中；并继续循环，直到heap为空
		heap.Insert(*parent);
	}

	this->root = parent;   // 最小堆中，最后剩余的一个元素，即是该霍夫曼树的根节点
}

template <class T>
void HuffmanTree<T>::mergeTree(HuffmanNode<T>* node1, HuffmanNode<T>* node2, HuffmanNode<T>*& parentNode)
{
	parentNode = new HuffmanNode<T>(node1->data + node2->data, node1, node2, NULL);
	parentNode->parent = parentNode;
	node1->parent = node2->parent = parentNode;
}

template <class T>
void HuffmanTree<T>::clear(HuffmanNode<T>* sub_tree_rootNode)
{
	if (sub_tree_rootNode == NULL)
	{
		sub_tree_rootNode = nullptr;
		return;
	}

	clear(sub_tree_rootNode->left);
	clear(sub_tree_rootNode->right);

	delete sub_tree_rootNode;
	sub_tree_rootNode = nullptr;
}

template <class T>
void HuffmanTree<T>::showTree(HuffmanNode<T>* sub_tree_rootNode, ostream& out) 
{
	if (sub_tree_rootNode == NULL) { return; }       // 递归结束的条件

	cout << '('; cout << sub_tree_rootNode->data; cout << ',';
	if (sub_tree_rootNode->left != NULL) { showTree(sub_tree_rootNode->left, out); }
	if (sub_tree_rootNode->right != NULL) { showTree(sub_tree_rootNode->right, out); }
	cout << ')';
}
template <class T>
ostream& operator<<(ostream& out, const HuffmanTree<T>& huffmantree)
{
	huffmantree.showTree(huffmantree.GetRoot(), out);
	return out;
}

main.cpp

#include "MinHeap.hpp"
#include "HuffmanTree.hpp"

int main() 
{
	float arr[] = { 0.09,0.13,0.19,0.21,0.39 };
	int n = sizeof(arr) / sizeof(arr[0]);

	HuffmanTree<float> huffmantree(arr, n);

	cout << huffmantree << endl;

	return 0;
}

?九、红黑树RBTree

? ? ? ? 基于BST存在的问题，一种新的树平衡二叉查找树(Balanced BST)AVL产生了。平衡树在插入和删除的时候，会通过旋转操作将高度保持在logN。其中两款具有代表性的平衡树分别为AVL树和红黑树。AVL树由于实现比较复杂，且插入和删除性能差，在实际环境下的应用不如红黑树。

????????红黑树的5个性质：

• 每个结点要么是红的，要么是黑的；
• 根结点是黑的；
• 每个叶节点，即空节点（NIL /?NULL）是黑的；
• 如果红节点的俩个儿子都是黑的，即红黑树的所有路径中不能出现连续的红节点；
• 对每个节点，从该节点到其子孙节点的所有路径上包含相同数目的黑节点；

????????红黑树的节点结构：颜色（red/black）、<key,value>、父结点（根结点的父结点为null）、左子结点、右子结点。

9.1 插入操作

????????首先红黑树要找到真正插入节点的位置，且设定插入节点的颜色为红色（如果插入的是黑色节点，必然会改变了红黑树的黑高度，进而违背红黑树的特性），之后再做旋转、变色等操作。

????????如下插入红色结点后，特别容易出现连续的两个红节点的情况，故需要进行插入后的修复操作。修复时，存在的几种情况：

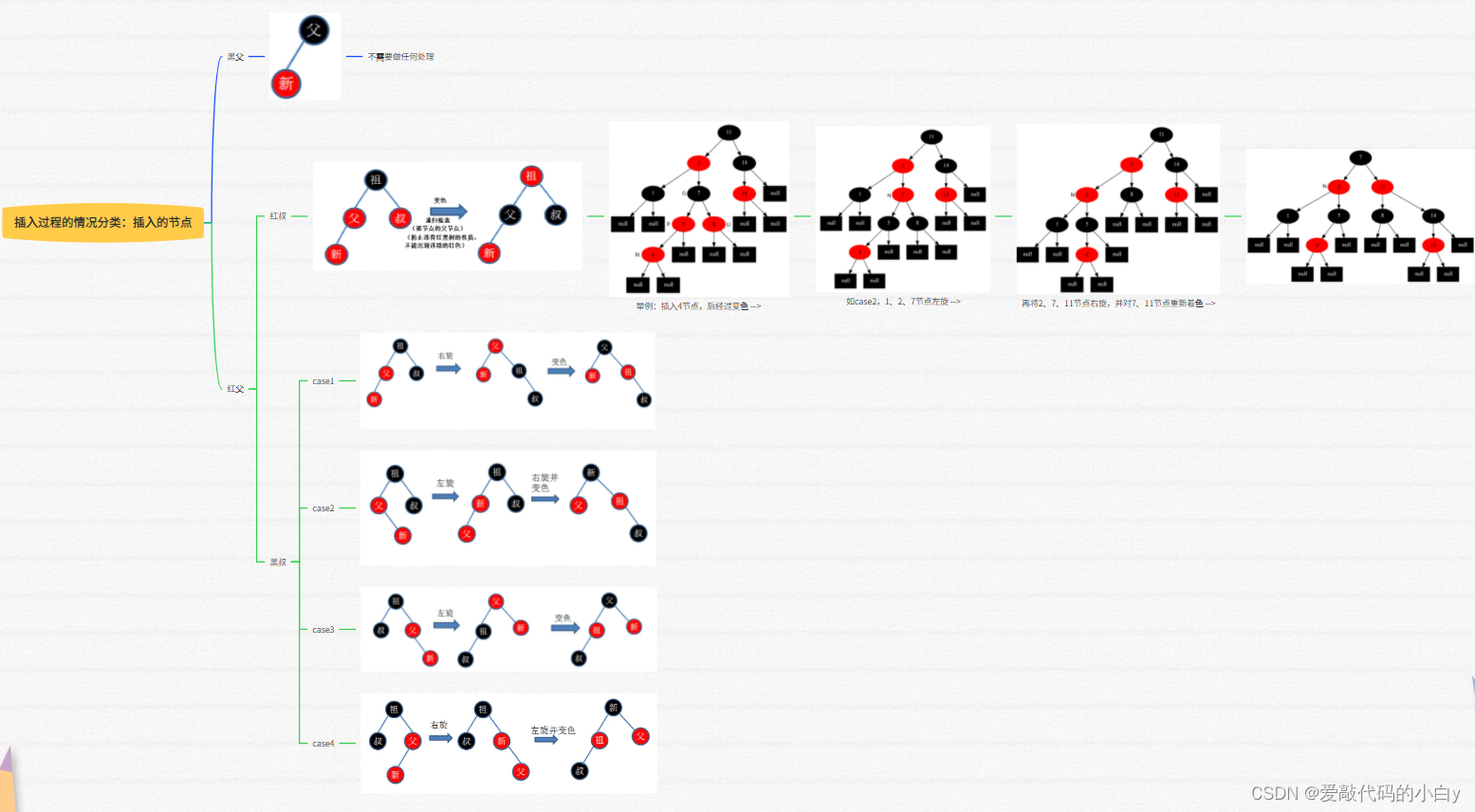
1.?黑父

如下图所示，这种情况不会破坏红黑树的特性，即不需要任何处理。

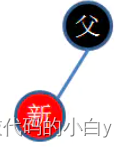
2.?红父

当其父亲为红色时，又会存在以下的情况：

• 红叔

????????如下图所示，只需要将父、叔的颜色改为黑色，祖改为红色。但由于祖父结点的父结点有可能为红色，从而违反红黑树性质，故此时必须将祖父结点作为新的判定点继续向上进行平衡操作。

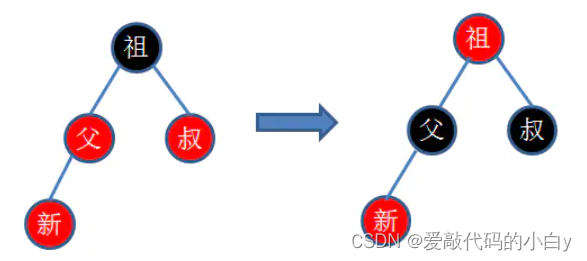
• 黑叔

????????黑叔的情况有如下几种，这几种情况是不能够通过修改颜色来达到平衡的效果，故需要额外通过旋转操作来实现。红黑树有两种旋转操作，左旋和右旋。注意：下图可能含有黑哨兵节点。

• Case 1：[先右旋，再改变颜色（根节点必须为黑色，其两个子节点为红色，叔节点不用改变）]，如下图所示。

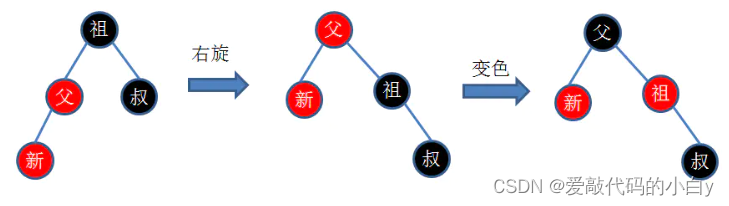
• Case 2：[先左旋变成Case1中的情况，再右旋，最后改变颜色（根节点必须为黑色，其两个子节点为红色，叔节点不用改变）]，如下图所示。

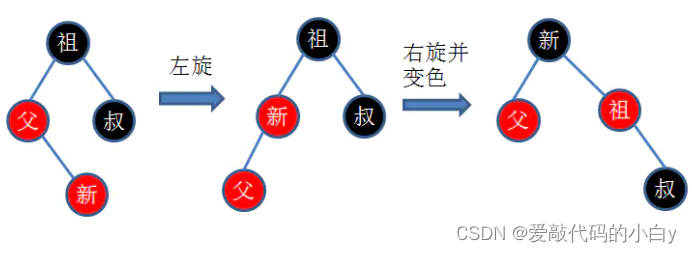
• Case 3：[先左旋，最后改变颜色（根节点必须为黑色，其两个子节点为红色，叔节点不用改变）]，如下图所示。

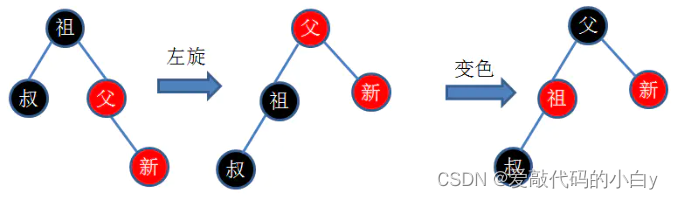
• Case 4：[先右旋变成Case 3的情况，再左旋，最后改变颜色（根节点必须为黑色，其两个子节点为红色，叔节点不用改变）]，如下图所示。

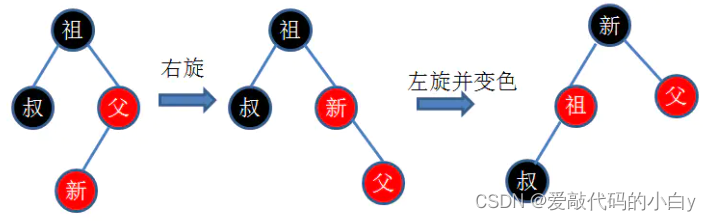
?9.2 删除操作

????????与红黑树插入操作类似，红黑树的删除操作也是通过?重新着色?和?旋转，来保证每一次删除操作后依旧满足红黑树的5条性质。而删除操作，最容易造成子树黑高度的变化（删除黑色结点可能导致根结点到叶结点黑色结点的数目减少，即黑高降低）。

? ? ? ? 删除操作相比于插入操作情况更加复杂：首先要找到真正的删除点，当被删除结点n存在左右孩子时，真正的删除点应该是n的中序前驱/后继节点（这里以后继节点为例）（删除操作中真正被删除的，必定是只有一个红色孩子或没有孩子的节点；如果真正的删除点是一个红色节点，那么它必定是一个叶子节点）。（注意，这里不考虑含有黑哨兵节点）

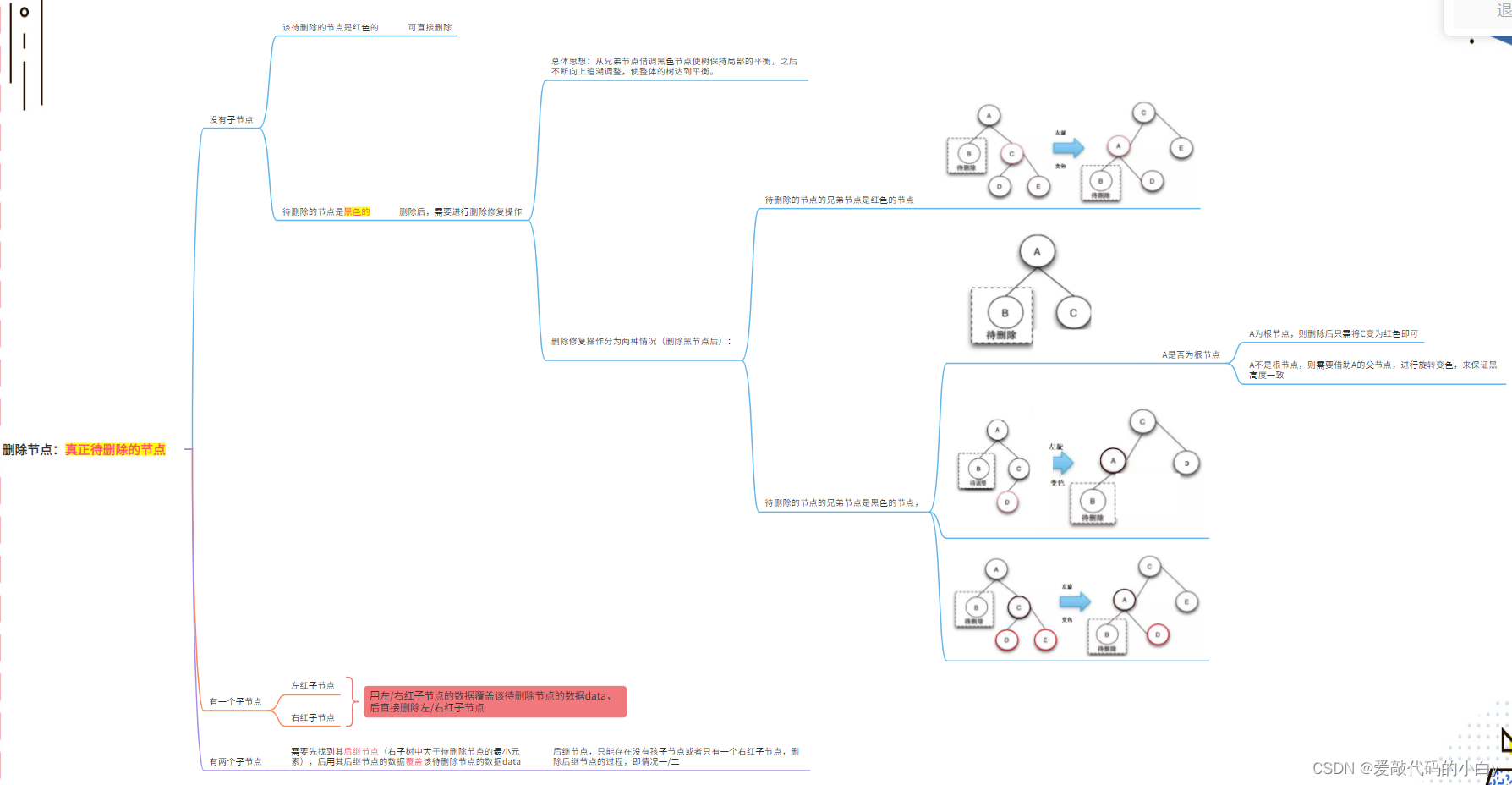
?结语：不论是红黑树的插入还是删除的过程中，涉及的树的旋转、变色，都只为了保持和修复红黑树的5个性质。

十、B/B+树

10.1 B树的插入和删除操作：

给定一组关键字{20，30，50，52，60，68，70}，创建一棵m=3阶B树。B树除根节点外，每个节点的key个数满足：[[m/2] - 1, m - 1]。

10.1.1 B树的插入操作

????????分裂的方法：取这个关键字数组中的中间关键字[n/2]（向上取整）作为新的结点，然后其他关键字形成两个结点作为新结点的左右孩子。

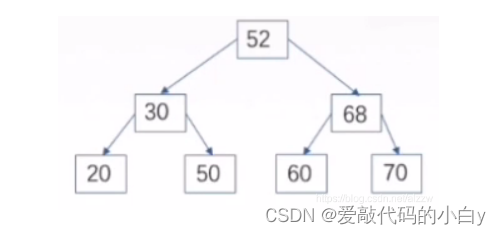
?10.1.2 B树的删除操作

????????B树中的删除操作是根据key删除记录的，如果B树中的记录中不存对应key的记录，则删除失败。B树中的删除，将涉及结点的“合并”问题，具体步骤如下：

10.2 B+树的插入和删除操作：?

给定一组关键字{5，6，7，8，9，10，15，16，17，18，19，21，22}，给出创建一棵m=5阶B+树的过程。B+树除根节点外，每个节点的key个数满足：[[m/2] - 1, m - 1]

10.2.1 B+树的插入操作：

1）若为空树，创建一个叶子结点，然后将记录插入其中，此时这个叶子结点也是根结点，插入操作结束。

2）针对叶子结点：根据key值找到叶子结点，向这个叶子结点插入记录。插入后，

• 若当前结点key的个数 <= m-1，则插入结束。
• 若当前结点key的个数 >?m-1，则将这个叶子结点分裂成左右两个叶子结点，左叶子结点包含前m/2个记录，右结点包含剩下的记录，并将第m/2+1个记录的key进位到父结点中，进位到父结点的key左孩子指针向左结点，右孩子指针向右结点。将当前结点的指针指向父结点，然后执行第3步。

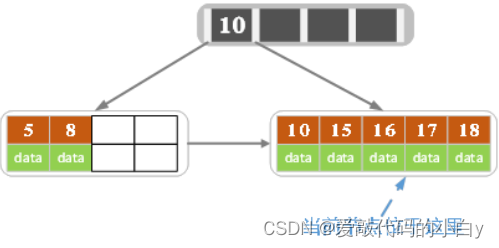
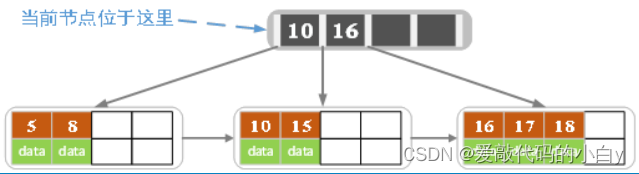
3）针对索引结点：

• 若当前结点key的个数 <= m-1，则插入结束。
• 若当前结点key的个数 > m-1，将这个索引类型结点分裂成两个索引结点，左索引结点包含前[m/2]-1个key，右结点包含剩余的key，将第m/2个key进位到父结点中，进位到父结点的key左孩子指向左结点, 进位到父结点的key右孩子指向右结点。将当前结点的指针指向父结点，然后重复步骤3），直到回溯到根节点。

?

最终，不断插入后形成的B+树，如下图。?

10.2.2 B+树的删除操作：

如果叶子结点中没有相应的key，则删除失败。否则执行下面的步骤：

1）删除叶子结点中对应的key。删除后若结点的key的个数 >= [m/2] - 1，删除操作结束。否则执行下列步骤：

• 若兄弟结点key有富余（大于[m/2]?– 1），则向兄弟结点借一个记录，同时用借到的key替换父结（指当前结点和兄弟结点共同的父结点）点中的key，删除结束。
• 若兄弟结点中没有富余的key，则当前结点和兄弟结点合并成一个新的叶子结点，并删除父结点中的key（父结点中的这个key两边的孩子指针就变成了一个指针，正好指向这个新的叶子结点），将当前结点指向父结点（必为索引结点）。

接下来的操作，主要是调整索引节点，使其满足“B+树除根节点外，每个节点的key个数满足：[[m/2] - 1, m - 1]”的性质。

2）若索引结点的key的个数 >= [m/2] - 1，则删除操作结束。否则执行下列步骤：

• 若兄弟结点有富余，父结点key下移，兄弟结点key上移，删除结束。
• 若兄弟节点没有富余，当前结点和兄弟结点及父结点下移key合并成一个新的结点。将当前结点指向父结点，操作过程如下图。之后不断重复步骤2），直到回溯到根节点结束。

注意，通过B+树的删除操作后，索引结点中存在的key，不一定在叶子结点中存在对应的记录。