贪心的本质是选择每一阶段的局部最优,从而达到全局最优。
贪心算法并没有固定的套路。因而需要进一步巩固,多做做多有感觉才行。
这次巩固题目来源:代码随想录
1.贪心简单题
(1)分发饼干,已做过。
(2)1005.K次取反后最大化的数组和

?其实模拟就能做(每次改变最小的其实也是一种贪心)
class Solution {
public:
int largestSumAfterKNegations(vector<int>& nums, int k) {
int max = 0;
for (int i = 0; i < nums.size(); ++i) {
max += nums[i];
}
while (k--) {
int min = nums[0];
int dex = 0;
for (int i = 0; i < nums.size(); ++i) {
if (min > nums[i]) {
min = nums[i];
dex = i;
}
}
max -= nums[dex];
nums[dex] = -nums[dex];
max += nums[dex];
}
return max;
}
贪心也行:
/*第一步:将数组按照绝对值大小从大到小排序,注意要按照绝对值的大小
第二步:从前向后遍历,遇到负数将其变为正数,同时K--
第三步:如果K还大于0,那么反复转变数值最小的元素,将K用完
第四步:求和*/
static bool cmp(int a, int b) {
return abs(a) > abs(b);
}
public:
int largestSumAfterKNegations(vector<int>& A, int K) {
sort(A.begin(), A.end(), cmp); // 第一步
for (int i = 0; i < A.size(); i++) { // 第二步
if (A[i] < 0 && K > 0) {
A[i] *= -1;
K--;
}
}
if (K % 2 == 1) A[A.size() - 1] *= -1; // 第三步
int result = 0;
for (int a : A) result += a; // 第四步
return result;
}(3)860.柠檬水找零


- 情况一:账单是5,直接收下。
- 情况二:账单是10,消耗一个5,增加一个10
- 情况三:账单是20,优先消耗一个10和一个5,如果不够,再消耗三个5
class Solution {
public:
bool lemonadeChange(vector<int>& bills) {
vector<int> cur(3,0);
for (int i = 0; i < bills.size(); ++i) {
if (bills[i] == 5) {
cur[0] += 1;
continue;
}
if (bills[i] == 10) {
cur[1] += 1;
if (cur[0] > 0) {
--cur[0];
}
else {
return false;
}
}
if (bills[i] == 20) {
cur[2] += 1;
if (cur[0] > 0 && cur[1] > 0) {
--cur[0];
--cur[1];
}
else if (cur[0] >= 3) {
cur[0] -= 3;
}
else {
return false;
}
}
}
return true;
}
};2.贪心中等题
贪心中等题,靠常识可能就有点想不出来了。开始初现贪心算法的难度与巧妙之处。
(1)738.单调递增的数字
这个说白了是个数学问题,怎么能最小呢?
首先先把每一位存到数组里面,然后从后往前遍历:
? ? ?* 思路:
? ? ?* ?从右向左扫描数字,若发现当前数字比其左边一位(较高位)小,
? ? ?* ?则把其左边一位数字减1,并将该位及其右边的所有位改成9?仔细想想,这很正确
class Solution {
public:
void turnNine(vector<int>& num,int left) {
for (int i = left; i < num.size(); ++i) {
num[i] = 9;
}
}
int monotoneIncreasingDigits(int n) {
int len = 0;
int temp = n;
while (temp) {
++len;
temp = temp / 10;
}
temp = n;
vector<int> num(len);
int i = len - 1;
while (temp) {
int tail = temp % 10;
temp /= 10;
num[i--] = tail;
}
/**
* 思路:
* 从右向左扫描数字,若发现当前数字比其左边一位(较高位)小,
* 则把其左边一位数字减1,并将该位及其右边的所有位改成9
*/
for (int i = len - 1; i > 0; --i) {
if (num[i - 1] > num[i]) {
num[i - 1] -= 1;
turnNine(num, i);
}
}
int rs = 0;
for (int i = 0; i < len; ++i) {
rs = rs * 10 + num[i];
}
return rs;
}
};(2)376. 摆动序列
这还真的挺难,不会做

法一:贪心
//贪心,转化为上坡下坡,有几个坡。最后不忘加一就行(这里事先就加一了)
//保持区间波动,只需要把单调区间上的元素移除就可以了。?
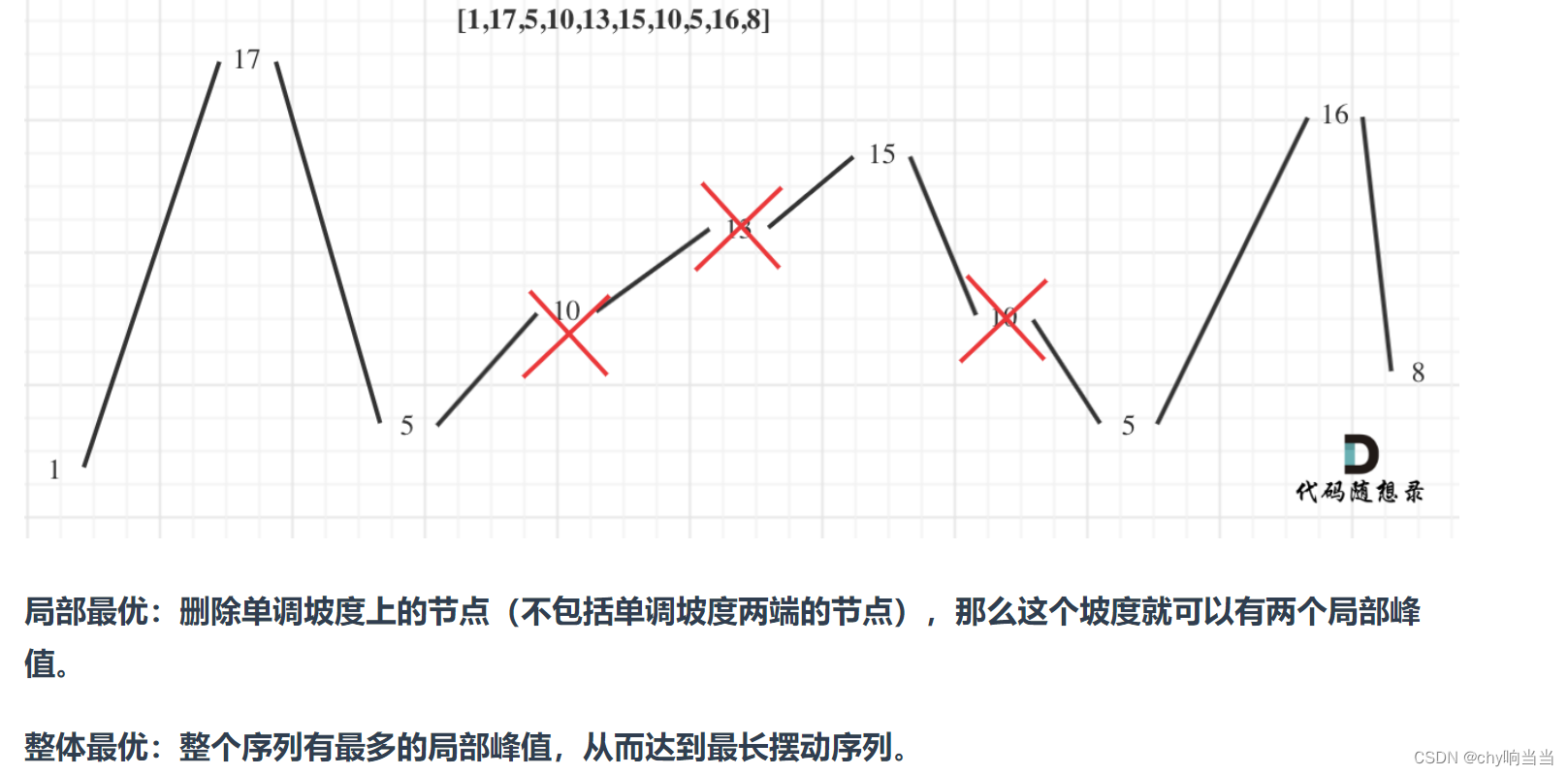
?实际操作上,其实连删除的操作都不用做,因为题目要求的是最长摆动子序列的长度,所以只需要统计数组的峰值数量就可以了(相当于是删除单一坡度上的节点,然后统计长度)
这就是贪心所贪的地方,让峰值尽可能的保持峰值,然后删除单一坡度上的节点。
于是这就转化为了求有几个坡( 包括上坡下坡)的问题
class Solution1{
public:
//注意不能为0
int wiggleMaxLength(vector<int>& nums) {
if (nums.size() <= 1) return nums.size();
int curDiff = 0; // 当前一对差值
int preDiff = 0; // 前一对差值
int result = 1; // 记录峰值个数,序列默认序列最右边有一个峰值
for (int i = 0; i < nums.size() - 1; i++) {
curDiff = nums[i + 1] - nums[i];
// 出现峰值
//cur不能为0,prediff=0仅仅在第一次判断时用,我们假设0号元素(也就是第一个元素)的prediff=0
if ((curDiff > 0 && preDiff <= 0) //当前上坡,前一个下坡
|| (preDiff >= 0 && curDiff < 0)) {//前一个上坡,当前下坡
result++;
preDiff = curDiff;
}
}
return result;
}
};法二 dp
设dp状态dp[i][0],表示考虑前i个数,第i个数作为山峰的摆动子序列的最长长度
设dp状态dp[i][1],表示考虑前i个数,第i个数作为山谷的摆动子序列的最长长度
dp[i][0] = max(dp[i][0], dp[j][1] + 1),其中0 < j < i且nums[j] < nums[i],
表示将nums[i]接到前面某个山谷后面,作为山峰。
dp[i][1] = max(dp[i][1], dp[j][0] + 1),其中0 < j < i且nums[j] > nums[i],
表示将nums[i]接到前面某个山峰后面,作为山谷
class Solution {
public:
int dp[1005][2];
int wiggleMaxLength(vector<int>& nums) {
memset(dp, 0, sizeof dp);
dp[0][0] = dp[0][1] = 1;
for (int i = 1; i < nums.size(); ++i)
{
dp[i][0] = dp[i][1] = 1;
for (int j = 0; j < i; ++j)
{
if (nums[j] > nums[i]) dp[i][1] = max(dp[i][1], dp[j][0] + 1);
}
for (int j = 0; j < i; ++j)
{
if (nums[j] < nums[i]) dp[i][0] = max(dp[i][0], dp[j][1] + 1);
}
}
return max(dp[nums.size() - 1][0], dp[nums.size() - 1][1]);
}
};3.贪心解决股票问题
(1)122.买卖股票的最佳时机II
做过了,思路就是每天都可以卖出然后买进,只要比昨天高就卖然后再买
[7, 1, 5, 6]? ?——》??(5-1)+ (6-5)= 5
(2)714. 买卖股票的最佳时机含手续费
这个就不会了。好好审题。

法一贪心
本题有了手续费,就要关系什么时候买卖了,因为计算所获得利润,需要考虑买卖利润可能不足以手续费的情况。
如果使用贪心策略,就是最低值买,最高值(如果算上手续费还盈利)就卖
无非就是要找到两个点,买入日期,和卖出日期
所以我们在做收获利润操作的时候其实有三种情况:
?这三个情况要深刻体会,尤其是第一种,如何用代码实现,并且和第二种连接。
//妙,很难,多思考
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int result = 0;
int minPrice = prices[0]; // 记录最低价格
for (int i = 1; i < prices.size(); i++) {
// 情况二:相当于买入
if (prices[i] < minPrice) minPrice = prices[i];
// 情况三:保持原有状态(因为此时买则不便宜,卖则亏本)
if (prices[i] >= minPrice && prices[i] <= minPrice + fee) {
continue;
}
// 计算利润,可能有多次计算利润,最后一次计算利润才是真正意义的卖出
if (prices[i] > minPrice + fee) {
result += prices[i] - minPrice - fee;
minPrice = prices[i] - fee; // 情况一,这一步很关键
}
}
return result;
}
};
- 时间复杂度:O(n)
- 空间复杂度:O(1)
从代码中可以看出对情况一的操作,因为如果还在收获利润的区间里,表示并不是真正的卖出,而计算利润每次都要减去手续费,所以要让minPrice = prices[i] - fee;,这样在明天收获利润的时候,才不会多减一次手续费!
这里有个更好理解的:
class Solution {
public int maxProfit(int[] prices, int fee) {
if (prices.length == 1) return 0; // 长度为1,没有交易空间;
int base = prices[0] + fee; // 本身带交易费的买入,后面高于这个部分的,都是利润;
int profit = 0;
for (int i = 1; i < prices.length; ++i) {
if (prices[i] > base) { // 高于的,都是利润;
profit += prices[i] - base;
base = prices[i]; // 一直往上走;
}
else if (prices[i] + fee < base) { // 一旦遇到下降,说明利润达到顶点了,转为下滑;
// 不断试探,最低点(买入点)在哪里;但是只要遇到高点,if语句就会加入利润
base = prices[i] + fee;
}
}
return profit;
}
}法二dp
dp1[i]表示第i天手上有股票,dp2[i]表示第i天手上没有股票,递归方程:
dp1[i] = max(dp1[i-1], dp2[i-1] - prices[i]) (第二项表示在第i天买入股票)
dp2[i] = max(dp2[i-1], dp1[i-1] + prices[i] - fee) (第二项表示在第i天将股票卖出,需扣除手续费)
class Solution2 {
public:
int maxProfit(vector<int>& prices, int fee) {
vector<int>dp1(prices.size(), 0);
vector<int>dp2(prices.size(), 0);
if (prices.size() < 2) {
return 0;
}
dp1[0] -= prices[0];
for (int i = 1; i < prices.size(); ++i) {
dp1[i] = max( dp1[i - 1],dp2[i - 1] - prices[i] );
dp2[i] = max(dp2[i - 1], dp1[i - 1] - fee+ prices[i]);
}
//最后一天后肯定都卖了
return dp2[prices.size() - 1];
}
};
4.两个维度权衡问题? ?
分发糖果和根据身高重建队列
遇到两个维度权衡的时候,一定要先确定一个维度,再确定另一个维度。
如果两个维度一起考虑一定会顾此失彼。
比如重建队列:
如果按照k来从小到大排序,排完之后,会发现k的排列并不符合条件,身高也不符合条件,两个维度哪一个都没确定下来。
那么按照身高h来排序呢,身高一定是从大到小排(身高相同的话则k小的站前面),让高个子在前面。
此时我们可以确定一个维度了,就是身高,前面的节点一定都比本节点高!
5.区间问题
(1)

?(2)55. 跳跃游戏

//跳跃覆盖范围究竟可不可以覆盖到终点
//贪心算法局部最优解:每次取最大跳跃步数(取最大覆盖范围),
//整体最优解:最后得到整体最大覆盖范围,看是否能到终点。
class Solution {
public:
bool canJump(vector<int>& nums) {
int cur = 0;
if (nums.size() <= 1) return true;
int range = nums[cur];
int i = 0;
while (i <= range) {
if (i >= nums.size() - 1) {
return true;
}
if (i + nums[i] > range) {
range = nums[i] + i;
}//范围扩大
++i;
}
return false;
}
};(3)45.跳跃游戏II
这个难一点

?
先第一个元素获取第一个范围,然后在这第一个范围里面找到值最大的数,作为新的范围,如此反复,然后这里说了一定可以跳到最后,所以我们不用担心无解
class Solution {
public:
int jump(vector<int>& nums) {
int cur = 0;
if (nums.size() <= 1) return 0;
int range = nums[cur];
int rs = 1;//第一步肯定要跳
int max = range;
int p = 0;//加快内部的for
while (range<nums.size()-1) {
for (int i = p; i <=range; ++i) {//这里是等于,很重要
if (i + nums[i] > max) {
max = i + nums[i];
}
}
p += range;
range = max;
++rs;
}
return rs;
}
};(4)56. 合并区间

模拟的过程就是贪心啦。
排序然后分情况处理,排序用引用加快速度
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
if (intervals.size()<=1 ){
return intervals;
}
sort(intervals.begin(), intervals.end(), [](const vector<int> &a, const vector<int> &b)->bool {
return a[0] < b[0];//这里按左边界排序
});
vector<vector<int>> rs;
vector<int> temp;
int end = intervals[0][1];
int start = intervals[0][0];
temp.push_back(start);
temp.push_back(end);
for (int i = 1; i < intervals.size(); ++i) {
if (intervals[i][0] <= end) {
if (intervals[i][1] > end) {
end = intervals[i][1];
}
temp.pop_back();
temp.push_back(end);
}
else {
rs.push_back(temp);
temp.clear();
start = intervals[i][0];
end = intervals[i][1];
temp.push_back(start);
temp.push_back(end);
}
if (i == intervals.size() - 1) {
rs.push_back(temp);
}
}
return rs;
}
};?6.其他
(1)53. 最大子序和?

第一反应用动态规划而不是贪心
dp
/*定义一个函数f(n),以第n个数为结束点的子数列的最大和,
存在一个递推关系f(n) = max(f(n-1) + A[n], A[n]);将这些最大和保存下来后,取最大的那个就是,最大子数组和。
因为最大连续子数组 等价于 最大的以n个数为结束点的子数列和*/
class Solution {
public:
//f_n表示n为终点的最大子数组和
int maxSubArray(vector<int>& nums) {
if (nums.size() == 0)return NULL;
int res = INT_MIN;
int f_n = -1;
for (int i = 0; i < nums.size(); ++i) {
f_n = max(nums[i], f_n + nums[i]);
res = max(f_n, res);
}
return res;
}
};牛逼的!
法二:暴力
class Solution2 {
public:
int maxSubArray(vector<int>& nums) {
int result = INT32_MIN;
int count = 0;
for (int i = 0; i < nums.size(); i++) { // 设置起始位置
count = 0;
for (int j = i; j < nums.size(); j++) { // 每次从起始位置i开始遍历寻找最大值
count += nums[j];
result = count > result ? count : result;
}
}
return result;
}
};法三:贪心
关键在于:不能让“连续和”为负数的时候加上下一个元素,而不是 不让“连续和”加上一个负数。
如果 -2 1 在一起,计算起点的时候,一定是从1开始计算,因为负数只会拉低总和,这就是贪心贪的地方!
局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。
全局最优:选取最大“连续和”
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int result = INT32_MIN;
int count = 0;
for (int i = 0; i < nums.size(); i++) {
count += nums[i];
if (count > result) { // 取区间累计的最大值(相当于不断确定最大子序终止位置)
result = count;
}
if (count <= 0) count = 0; // 相当于重置最大子序起始位置,因为遇到负数一定是拉低总和
}
return result;
}
};(2)134. 加油站

?很妙的解法,看代码来体会,这题我是不会的
class Solution {
public:
int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
int rest = 0, run = 0, start = 0;
//rest是计算是否有解的,也就是说如果没有解,其实就是所有的gas加起来小于cost
//run代表实时的油量
//start就是起点
for (int i = 0; i < gas.size(); ++i) {
run += (gas[i] - cost[i]);
rest += (gas[i] - cost[i]);
if (run < 0) {
start = i + 1;//为什么不是i?因为如果run此时小于0了就说明i-i+1这一段的cost大于之前剩余的油量加上第i站加油站的油量
//所以必须是i+1
run = 0;
}
}
return rest < 0 ?
-1 : start;
}
};当然还有个暴力的:
//暴力
class Solution2 {
public:
? ? int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
? ? ? ? for (int i = 0; i < cost.size(); i++) {
? ? ? ? ? ? int rest = gas[i] - cost[i]; // 记录剩余油量
? ? ? ? ? ? int index = (i + 1) % cost.size();
? ? ? ? ? ? while (rest > 0 && index != i) { // 模拟以i为起点行驶一圈
? ? ? ? ? ? ? ? rest += gas[index] - cost[index];
? ? ? ? ? ? ? ? index = (index + 1) % cost.size();
? ? ? ? ? ? }
? ? ? ? ? ? // 如果以i为起点跑一圈,剩余油量>=0,返回该起始位置
? ? ? ? ? ? if (rest >= 0 && index == i) return i;
? ? ? ? }
? ? ? ? return -1;
? ? }
};
(3)968.监控二叉树

?每个节点有三种状态:节点上有摄像机,节点没摄像机但是被摄像机覆盖,节点没摄像机也没被覆盖。
// 版本一
class Solution {
private:
int result;
int traversal(TreeNode* cur) {
// 空节点,该节点有覆盖
if (cur == NULL) return 2;
int left = traversal(cur->left); // 左
int right = traversal(cur->right); // 右
// 情况1
// 左右节点都有覆盖
if (left == 2 && right == 2) return 0;
// 情况2
// left == 0 && right == 0 左右节点无覆盖
// left == 1 && right == 0 左节点有摄像头,右节点无覆盖
// left == 0 && right == 1 左节点有无覆盖,右节点摄像头
// left == 0 && right == 2 左节点无覆盖,右节点覆盖
// left == 2 && right == 0 左节点覆盖,右节点无覆盖
if (left == 0 || right == 0) {
result++;
return 1;
}
// 情况3
// left == 1 && right == 2 左节点有摄像头,右节点有覆盖
// left == 2 && right == 1 左节点有覆盖,右节点有摄像头
// left == 1 && right == 1 左右节点都有摄像头
// 其他情况前段代码均已覆盖
if (left == 1 || right == 1) return 2;
// 以上代码我没有使用else,主要是为了把各个分支条件展现出来,这样代码有助于读者理解
// 这个 return -1 逻辑不会走到这里。
return -1;
}
public:
int minCameraCover(TreeNode* root) {
result = 0;
// 情况4
if (traversal(root) == 0) { // root 无覆盖,判断根节点
result++;
}
return result;
}
};简化后:
// 版本二
class Solution {
private:
int result;
int traversal(TreeNode* cur) {
if (cur == NULL) return 2;
int left = traversal(cur->left); // 左
int right = traversal(cur->right); // 右
if (left == 2 && right == 2) return 0;
else if (left == 0 || right == 0) {
result++;
return 1;
}
else return 2;
}
public:
int minCameraCover(TreeNode* root) {
result = 0;
if (traversal(root) == 0) { // root 无覆盖
result++;
}
return result;
}
};
