目录
一、链表概述
1.相关定义
- 链表:线性表的链式存储结构称为链表
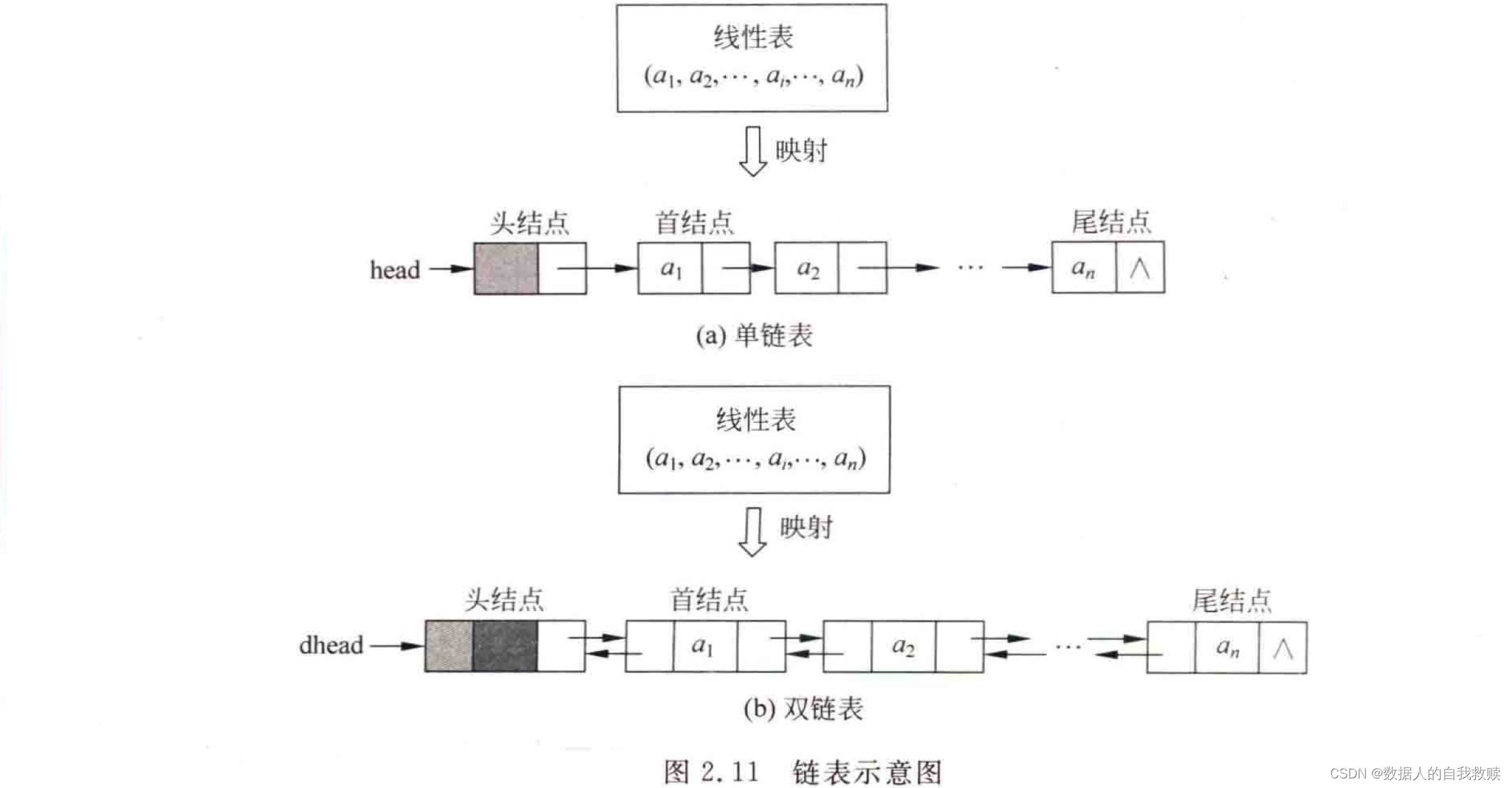
- 单链表:在每个结点中除包含有数据域以外只设置一个指针域,用于指向其后继结点,这样构成的链表称为线性单向链接表,简称为单链表。
- 双链表:在每个节点中除包含有数值域以外设置两个指针域,分别用于指向其前驱结点和后继结点,这样构成的链表称为线性双向链表,简称为双链表。
- 头指针:在线性表的链式存储中,通常每个链表带有一个头结点,并通过头结点的指针唯一标识该链表,称之为头指针。
- 首指针:指向首结点或者开始结点的指针称为首指针。
- 尾指针:指向尾结点的指针称为尾指针
?二、单链表
? ? ? ? 在单链表中,假设每个结点的类型用LinkNode表示,它应包括存储元素的数据域,这里用data表示,其类型用通用类型标识符ElemType表示,还包括存储后继结点位置的指针域,这里用next表示。LinkNode类型的声明如下:
typedef struct LNode
{
ElemType data; //存放元素值
struct LNode *next; //指向后继结点
}LinkNode; //单链表结点类型? ? ? ? 为了简单,假设ElemType为int类型,使用以下自定义类型语句:
typedef int ElemType;1.插入和删除节点的操作
(1)插入结点
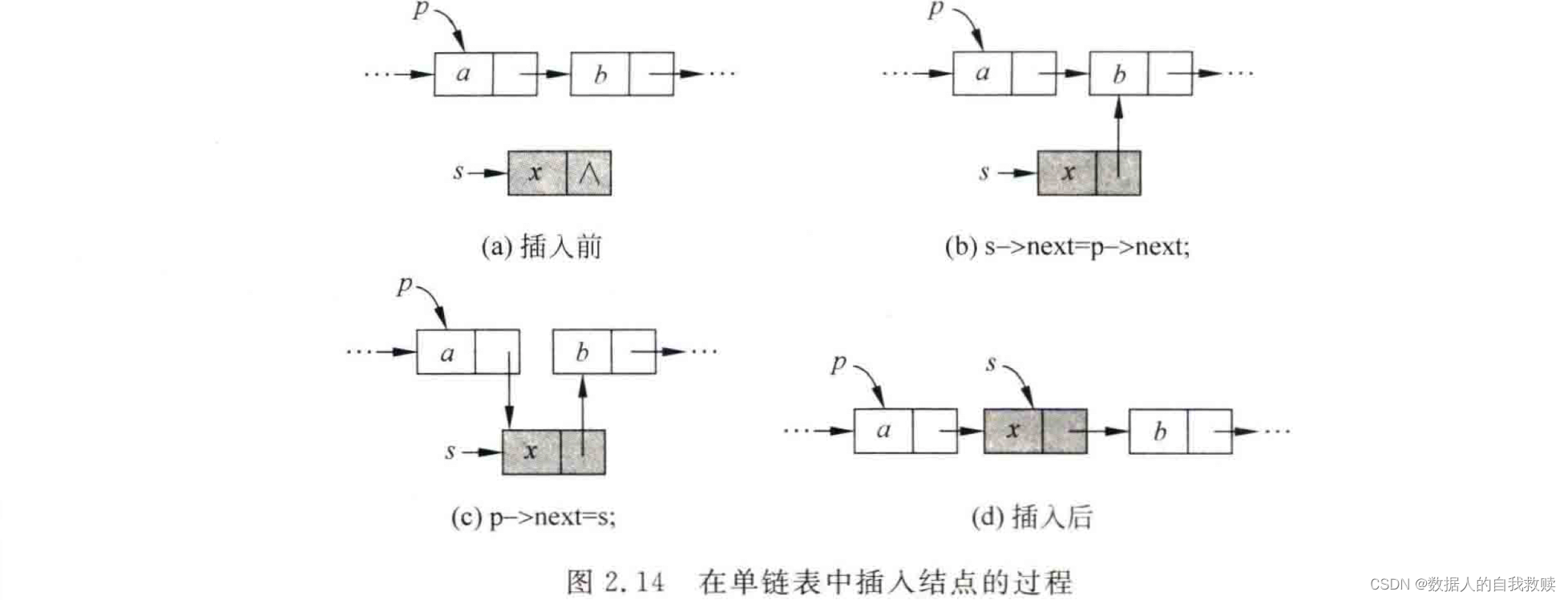
s->next=p->next;
p->next=s;(2)删除结点

p->next=p->next->next;? ? ? ? ?一般情况下,在删除一个结点后还需要释放其存储空间,实现删除上述b结点并释放其存储空间的语句描述如下 :
q=p->next; //q临时保存被删结点
p->next=q->next; //从链表中删除结点q
free(q); //释放结点q的空间2.建立单链表
(1)头插法

void CreatList(LinkNode *&L,ElemType a[],int n)
{
LinkNode *s;
L=(LinkNode *)malloc(sizeof(LinkNode));
L->next=NULL; //创建头结点,其next域置为NULL
for(int i=0;i<n;i++) //循环建立数据结点s
{
s=(LinkNode *)malloc(sizeof(LinkNode)):
s->data=a[i]; //创建数据结点s
s->next=L->next; //将结点s插入到原首结点之前,头结点之后
L->next=s;
}
}?(2)尾插法

void CreatListR(LinkNode *&L,ElemType a[],int n)
{
LinkNode *s,*r;
L=(LinNode *)malloc(sizeof(LinkNode)); //创建头结点
r=L; //r始终指向尾结点,初始时指向头结点
for(int i=0;i<n;i++) //循环建立数据结点
{
s=(LinkNode *)malloc(sizeof(LinkNode));
s->data=a[i]; //创建数据结点s
r->next=s; //将结点s插入到结点r之后
r=s;
}
r->next=NULL; //尾结点的next域置为NULL
}3.线性表基本运算在单链表中的实现
(1)初始化线性表InitList(&L)
void InitList(LinkNode *&L)
{
L=(l=LinkNode *)malloc(sizeof(LinkNode));
L->next=NULL; //创建头结点,其next域置为NULL
}(2)销毁线性表DestroyList(&L)
? ? ? ? 该运算释放单链表L占用的内存空间,即逐一释放全部结点空间。

void DestroyList(LinkNode *&L)
{
LinkNode *pre=L,*p=L->next; //pre指向结点p的前驱节点
while(p!=NULL) //扫描单链表L
{
free(pre); //释放pre结点
pre=p; //pre、p同步后移一个结点
p=pre->next;
}
free(pre); //循环结束时p为NULL,pre指向尾结点,释放它
}(3)判断线性表是否为空集ListEmpty(L)
bool ListEmpty(LinkNode *L)
{
return(L->next==NILL);
}(4)求线性表的长度ListLength(L)
? ? ? ? 该运算返回单链表L中数据结点的个数。
int ListLength(LinkNode *L)
{
int n=0;
LinkNode *p=L; //p指向头结点,n置为0(即头结点的序号为0)
while(p->next!=NULL)
{
n++;
p=p->next;
}
return(n); //循环结束,p指向尾结点,其序号n为结点个数
}(5)输出线性表DispList(L)
? ? ? ? 该运算逐一扫描单链表L的每个数据结点,并显示各结点的data值域。
void DispList(LinkNode *L)
{
LinkNode *p=L->next; //p指向首结点
while(p!=NULL) //p不为NULL,输出p结点的data域
{
printf("%d",p->data);
p=p->next; //p移向下一个结点
}
printf("\n");
}(6)求线性表中某个数据元素值GetElem(L,i,e)
? ? ? ? 该运算在单链表L中从头开始找到第i个结点,若存在第i个数据结点,则将其data域值赋给变量e。
bool GetElem(LinkNode *L,int i,ElemType &e)
{
int j=0;
LinkNode *p=L; //p指向头结点,j置为0(即头结点的序号为0)
if(i<=0) return false; //i错误返回假
while(j<i&&p!=NULL) //找第i个结点p
{
j++;
p=p->next;
}
if(p==NULL) //不存在第i个数据结点,返回false
return false;
else
{
e=p->data;
return true; //存在第i个数据结点,返回true
}
}(7)按元素值查找LocateElem(L,e)
int LocateElem(LinkNode *L,ElemType e)
{
int i=1;
LinkNode *p=L->next; //p指向首结点,i置为1(即首结点的序号为1)
while(p!=NULL&&p->data!=e) //查找data值为e的结点,其序号为i
{
p=p->next;
i++;
}
if(p==NULL) return(0); //不存在值为e的结点,返回0
else return(i); //存在值为e的结点,返回其逻辑序号
}(8)插入数据元素ListInsert(&L,i,e)
bool LinstInsert(LinkNode *&L,int i,ElemType e)
{
int j=0;
LinkNode *p=L,*s; //p指向头结点,j置为0(即头结点的序号为0)
if(i<=0) return false; //i错误返回false
while(j<i-1&&p!=NULL) //查找第i-1个结点p
{
j++;
p=p->next;
}
if(p==NULL) //未找到第i-1个结点,返回false
return false;
else //找到第i-1个结点p,插入新结点并返回true
{
s=(LinkNode *)malloc(sizeof(LinkNode));
s->data=e; //创建新结点s,其data域置为e
s->next=p->next; //将结点s插入到结点p之后
p->next=s;
return true;
}
}(9)删除数据元素LinkDelete(&L,i,e)
bool ListDelete(LinkNode *&L,int i,ElemType &e)
{
int j=0;
LinkNode *p=L,*q;
if(i<=0) return false;
while(j<i-1&&p!=NUll)
{
j++;
p=p->next;
}
if(p==NULL)
return false;
else
{
q=p->next;
if(q==NULL)
return false;
e=q->data;
p->next=q->next;
free(q);
return true;
}
}4.单链表应用举例
- 有一个带头结点的单链表
,设计一个算法将其拆分成两个带头结点的单链表L1和单链表L2,其中
,
,要求L1使用L的头结点。
void split(LinkNode *&L,LinkNode *&L1,LinkNode *&L2)
{
LinkNode *p=L->next,*q,*r1; //p指向第一个数据结点
L1=L; //L1利用原来L的头结点
r1=L1; //r1始终指向L1的尾结点
L2=(LinkNode *)malloc(sizeof(LinkNode)); //创建L2的头结点
L2->next=NULL; //置L2的指针域为NULL
while(p!=NULL)
{
r1->next=p; //采用尾插法将*p(data值为ai)插入L1中
r1=p;
p=p->next; //p移动到下一个结点(data值为bi)
q=q->next; //头插法会修改结点p的next域,用q保存结点p的后继结点
p->next=L2->next; //采用头插法将结点p插入L2中
L2->next=p;
p=q; //p重新指向ai+1的结点
}
r1->next=NULL; //尾结点next置空
}- 设计一个算法,删除一个单链表L中元素值最大的结点(假设这样的结点唯一)
void delmaxnode(LinNode *&L)
{
LinkNode *P=L->next,*maxp=p,*maxpre=pre;
while(P!=NULL) //用p扫描整个单链表,pre始终指向其前驱节点
{
if(maxp->data<p->data) //若找到一个更大的结点
{
maxp=p; //更新maxp
maxpre=pre; //更新maxpre
}
pre=p; //p、pre同步后移一个结点
p=p->next;
}
maxpre->next=maxp->next; //删除maxp结点
free(maxp); //释放maxp结点
}- 有一个带头结点的单链表L(至少有一个数据结点),设计一个算法使其元素递增有序排列
void sort(LinkNode *&L)
{
LinkNode *p,*pre,*q;
p=L->next->next; //p指向L的第二个数据结点
L->next->next=NULL; //构造只含一个数据结点的有序单链表
while(p!=NULL)
{
q=p->next; //q保存p结点后继结点的指针
pre=L; //从有序单链表开头进行比较,pre指向插入结点的前驱结点
while(pre->next!=NULL&&pre->next->data<p->data)
pre=pre->next; //在有序单链表中找插入p所指结点的前驱结点(pre所指向)
p->next=pre->next; //在pre所指结点之后插入p所指结点
pre->next=p;
p=q; //扫描原单链表余下的结点
}
}三、双链表
? ? ? ? 对于双链表,采用类似于单链表的类型声明,其结点类型DLinkNode的声明如下:
typedef struct DNode
{
ElemType data; //存放元素值
struct DNode *prior; //指向前驱结点
struct DNode *next; //指向后继结点
}DLinkNode; //双链表的结点类型1.建立双链表
(1)头插法
void CreatListF(DLinkNode *&L,ElemType a[],int n) //采用头插法建立双链表
{
DLinkNode *s;
L=(DLinkNode *)malloc(sizeof(DlinkNode)); //创建头结点
L->prior=L->next=NULL; //前后指针域置为NULL
for(int i=0;i<n;i++) //循环建立数据结点
{
s=(DLinkNode *)malloc(sizeof(DLinkNode));
s->data=a[i]; //创建数据结点s
s->next=L->next; //将s结点插入到头结点之后
if(L->next!=NULL) //若L存在数据结点,修改L->next的前驱指针
L->next->prior=s;
L->next=s;
s->prior=L;
}
}(2)尾插法
void CreatListR(DLinkNode *&L,ElemType a[],int n) //采用尾插法建立双链表
{
DLinkNode *s,*r;
L=(DLinkNode *)malloc(sizeof(DLinkNode)); //创建头结点
r=L; //r始终指向尾结点,开始时指向头结点
for(int i=0;i<n;i++) //循环建立数据结点
{
s=(DLinkNode *)malloc(sizeof(DLinkNode));
s->data=a[i]; //创建数据结点s
r->next=s;s->prior=r; //将s结点插入到r结点之后
r=s; //r指向尾结点
}
r->next=NULL; //尾结点的next域置为NULL
}2.线性表基本运算在双链表中的实现
(1)插入结点
bool ListInsert(DLinkNode *&L,int i,ElemType e)
{
int j=0;
DLinkNode *p=L,*s;
if(i<=0) return false;
while(j<i-1&&p!=NULL)
{
j++;
p=p->next;
}
if(p==NULL)
return false;
else
{
s=(DLinkNode *)malloc(sizeof(DlinkNode));
s->data=e;
s->next=p->next;
if(p->next!=NULL)
p->next->prior=s;
s->prior=p;
p->next=s;
return true;
}
}(2)删除结点
bool ListDelete(DLinkNode *&L,int i,ElemType &e)
{
int j=0;
DLinkNode *p=L,*q;
if(i<=0) return false;
while(j<i-1&&p!=NULL)
{
j++;
p=p->next;
}
if(p==NULL)
return false;
else
{
q=p->next;
if(q==NULL)
return false;
e=q->data;
p->next=q->next;
if(p->next!=NULL)
p->next->prior=p;
free(q);
return true;
}
}3.双链表应用举例
- 有一个带头结点的双链表L,设计一个算法将其所有元素逆置。
? ? ? ? 先构造只有一个头结点的空双链表L(利用原来的头结点),用p扫描双链表的所有数据结点,采用头插法将p所指结点插入到L中。
void reverse(DLinkNode *&L)
{
DLinkNode *p=L->next,*q;
L->next=NULL;
while(p!=NULL)
{
q=p->next;
p->next=L->next;
if(L->next!=NULL)
L->next->prior=p;
L->next=p;
p->prior=L;
p=q;
}
}- 有一个带头结点的双链表L(至少有一个数据结点),设计一个算法时期元素递增有序排列
void sort(DLinkNode *&L)
{
DLinkNode *p,*pre,*q;
p=L->next->next;
L->next->next=NULL;
while(p!=NULL)
{
q=p->next;
pre=L;
while(pre->next!=NULL&&pre->next->data<p->data)
pre=pre->data;
p->next=pre->next;
if(pre->next!=NULL)
pre->next->prior=p;
pre->next=p;
p->prior=pre;
p=q;
}
}四、循环链表
1.相关概念
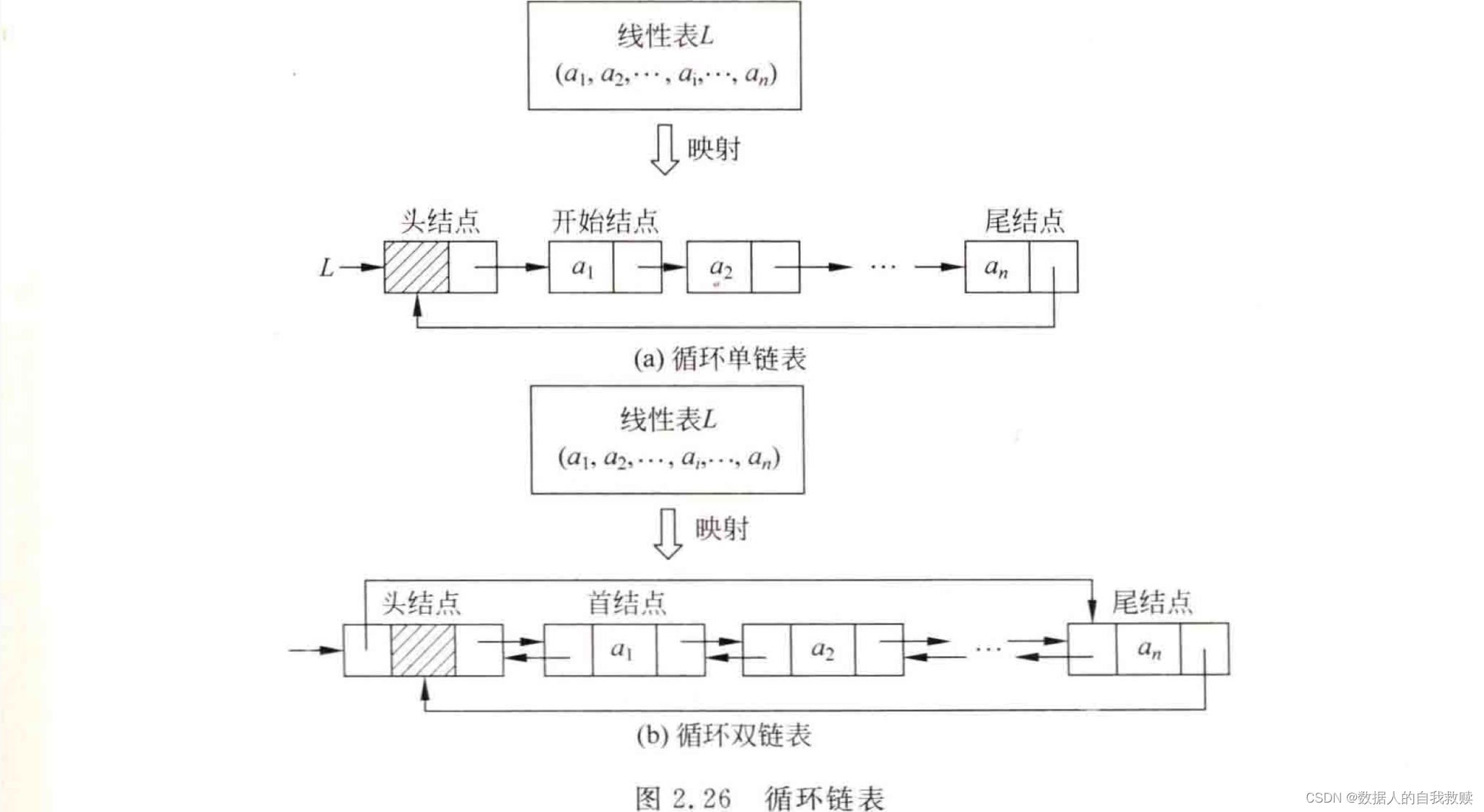
? ? ? ? 循环链表是另一种形式的链式存储结构。循环链表又循环单链表和循环双链表两种类型,循环单链表的结点类型和非循环单链表的结点类型LinkNode相同,循环双链表的结点类型和非循环双链表的结点类型DLinkNode相同。
? ? ? ? 把单链表改为循环单链表的过程是将他的尾结点next指针域由原来为空改为指向头结点,整个单链表形成一个环。由此,从表中任一结点出发均可找到链表中的其他结点。
? ? ? ? 把双链表改为循环双链表的过程是将它的尾结点next指针域由原来为空改为指向头结点,将它的头结点prior指针域改为指向尾结点,整个双链表形成两个环。
?2.例题
- 有一个带头结点的循环单链表L,设计一个算法统计其data域值为x的结点个数
int count(LinkNode *L,ElemType x)
{
int i=0;
LinkNode *p=L->next;
while(p!=L)
{
if(p->data==x)
i++;
p=p->next;
}
return i;
}- 有一个带头结点的循环双链表。设计一个算法删除第一个data域值为x的结点
bool delelem(DLinkNode *&L,ElemType x)
{
DLinkNode *p=L->next;
while(p!=L&&p->data!=x)
p=p->next;
if(p!=L)
{
p->next->prior=p->prior;
p->prior->next=p->next;
free(p);
return true;
}
else
return false;
}- 设计一个算法,判断带头结点的循环双链表L(含两个以上的结点)中的数据结构是否对称
bool Symm(DLinkNode *L)
{
bool same=true;
DLinkNode *p=L->next;
DLinkNode *q=L->prior;
while(same)
{
if(p->data!=q->data)
same=false;
else
{
if(p==q||p==q->prior) break;
q=q->prior;
p=p->next;
}
}
return same;
}