LC.454 中等题
给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足:
0 <= i, j, k, l < n
nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0
分析:暴力思路:直接遍历枚举,判断某个组合是否满足要求,满足则count++;这样做的时间复杂度为n^4,说明一定还有更好的方法,
只能是空间换时间,我们遍历前两个数组,将每一种组合存入map中,key为nums[i]+nums[j],value为nums[i]+nums[j]出现的次数,然后再遍历后两个数组,判断0-(num[k]+nums[l]),是否在map中出现过,出现过则count+value;
class Solution {
public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
HashMap<Integer,Integer> map =new HashMap<>();
for(int i = 0;i<nums1.length;i++){
for(int j = 0;j<nums2.length;j++){
if(map.containsKey(nums1[i]+nums2[j])){
map.put(nums1[i]+nums2[j],map.get(nums1[i]+nums2[j])+1);
}else{
map.put(nums1[i]+nums2[j],1);
}
}
}
int count =0;
for(int i=0;i<nums3.length;i++){
for(int j=0;j<nums4.length;j++){
int temp=0-(nums3[i]+nums4[j]);
if(map.containsKey(temp)){
count+=map.get(temp);
}
}
}
return count;
\
}
}
LC.383 与LC.242 有效字母异位词几乎一样
class Solution {
public boolean canConstruct(String ransomNote, String magazine) {
int[] arr =new int[26];
for(int i=0;i<magazine.length();i++){
arr[magazine.charAt(i)-'a']++;
}
for(int i=0;i<ransomNote.length();i++){
arr[ransomNote.charAt(i)-'a']--;
}
for(int i=0;i<arr.length;i++){
if(arr[i]<0){
return false;
}
}
return true;
}
}
LC.15 三数之和
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
分析:
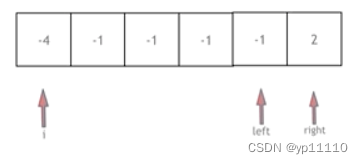
拿这个nums数组来举例,首先将数组排序,然后有一层for循环,i从下标0的地方开始,同时定一个下标left 定义在i+1的位置上,定义下标right 在数组结尾的位置上。
依然还是在数组中找到 abc 使得a + b +c =0,我们这里相当于 a = nums[i],b = nums[left],c = nums[right]。
接下来如何移动left 和right呢, 如果nums[i] + nums[left] + nums[right] > 0 就说明 此时三数之和大了,因为数组是排序后了,所以right下标就应该向左移动,这样才能让三数之和小一些。
如果 nums[i] + nums[left] + nums[right] < 0 说明 此时 三数之和小了,left 就向右移动,才能让三数之和大一些,直到left与right相遇为止
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> result =new ArrayList<>();
Arrays.sort(nums);
for(int i=0;i<nums.length;i++){
if(nums[0]>0){return result;}//排序过后 首相如果大于0 则说明数组中没有符合条件的三元组
if(i>0 && nums[i-1]==nums[i]){continue;}//去重
int left = i+1;
int right =nums.length-1;
while(left<right){
if(nums[i]+nums[left]+nums[right]>0){
right--;
}
else if(nums[i]+nums[left]+nums[right]<0){
left++;
}else{
result.add(Arrays.asList(nums[i],nums[left],nums[right]));
while(right>left && nums[right]==nums[right-1]){//去重
right--;
}
while(right>left&&nums[left]==nums[left+1]){//去重
left++;
}
right--;
left++;
}
}
}
return result;
}
}
说到去重,其实主要考虑三个数的去重。 a, b ,c, 对应的就是 nums[i],nums[left],nums[right]
a 如果重复了怎么办,a是nums里遍历的元素,那么应该直接跳过去。
但这里有一个问题,是判断 nums[i] 与 nums[i + 1]是否相同,还是判断 nums[i] 与 nums[i-1] 是否相同。
有同学可能想,这不都一样吗。
其实不一样!
都是和 nums[i]进行比较,是比较它的前一个,还是比较他的后一个。
如果我们的写法是 这样:
if (nums[i] == nums[i + 1]) { // 去重操作
continue;
}
那就我们就把 三元组中出现重复元素的情况直接pass掉了。 例如{-1, -1 ,2} 这组数据,当遍历到第一个-1 的时候,判断 下一个也是-1,那这组数据就pass了。
我们要做的是 不能有重复的三元组,但三元组内的元素是可以重复的!
所以这里是有两个重复的维度。
那么应该这么写:
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
这么写就是当前使用 nums[i],我们判断前一位是不是一样的元素,在看 {-1, -1 ,2} 这组数据,当遍历到 第一个 -1 的时候,只要前一位没有-1,那么 {-1, -1 ,2} 这组数据一样可以收录到 结果集里。
这是一个非常细节的思考过程。
b与c的去重 也就是nums[left],nums[right]的去重,
当某一时刻a+b+c==0满足条件时候,就需要判断left+1位置的元素和right-1位置的元素与当前位置元素是否相等,相等则++;
LC18 四数之和
给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应,则认为两个四元组重复):
0 <= a, b, c, d < n
a、b、c 和 d 互不相同
nums[a] + nums[b] + nums[c] + nums[d] == target
你可以按 任意顺序 返回答案 。
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
List<List<Integer>> list =new ArrayList<>();
Arrays.sort(nums);
for(int k=0;k<nums.length;k++){
//剪枝
if(nums[k]>target && nums[k]>0){
return list;
}
//去重
if(k>0&&nums[k-1]==nums[k]){
continue;
}
for(int i =k+1;i<nums.length;i++){
// //剪枝
// if(nums[k]+nums[i]>target){
// return list;
// }
//去重
if(i>k+1 && nums[i-1]==nums[i]){
continue;
}
int left =i+1;
int right =nums.length-1;
while(right>left){
int sum =nums[k]+nums[i]+nums[left]+nums[right];
if(sum>target){
right--;
}else if(sum<target){
left++;
}else{
list.add(Arrays.asList(nums[k],nums[i],nums[left],nums[right]));
while(right>left && nums[right-1]==nums[right]){
right--;
}
while(right>left && nums[left+1]==nums[left]){
left++;
}
left++;
right--;
}
}
}
}
return list;
}
}
本题与三数之和类似,只不过去重和剪枝操作需要更细心,先对数组进行排序,依旧是遍历数组,变量k作为最外层遍历,如果nums[k]>=target ,那么也没有必要继续往后遍历了,直接返回当前list,然后是去重,还是后一个与前一个比较,nums[k-1]==nums[k]; 思路一样,把握好剪枝和去重的细节,才能正确通过。