基础数据结构
数据结构:数据的存储方式。
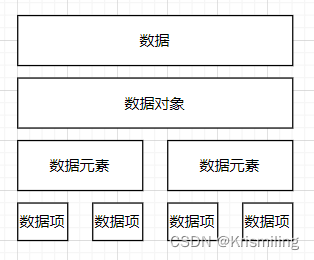
- 数据:信息的载体,是描述客观事物属性的数、字符及所有能输入到计算机中并被计算机程序识别和处理的符号的集合。
- 数据对象:具有相同性质的数据元素的集合,是数据的一个子集。
- 数据元素:数据的基本单位,通常作为一个整体进行考虑和处理。
- 数据项:构成数据元素的不可分割的最小单位。
数据结构的三要素
逻辑结构:分为线性结构、集合、树形结构、图状结构。集合、树形结构、图状结构统称为非线性结构。
物理结构(存储结构):顺序存储、链式存储、索引存储、散列/哈希存储。
栈与队列
执行顺序:栈 - 先入后出, 队列 - 先入先出。
//面试题:实现一个栈
class Stack {
constructor() {
this.items = [];
}
//添加新元素到栈顶
push(element) {
this.items.push(element);
}
//移出栈顶
pop() {
return this.items.pop();
}
//返回栈顶元素
peek() {
return this.items[this.items.length - 1];
}
//是否为空
isEmpty() {
return this.items.length === 0;
}
//移出栈内所有元素
clear() {
this.items = [];
}
//大小
size() {
return this.items.length;
}
}
算法流程
1. 需要什么样的数据结构、满足模型的数据 —— 构造变量 & 常量
2. 运行方式:简单的条件执行、遍历、递归 —— 算法主体结构
3. 确定输入输出:确定流程
//判断括号是否有效自闭合
const isValid = function(s) {
const stack = new Stack();
const map = {
'}': '{',
']': '[',
')': '('
};
for(let i = 0; i < s.length; i++) {
const char = s[i];
stack.push(char);
if(stack.size < 2)
continue;
const theLastOne = stack[stack.size - 1];
const theLastTwo = stack[stack.size - 2];
if(map[theLastOne] === theLastTwo) {
stack.pop();
stack.pop();
}
}
return stack.size === 0;
}
数组和链表
- 查找:数组连续、效率高。
- 数组可以迅速定位到数组中某一个节点的位置。
- 链表则通过前一个元素指向下一个元素,需要前后依赖顺序查找,效率较低。
- 插入:
- 数组插入元素后,后序所有元素的索引都会受到影响和改变。
- 链表由于其指向属性的原因,只要改变前一项和当前被插入项的指向即可完成插入。
//面试题:实现一个链表
//辅助类
class Node {
constructor(element) {
this.element = element;
this.next = null;
}
}
class LinkedList {
constructor() {
this.length = 0;
this.head = null;
}
//返回索引对应的元素
getElementAt(position) {
if(position < 0 || position >= this.length)
return null;
let _current = this.head;
for(let i = 0; i < position; i++) {
_current = _current.next;
}
return _current;
}
//添加节点
append(element) {
let _node = new Node(element);
if(this.head === null) {
this.head = _node;
}else {
let _current = this.getElementAt(this.length - 1);
_current.next = _node;
}
this.length++;
}
//指定位置插入节点
insert (position, element) {
if(position < 0 || position > this.length)
return false;
let _node = new Node(element);
if(position === 0) {
_node.next = this.head;
this.head = _node;
}else {
let _previous = this.getElementAt(position - 1);
_node.next = _previous.next;
_previous.next = _node;
}
this.length++;
return true;
}
//删除对应元素
removeAt (position) {
if(position < 0 || position > this.length)
return false;
let _current = this.head;
if(position === 0) {
this.head = _current.next;
}else {
let _previous = this.getElementAt(position - 1);
_current = _previous.next;
_previous.next = _current.next;
}
this.length--;
return _current.element;
}
//查找元素
indexOf(element) {
let _current = this.head;
for(let i = 0; i < this.length; i++) {
if(_current.element === element)
return i;
_current = _current.next;
}
return -1;
}
}
哈希表
//面试题:哈希表 - 快速匹配定位 - 罗马字符翻译
// I 1
// II 2
// III 3
// IV 4 * => 特殊点的特征先小后大
// V 5
// VI 6
// X 10
// L 50
// C 100
//算法思路:
//从右到左遍历每一个字符:如果右侧<=左侧通过字符映射枚举即可直接翻译取值,就是VIII = 5 + 1 + 1 + 1 = 8;如果右侧>左侧,只有一种相似情况,就是V-I = 5 - 1 = 4。以上两种情况综合即可一次循环求出值。
const MAP = {
'I': 1,
'V': 5,
'X': 10,
'L': 50,
'C': 100
}
const romanToInt = function(s) {
let len = s.length;
let max = 0;
let res = 0;
while(len--) {
let num = MAP[s[len]];
if(max > num) {
res -= num;
continue;
}
max = num;
res += num;
}
return res;
}
树结构
前序遍历(中左右)、中序遍历(左中右)、后序遍历 (左右中)
//遍历二叉树
class Node {
constructor(node) {
this.left = node.left;
this.right = node.right;
this.value = node.value;
}
}
const PreOrder = function(node) {
if (node !== null) {
console.log(node.value);
PreOrder(node.left);
PreOrder(node.right);
}
}
const InOrder = function(node) {
if (node !== null) {
InOrder(node.left);
console.log(node.value);
InOrder(node.right);
}
}
const PostOrder = function(node) {
if (node !== null) {
PostOrder(node.left);
PostOrder(node.right);
console.log(node.value);
}
}
//面试题:搜索二叉树 / 查找二叉树
// 1. 左子树非空时, 左节点的所有值小于根节点
// 2. 右子树非空时, 右节点的所有值大于根节点
// 3. 左右子树分别都是一个搜索二叉树
function findNode(root, value) {
if(root === undefined || root === null) {
return null;
}
if(root.value > value) {
return findNode(root.leftNode, value);
}
if(root.value < value) {
return findNode(root.rightNode, value);
}
if(root.value === value) {
return root;
}
}
数据结构和算法的关系
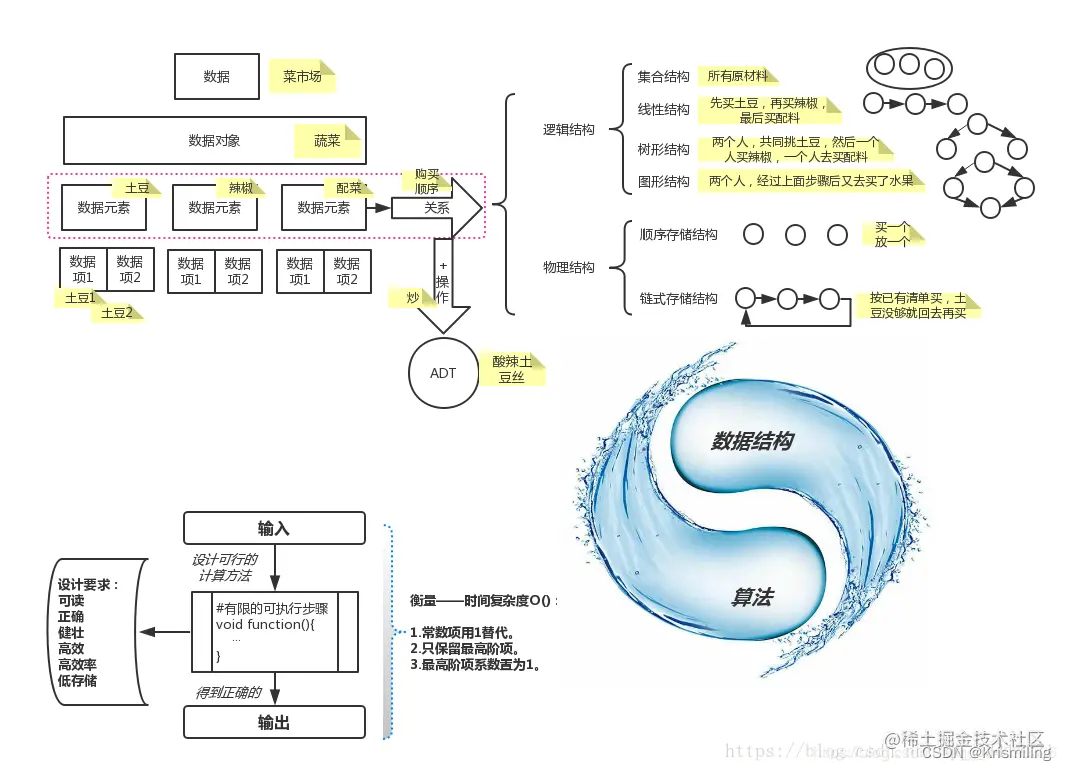
算法复杂度概念
时间复杂度
指执行算法所需要的计算工作量。
- 循环次数最多的代码块
- 最大值原则:多个循环,总复杂度等于最大的代码块的复杂度
- 乘法原则:嵌套的代码复杂度等于嵌套内外代码复杂度乘积
但凡涉及到时间复杂度的问题 => 单层执行、遍历循环、等比变化、委托复合。
空间复杂度
指算法需要消耗的内存空间。
- 常量
- 线性增长O(N)
- log增长
复杂度比较
常数阶O(1) > 对数阶O(logN) > 线性阶O(n) > 线性对数阶O(nlogN) > 平方阶 O(nn) > 立方阶 O(nn*n) > k次方阶 O(n^k)
所以一个好的算法:速度快,存储空间少。
具体算法技巧与概念
分治法D&C
工作原理:
- 找出基线条件
- 不断将问题分解 —— 基线保持一致
- 直到被拆解的问题最终复合基线条件
// 面试题:快排序
// 1. 对数组做一个基线条件定义
// 2. 将数组按照基线条件进行拆分 => 进入下一回合基线条件的查找和定位
// 3. 再次回到第一步
// 4. 退出条件 —— 只剩下基线条件本身
const quickSort = function(arr) {
//4.退出递归 —— 只剩下基线条件本身
if(arr.length <= 1) {
return arr;
}
//1.计算基线
let pivotIndex = Math.floor(arr.length / 2);
let pivot = arr.splice(pivotIndex, 1)[0];
let left = [];
let right = [];
//2.拆分
for(let i = 0; i < arr.length; i++) {
if(arr[i] < pivot) {
left.push(arr[i]);
}else {
right.push(arr[i]);
}
}
//3.回到第一步——递归
return quickSort(left).concat([pivot], quickSort(right));
}
贪婪Greedy
获取利益最大化,始终查找最大项目,尽可能快速满足需求。
//面试题:
// 给定一个整数数组nums,找到一个具有最大和的连续子数组(子数组最少包括一个元素),返回其最大和。
// [1, 2, 3, 5, -9, 2, 10, 22, -30] => 36
//思路:
// 1. 确定数据结构为数组,进行遍历 => 求当前子序列的和 sum, 结果为ans
// 2. 如果sum > 0,则说明sum对结果整体有增益效果 => 则sum保留并且加上当前遍历的数字
// 3. 如果sum <= 0, 这说明对结果无增益效果,舍弃 => sum则直接更新为当前遍历数字
// 4. 每次比较sum 和 ans的大小,将最大值给到ans,遍历结束
const maxSubArray = function(nums) {
let ans = nums[0];
let sum = 0;
for(const num of nums) {
if(sum > 0) {
sum += num;
}else {
sum = num;
}
ans = Math.max(ans, sum);
}
return ans;
}
// 1. => 多重判断 => 序列化产出
// 2. => 优化
// 3. => 数组处理
// 4. => 类型控制 => 对象
动态规划DP
可划分职责领域,下一步规划。
//斐波那契数列 or 杨辉三角 => 推导公式 => 走一步看一步
// F(0) = 0, F(1) = 1
// F(n) = F(n - 1) + F(n - 2), 其中n > 1
//遍历
const fib = function(n) {
if(n < 2) {
return n;
}
let pre = 0, next = 0, result = 1;
for(let i = 2; i < n; i++) {
pre = next;
next = result;
result = pre + next;
}
return result;
}
图Graph
构成:边集合和顶点集合。
分类:有向图、无向图、构造图。
//面试题:实现图类
class Graph {
constructor(v) {
this.vertices = v; // 顶点数
this.edges = 0; // 边集合数
this.arr = [];
// 初始化站点 - 有多少个顶点就有多少个元素
for(let i = 0; i < this.vertices; i++) {
this.arr[i] = [];
}
}
addEdge(v, w) {
this.arr[v].push(w);
this.arr[w].push(v);
this.edges++;
}
showGraph() {
for(let i = 0; i < this.vertices; i++) {
let str = i + '=>';
for(let j = 0; j < this.vertices; j++) {
if (this.arr[i][j] !== undefined) {
str += this.arr[i][j] + '';
}
}
console.log(str);
}
}
}
//图遍历的构造函数
constructor() {
this.marked = [];//已访问过的节点
for(let i = 0; i < this.vertices; i++) {
this.marked[i] = false;
}
}
//解决深度优先 - 一路杀到头,直到最后的顶点,再返回追溯,直到查询路径失败为止
dfs(v) {
this.marked[v] = true;
if(this.arr[v] !== undefined) {
console.log('arrived' + v);
}
(this.arr[v] || []).forEach(w => {
if(!this.marked[w]) {
this.dfs(w);
}
})
}
//图解决广度优先
// 1. 查找相邻顶点
// 2. 取出下一个,加入marked
// 3. 未访问顶点加入未访问
bfs(s) {
let queue = [];
this.marked[s] = true;
queue.push(s);
while(queue.length > 0) {
let v = queue.shift();
if(v !== undefined) {
console.log('arrived' + v);
}
(this.arr[v] || []).forEach(w => {
if(!this.marked[w]) {
this.marked[w] = true;
queue.push(w);
}
})
}
}