目录
????????本文在win10系统的vs2019中验证。
1.二叉搜索树概念
? (1)概念
??????二叉搜索树又称二叉排序树,它只有两种形态:
????????[1]空树
????????[2]满足以下性质的二叉树:
- 若它的左子树不空,则左子树上所有结点的值都小于根节点的值
- 若它的右子树不空,则右子树上所有结点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
? (2)示意图
? ? ? ? 如下是一棵二叉搜索树,左子树结点值均小于根结点,右子树结点值均大于根结点。
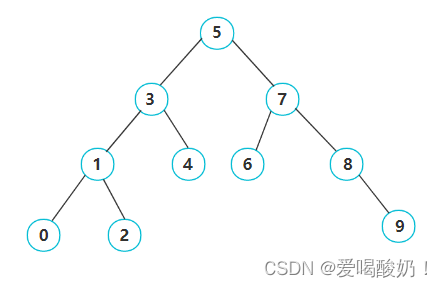
?
2.二叉搜索树次要操作
? (1)二叉搜索树的查找
????????如图是一棵二叉搜索树,需要在树中找到值为9的结点,如何查找?
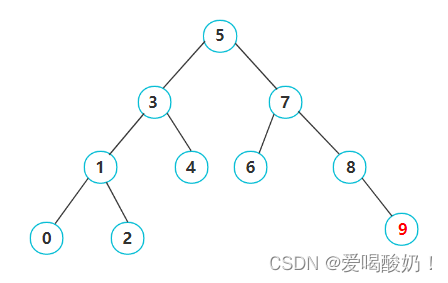
? ? ? ? ?查找方法:[1]首先找到根结点,比较根结点与9的值,如果相等,证明找到了,返回true。
? ? ? ? ? ? ? ? ? ? ? ? ? ?[2]如果根结点的值大于9,那么就去根结点的左子树中找。
? ? ? ? ? ? ? ? ? ? ? ? ? ?[3]如果根结点的值小于9,那么就去根结点的右子树中找。
? ? ? ? 这个方法会不断地向下查找,如果查到最后一个结点都没有找到,说明没有这个结点,返回false。
? (2)二叉搜索树的插入
? ? ? ? 二叉搜索树的插入需要分情况讨论:[1]树是空树 [2]树不是空树
? ? [1]树是空树
? ? ? ? 如果这棵树是空树,那么直接把要插入的元素当作根结点即可。

? ? [2]树不是空树
? ? ? ? 如果树不是空树,那么就需要查找适合这个结点的位置。
????????如图:在原二叉搜索树的基础上插入结点10,这个过程是怎样的?
????????首先将10与根结点比较,10比根结点大,去根结点右子树找。右子树根结点是7,10比7大,去7的右子树找。右子树根结点是8·······,这样依次进行到9这个结点,发现10比9大,但9的右子树是空,那么就10就作为9的右孩子插入。
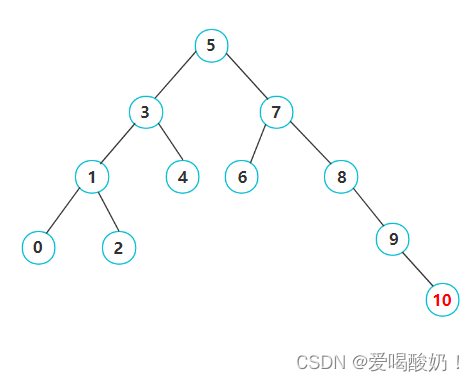
3.二叉搜索树重要操作(删除操作)?
? ? ? ? 二叉搜索树的删除需要考虑很多情况,分为两大类。
? ? ? ? 两大类:(1)要删除的结点有双亲 (2)要删除的结点无双亲
? ? ? ? 其中(1)类还会分两类:<1>要删除的结点是双亲的左孩子 <2>要删除的结点是双亲的右孩子。
? ? ? ? 四小类:[1]要删除的结点没有孩子结点 [2]要删除的结点只有左孩子 [3]要删除的结点只有右孩子 [4]要删除的结点有左右两个孩子
? (1)要删除的结点有双亲
? ?<1>要删除的结点是双亲的左孩子
? ? ? [1]要删除的结点没有孩子结点
? ? ? ? 如图:删除0结点,此时直接删除即可
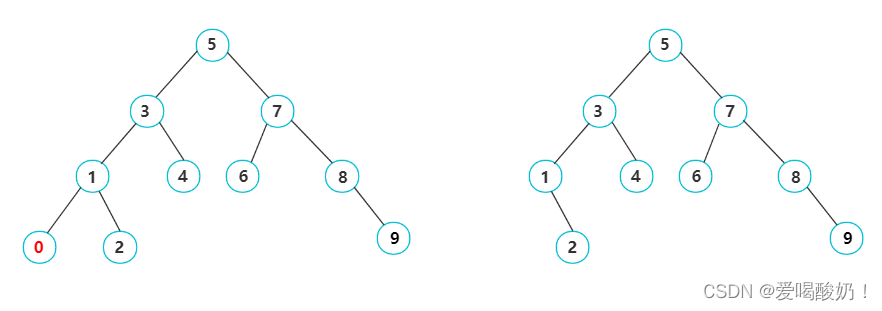
? ? ? [2]要删除的结点只有左孩子
? ? ? ? 如图:删除1结点,此时需要让1结点的双亲结点的左孩子指针指向1结点的左孩子,然后才可以删除1结点。
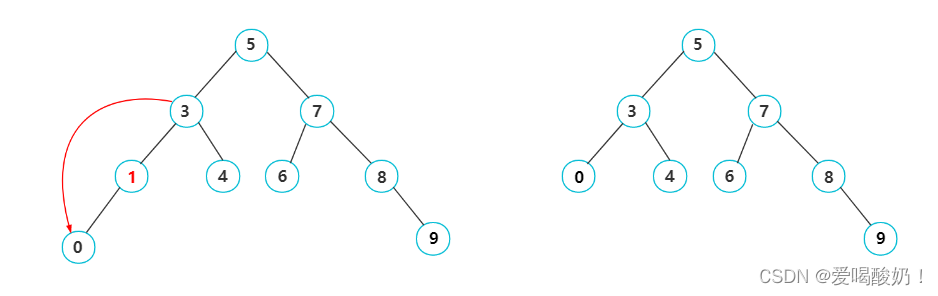
? ? ? [3]要删除的结点只有右孩子
? ? ? ? 如图:删除1结点,此时需要先让1结点的双亲结点的左孩子指针指向1结点的右孩子,然后才可以删除1结点。
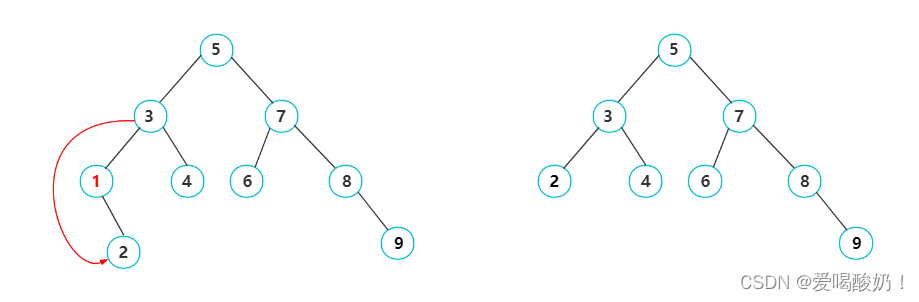
? ? ? [4]要删除的结点有左右两个孩子
? ? ? ? 如图:删除7结点。此时的删除就比较复杂了,我们需要给要删除的结点找到一个替代结点,替代结点有两种找法:1.找要删除的结点的左子树的最大结点(也就是左子树最右侧结点) 2.找要删除的结点的右子树的最小结点(也就是右子树最左侧节点)。
? ? ? ? 我们这里采用的是找左子树最大结点。
????????需要先找到7结点的左子树中最右侧的结点,此时最右侧结点是6.5,然后把6.5的值赋给原本要删除的7结点。
? ? ? ? 此时要删除的那个结点变成了红6.5结点,我们此时只需要删除原本的黑6.5节点即可。
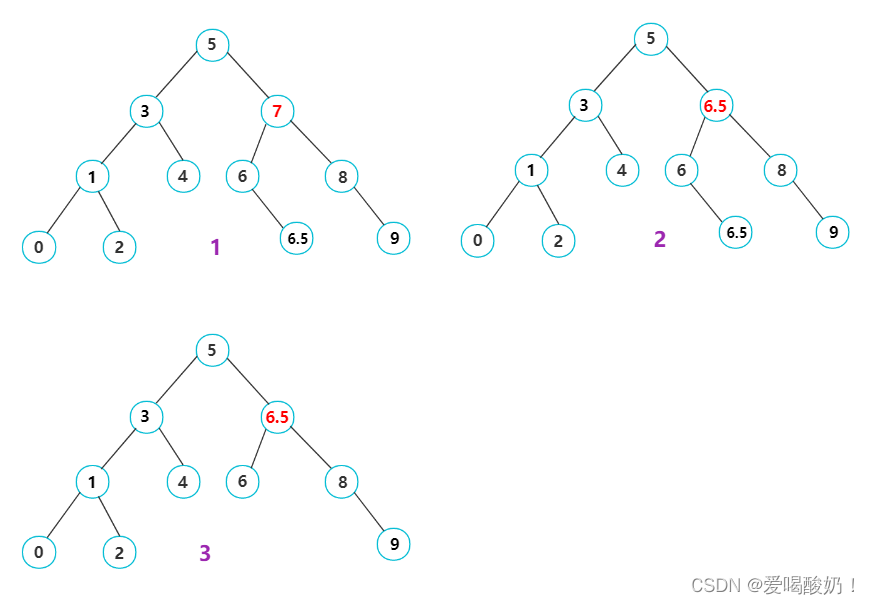
? ?<2>要删除的结点是双亲的右孩子
? ? ? [1]要删除的结点没有孩子结点
????????如图:删除9结点,此时直接删除即可
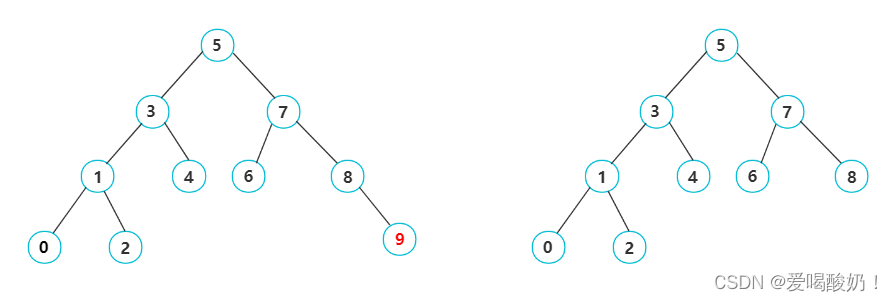
?
? ? ? [2]要删除的结点只有左孩子
? ? ? ? 如图:删除7结点,此时需要让7结点的双亲结点的右孩子指针指向7结点的左孩子,然后才可以删除7结点。
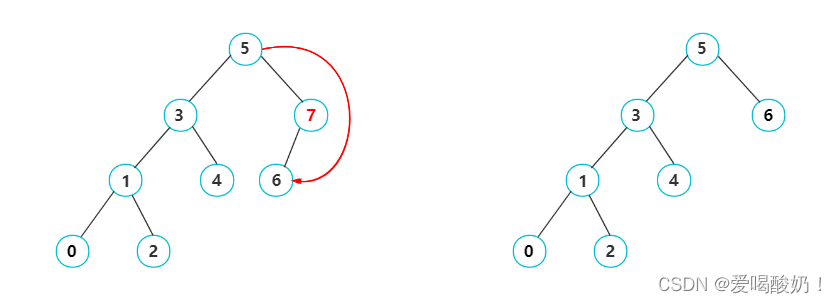
? ? ? [3]要删除的结点只有右孩子
? ? ? ? 如图:删除8结点,此时需要先让8结点的双亲结点的右孩子指针指向8结点的右孩子,然后才可以删除8结点。
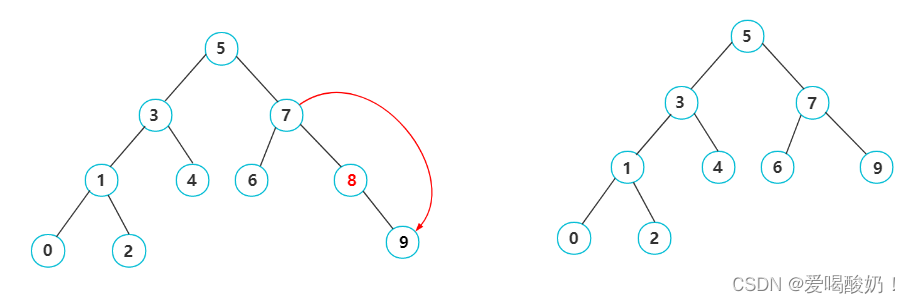
? ? ? [4]要删除的结点有左右两个孩子
? ? ? ? 我们这里采用的是找右子树最小结点。
? ? ? ? 如图:需要删除3结点,3结点右子树最左侧结点是4结点。将替代结点4结点的值赋给3结点,此时的3结点就变成了红4结点。然后删除替代节点黑4结点,删除替代结点的时候替代结点也可能有孩子结点,所以需要让红4结点指向替代结点的孩子结点。
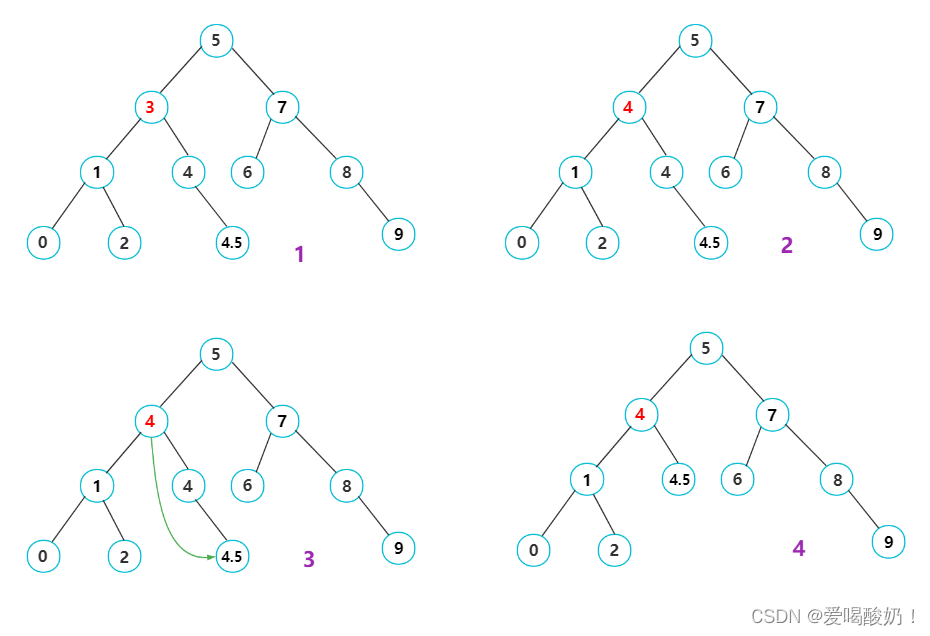
? (2)要删除的结点没有双亲
? ? ? ? 没有双亲结点就只能是根结点。
? ? [1]要删除的结点没有孩子结点
? ? ? ? 此时只存在根结点,直接删除根结点就可。

? ? [2]要删除的结点只有左孩子
? ? ? ? 如图:删除5结点。直接让5结点的左孩子当根结点,删除5结点即可。
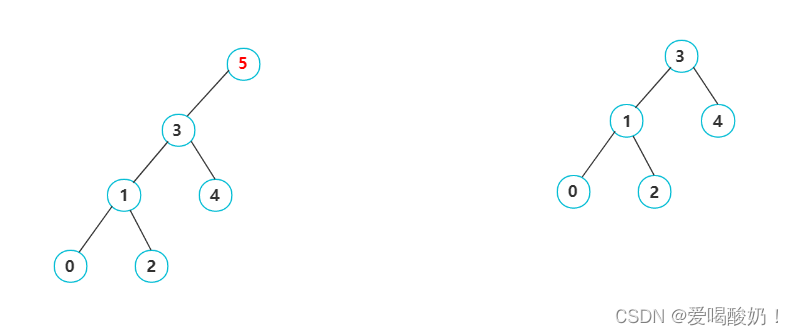
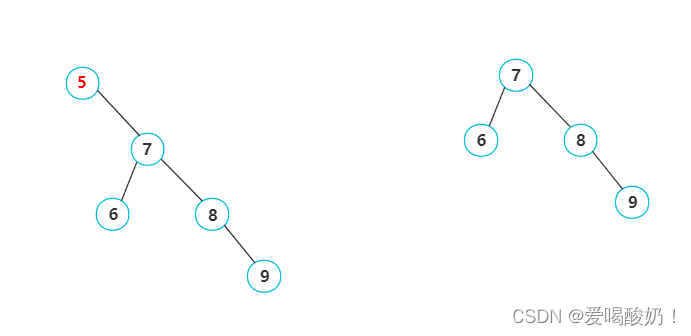
? ? [3]要删除的结点只有右孩子
? ? ? ? 如图,跟上个情况一样,让5结点的孩子结点当根结点,删除5结点即可。
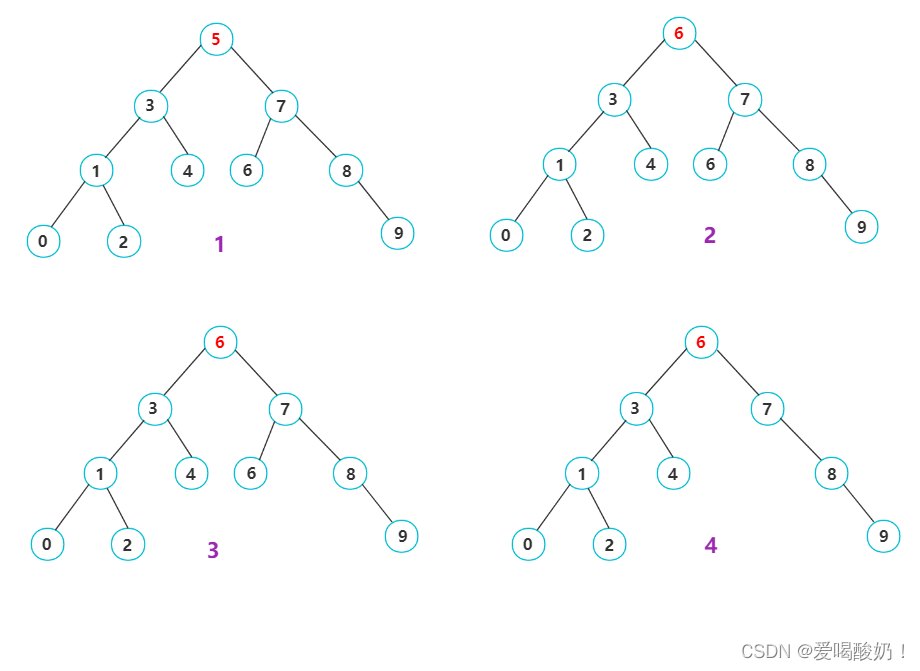
? ? [4]要删除的结点有左右两个孩子
? ? ? ? 这里采用的是找右子树最小结点。
? ? ? ? 如图:找到根结点右子树中最左侧的结点是6,用6替换根结点,此时根结点是红6,然后删除替代结点即可。
3.二叉搜索树实现
? ? ? ? 为了实现的方便,我们规定二叉树中的值是唯一的,没有重复的值。
? (1)二叉搜索树局部实现
? ? [1]二叉搜索树结点类
? ? ? ? 二叉搜索树中是用一个一个的结点存储数据的,因此我们需要单独为结点定义一个类。
? ? ? ? 因为结点中可能存储各种类型的的元素,因此结点类是模板。这个类中的成员变量:指向左右孩子的指针,存储元素的value变量。成员函数只需要一个构造函数即可,构造一个空的结点。
//二叉搜索树结点类
template<typename T>
struct BSTNode {
BSTNode<T>* left;//左孩子指针
BSTNode<T>* right;//右孩子指针
T value;//存储值
//构造函数
BSTNode(const T& _value = T())
:value(_value)
,left(nullptr)
,right(nullptr)
{}
};? ? [2]二叉搜索树成员变量
? ? ? ? 因为二叉搜索树是模板,所以不要忘记加上模板参数。同时用typedef关键字给结点类取一个别名,这样使用起来会方便很多。
? ? ? ? 二叉搜索树的成员变量只有一个,那就是指向根结点的指针。
//二叉搜索树类
template<typename T>
class BinarySearchTree {
//为结点类取别名
typedef BSTNode<T> Node;
private:
//根结点指针
Node* root;
};? ? [3]无参构造
? ? ? ? 因为用无参构造会构造空树,因此根结点需要指向空。
//无参构造
BinarySearchTree()
:root(nullptr)
{}
? ? [4]析构函数
? ? ? ? 因为析构函数没有参数,所以需要单独设置一个销毁函数。销毁函数的参数是根结点指针,通过递归调用销毁函数,首先销毁根结点的左右孩子,最后销毁根结点自身,不要忘记将根结点指针指向空。
//析构函数
~BinarySearchTree(){
//内部调用销毁函数
Destroy(root);
}
//销毁函数
void Destroy(Node*& root) {
if (root) {
//递归调用销毁函数对该结点的左子树和右子树进行销毁
Destroy(root->left);
Destroy(root->right);
//将该结点的左右子树销毁后销毁该结点自身
delete root;
root = nullptr;
}
}? ? [5]插入函数
? ? ? ? 插入函数的步骤在上面已经用图片展示过了,所以这里就不多赘述了,每个步骤的意义已经用注释写上了。
//插入函数
bool Insert(const T& _value) {
//要插入的是空树
if (root == nullptr) {
root = new Node(_value);
return true;
}
//要插入的不是空树
//parent保存cur的双亲
Node* cur = root;
Node* parent = nullptr;
//用循环结构查找适合_value的位置
while (cur) {
//用parent保存cur结点
parent = cur;
//cur的值小于_value,就去cur的右子树找
if (cur->value < _value) {
cur = cur->right;
}
//cur的值大于_value,就去cur的左子树找
else if (cur->value > _value) {
cur = cur->left;
}
//cur的值等于_value,说明树中存在该结点,返回false
else {
return false;
}
}
//能运行到这里,说明找到了合适的位置
// 此时cur指向空,parent是cur的双亲
//将_value元素放入cur中
cur = new Node(_value);
//判断_value应该存储到parent结点的左子树还是右子树
if (parent->value < _value) {
parent->right = cur;
}
else {
parent->left = cur;
}
//插入成功返回true
return true;
}
? ? [6]查找函数
? ? ? ? 查找函数也比较简单,根据上文的讲解结合注释也可以很轻松地理解。
//查找函数
Node* Find(const T& _value) {
//用cur保存根结点,因为是从根结点开始查找
Node* cur = root;
while (cur) {
//cur的值小于_value,说明_value如果存在,就一定在右子树中
if (cur->value < _value) {
cur = cur->right;
}
//cur的值大于_value,说明_value如果存在,就一定在左子树中
else if(cur->value > _value){
cur = cur->left;
}
//cur的值等于_value,说明恰好找到,返回cur
else {
return cur;
}
}
//循环体没有中途结束,说明整个树中都没找到
//返回空
return nullptr;
}
? ? [7]中序遍历函数
? ? ? ? 中序遍历不应该让用户传递指针参数,所以需要单独进行内部实现。中序遍历的遍历顺序:左、根、右。程序的设计也是根据这个顺序进行,首先递归遍历左子树,然后打印根结点,最后递归遍历右子树。
? ? ? ? 注意:如果读者用文末提供的代码进行测试就可以发现,中序遍历得到的结果是一个升序的序列。
//中序遍历函数
void InOrder() {
cout << "中序遍历" << endl;
InOrder(root);
cout << endl;
}
//中序遍历函数内部实现
void InOrder(Node* root) {
if(root){
//先遍历左子树
InOrder(root->left);
//再访问根结点
cout << root->value << " ";
//最后遍历右子树
InOrder(root->right);
}
}
? ? [8]删除函数
? ? ? ? 删除函数是一个难点,这里需要再详细说一说。
? ? ? ? 首先需要判断是否是空树,如果是空树,就返回false,因为空树没有元素,不能删除。如果树不空,需要在书中查找是否有需要删除的这个元素,如果没有返回false。
? ? ? ? 如果找到需要被删除的结点,cur就是被删除的结点。然后需要根据cur的孩子的情况进入不同的选择语句。
? ? ? ? 进入不同的选择语句后,需要根据cur是否有双亲的情况再次进入不同的选择语句。
? ? ? ? 二次进入选择语句后,再次判断cur是双亲的左孩子还是右孩子,进行不同的操作。
? ? ? ? 在上文中通过大量图片讲解了每一种情况的处理,希望可以结合图片一起看下面的代码,同时代码中也写了相应的注释。
//删除函数
bool Erase(const T& _value) {
//如果是空树直接返回false
if (root == nullptr) {
return false;
}
//parent用来保存cur的双亲
Node* cur = root;
Node* parent = nullptr;
//先查找对应结点
while (cur) {
if (cur->value == _value) {
break;
}
else if (cur->value > _value) {
parent = cur;
cur = cur->left;
}
else {
parent = cur;
cur = cur->right;
}
}
//节点不存在,直接返回false
if (cur == nullptr) {
return false;
}
//结点存在
//只有右孩子或者是叶子结点
if (cur->left == nullptr) {
//双亲结点是空,cur是根
//让cur的右孩子作为新的根结点
if (parent == nullptr) {
root = cur->right;
}
//cur有双亲,cur不是根
else {
//cur是叶子节点
//cur是parent的左孩子
//让parent的左孩子指针指向cur的右孩子
if(cur == parent->left){
parent->left = cur->right;
}
//cur是parent的右孩子
//让parent的右孩子指针指向cur的右孩子
else {
parent->right = cur->right;
}
}
}
//只有左孩子
else if (cur->right == nullptr) {
//cur是根
//让cur的左孩子作为新的根结点
if (parent == nullptr) {
root = cur->left;
}
//cur不是根
else {
//cur是parent的左孩子
//让parent的左孩子指针指向cur的右孩子
if (cur == parent->left) {
parent->left = cur->left;
}
//cur是parent的右孩子
//让parent的右孩子指针指向cur的右孩子
else {
parent->right = cur->left;
}
}
}
//cur有两个孩子
else {
//假设在右子树找替代节点
//delNode保存cur的右子树的根结点
Node* delNode = cur->right;
//parnet保存delNode的双亲
parent = cur;
//只要delNode还有左孩子就一直循环
//当delNode没有左孩子了
//那么它的双亲结点parent就是最左侧的结点了
while (delNode->left) {
parent = delNode;
delNode = delNode->left;
}
//把替代节点中的值赋值给被删除节点
cur->value = delNode->value;
//替代结点如果是parent的左孩子
//就让parent的左孩子指针指向替代节点的右孩子
//因为替代节点虽然没有左孩子
//但可能有右孩子
if (delNode == parent->left) {
parent->left = delNode->right;
}
else {
parent->right = delNode->right;
}
//用cur指向替代节点
cur = delNode;
}
//删除替代结点
delete cur;
//结点删除成功,返回true
return true;
}
? (2)二叉搜索树整体实现
#include "iostream"
using namespace std;
//二叉搜索树结点类
template<typename T>
struct BSTNode {
BSTNode<T>* left;//左孩子指针
BSTNode<T>* right;//右孩子指针
T value;//存储值
//构造函数
BSTNode(const T& _value = T())
:value(_value)
,left(nullptr)
,right(nullptr)
{}
};
//二叉搜索树类
template<typename T>
class BinarySearchTree {
//为结点类取别名
typedef BSTNode<T> Node;
private:
//根结点指针
Node* root;
public:
//无参构造
BinarySearchTree()
:root(nullptr)
{}
//析构函数
~BinarySearchTree(){
//内部调用销毁函数
Destroy(root);
}
//销毁函数
void Destroy(Node*& root) {
if (root) {
//递归调用销毁函数对该结点的左子树和右子树进行销毁
Destroy(root->left);
Destroy(root->right);
//将该结点的左右子树销毁后销毁该结点自身
delete root;
root = nullptr;
}
}
//插入函数
bool Insert(const T& _value) {
//要插入的是空树
if (root == nullptr) {
root = new Node(_value);
return true;
}
//要插入的不是空树
//parent保存cur的双亲
Node* cur = root;
Node* parent = nullptr;
//用循环结构查找适合_value的位置
while (cur) {
//用parent保存cur结点
parent = cur;
//cur的值小于_value,就去cur的右子树找
if (cur->value < _value) {
cur = cur->right;
}
//cur的值大于_value,就去cur的左子树找
else if (cur->value > _value) {
cur = cur->left;
}
//cur的值等于_value,说明树中存在该结点,返回false
else {
return false;
}
}
//能运行到这里,说明找到了合适的位置
// 此时cur指向空,parent是cur的双亲
//将_value元素放入cur中
cur = new Node(_value);
//判断_value应该存储到parent结点的左子树还是右子树
if (parent->value < _value) {
parent->right = cur;
}
else {
parent->left = cur;
}
//插入成功返回true
return true;
}
//查找函数
Node* Find(const T& _value) {
//用cur保存根结点,因为是从根结点开始查找
Node* cur = root;
while (cur) {
//cur的值小于_value,说明_value如果存在,就一定在右子树中
if (cur->value < _value) {
cur = cur->right;
}
//cur的值大于_value,说明_value如果存在,就一定在左子树中
else if(cur->value > _value){
cur = cur->left;
}
//cur的值等于_value,说明恰好找到,返回cur
else {
return cur;
}
}
//循环体没有中途结束,说明整个树中都没找到
//返回空
return nullptr;
}
//中序遍历函数
void InOrder() {
cout << "中序遍历" << endl;
InOrder(root);
cout << endl;
}
//中序遍历函数内部实现
void InOrder(Node* root) {
if(root){
//先遍历左子树
InOrder(root->left);
//再访问根结点
cout << root->value << " ";
//最后遍历右子树
InOrder(root->right);
}
}
//删除函数
bool Erase(const T& _value) {
//如果是空树直接返回false
if (root == nullptr) {
return false;
}
//parent用来保存cur的双亲
Node* cur = root;
Node* parent = nullptr;
//先查找对应结点
while (cur) {
if (cur->value == _value) {
break;
}
else if (cur->value > _value) {
parent = cur;
cur = cur->left;
}
else {
parent = cur;
cur = cur->right;
}
}
//节点不存在,直接返回false
if (cur == nullptr) {
return false;
}
//结点存在
//只有右孩子或者是叶子结点
if (cur->left == nullptr) {
//双亲结点是空,cur是根
//让cur的右孩子作为新的根结点
if (parent == nullptr) {
root = cur->right;
}
//cur有双亲,cur不是根
else {
//cur是叶子节点
//cur是parent的左孩子
//让parent的左孩子指针指向cur的右孩子
if(cur == parent->left){
parent->left = cur->right;
}
//cur是parent的右孩子
//让parent的右孩子指针指向cur的右孩子
else {
parent->right = cur->right;
}
}
}
//只有左孩子
else if (cur->right == nullptr) {
//cur是根
//让cur的左孩子作为新的根结点
if (parent == nullptr) {
root = cur->left;
}
//cur不是根
else {
//cur是parent的左孩子
//让parent的左孩子指针指向cur的右孩子
if (cur == parent->left) {
parent->left = cur->left;
}
//cur是parent的右孩子
//让parent的右孩子指针指向cur的右孩子
else {
parent->right = cur->left;
}
}
}
//cur有两个孩子
else {
//假设在右子树找替代节点
//delNode保存cur的右子树的根结点
Node* delNode = cur->right;
//parnet保存delNode的双亲
parent = cur;
//只要delNode还有左孩子就一直循环
//当delNode没有左孩子了
//那么它的双亲结点parent就是最左侧的结点了
while (delNode->left) {
parent = delNode;
delNode = delNode->left;
}
//把替代节点中的值赋值给被删除节点
cur->value = delNode->value;
//替代结点如果是parent的左孩子
//就让parent的左孩子指针指向替代节点的右孩子
//因为替代节点虽然没有左孩子
//但可能有右孩子
if (delNode == parent->left) {
parent->left = delNode->right;
}
else {
parent->right = delNode->right;
}
//用cur指向替代节点
cur = delNode;
}
//删除替代结点
delete cur;
//结点删除成功,返回true
return true;
}
};
int main(){
BinarySearchTree<int> bt;
int arr[] = {6,7,8,9,2,3,0,1,4,5};
int size = 10;
int i = 0;
while (size) {
bt.Insert(arr[i]);
i++;
size--;
}
bt.Erase(6);
bt.Erase(3);
bt.InOrder();
}
?
?