题目

题目连接

给定一个 m x n 整数矩阵 matrix ，找出其中最长递增路径的长度。

对于每个单元格，你可以往上，下，左，右四个方向移动。你不能在对角线方向上移动或移动到边界外（即不允许环绕）。

示例 1：

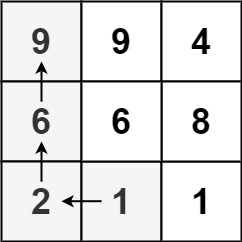
在这里插入图片描述

输入：matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出：4

解释：最长递增路径为 [1, 2, 6, 9]。
示例 2：

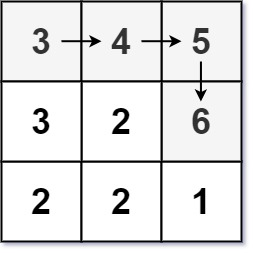
在这里插入图片描述

输入：matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出：4

解释：最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。
示例 3：

输入：matrix = [[1]]
输出：1

解题

方法一：记忆化dfs

正常思路下，遍历每个点，然后朝四个方向dfs，由于只会朝着递增的方向dfs，因此不用关注再次遍历已经访问过的点，但是这种方式会超时。
因此进行了记忆化，对于每个点，dp[i][j]表示，在位置i,j上为起点的最长递增路径
初始化dp[i][j]=1，因为每个点最短递增路径就是1，就是仅包含自身。

如果dp[i][j]不为1了，说明已经更新了该点，直接使用就行了。会出现还没更新完dp[i][j]，就去访问该点的情况吗？是不会的，因为如果dp[i][j]还没更新完，那么也就是此时说在查找比matrix[i][j]更大的点，不可能访问matrix[i][j]。因此出现dp[i][j]不为1的情况，直接用就行了

class Solution {
public:
    int m,n;
    vector<vector<int>> dirs={{-1,0},{0,-1},{1,0},{0,1}};
    void dfs(vector<vector<int>>& matrix,vector<vector<int>>& dp,int x,int y){
        for(vector<int>& dir:dirs){
            int nx=x+dir[0];
            int ny=y+dir[1];
            if(nx<0||nx>=m||ny<0||ny>=n||matrix[nx][ny]<=matrix[x][y]) continue;
            if(dp[nx][ny]==1) dfs(matrix,dp,nx,ny);
            dp[x][y]=max(dp[x][y],dp[nx][ny]+1);
        }

    }
    int longestIncreasingPath(vector<vector<int>>& matrix) {
        m=matrix.size(),n=matrix[0].size();
        vector<vector<int>> dp(m,vector<int>(n,1));
        int res=0;
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(dp[i][j]!=1) continue;
                dfs(matrix,dp,i,j);
                res=max(res,dp[i][j]);
            }
        }
        return res;
    }
};

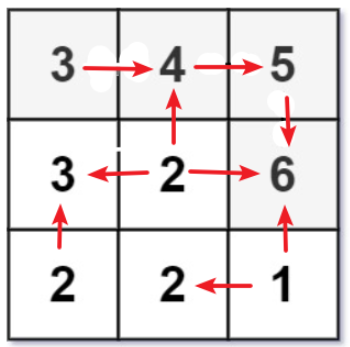
方法二：拓扑排序

将矩阵转化成一张拓扑图
进行多源的拓扑排序
拓扑排序的深度，就是最长的递增路径
在这里插入图片描述
参考链接

class Solution {
public:
    int m,n;
    vector<vector<int>> dirs={{-1,0},{0,-1},{1,0},{0,1}};
    int longestIncreasingPath(vector<vector<int>>& matrix) {
        m=matrix.size(),n=matrix[0].size();
        //计算入度
        vector<vector<int>> indeg(m,vector<int>(n,0));
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                for(vector<int>& dir:dirs){
                    int nx=i+dir[0],ny=j+dir[1];
                    if(nx<0||nx>=m||ny<0||ny>=n||matrix[nx][ny]<=matrix[i][j]) continue;
                    indeg[nx][ny]++;
                }
            }
        }

        //拓扑排序
        queue<pair<int,int>> q;
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(indeg[i][j]==0){
                    q.push({i,j});
                }
            }
        }
        int res=0;
        while(!q.empty()){
            res++;
            int l=q.size();
            while(l--){
                auto [x,y]=q.front();
                q.pop();
                for(vector<int>& dir:dirs){
                    int nx=x+dir[0],ny=y+dir[1];
                    if(nx<0||nx>=m||ny<0||ny>=n||matrix[nx][ny]<=matrix[x][y]) continue;//这样子就可以不用浪费额外空间建图
                    if(--indeg[nx][ny]==0) q.push({nx,ny});
                }
            }
        }
        return res;

    }
};