树的定义
树的结构
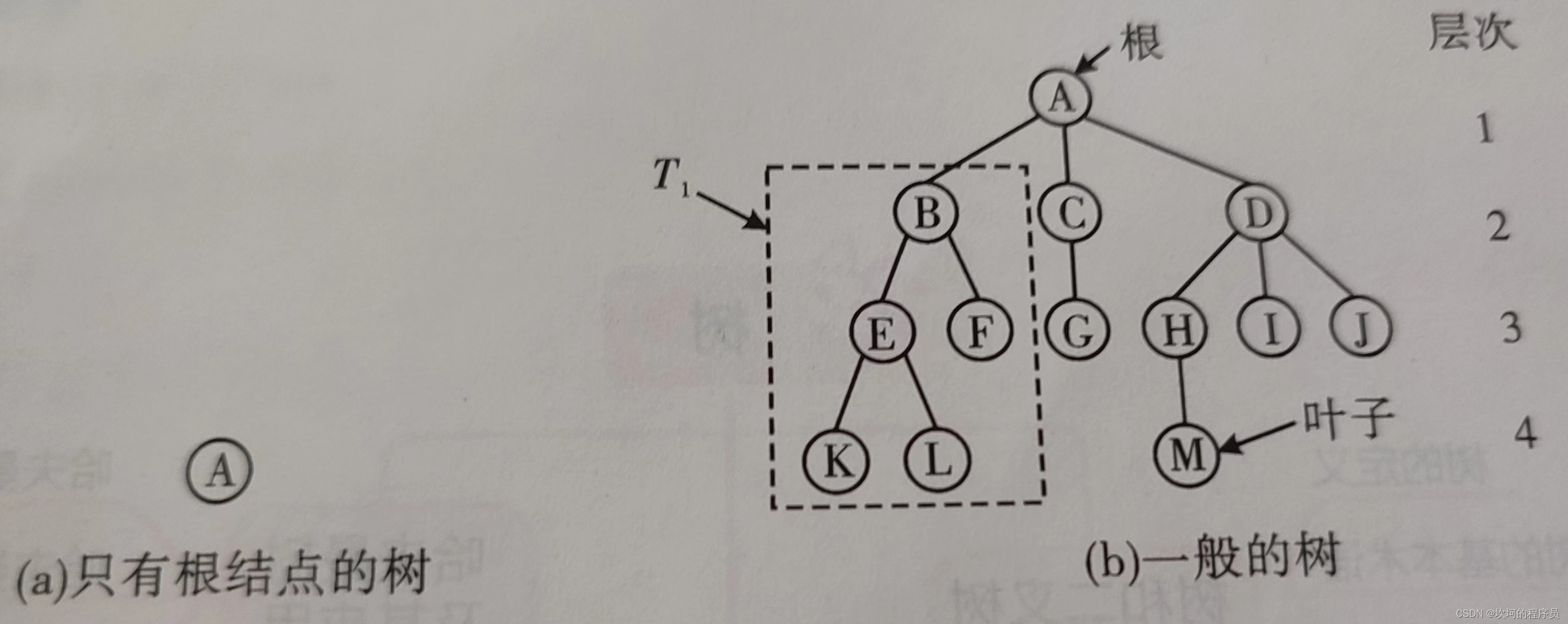
1.树的结点：A,B,C就是这些就是结点。
2.结点的度：某个结点所拥有的子树就是他的度，B的度就是1，A是3。
3.树的度：结点度最大的，就是树的度。
4.叶子：度为0的结点就是叶子或者终端结点，例如K,L结点。
5.非终端结点：度不为0的结点，也可以称为内部结点。
6.双亲：就是父结点，B的双亲就是A。
7.孩子:子结点，B的孩子就是E,F。
8.兄弟：同一个双亲的孩子。
9.祖先:一个结点所从自身向上经过的结点都是祖先，E的祖先就是A，B。
10.子孙：以某个结点为根的子树下的所有结点都是子孙，例如：E,F,K,L都是B的子孙。
11.层次：就是树有多少层，上图有4个层次。
12.堂兄弟：双亲在同一层的结点，E,F,G,H,I,J都是堂兄弟。
13.树的深度:树最大的层数。
14.有序树和无序树：按照从左到右的次序（不能更换次序），称为有序树，否则就是无序树。
15.森林：子树的集合就是树
二叉树的定义
1.没有结点就是空树。
2.非空的条件：只有一个根节点的，拥有左子树和右子树，其子树也是二叉树。
二叉树的分类
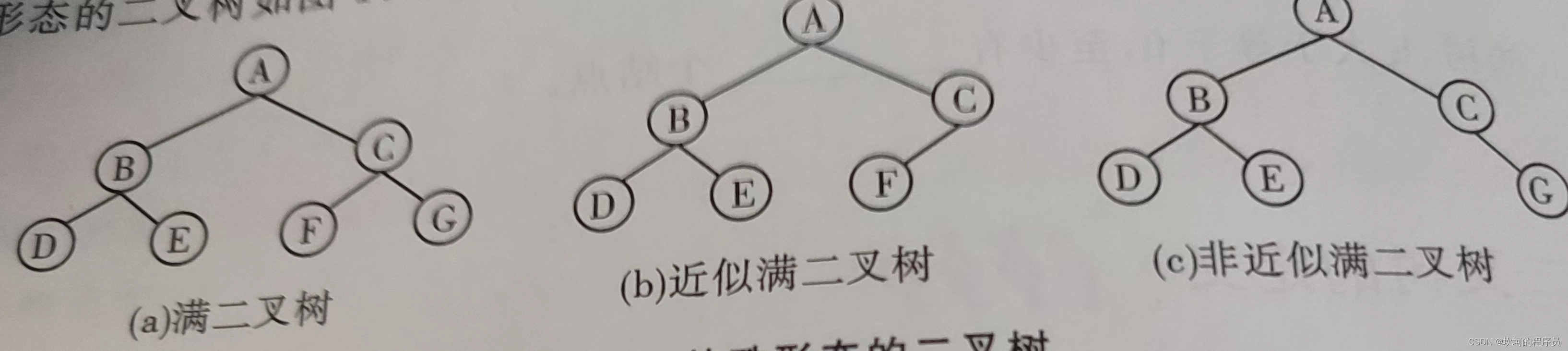
1.满二叉树：
深度为k二叉树的结点一共有**(2^k)-1个结点，深度3，结点一共有：7.**
每一层的节点数都具有2^i-1,第三层，结点最多有4个。
每个结点不存在度为1。
2.完全二叉树：
1.和二叉树有一样的次序。
2.只有最后两层的结点的度可以小于2.
3.右分支下的层数最大为L,左分支下的子孙一定为L或L+1
二叉树的性质
第i层上，最多右2^i-1个结点，第2层，最多2个结点。
深度为k的二叉树最多右(2^k)-1个结点，深度3，最多7个结点。
叶子结点数为n0，度为2的结点数为2，n0 = n2-1，叶子结点的总和 = 度为2的结点+1
二叉树的存储结构
顺序存储
从左到右编号
一般二叉树的顺序结构，对于缺少的数据，可以用？来替代
链式存储
链表中有数据域和左右指针域 --二叉链表。
链表中除了上述所说的3个指针，还可以添加指向双亲的指针–三叉链表。
树的表示方法
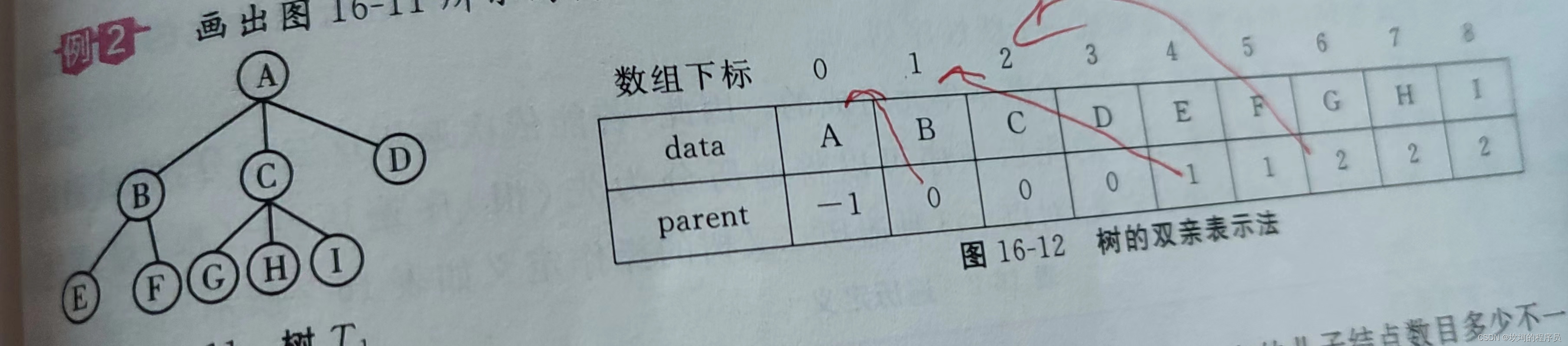
双亲表示法
a没有双亲，所有parent-1，parent除了最大的根节点，其他孩子都是根据自己的双亲编号填入的，比如B所在的双亲编号是0，那parent就填0
孩子表示法
孩子表示法：首先找出子树下有孩子的根结点，然后指针就指向对应的孩子的编号。
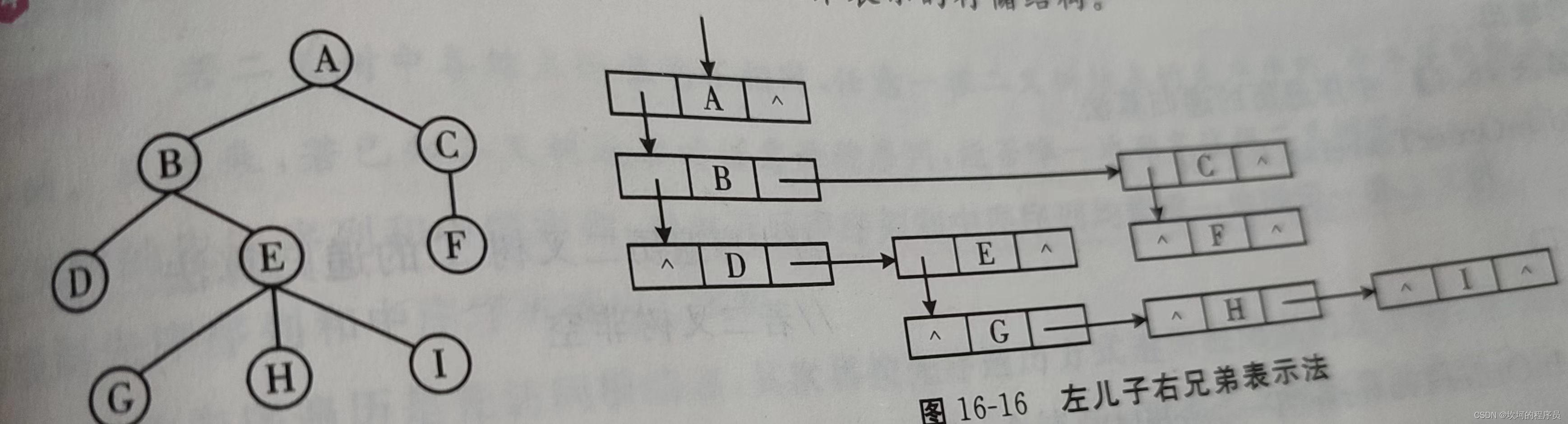
孩子兄弟表示
通过孩子结点和兄弟结点来表示
例如：A下面B长子,B有堂兄弟C，然后B下面有孩子D。
遍历二叉树
先序遍历
从根结点开始，然后先去左子树，最后右子树。
中序遍历
从左子树的底开始（从左到右），然后到根结点，然后再从右子树的底向上遍历（从左到右）（不经过根节点）
后序遍历
先从左到右遍历左子树（不去根节点），然后去右子树（从左到右遍历），最后到根结点。
线索二叉树
这种结构构成的二叉链表作为二叉树的存储结构，叫做线索链表。
前驱和后继指针叫做线索。
加上线索的二叉树叫做线索二叉树。
对二叉树以某种次序遍历使其变为线索二叉树的过程叫做线索化。
树和森林,二叉树转化
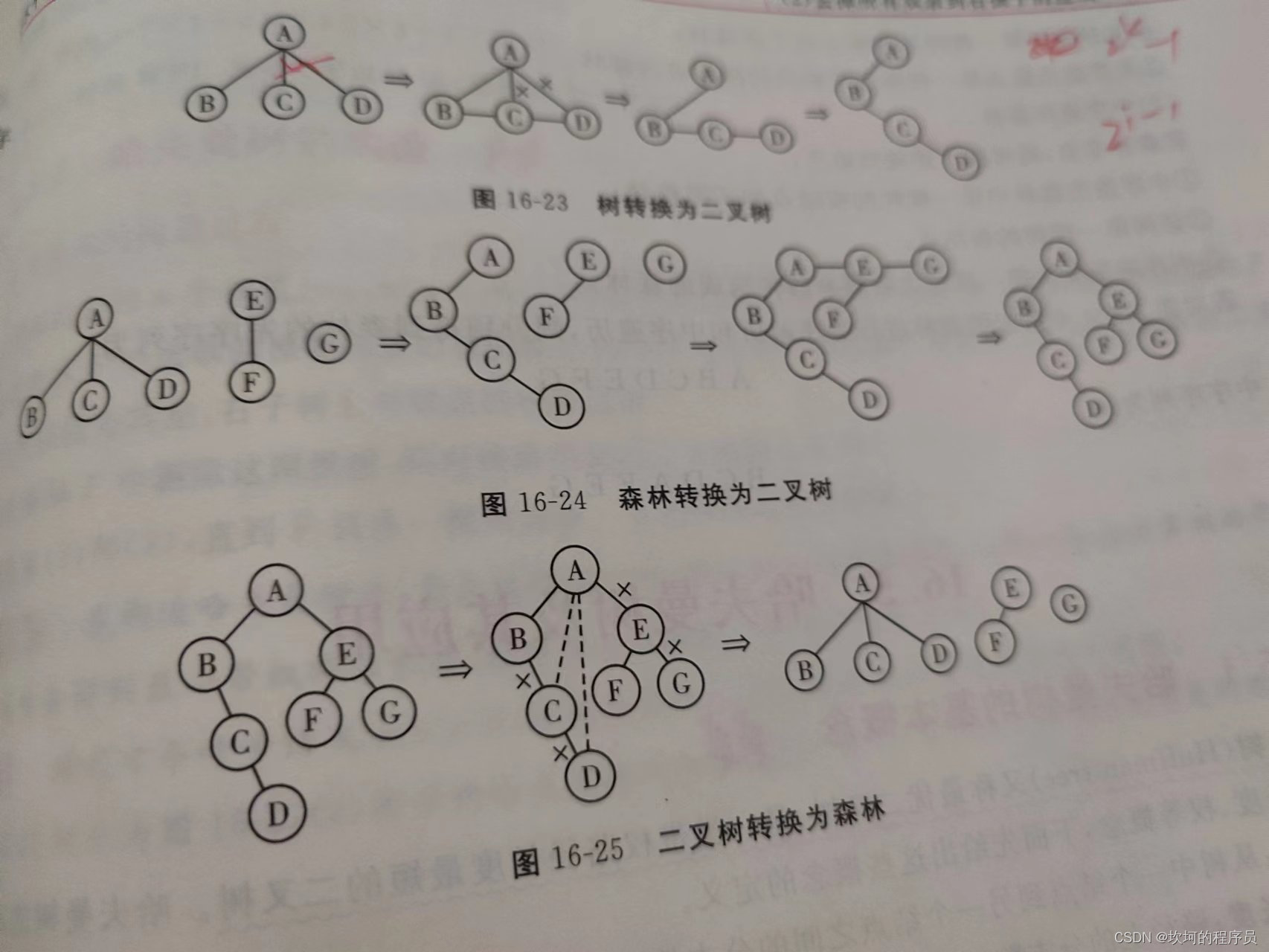
树转化为二叉树：就是将除了长子之外的兄弟结点都砍掉，放到长子下面。
森林转化为二叉树：就是将根节点连起来。
二叉树转化为森林：把兄弟结点连回来，将根节点A下面的线拉直，A和E和G，都是森林的根节点。
树的遍历和森林的遍历
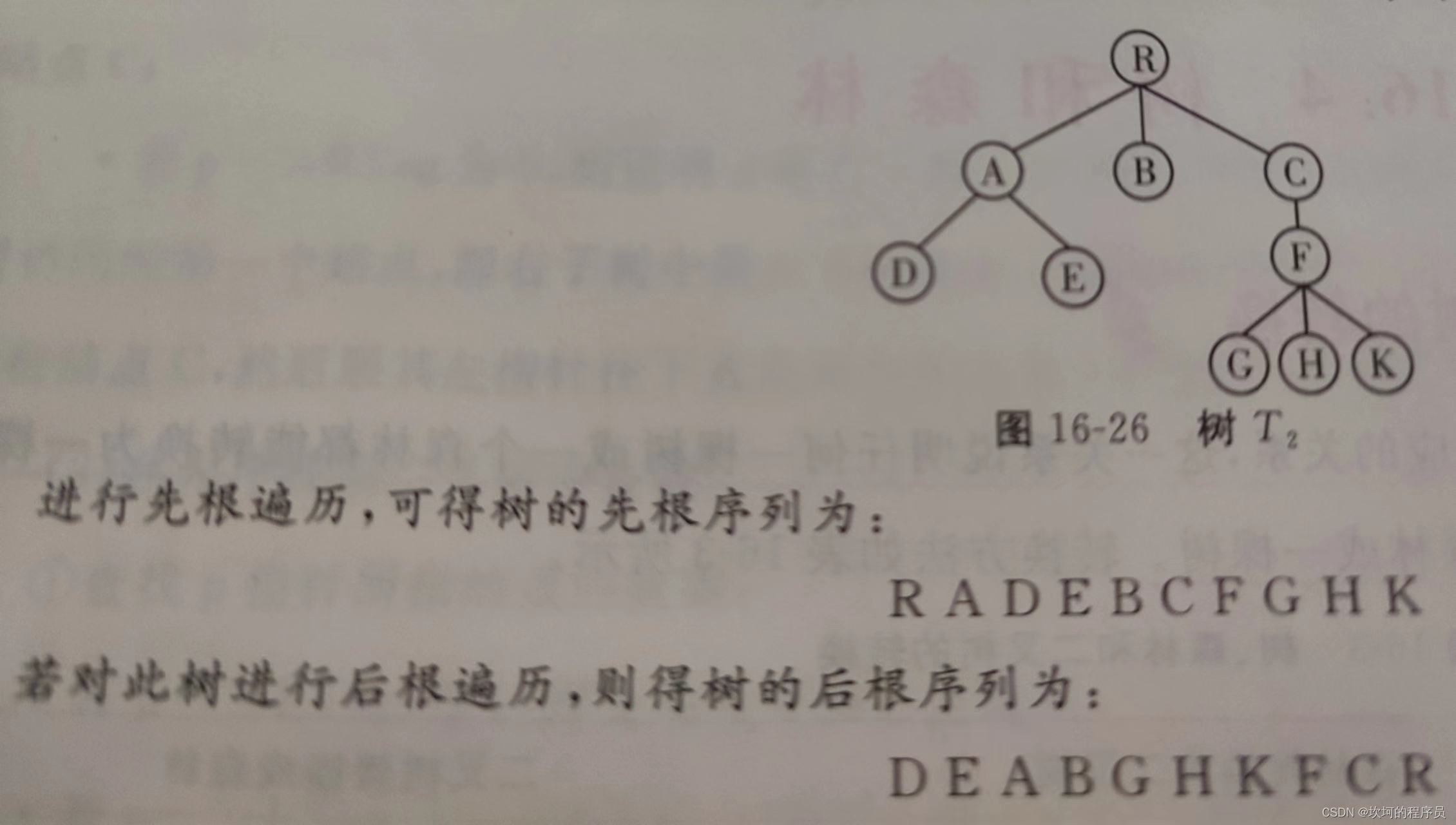
树的遍历
先跟遍历，从根节点开始，从左子树-右子树的遍历
从左子树左边开始遍历，一个一个的遍历，最后再到根节点R。
森林的遍历
先序遍历：一颗树一颗树的从上往下遍历（A,B,C,D,E,F,G）
后序遍历，一颗一颗树的从后往上遍历(B,C,D,A,F,E,G)
哈夫曼树
哈夫曼树是最优二叉树，路径最短的二叉树。
路径：一个结点到根节点的分支叫路径
路径长度，经过几个分支，就是多少长度。
权：就是给结点的量
结点带权路径的长度：权*路径
树的带权路径长度：所有叶子结点带权路径的长度总和。
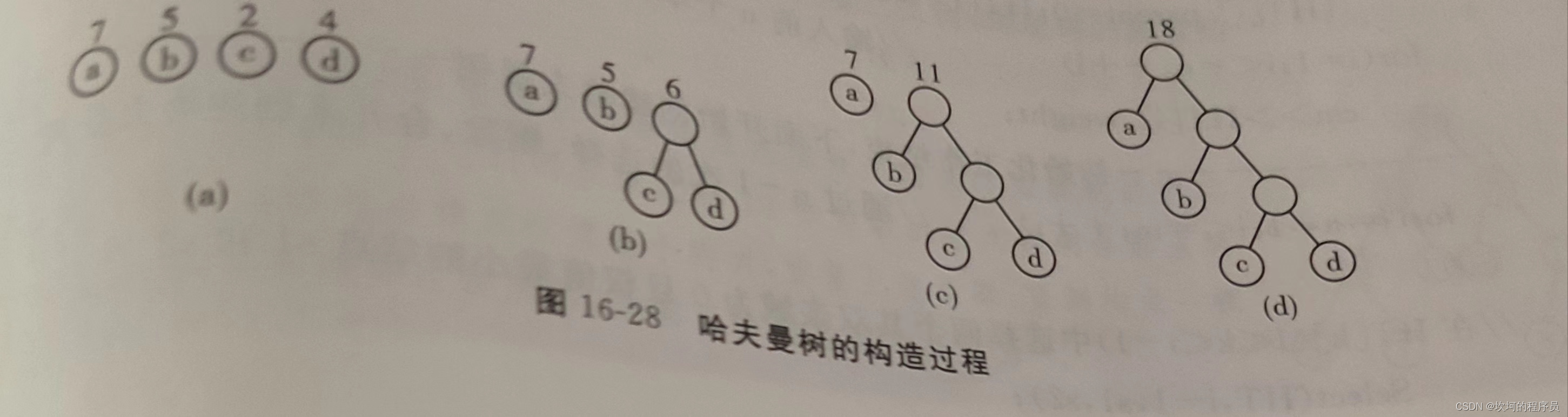
哈夫曼树的构造
权小的放在左边，权大的放在右边 （c在左，d在右），然后c和d形成一棵树
然后把b放在左边，形成一棵树
最后还有一个a，放在左边，形成一棵树
二叉排序树
左不空，左比根结点的值小，右比根节点大（插入的时候也是这样判断的）
平衡二叉树
左子树和右子树的深度只差绝对值不超过1