今天继续学习算法,这节课主要是查找算法,最主要的是哈希算法,其他例如二叉搜索树,二叉平衡树都已经在数据结构专栏接触过了,所以这节课主要讲述哈希算法。
文章目录
1.基础哈希
(1)直接映射表的定义
- 假设有一些键来自一个有m个元素的集合U,假定这些键是相互独立的
- 当你建立一个从0到m-1的数组T[0,m-1]来表示动态集合S
- 当x属于S且其键值为k,那么那么x对应的值就是T[k]
- x不属于S,则对应的值不存在
- 所有的时间复杂度,即使是最坏的情况也是O(1)
(2)直接映射表的缺点与改进
- 当我们存储字符串时,需要更多的空间,且大部分空间会浪费
- 不能直接查找最大值,最小值
- 我们针对第一个问题进行修改——哈希表
(3)哈希表的定义
- 用一个哈希函数H来“随机”(并不是完全的随机)映射,把键映射到哈希表T的槽位(数组的索引)
- 我们建立一个很大的键的全域,称之为U
- 我们再建立一个有m个槽位的哈希表
- 在全域里有一个集合S,从S取一个键映射到哈希表里
- 当然会发生一种情况:
当键映射时,已经有一个键被赋予了一样的值,导致指向了一个槽位,我们称这种现象为碰撞。
- 哈希表的优化有两种方法:
链表法和开放寻址法
- 其理想情况是真正的随机分布,将键值基本随机映射到一个槽上,称其为简单均匀哈希
(4)哈希表的优化——链表法
- 分析:
把相同的哈希值的记录放入一个链表里储存 - 最坏情况分析:
所有的键都映射到同一个槽位,访问需要Θ(N).
定义一个存放n个键,有m个槽的哈希表,它的转载因子α=n/m,每个槽里的平均键的数量
- 平均情况分析:
当搜索失败时,其期望的时间复杂度为:Θ(1+α);当n=O(m)或者α=O(1)时,其期望的时间复杂度为Θ(1);当搜索成功时,其期望的时间复杂度也为:Θ(1+α) - 平均情况的分析是建立在简单均匀哈希上的
(5)如何选择哈希函数
- 把键均匀的分布在槽里
- 键本身也具有一些分布的特性,不会影响它在哈希表中而非内部的均匀性
例如:
除法哈希算法:
- 所有插入的键值都是偶数,并且我的哈希函数是一个偶数取余,那么我的奇数槽位就浪费了
- 在二进制中,对2^r取余,就是看它最后r位数
乘法哈希算法:
- 假定计算机的一个字的长度为w位(比如32位或者64位)
- 假设哈希表长度m=2^r,且m都是整数
- A和k是两个常数,且为w位
- 公式:h(k)=(A * k mod 2^w)rsh(w-r)
- A是一个奇数,大于2^(w-r),小于2^w,rsh是“按位右移”运算符
- 不要选太接近2^w或者2^(w-1)
- A?k在二进制下长度为2 w位,两个w位的二进制数相乘得到的是2w位的二进制数
(5)哈希表的优化——开放寻址法
- 在这个方法中,我们不需要链表
- 我们不想用额外的内存开支(链表的节点),也不想对记录做改动,这种情况下用开放寻址法
- 系统的探查哈希表,直到找到一空的槽位
- h:U{0,1,…,m-1}->{0,1,…,m-1}
- 探查序列是一个算数排列
- 搜索也是用同样的探查序列,成功返回相应的记录,失败返回NULL
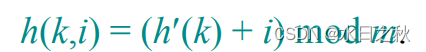
有不同的探查方法:
- 线性探查方法:
其中h'(k)是普通的散列函数
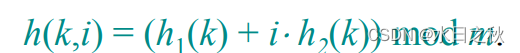
- 二次哈希:
这是最受欢迎的哈希函数
h1(k)和h2(k)都是哈希函数
通常m取2,h2(k)为奇数
- 平均情况分析:假设一个均匀哈希(每一个键都分布均匀,都可能是m!种探查序列任何一种),每个键相互独立,当α<1时,其期望探查次数最多不超过1/(1-α)
这意味着:
- 如果α是常数,那么访问哈希表的时间为常数时间
- 如果表是半满的,预期的探测数为1/(1-0.5)=2
- 如果表是90%满的,预期的探测数为1/(1-0.9)=10
证明:
- 第一次探测发生碰撞的概率为n/m
- 第二次探测发生碰撞的概率为(n-1)/(m-1)
- 第k次探测发生碰撞的概率为(n-k+1)/(m-k+1)
- 所以(n-k)/(m-k)<n/m<α
- 那么预期的探测数为:

2.全域哈希
哈希函数的缺点:对于任何哈希而言,都存在一个不好的键集,所有键集都会映射到同一个槽。
所以这里对哈希函数做优化——随机选择一个哈希函数,这样就会与键产生相对的独立。
(1)全域哈希的定义
- 设U为键的全域,H是哈希函数的有限集,H的哈希函数将U映射到哈希表的槽里——{0,1,…,m-1}。
- 如果满足所有的键对,键与键两两互异,那么就能满足下面的推论:
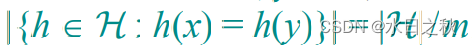
- 如果h是从全域H中选择,那么x与y发生碰撞的概率为1/m.
证明:
- 从哈希函数中选择到h的概率为1/|H|
- h的数量为|H|/m
- 所以x与y发生碰撞的概率为1/m.
(2)定理
- 随机的选择函数h
- 假设n个键放置到T表的m个槽里
- 对于给定的键x,它发生的碰撞的期望次数小于n/m.
证明:
- 设C_x为一个随机变量,它表示哈希表T的键与x发生的碰撞次数为发生碰撞的总次数。
- 当h(x)=h(y)时,c_xy=1,否则c_xy=0。
- 假设有一个进程在随机选择哈希函数,那么c_xy的期望为:1/m.
- C_x=sum(c_xy).
- 那么C_x的期望如下图
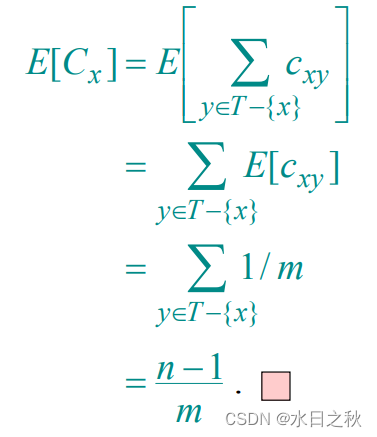
(3)构建一个哈希函数
- m是质数
- 将键k用r+1位表示,k=<k0,k1,…,kr>,其中0<=ki<=m-1
- 随机选择一个数a,a的每个位置都在0到m-1内
- 这里的a与r是用m进制数表示,而m的值正是槽的数量
- 则公式如下:
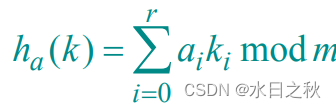
- 这样哈希函数集的大小为|H|=m^(r+1)
(4)点积哈希函数的普适性
定理:H是通用的
证明
- 设x = <x0,x1,…,xr>
- 设y = <y0,y1,…,yr>
- x与y是两个互异的键,这样r位的表达式在某一个位置是不同的。
- wlog(without loss of gererality,不丢失一般性)位置0——选择第零位
- 一定有一个哈希函数使得x与y 发生碰撞,那么可以推出:
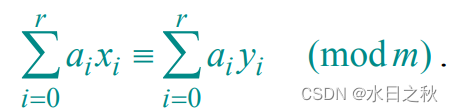
- 将式子做一些简单的变换,如下式:
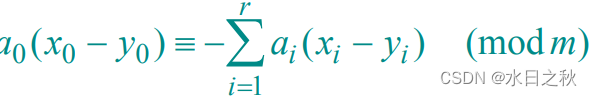
- 接下来需要一个定理才能继续进行
- 前提说明:以下这个定理只在m位质数时成立。
定理:
- 设z属于Z(z<m-1),且z!=0,其中Z是对m取余后的整数,总存在一个数z'属于Z,使得z * z'=1(mod m).(这里用z'代表z的倒数)
举例:

- 当z=3时,若要z * z' % 7 =1,则z'=5
- 通过观察发现,当z=5时,z'=3;当z=3时,z'=5. 所以z与z'互为倒数。
- 这样就能得到下式:
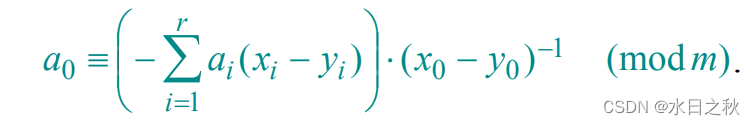
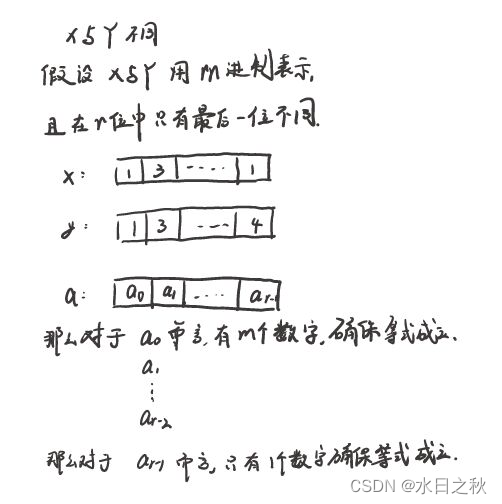
- 因此,每一个a_i的选择都会影响最终的a0
- 换句话说,如果确定了a_i(例如:a_1,a_2,...,a_r)那么最终的a0也是确定的,只有a0是这个特定的值,这时x与y才会碰撞,除此以外,其他a_i的选择则不会导致x与y碰撞
- 合计x与y碰撞的哈希函数的数量为m^r,也就是|H|/m
或许有点抽象,我自制一张表出来:
(4)完全哈希
- 给定n个键,创建一个静态的哈希表,表的大小为 m = O(n),使得在最坏的情况下,查找的时间为O(1)
- 其关键是双级结构,并且每一级都是使用全域哈希
- 这样键可以在第一级碰撞,但是在第二级不会发生碰撞
好了,以上就是本节课的主要内容,代码部分可以先根据本文内容自己尝试,之后再去寻找答案。