目录
方法介绍
动态规划(英语:Dynamic programming,简称 DP)是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
动态规划不是某一种具体的算法,而是一种算法思想:若要解一个给定问题,我们需要解其不同部分(即子问题),再根据子问题的解以得出原问题的解。与分治法不同,其分解得到的子问题往往是相互联系的。
动态规划常常适用于有重叠子问题和最优子结构性质的问题,并且记录所有子问题的结果,因此动态规划方法所耗时间往往远少于朴素解法。
动态规划有自底向上和自顶向下两种解决问题的方式。
①自顶向下即记忆化递归;
②自底向上就是递推。
使用动态规划解决的问题有个明显的特点,一旦一个子问题的求解得到结果,以后的计算过程就不会修改它,这样的特点叫做无后效性,求解问题的过程形成了一张有向无环图。动态规划只解决每个子问题一次,具有天然剪枝的功能,从而减少计算量。
动态规划算法适用于解最优化问题,其求解三大步骤:
①定义数组dp[i]中元素含义;
②找出数组元素之间的关系式;
③找出初始值;
练习题目
1、53.最大子序组和
题目(中等):给你一个整数数组?nums?,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组?是数组中的一个连续部分。
示例 1:输入:nums = [-2,1,-3,4,-1,2,1,-5,4]? 输出:6
解释:连续子数组?[4,-1,2,1] 的和最大,为?6 。
示例 2:输入:nums = [1]? 输出:1
示例 3:输入:nums = [5,4,-1,7,8]? 输出:23
求解:
关键理解:
我们?不知道和最大的连续子数组一定会选哪一个数,那么我们可以求出?所有?经过输入数组的某一个数的连续子数组的最大和。将问题分解为以下子问题:
子问题 1:以 -2?结尾的连续子数组的最大和是多少;
子问题 2:以 1?结尾的连续子数组的最大和是多少;
子问题 3:以 -3?结尾的连续子数组的最大和是多少;
...
其中子问题1以 -2?结尾的连续子数组是 [-2],因此最大和就是 ?2。
子问题 2:以 11 结尾的连续子数组的最大和是多少;
以 11 结尾的连续子数组有 [-2,1] 和 [1] ,其中 [-2,1] 就是在「子问题 1」的后面加上 1 得到。-2 + 1 = -1 < 1?2+1=?1<1 ,因此「子问题 2」 的答案是 11。
如果编号为 i 的子问题的结果是负数或者 0 ,那么编号为 i + 1 的子问题就可以把编号为 i 的子问题的结果舍弃掉(这里 i 为整数,最小值为 1 ,最大值为 8),这是因为:
一个数 a 加上负数的结果比 a 更小;
一个数 a 加上 0 的结果不会比 a 更大;
而子问题的定义必须以一个数结尾,因此如果子问题 i 的结果是负数或者 00,那么子问题 i + 1 的答案就是以 nums[i] 结尾的那个数。
复杂度分析
时间复杂度:O(n),其中 n?为nums 数组的长度。我们只需要遍历一遍数组即可求得答案。
空间复杂度:O(1),我们只需要常数空间存放若干变量。
代码1:
class Solution {
public int maxSubArray(int[] nums) {
int len=nums.length;
if(len==1){return nums[0];}
int[] dp=new int[len];//表示以nums[i]结尾的连续子数组的最大和
dp[0]=nums[0];
for(int i=1;i<len;i++){
if(dp[i-1]>0){
//连续子数组
dp[i]=dp[i-1]+nums[i];
}else{
//前一个结尾的最大连续数组和为负,则舍弃重新开始
dp[i]=nums[i];
}
}
int res=nums[0];
for(int i=0;i<len;i++){
//遍历dp数组,找到最大和
res=Math.max(res,dp[i]);
}
return res;
}
}代码2:
class Solution {
public int maxSubArray(int[] nums) {
int len=nums.length;
if(len==1){return nums[0];}
int res=nums[0];
int pre=0;
for(int num:nums){
pre=Math.max(num,pre+num);
res=Math.max(pre,res);
}
return res;
}
}2、124.二叉树的最大路径和
题目(困难):路径被定义为一条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
示例 1:
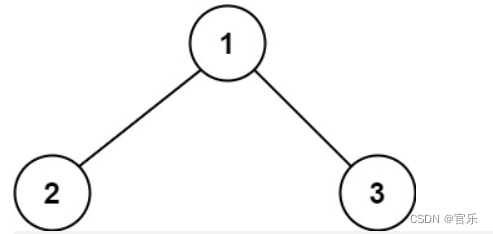
输入:root = [1,2,3]
输出:6
解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
示例 2:
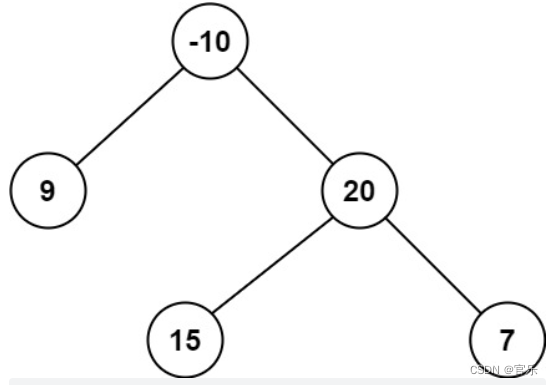
输入:root = [-10,9,20,null,null,15,7]
输出:42
解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
?求解:
考虑实现一个简化的函数 maxGain(node),该函数计算二叉树中的一个节点的最大贡献值,具体而言,就是在以该节点为根节点的子树中寻找以该节点为起点的一条路径,使得该路径上的节点值之和最大。
具体而言,该函数的计算如下。
·空节点的最大贡献值等于 0。
·非空节点的最大贡献值等于节点值与其子节点中的最大贡献值之和(对于叶节点而言,最大贡献值等于节点值)。
例如:
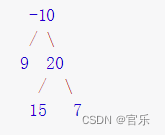
叶节点 9、15、7?的最大贡献值分别为 9、15、7。
得到叶节点的最大贡献值之后,再计算非叶节点的最大贡献值。节点 20 的最大贡献值等于 20+max(15,7)=35,节点?10 的最大贡献值等于 -10+max(9,35)=25。
复杂度分析
时间复杂度:O(N),其中 N 是二叉树中的节点个数。对每个节点访问不超过 2 次。
空间复杂度:O(N),其中 N 是二叉树中的节点个数。空间复杂度主要取决于递归调用层数,最大层数等于二叉树的高度,最坏情况下,二叉树的高度等于二叉树中的节点个数。
代码:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
int res=Integer.MIN_VALUE;//不能定义为静态,负责会保存上一次计算结果
public int maxPathSum(TreeNode root) {
getPath(root);
return res;
}
public int getPath(TreeNode node){
if(node==null){
return 0;
}
//递归遍历左节点,大于0返回
int left=Math.max(getPath(node.left),0);
//递归遍历有节点,大于0返回
int right=Math.max(getPath(node.right),0);
//更新路径
int path=left+node.val+right;
if(res<path){
res=path;
}
//返回当前节点最大路径
return node.val+Math.max(left,right);
}
}3、300.最长上升子序列
题目(中等):给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列?是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18] 输出:4 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
输入:nums = [0,1,0,3,2,3] 输出:4
示例 3:
输入:nums = [7,7,7,7,7,7,7] 输出:1
求解:
本题与53.最大子序组和的思想类似,将问题分解为求以各数组元素结尾的最大子序和。具体如下:
状态定义:dp[i] 的值代表 nums 以 nums[i] 结尾的最长子序列长度。
转移方程: 设 j∈[0,i),考虑每轮计算新 dp[i] 时,遍历 [0,i)列表区间,做以下判断:
1、当 nums[i] > nums[j] 时: nums[i] 可以接在nums[j] 之后(此题要求严格递增),此情况下最长上升子序列长度为 dp[j] + 1 ;
2、当 nums[i]<=nums[j] 时: nums[i] 无法接在nums[j] 之后,此情况上升子序列不成立,跳过。
上述所有 1. 情况 下计算出的 dp[j]+1 的最大值,为直到 i 的最长上升子序列长度(即 dp[i] )。实现方式为遍历 j 时,每轮执行 dp[i] = max(dp[i], dp[j] + 1)。
转移方程: dp[i] = max(dp[i], dp[j] + 1)? ?for? j? in? [0, i)。
初始状态:dp[i] 所有元素置 1,含义是每个元素都至少可以单独成为子序列,此时长度都为 1。
返回值:返回 dp 列表最大值,即可得到全局最长上升子序列长度。
?
复杂度分析:
时间复杂度 O(N^2)?: 遍历计算 dp列表需 O(N),计算每个dp[i] 需 O(N)。
空间复杂度 O(N) : dp列表占用线性大小额外空间。
代码:
class Solution {
public int lengthOfLIS(int[] nums) {
int len=nums.length;
if(len==0) return 0;
//以nums[i]结尾的最长递增子序列长度
int[] dp=new int[len];
//数组填充1
Arrays.fill(dp,1);
int res=0;
for(int i=1;i<len;i++){
//保证递增,遍历 i 前数组元素
for(int j=0;j<i;j++){
//找到小于自身数组元素nums[j],更新dp[i]
if(nums[i]>nums[j]){
//比较当前递增序列和经过nums[j]的递增序列长度
//若新序列更长则进行更新
dp[i]=Math.max(dp[i],dp[j]+1);
}
}
//记录最长递增子序列长度
res=Math.max(res,dp[i]);
}
return res;
}
}总结
利用动态规划解决相关最优化问题,其核心也是难点就是状态转移方程(描述子问题之间的联系)的建立,要在成分理解题意的基础上,将复杂问题分解成相互联系的子问题,找到子问题之间的联系并由此建立状态转移方程,最后根据条件确定初始值。
参考《力扣 动态规划》
https://leetcode.cn/tag/dynamic-programming/problemset/