1.问题导引：

作者在进行《算法》学习的时候，遇到了这样一个算法题，题目内容如下：

迷宫问题：

假设有一个迷宫，里面有障碍物，迷宫用二维矩阵表示，标记为0的地方表示可以通过，标记为1的地方表示障碍物，不能通过。现在给一个迷宫出口，让你判断是否可以从入口进来之后，走出迷宫，每次可以向任意方向走。

题目要求：

请使用广度优先搜索（BFS）与回溯法解决，其他不做要求。

2.问题分析：

这里题目要求使用广度优先搜索（BFS）与回溯法解决。我们可以回顾广度优先搜索与回溯法的概念与思想。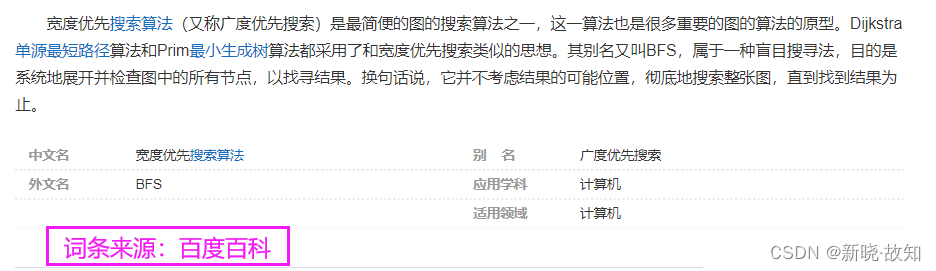

?

?

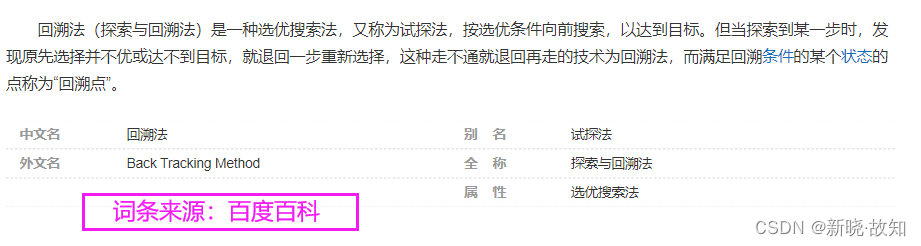
这里直接对问题进行分析解决：

举例：

?

假设这是一个4*4的迷宫，入口在(0,0)的位置，出口在(3,3)的位置，这里采用队列实现，存储迷宫中的位置，广度优先搜索属于一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。所以每一个点在走的过程中需要标记是否已经走过了。?每一步搜索过程中会进行判断，进行上、下、左、右四个方向的搜索。重复这个过程，直到走到出口为止。

代码解析这个过程，最关键的步骤用当前位置带出新的位置，新的位置可以存放在一个容器（vector）或者队列（queue）中。位置需要用坐标表示，这里封装出一个node。

??

说明：

迷宫问题其实有很多值得探讨的方向。如果有兴趣的读者，可以探讨使用BFS与回溯法求解迷宫最短路径问题，例如：输出满足要求的路径坐标以及最短路径坐标等。

作者之前学习探讨了“使用深度优先搜索（DFS）与回溯法求解迷宫问题及最短路径问题”，有兴趣的读者可以探讨交流。

<使用DFS与回溯法求解迷宫问题>文章链接：

＜迷宫问题及最短路径问题（使用DFS与回溯法求解）＞

这里由于是针对算法刷题，作者没有对探讨使用BFS与回溯法求解迷宫最短路径问题进行详细的探讨。

3.问题实现：

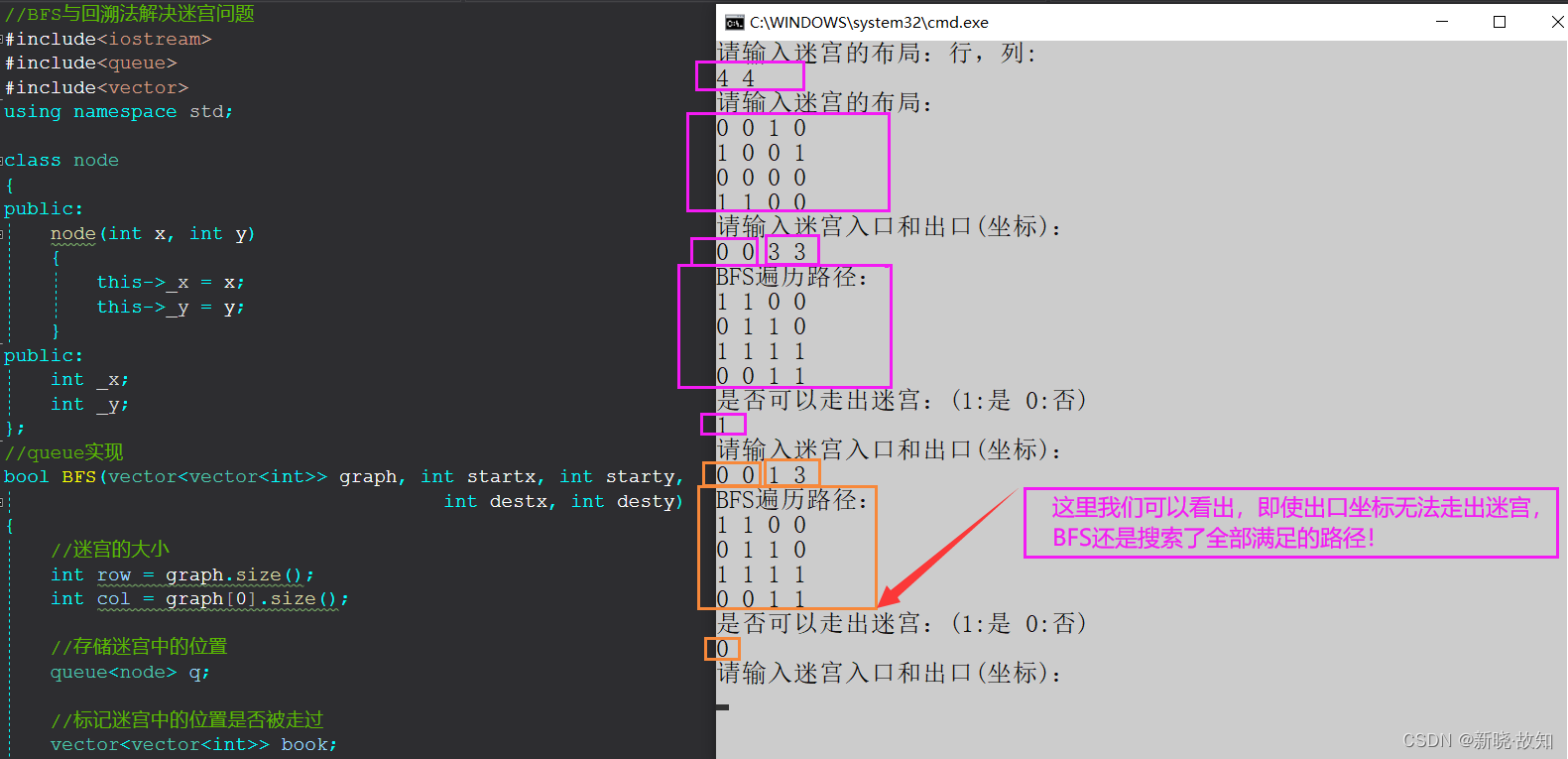
?测试用例演示：

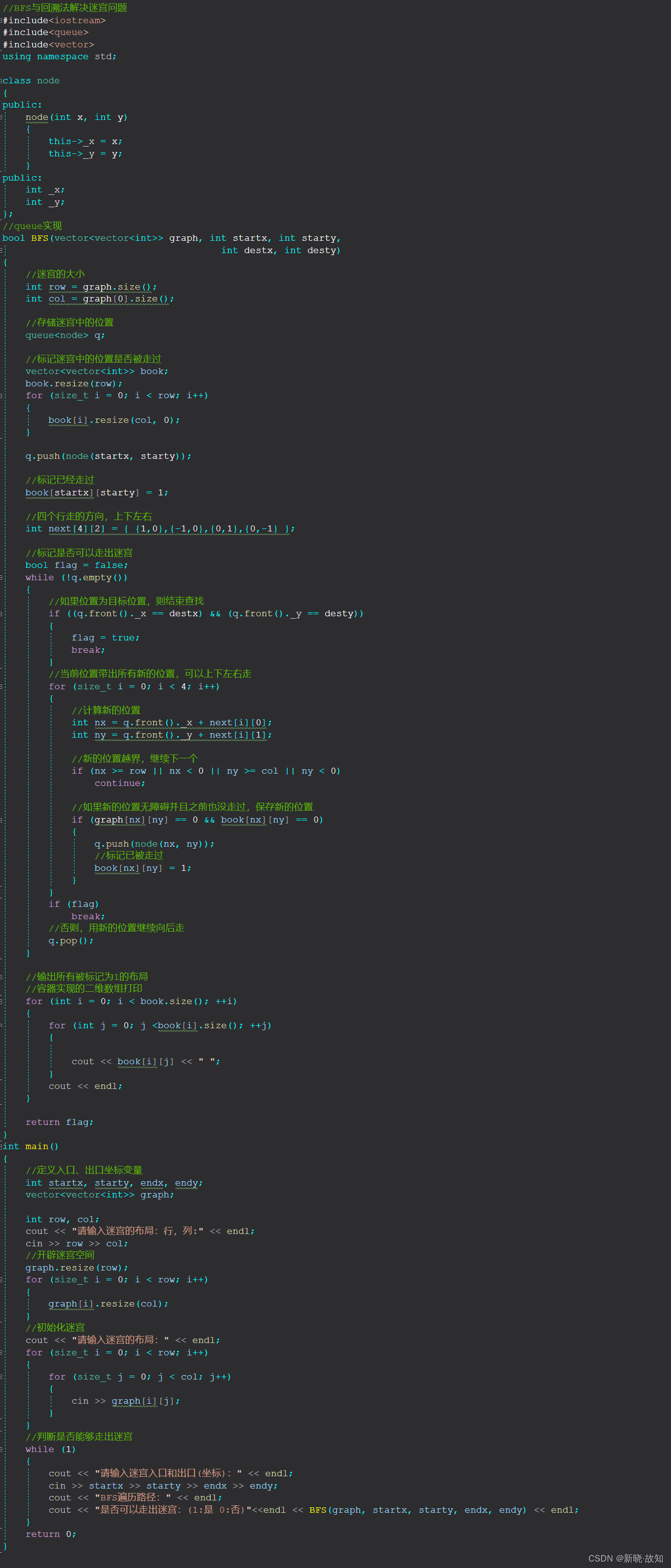
完整代码：

//BFS与回溯法解决迷宫问题
#include<iostream>
#include<queue>
#include<vector>
using namespace std;

class node
{
public:
	node(int x, int y)
	{
		this->_x = x;
		this->_y = y;
	}
public:
	int _x;
	int _y;
};
//queue实现
bool BFS(vector<vector<int>> graph, int startx, int starty, 
	                                  int destx, int desty)
{
	//迷宫的大小
	int row = graph.size();
	int col = graph[0].size();

	//存储迷宫中的位置
	queue<node> q;
	
	//标记迷宫中的位置是否被走过
	vector<vector<int>> book;
	book.resize(row);
	for (size_t i = 0; i < row; i++)
	{
		book[i].resize(col, 0);
	}
	
	q.push(node(startx, starty));

	//标记已经走过
	book[startx][starty] = 1;

	//四个行走的方向，上下左右
	int next[4][2] = { {1,0},{-1,0},{0,1},{0,-1} };

	//标记是否可以走出迷宫
	bool flag = false;
	while (!q.empty())
	{
		//如果位置为目标位置，则结束查找
		if ((q.front()._x == destx) && (q.front()._y == desty))
		{
			flag = true;
			break;
		}
		//当前位置带出所有新的位置，可以上下左右走
		for (size_t i = 0; i < 4; i++)
		{
			//计算新的位置
			int nx = q.front()._x + next[i][0];
			int ny = q.front()._y + next[i][1];

			//新的位置越界，继续下一个
			if (nx >= row || nx < 0 || ny >= col || ny < 0)
				continue;

			//如果新的位置无障碍并且之前也没走过，保存新的位置
			if (graph[nx][ny] == 0 && book[nx][ny] == 0)
			{
				q.push(node(nx, ny));
				//标记已被走过
				book[nx][ny] = 1;
			}
		}
		if (flag)
			break;
		//否则，用新的位置继续向后走
		q.pop();
	}
	
	//输出所有被标记为1的布局
	//容器实现的二维数组打印
	for (int i = 0; i < book.size(); ++i)
	{
		for (int j = 0; j <book[i].size(); ++j)
		{
			
			cout << book[i][j] << " ";
		}
		cout << endl;
	}

	return flag;
}
int main()
{
	//定义入口、出口坐标变量
	int startx, starty, endx, endy;         
	vector<vector<int>> graph;

	int row, col;
	cout << "请输入迷宫的布局：行，列:" << endl;
	cin >> row >> col;
	//开辟迷宫空间
	graph.resize(row);
	for (size_t i = 0; i < row; i++)
	{
		graph[i].resize(col);
	}
	//初始化迷宫
	cout << "请输入迷宫的布局：" << endl;
	for (size_t i = 0; i < row; i++)
	{
		for (size_t j = 0; j < col; j++)
		{
			cin >> graph[i][j];
		}
	}
	//判断是否能够走出迷宫
	while (1)
	{
		cout << "请输入迷宫入口和出口(坐标)：" << endl;
		cin >> startx >> starty >> endx >> endy;
		cout << "BFS遍历路径：" << endl;
		cout << "是否可以走出迷宫：(1:是 0:否)"<<endl << BFS(graph, startx, starty, endx, endy) << endl;
	}
	return 0;
}