[数据结构与算法] 力扣刷题day14|104二叉树的最大深度、559N叉树的最大深度、111二叉树的最小深度、222完全二叉树的节点个数

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 力扣刷题day14|104二叉树的最大深度、559N叉树的最大深度、111二叉树的最小深度、222完全二叉树的节点个数 -> 正文阅读

[数据结构与算法]力扣刷题day14|104二叉树的最大深度、559N叉树的最大深度、111二叉树的最小深度、222完全二叉树的节点个数

文章目录

104. 二叉树的最大深度

力扣题目链接

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

返回它的最大深度 3 。

层序遍历思路

就是层序遍历

public int maxDepth(TreeNode root) {
    Deque<TreeNode> que = new ArrayDeque<>();

    if (root != null) {
        que.offer(root);
    }
    int size; // 记录每层大小
    int depth = 0; // 记录深度
    while (!que.isEmpty()) {
        size = que.size();
        depth++;
        while (size-- > 0) {
            TreeNode node = que.poll();
            // 每出队一个节点，就要让他的左右子树入队
            if (node.left != null) {
                que.offer(node.left);
            }
            if (node.right != null) {
                que.offer(node.right);
            }

        }
    }

    return depth;
}

递归思路

首先要搞清楚什么是深度，什么是高度

二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数后者节点数（取决于高度从0开始还是从1开始）

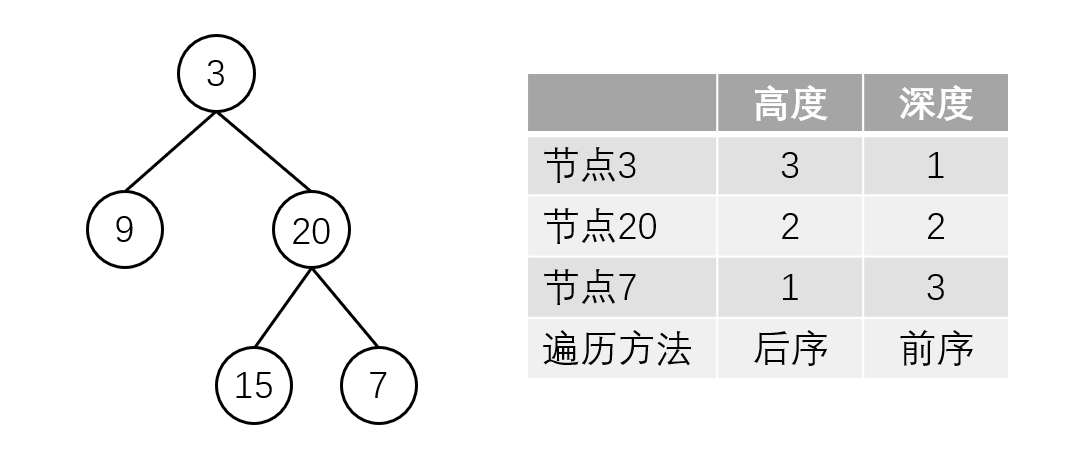
而根节点的高度就是二叉树的最大深度，所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。

难点

为什么要用后序

因为最后要用的是根节点的高度来表示最大深度，求高度就要从下往上求，而后序遍历中，最后处理的是中，可以把叶子节点的信息返回给父节点，父节点知道了孩子节点的高度再+1
递归三要素

确定递归函数的参数和返回值：参数就是传入树的根节点，返回就返回这棵树的深度，所以返回值为int类型。

public int maxDepth1(TreeNode root)

确定终止条件：最后遍历到叶子节点的左右节点会是null，如果为空节点的话，就返回0，表示高度为0。

if (node == NULL) return 0;

确定单层递归的逻辑：先求它的左子树的深度，再求的右子树的深度，最后取左右深度最大的数值再+1 （加1是因为算上当前中间节点）就是目前节点为根节点的树的深度。

// 后序遍历：左右中
int leftDepth = maxDepth1(root.left); // 左
int rightDepth = maxDepth1(root.right); // 右
return Math.max(leftDepth, rightDepth) + 1; // 中

完整代码：

// 递归-----------------------------------------------------------
public int maxDepth1(TreeNode root) {
    if (root == null) {
        return 0;
    }
    // 后序遍历：左右中
    int leftDepth = maxDepth1(root.left); // 左
    int rightDepth = maxDepth1(root.right); // 右
    return Math.max(leftDepth, rightDepth) + 1; // 中

}
// 递归-----------------------------------------------------------

559. N 叉树的最大深度

给定一个 N 叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔（请参见示例）。

示例1：

输入：root = [1,null,3,2,4,null,5,6]
输出：3

示例2：

输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：5

思路

和二叉树求最大深度一样用后序

// 递归-----------------------------------------------------------
public int maxDepth(Node root) {
    if (root == null) {
        return 0;
    }

    int depth = 0;

    for (Node child : root.children) {
        int childDepth = maxDepth(child);
        depth = Math.max(depth, childDepth);
    }
    return depth + 1;
}
// 递归-----------------------------------------------------------

111. 二叉树的最小深度

力扣题目链接

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

**说明：**叶子节点是指没有子节点的节点。

层序遍历思路

层序遍历，只有当左右孩子都为空的时候，才说明遍历的最低点了。如果其中一个孩子为空则不是最低点

如果当前节点的左右孩子都为空，直接返回最小深度

if (node.left == null && node.right == null){
    return depth;
}

完整代码

public int minDepth(TreeNode root) {
    Deque<TreeNode> que = new ArrayDeque<>();

    if (root != null) {
        que.offer(root);
    }
    int size; // 记录每层大小
    int depth = 0; // 记录深度
    while (!que.isEmpty()) {
        size = que.size();
        depth++;
        while (size-- > 0) {
            TreeNode node = que.poll();
            
            // 如果当前节点的左右孩子都为空，直接返回最小深度
            if (node.left == null && node.right == null){
                return depth;
            }
            // 每出队一个节点，就要让他的左右子树入队
            if (node.left != null) {
                que.offer(node.left);
            }
            if (node.right != null) {
                que.offer(node.right);
            }

        }
    }

    return depth;
}

递归思路

最小深度是从根节点到最近叶子节点的最短路径上的节点数量，根节点的最小高度就是要求的最小深度

递归三要素：

确定递归函数的参数和返回值：参数为要传入的二叉树根节点，返回的是int类型的深度。

public int minDepth(TreeNode root)

确定终止条件：终止条件也是遇到空节点返回0，表示当前节点的高度为0。

if (root == null) {
    return 0;
}

确定单层递归的逻辑

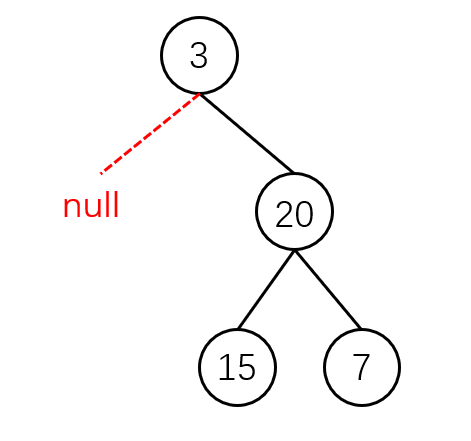
如图所示的情况并不能说最小深度为1.null并不能算作叶子节点，只有当左右孩子都为空的时候，才说明遍历的最低点了

如果左子树为空，右子树不为空，说明最小深度是 1 + 右子树的深度。

如果右子树为空，左子树不为空，最小深度是 1 + 左子树的深度。

最后如果左右子树都不为空，返回左右子树深度最小值 + 1 。

int leftDepth = minDepth(root.left);
int rightDepth = minDepth(root.right);
if (root.left == null) {
    return rightDepth + 1;
}
if (root.right == null) {
    return leftDepth + 1;
}
// 左右结点都不为null
return Math.min(leftDepth, rightDepth) + 1;

完整代码：

// 递归-----------------------------------------------------------
public int minDepth1(TreeNode root) {
    if (root == null) {
        return 0;
    }
    int leftDepth = minDepth1(root.left);
    int rightDepth = minDepth1(root.right);
    if (root.left == null) {
        return rightDepth + 1;
    }
    if (root.right == null) {
        return leftDepth + 1;
    }
    // 左右结点都不为null
    return Math.min(leftDepth, rightDepth) + 1;
}
// 递归-----------------------------------------------------------

222. 完全二叉树的节点个数

力扣题目链接

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例1：

输入：root = [1,2,3,4,5,6]
输出：6

示例2：

输入：root = []
输出：0

示例3：

输入：root = [1]
输出：1

普通二叉树递归思路

求普通二叉树的节点个数

public int countNodes1(TreeNode root) {
    if (root == null) {
        return 0;
    }
    int leftNum = countNodes1(root.left);
    int rightNum = countNodes1(root.right);
    return leftNum + rightNum + 1;
}

满二叉树递归思路

这道题可以利用完全二叉树的性质来做，在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1) 个节点。

难点

完全二叉树只有两种情况：

就是满二叉树

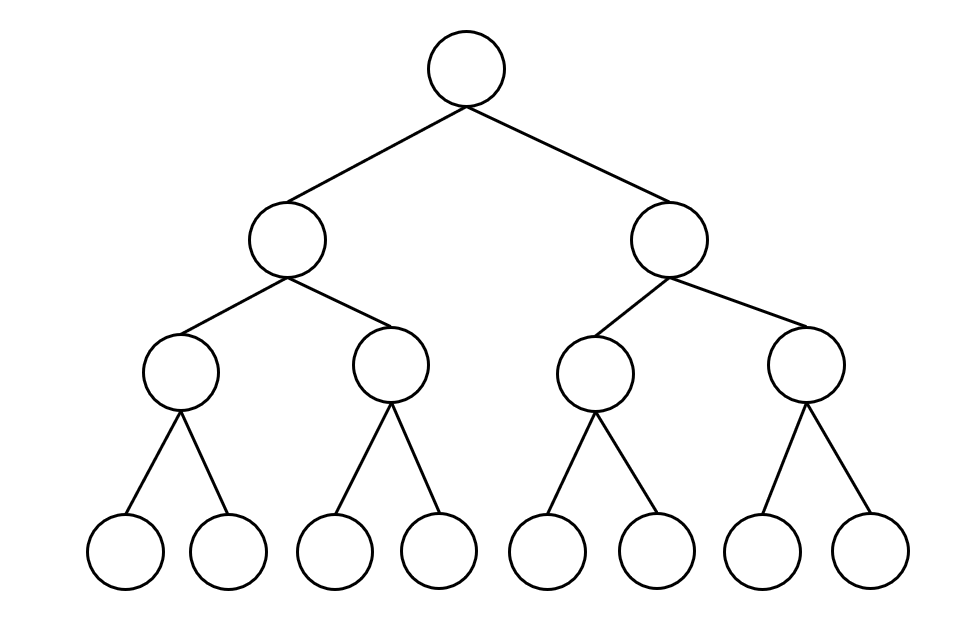
此时可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。

不是满二叉树但可以找到二叉树：分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。

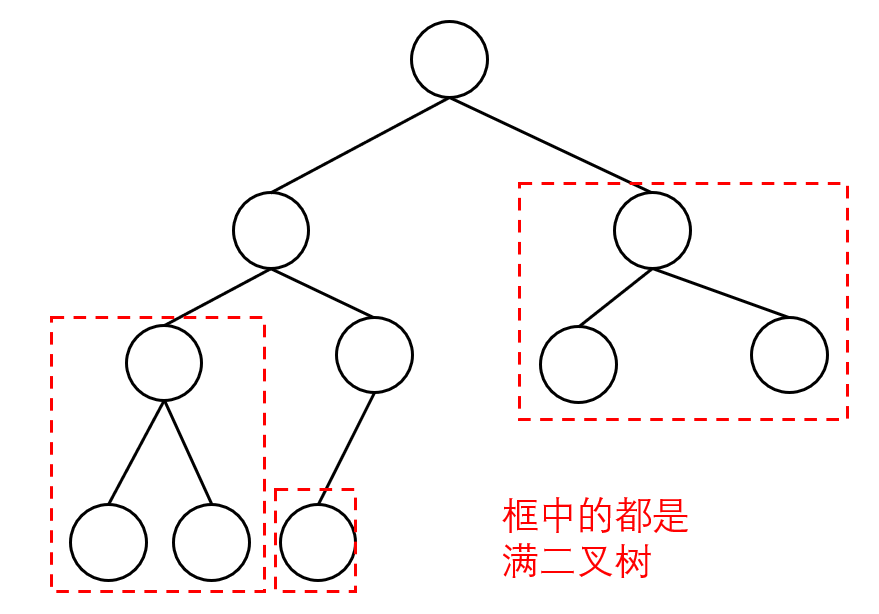
那么怎么判断一个左子树或者右子树是不是满二叉树呢？

在完全二叉树中，如果递归向左遍历的深度等于递归向右遍历的深度，那说明就是满二叉树

在完全二叉树中，如果递归向左遍历的深度不等于递归向右遍历的深度，则说明不是满二叉树

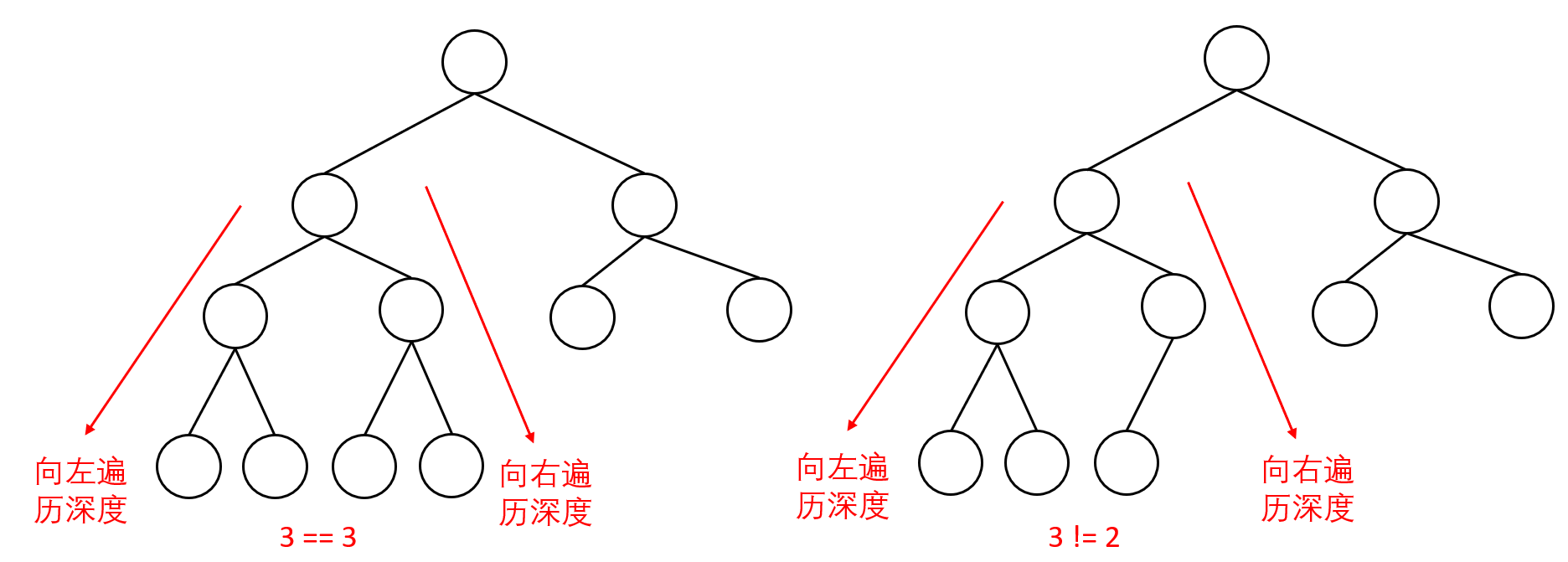
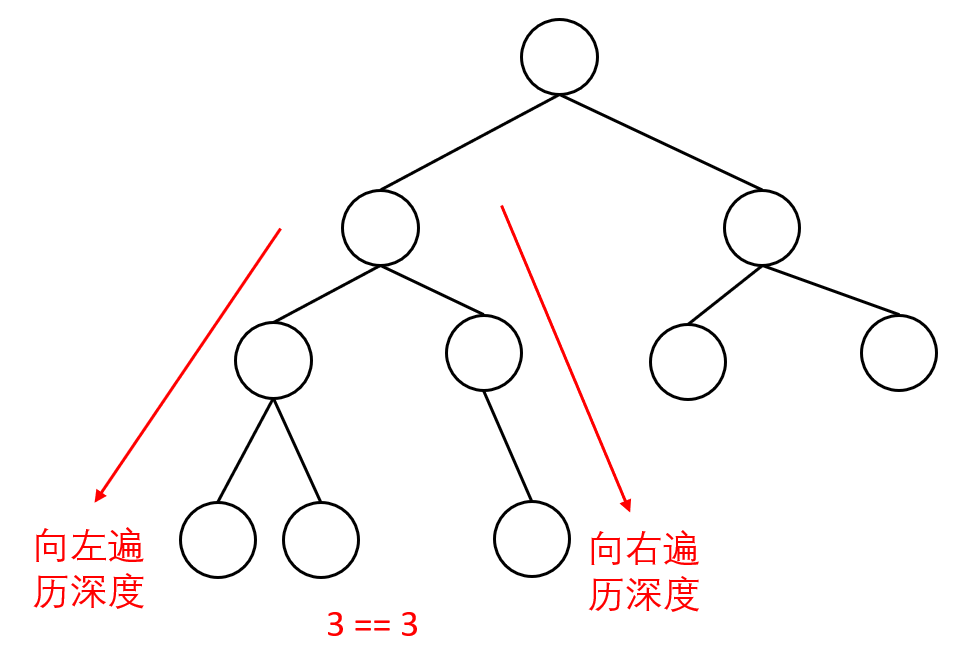
下面这种递归向左遍历的深度等于递归向右遍历的深度，但也不是满二叉树的情况不会存在。因为不是完全二叉树了。

递归三要素

确定递归函数的参数和返回值：参数就是传入树的根节点，返回就返回以该节点为根节点二叉树的节点数量，所以返回值为int类型。

public int countNodes(TreeNode root)

确定终止条件：

if (root == null) {
    return 0;
}
// 定义左右指针，计算左右侧深度
TreeNode left = root.left;
TreeNode right = root.right;
// 定义左右侧深度
int leftDepth = 0;
int rightDepth = 0;

// 求左子树深度
while (left != null) {
    left = left.left;
    leftDepth++;
}
// 求右子树深度
while (right != null) {
    right = right.left;
    rightDepth++;
}
if (leftDepth == rightDepth) {
    return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2，返回满足满二叉树的子树节点数量
}

要判断递归到的满二叉树是不是

确定单层递归的逻辑：先求它的左子树的节点数量，再求的右子树的节点数量，最后取总和再加一（加1是因为算上当前中间节点）就是目前节点为根节点的节点数量。

int leftTreeNum = countNodes(root->left);       // 左
int rightTreeNum = countNodes(root->right);     // 右
int result = leftTreeNum + rightTreeNum + 1;    // 中
return result;

完整代码：

public int countNodes(TreeNode root) {
    if (root == null) {
        return 0;
    }
    // 定义左右指针，计算左右侧深度
    TreeNode left = root.left;
    TreeNode right = root.right;
    // 定义左右侧深度
    int leftDepth = 0;
    int rightDepth = 0;

    // 求左子树深度
    while (left != null) {
        left = left.left;
        leftDepth++;
    }
    // 求右子树深度
    while (right != null) {
        right = right.right;
        rightDepth++;
    }
    if (leftDepth == rightDepth) {
        return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2，返回满足满二叉树的子树节点数量
    }

    int leftTreeNum = countNodes(root.left);       // 左
    int rightTreeNum = countNodes(root.right);     // 右
    int result = leftTreeNum + rightTreeNum + 1;    // 中
    return result;
}

迭代思路

就是层序遍历

完整代码：

public int countNodes(TreeNode root) {
    if (root == null) return 0;
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    int result = 0;
    while (!queue.isEmpty()) {
        int size = queue.size();
        while (size -- > 0) {
            TreeNode cur = queue.poll();
            result++;
            if (cur.left != null) queue.offer(cur.left);
            if (cur.right != null) queue.offer(cur.right);
        }
    }
    return result;
}