目录
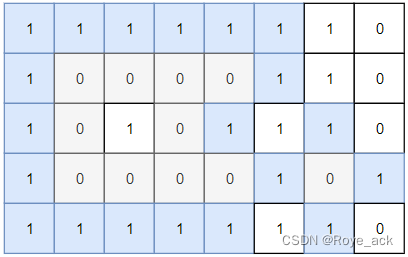
二维矩阵 grid?由 0?(土地)和 1?(水)组成。岛是由最大的4个方向连通的 0?组成的群,封闭岛是一个?完全 由1包围(左、上、右、下)的岛。
请返回 封闭岛屿 的数目。
输入:grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
输出:2
解释:
灰色区域的岛屿是封闭岛屿,因为这座岛屿完全被水域包围(即被 1 区域包围)思路:统计不连接边界的土地连通块数量
方法一:DFS?
以某个不是边界的陆地为根节点 向四周拓展(dfs)
同时把该点改为陆地 代替st数组 下次遍历就不用再次遍历这个点了
如果向四周拓展? 遇到海洋就返回true? ?如果拓展到超过边界就返回false
从该点回溯 如果四周全是海洋?则该分支满足封闭岛条件 res+1
class Solution {
public:
int n,m;
int dx[4]={1,-1,0,0},dy[4]={0,0,-1,1};
bool dfs(vector<vector<int>>&g,int x,int y)
{
if(x<0||x>m-1||y<0||y>n-1) return false; //如果遍历的这个点超出范围 说明不是封闭岛
if(g[x][y]) return true;
g[x][y]=1; //已经探索过的点标为1 防止再探索
bool f=true;
for(int i=0;i<4;i++)
{
int a=x+dx[i],b=y+dy[i];
if(!dfs(g,a,b)) f=false; //这里必须要将四个方向都跑完,不能遇到一个为false就返回
}
return f;
}
int closedIsland(vector<vector<int>>& g) {
m=g.size(),n=g[0].size();
int res=0;
for(int i=0;i<m;i++)
for(int j=0;j<n;j++)
if(g[i][j]==0)
{
if(i==0||i==m-1||j==0||j==n-1) continue; //如果该点已经是边界点了 则跳过该点
if(dfs(g,i,j)) res++; //如果该连通块满足封闭岛条件 res++
}
return res;
}
};方法二:BFS
- BFS是用队列来实现的,我们先将当前陆地的位置加入到队列中,然后取出当前位置,并将它标记为1,表示它已经遍历过了。
- 最后将它四个方向也为陆地的位置加入到队列中,一直循环,直到队列为空。
- 在循环的过程中我们需要判断是否走出了边界,如果走出了边界就说明该位置所在的岛屿不是封闭岛屿。
typedef pair<int,int> PII;
class Solution {
public:
int n,m;
int dx[4]={1,-1,0,0},dy[4]={0,0,-1,1};
bool bfs(vector<vector<int>>&g,int x,int y)
{
queue<PII>q;
q.push({x,y});
if(x<0||x>m-1||y<0||y>n-1) return false; //如果遍历的这个点超出范围 说明不是封闭岛
bool f=true;
while(!q.empty())
{
auto t=q.front();
q.pop();
g[t.first][t.second]=1;
for(int i=0;i<4;i++)
{
int a=t.first+dx[i],b=t.second+dy[i];
if(g[a][b]) continue;
g[a][b]=1;
if(a<0||a>m-1||b<0||b>n-1) f=false; //这里必须要将四个方向都跑完,不能遇到一个为false就返回
q.push({a,b});
}
}
return f;
}
int closedIsland(vector<vector<int>>& g) {
m=g.size(),n=g[0].size();
int res=0;
for(int i=0;i<m;i++)
for(int j=0;j<n;j++)
if(g[i][j]==0)
{
if(i==0||i==m-1||j==0||j==n-1) continue; //如果该点已经是边界点了 则跳过该点
if(bfs(g,i,j)) res++; //如果该连通块满足封闭岛条件 res++
}
return res;
}
};?