[数据结构与算法]力扣 每日一题 927. 三等分【难度：困难】

题目链接

https://leetcode.cn/problems/three-equal-parts/

思路

为了方便表述，本文将数组或子数组称之为“字符串”或“子串”。

本题的关键在于发现：

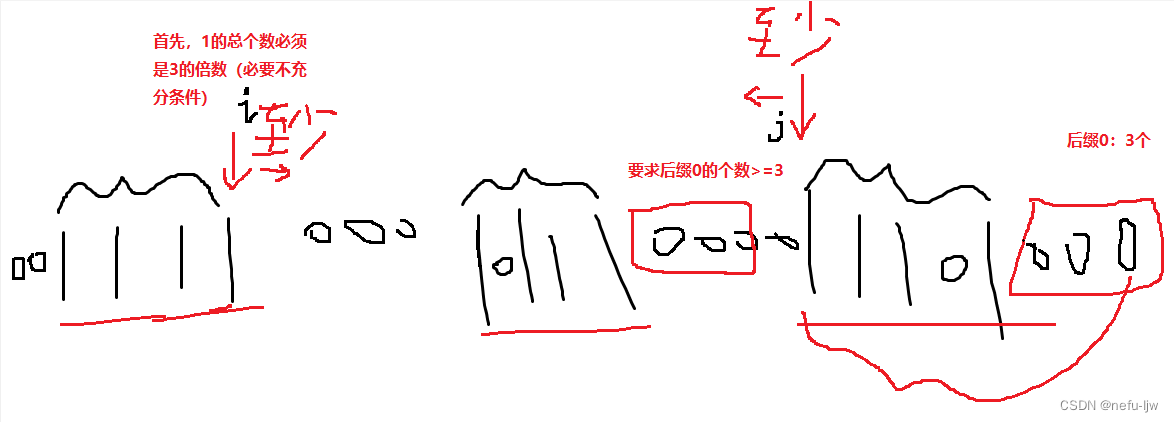
1. 字符串能被三等分 => 1的总个数必须是3的倍数。必须满足这个必要条件。
2. 第3个子串的结束位置被固定在串的末尾，那么第3个子串的后缀0的个数suffix_zero_count，能用于限制前面第1、2个子串的后缀0个数。因为第3个子串的后缀0是固定的，而前面的两个子串的后缀0是可以往后调整的，只要它们的后缀0个数>=suffix_zero_count，多余的后缀0就可以划分给下一个子串作为前导0。通过这种调整，确定了第1、2个子串的结束位置，同时也确定了第2、3个子串的开始位置（第1个子串的开始位置被固定在串的开头）。
3. 最后直接得到三个子串的起始和终点位置，依次比对是否相等即可。

放一个图便于理解：

代码

先切分得到string，再用其初始化bitset，bitset能直接判断是否相等（包括前导0也没有问题）。

class Solution {
public:
    vector<int> threeEqualParts(vector<int>& arr) {
        int sz=arr.size();
        vector<int> ans;
        string str;
        int count=0; // 1的总个数
        for(auto &x:arr){
            if(x==1){
                count++;
            }
            str+=(x+'0'); // arr to string
        }
        // 全是0，没有1，可以任意划分，只要不超过边界即可
        if(count==0){
            return {0,sz-1};
        }
        // 1的个数不是3的倍数，划分失败
        if(count%3!=0){
            return {-1,-1};
        }
        int ave_count=count/3; // 每个子串含有的1的个数
        int end_pos1=-1,start_pos2=-1,end_pos2=-1,start_pos3=-1,end_pos3=-1;
        int now_count=0;
        for(int i=0;i<sz;i++){
            if(arr[i]==1){
                now_count++;
                if(now_count==ave_count){
                    end_pos1=i; // 第1个子串中最后一个1的位置
                }
                if(now_count==ave_count+1){
                    start_pos2=i; // 第2个子串中第一个1的位置
                }
                if(now_count==ave_count*2){
                    end_pos2=i; // 第2个子串中最后一个1的位置
                }
                if(now_count==ave_count*2+1){
                    start_pos3=i; // 第3个子串中第一个1的位置
                }
                if(now_count==(ave_count*3)){
                    end_pos3=i; // 第3个子串中最后一个1的位置
                }
            }
        }

        // 第3个子串后缀0的区间[end_pos3+1, sz)
        int suffix_zero_count=sz-end_pos3-1; // 第3个子串的后缀0个数
        if(start_pos3-end_pos2-1<suffix_zero_count || start_pos2-end_pos1-1<suffix_zero_count){
            // 第2个子串后缀0的区间[end_pos2+1,start_pos3)
            // 第1个子串后缀0的区间[end_pos1+1,start_pos2)
            // 若第1个子串或第2个子串的后缀0个数不够第3个子串的后缀0个数，则划分失败
            return {-1,-1};
        }
        
        // 切分得到s1
        int suffix_end_pos1=end_pos1+suffix_zero_count; // s1加上后缀0，调整s1的结束位置
        assert(suffix_end_pos1<start_pos2);
        string s1=str.substr(0,suffix_end_pos1+1); // [0,suffix_end_pos1]
		
        // 切分得到s2
        int suffix_end_pos2=end_pos2+suffix_zero_count; // s2加上后缀0，调整s2的结束位置
        assert(suffix_end_pos2<start_pos3);
        string s2=str.substr(start_pos2,suffix_end_pos2-start_pos2+1); // [start_pos2,suffix_end_pos2]
		
        // 切分得到s3
        string s3=str.substr(start_pos3); // [start_pos3,sz)

        bitset<30000> t1(s1);
        bitset<30000> t2(s2);
        bitset<30000> t3(s3);
        if(t1==t2&&t2==t3){ // bitset直接判断是否相等
            return {suffix_end_pos1,suffix_end_pos2+1};
        }else{
            return {-1,-1};
        }
    }
};

/*
[1,0,1,0,1]
ans: [0,3]

[1,1,1,0,0,1,1,0,1,0,1,1,1,1,1,1]
ans: [-1,-1]
*/