[数据结构与算法]【数据结构与算法】堆排序算法的介绍和程序实现

1. 堆排序的介绍

堆排序算法是顺序储存二叉树的实际应用，顺序储存二叉树参考地址

堆排序是一种选择排序算法，它的最坏，最好，平均时间复杂度均为$O(nlogn)$，它也是不稳定排序

当完全二叉树每个节点的值都大于或等于其左右子节点的值，称为大顶堆，升序排序时使用；当完全二叉树每个节点的值都小于或等于其左右子节点的值，称为小顶堆，降序排序时使用。如下所示就是一个大顶堆：

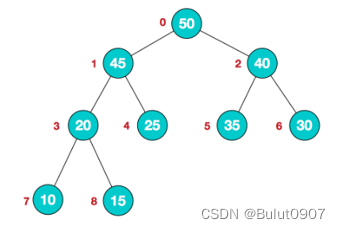
其对应的数组就是

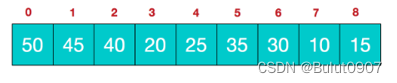
所以大顶堆对应数组的元素大小关系为：$array[n]>=array[2?n+1]$ && $array[n]>=array[2?n+2]$，n为数组的index

2. 堆排序的基本思想

1. 将待排序序列构造成一个大顶堆，此时整个序列的最大值就是堆顶的root节点
2. 将root节点对应的元素与序列末尾的元素进行交换，此时序列的末尾就是最大值
3. 然后将剩余n-1个元素重新构造成一个大顶堆，这样会得到n个元素的次小值
4. 如此反复执行，便能得到一个有序序列

使用大顶堆进行升序排序的例子：
步骤1：构建初始堆如下：

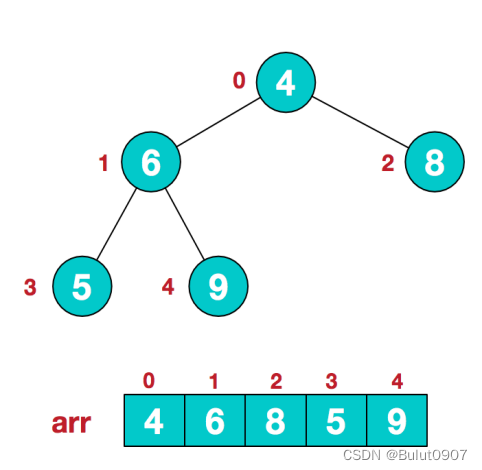
步骤二：因为叶子节点不用调整，只需调整非叶子节点，调整顺序为先右后左 + 先下后上。而第一个非叶子节点的index为$arr.length/2?1=5/2?1=1$，也就是值为6的节点，第一个非叶子节点调整后如下所示

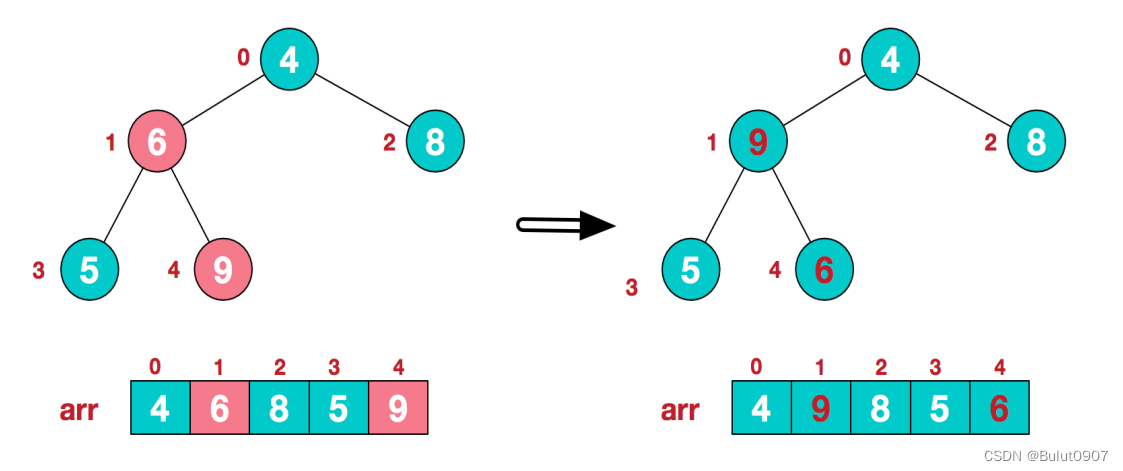
步骤三：第二个非叶子节点的值为4，调整后如下所示

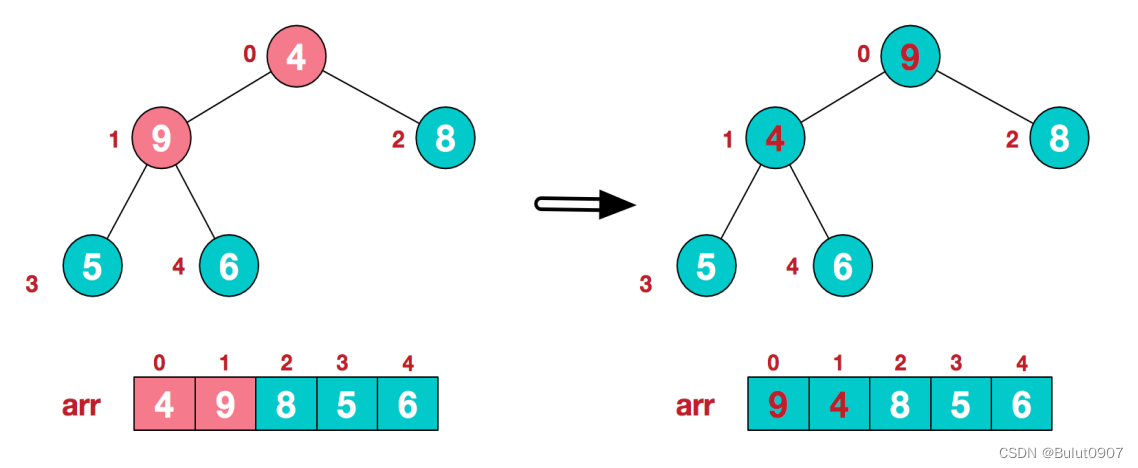步骤四：前面的步骤导致子树[4, 5, 6]的结构混乱，需重新调整，调整后如下所示：
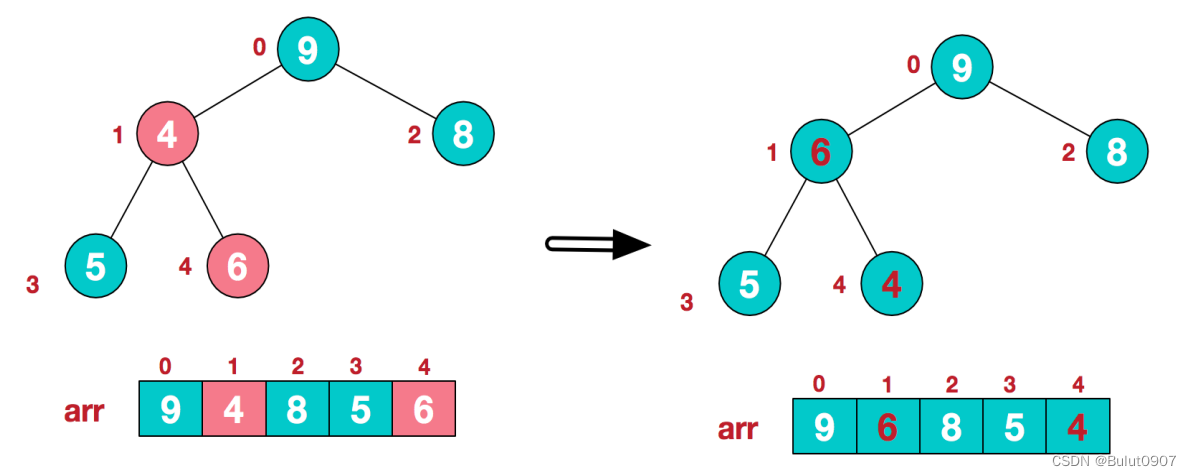步骤五：此时构造出了一个大顶堆，将堆顶对应的元素和arr末尾对应的元素进行交换，得到第一个最大值。如下所示：

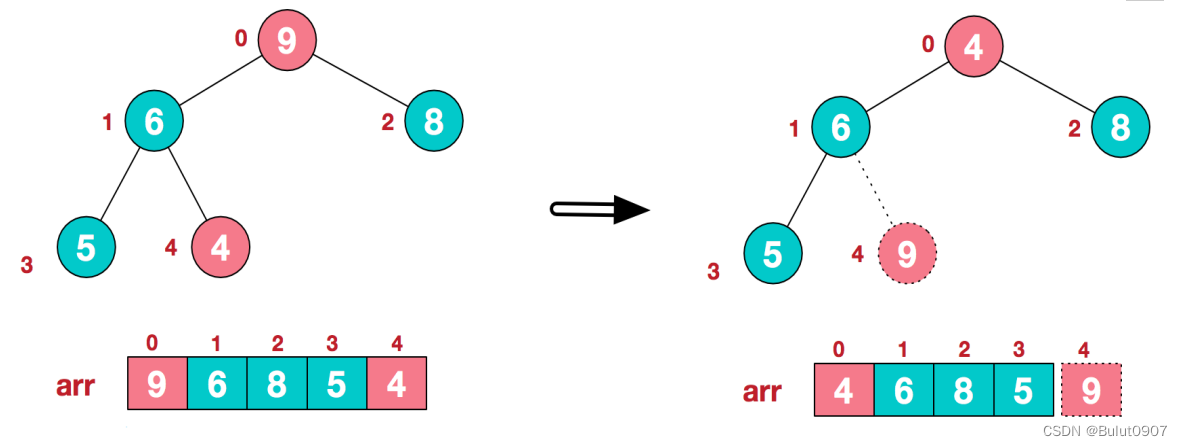
步骤六：对剩余的n-1个元素构成的堆，继续构建大顶堆，如下所示：

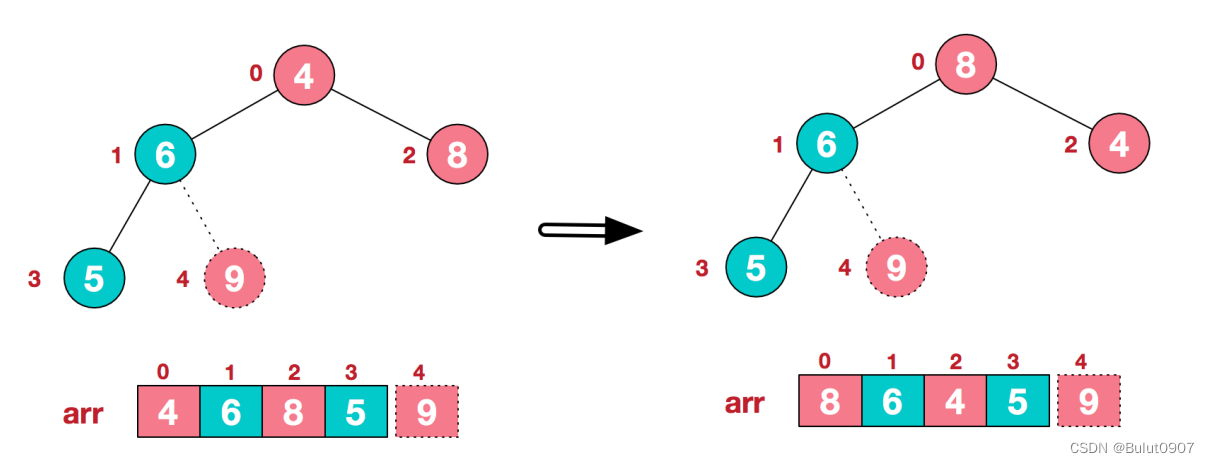步骤七：再将堆顶对应的元素和arr末尾对应的元素进行交换，得到第二大值。如下所示：

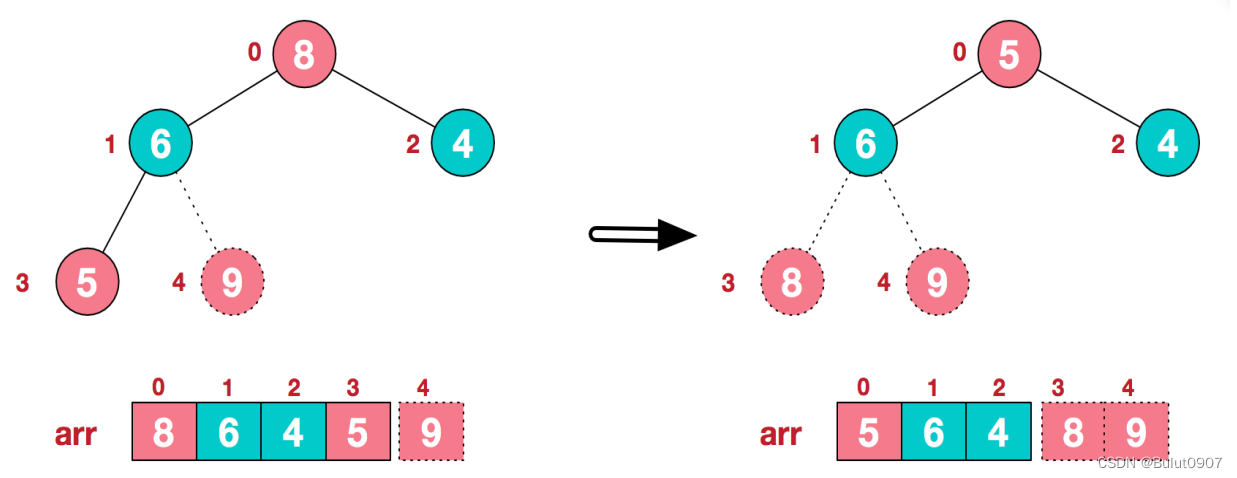
步骤八：后续继续进行调整、交换，如此反复进行，最终使得整个序列有序，如下所示：

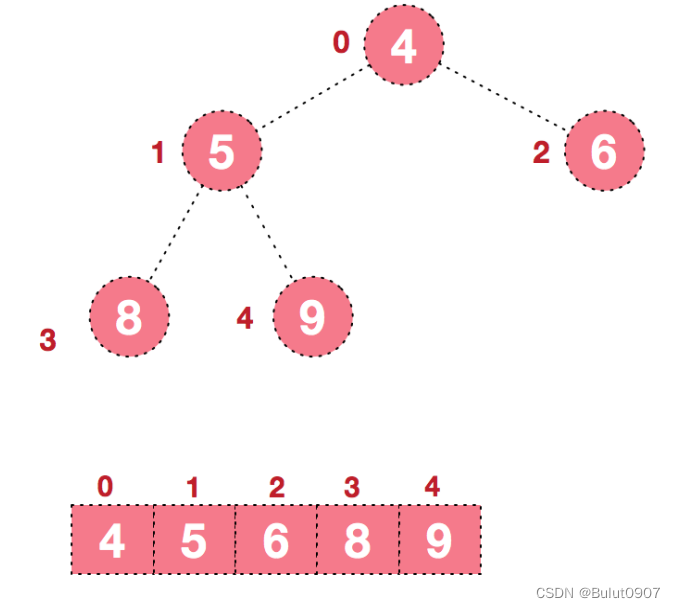
3. 堆排序的程序实现

需求：有一组无序的数据{4, 6, 8, 5, 9}，请用堆排序算法实现从小到大排列

程序如下：

import java.util.Arrays;

public class HeapSort {

    public static void main(String[] args) {
        int[] array = {4, 6, 8, 5, 9};

        // 使用堆排序算法，对数组进行升序排列
        heapSort(array);

        System.out.println("堆排序后 " + Arrays.toString(array));
    }

    // 堆排序算法，对数组进行升序排列实现
    public static void heapSort(int[] array) {

        // 第一次将整颗树构建成大顶堆，是先右后左，先下后上的顺序将各颗子树构建成(每一颗子树构建都会调用一次adjustHeap)大顶堆
        for (int index = array.length / 2 - 1; index >= 0; index--) {
            adjustHeap(array, index, array.length);
        }

        // 找出第一个最大值后，每找一个次大值时，调用一次adjustHeap
        int tmp = 0;
        for (int endIndex = array.length - 1; endIndex > 0; endIndex--) {
            // 将array[0]堆顶的最大值，和序列的最后有效元素进行交换
            tmp = array[endIndex];
            array[endIndex] = array[0];
            array[0] = tmp;

            // 交换完成后，endIndex就是序列有效元素的个数
            // 如果剩余只有一个元素，则不用进行堆调整了
            if (endIndex > 1) {
                // 此时堆顶的index就是0
                adjustHeap(array, 0, endIndex);
            }
        }

    }


    // 将顺序二叉树的一颗子树调整为大顶堆，这里有两种情况：
    // 第一种是第一次将整颗树构建成大顶堆，是先右后左，先下后上的顺序将各颗子树构建成(每一颗子树构建都会调用一次adjustHeap)大顶堆
    // 第二种是找出第一个最大值后，每找一个次大值时，调用一次adjustHeap

    // 参数array: 待调整的堆的数组
    // 参数index: 子树堆顶对应的元素在数组的index
    // 参数noAdjustNums：表示数组中剩余未调整的元素个数
    public static void adjustHeap(int[] array, int index, int noAdjustNums) {

        int tmp = array[index];

        // 此时index的左节点所在的子树中, index的左节点最大。index的右节点所在的子树，index的右节点最大
        // 第一次遍历是将index节点的值，变成其左节点和右节点的最大值，并将tmp值赋值给其左节点或右节点
        // 后面的遍历是将tmp值不断的下沉，以构建成大顶堆
        for (int nodeIndex = index * 2 + 1; nodeIndex < noAdjustNums; nodeIndex = nodeIndex * 2 + 1) {
            // 如果有右节点，且右节点大于左节点，则后面对右节点进行处理，否则对左节点进行处理。其实就是找出左右节点的最大值
            if (nodeIndex + 1 < noAdjustNums && array[nodeIndex] < array[nodeIndex + 1]) {
                nodeIndex++;
            }
            // 如果左右节点的最大值比tmp大，则将index所在的节点的值变成最大值
            // 同时将index变成之前最大值对应的index(重新变成其左子树或右子树的堆顶)
            if (array[nodeIndex] > tmp) {
                array[index] = array[nodeIndex];
                index = nodeIndex;
                // 否则，表示tmp是最大的值，表示tmp找到了合适的index进行赋值
            } else {
                break;
            }
        }
        // 遍历完成，表示tmp找到了合适的index进行赋值
        array[index] = tmp;
    }

}

运行程序，结果如下：

堆排序后 [4, 5, 6, 8, 9]