[LeetCode周赛复盘] 第 89 场双周赛20221015
一、本周周赛总结
- 没打,但是补题。
- T1暴力。
- T2幂的前缀和
- T3二分答案/dp
- T4枚举答案+子树权值和
二、 [Easy] 6208. 有效时间的数目
链接: 6208. 有效时间的数目
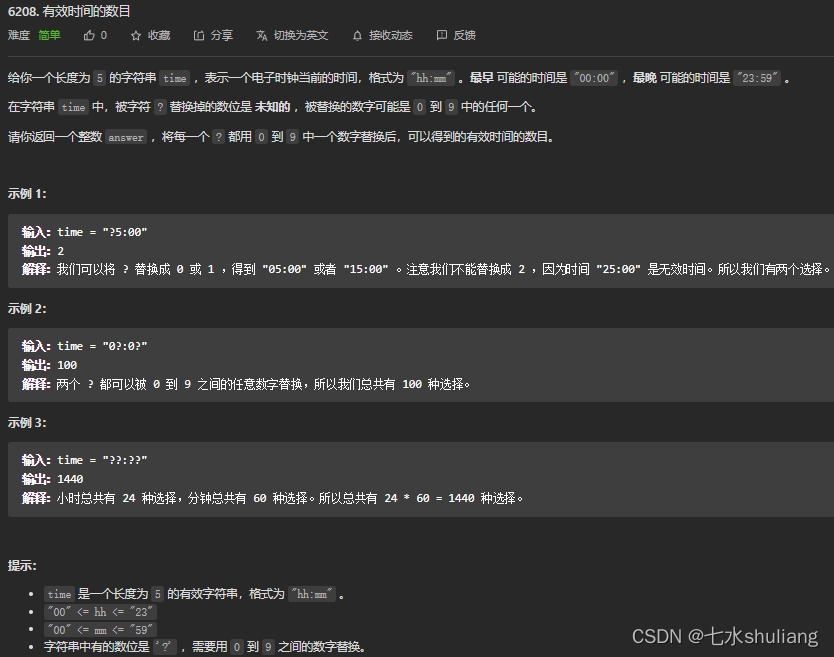
1. 题目描述
2. 思路分析
- 我写了个DFS,卡了一会,因为dfs中判断t[i]了,实际上t会被修改,因此要判断time[i]
- 还是灵神的思路写的更快,思维量小:
- 直接暴力枚举1440种情况,即枚举时分,然后判断每位是否符合即可。
3. 代码实现
class Solution:
def countTime(self, time: str) -> int:
ans = set()
t = list(time)
def ok(t):
h = int(''.join(t[:2]))
m = int(''.join(t[3:]))
return 0<=h<=23 and 0<=m<=59
def dfs(i):
if i == 5:
if ok(t):
ans.add(''.join(t))
return
if time[i] != '?':
dfs(i+1)
else:
for j in range(10):
t[i] = str(j)
dfs(i+1)
dfs(0)
return len(ans)
三、[Medium] 6209. 二的幂数组中查询范围内的乘积
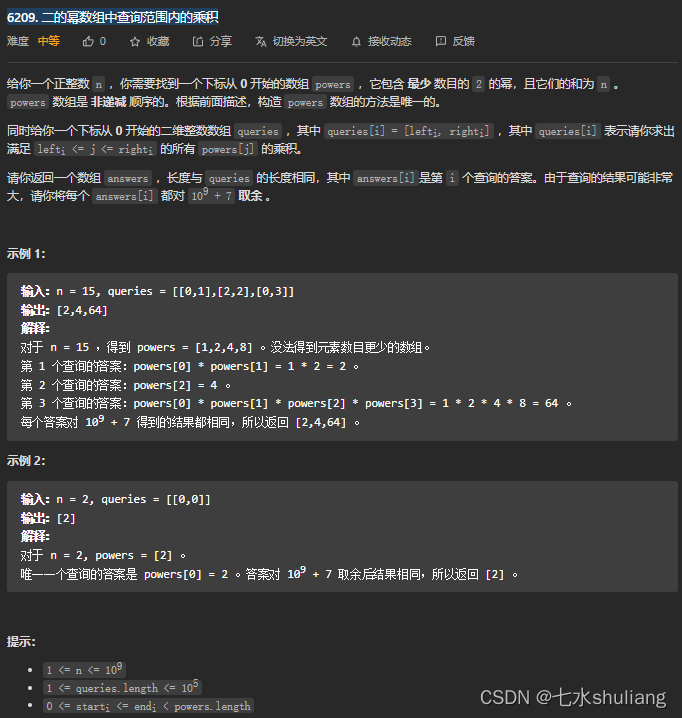
1. 题目描述
2. 思路分析
- 第一段表述有点乱,实际是把n分成x个数,每个数都是2的幂。
- 那么显然就是n的二进制上每一位1.处理出来就是power数组了。
- 我们发现power数组长度最多是30。
- 然后就可以暴力了。
- 或者前缀积。
- 这里由于是2的幂,因此可以对幂算前缀和,最后再快速幂。
- py的话直接取模即可。
- 由于q是1e5,但实际上power最多30,询问不会超过(30+1)*30//2 ,因此可以预处理一下,询问就是O1了。
- 这里我直接写了记忆化。
3. 代码实现
MOD = 10**9 + 7
class Solution:
def productQueries(self, n: int, queries: List[List[int]]) -> List[int]:
p = []
for i in range(32):
if n&(1<<i):
p.append(i)
pre = [0]+list(accumulate(p))
@cache
def calc(l,r):
return 2**(pre[r+1]-pre[l])%MOD
ans = []
for l,r in queries:
ans.append(calc(l,r))
return ans
四、[Medium] 6210. 最小化数组中的最大值
链接: 6210. 最小化数组中的最大值
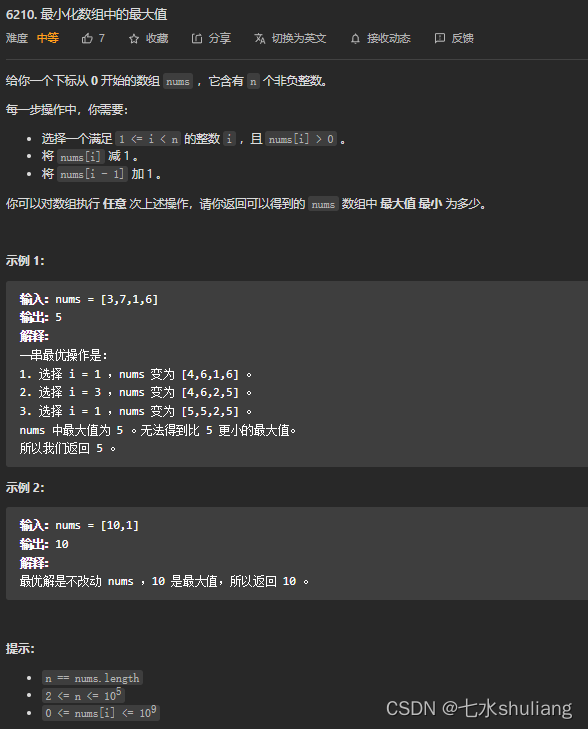
1. 题目描述
2. 思路分析
灵神说了,“最小化最大值”=二分答案
- 这里我先写了一个dp,然后再尝试灵神提示的二分。
- 定义f[i]为nums中前i个数的答案。
- 初始:显然i=0时,数组就一个数,无法操作,f[0]=a[0]。
- 转移:
- nums[i] = f[i-1] ,即对nums[i]来说,无论怎么向前匀数字,不会使前边的答案变小。
- 当nums[i]<=f[i-1],当前值小,那么不需要操作即可保持f[i-1]这个答案。
- 否则尝试向前匀,能匀成什么状态呢,显然就是平均值,那么就是前缀和除以长度向上取整。
- 二分思路。
- 我们假设答案是limit,尝试进行操作,使nums中每个数都不大于limit。看看是否能成功。
- 显然这是单调的。即:limit若可以成功,那么limit+1更可以成功;limit不能成功,limit-1更不可能。
- calc函数传入limit返回01即可。代表是否成功。
- 这里calc有两种写法,最简单的是每次copy一下原数组,然后从后向前模拟,把大于limit的部分挪给前一个数。
- 常数小一点的写法是记录每次多余的部分,最后到nums[i]判断是否还有多余的部分。
3. 代码实现
dp
class Solution:
def minimizeArrayValue(self, nums: List[int]) -> int:
n = len(nums)
pre = list(accumulate(nums))
f = [0]*n
f[0] = nums[0]
for i in range(1,n):
f[i] = f[i-1]
if nums[i]<= f[i-1]:
continue
f[i] = max(f[i], (pre[i]+i+1-1)//(i+1))
return f[-1]
二分copy写法
class Solution:
def minimizeArrayValue(self, nums: List[int]) -> int:
n = len(nums)
def calc(limit):
p = nums[:]
for i in range(n-1,0,-1):
if p[i]> limit:
p[i-1] += p[i] - limit
return int(p[0] <= limit)
return bisect_left(range(max(nums)+1),1,key= calc)
二分常数写法
class Solution:
def minimizeArrayValue(self, nums: List[int]) -> int:
n = len(nums)
def calc(limit):
p = 0
for i in range(n-1,-1,-1):
p += nums[i]
if p > limit:
p = p- limit
else:
p = 0
return int(p==0)
return bisect_left(range(max(nums)+1),1,key= calc)
五、[Hard] 6211. 创建价值相同的连通块
链接: 6211. 创建价值相同的连通块
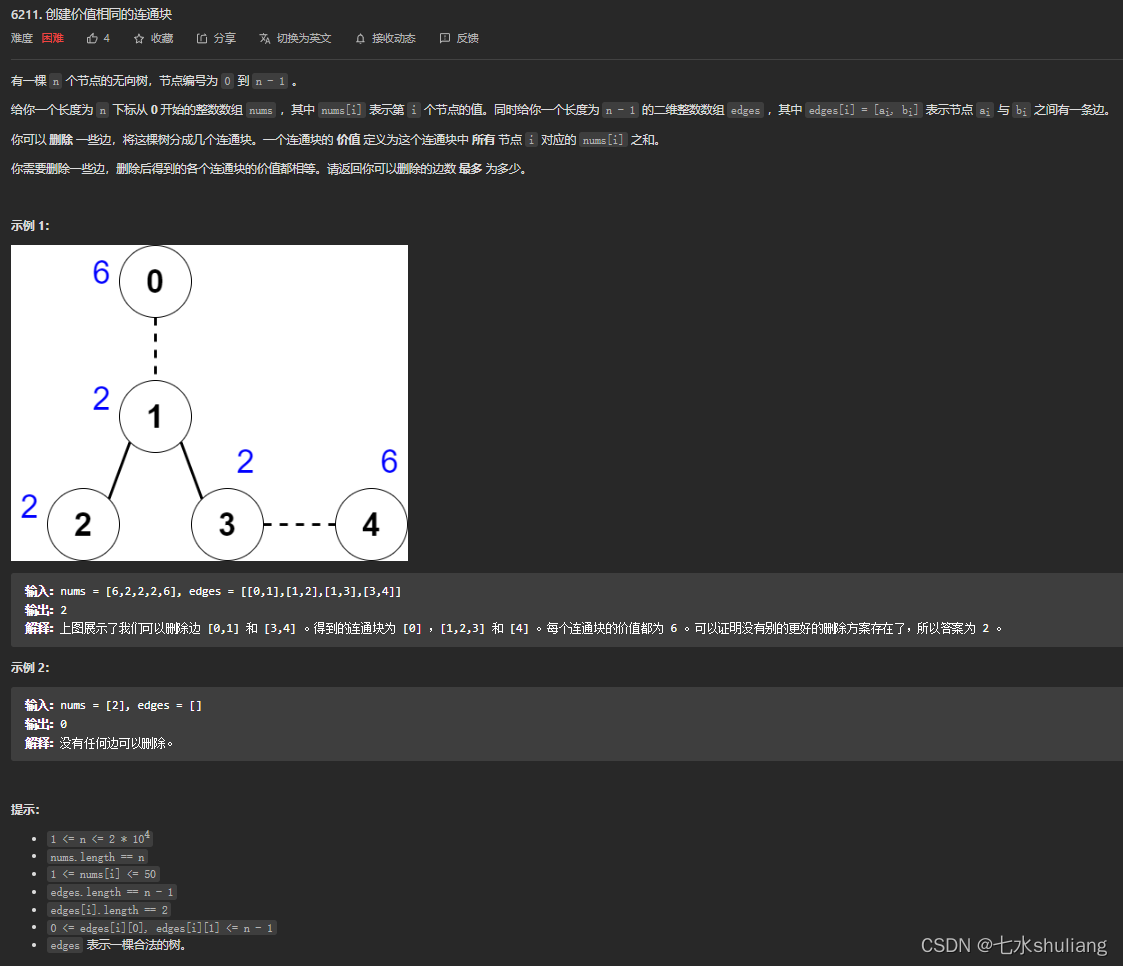
1. 题目描述
2. 思路分析
- 首先一个明显的性质,s=sum(nums),如果要把树分成权值和相同的x个连通块,那么s能整除x。
- 那么考虑枚举每个连通块的权值和i,如果能整除,那么尝试分成s//i块,删除的边数就是s//i - 1。
- 问题就剩如何尝试分成s//i块,且每块权值和是i。
- 那么按照灵神给出的计算子树权值和模板,我们试图让每个子树的价值是i。
- 显然,如果子树和超过i,不合法,可以提前返回,我们用-1标志它不合法。
- 如果子树和正好是i,那么剪掉这颗子树即可,返回0。
- 最后检查根节点所在的连通块是0即可。
def dfs(u,fa):
s = nums[u]
for v in g[u]:
if v != fa:
s += dfs(v,u)
return s
3. 代码实现
class Solution:
def componentValue(self, nums: List[int], edges: List[List[int]]) -> int:
n = len(nums)
if n == 1:
return 0
if len(set(nums)) == 1:
return n-1
g = [[] for _ in range(n)]
for u,v in edges:
g[u].append(v)
g[v].append(u)
s = sum(nums)
def dfs(u,fa):
p = nums[u]
for v in g[u]:
if v == fa:continue
z = dfs(v,u)
if z == -1:
return -1
p += z
if p>i:
return -1
return p%i
for i in range(max(nums),s//2+1): # 枚举每块连通块价值
if s % i:continue
if dfs(0,-1) == 0:
return s//i -1 # 每块连通块价值是i的话,能分s//i块
return 0