一、队列

队列是一种先入先出的数据结构

设计循环队列
class MyCircularQueue {
    
    private int[] data;
    private int head;
    private int tail;
    private int size;

    public MyCircularQueue(int k) {
        data = new int[k];
        head = -1;
        tail = -1;
        size = k;
    }
    
    public boolean enQueue(int value) {
        if (isFull() == true) {
            return false;
        }
        if (isEmpty() == true) {
            head = 0;
        }
        tail = (tail + 1) % size;
        data[tail] = value;
        return true;
    }
    
   
    public boolean deQueue() {
        if (isEmpty() == true) {
            return false;
        }
        if (head == tail) {
            head = -1;
            tail = -1;
            return true;
        }
        head = (head + 1) % size;
        return true;
    }
    
    public int Front() {
        if (isEmpty() == true) {
            return -1;
        }
        return data[head];
    }
    
    public int Rear() {
        if (isEmpty() == true) {
            return -1;
        }
        return data[tail];
    }
    
    public boolean isEmpty() {
        return head == -1;
    }
    
    public boolean isFull() {
        return ((tail + 1) % size) == head;
    }
}

二、栈

?栈是一种先入后出的数据结构

?计算逆波兰表达式

算法：遇到?数字压入数字栈中，遇到计算符号弹出两个数字，计算完压入数字栈中。

class Solution {
    public int evalRPN(String[] tokens) {
        Stack<Integer> stack=new Stack<Integer>();
        for(String s:tokens){
            if(s.equals("+")){
                int num1=stack.pop();
                int num2=stack.pop();
                stack.push(num2+num1);
            }else if(s.equals("-")){
                int num1=stack.pop();
                int num2=stack.pop();
                stack.push(num2-num1);
            }else if(s.equals("*")){
                int num1=stack.pop();
                int num2=stack.pop();
                stack.push(num2*num1);
            }else if(s.equals("/")){
                int num1=stack.pop();
                int num2=stack.pop();
                stack.push(num2/num1);
            }else{
                stack.push(Integer.parseInt(s));
            }
        }
        return stack.pop();
    }
}

三、BFS和DFS

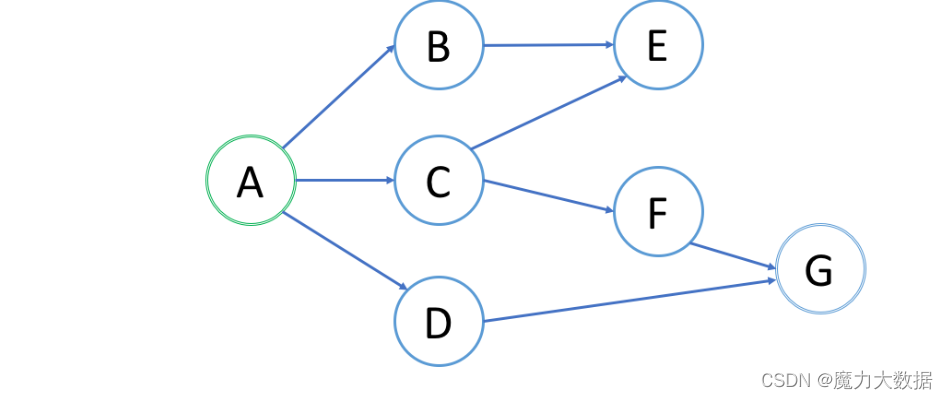
广度优先 BFS

同一层节点将在同一个循环中处理，保证每次循环结束时队列中都是同一层的元素。

即：第一次是A,第二次是BCD，第三次是EFG

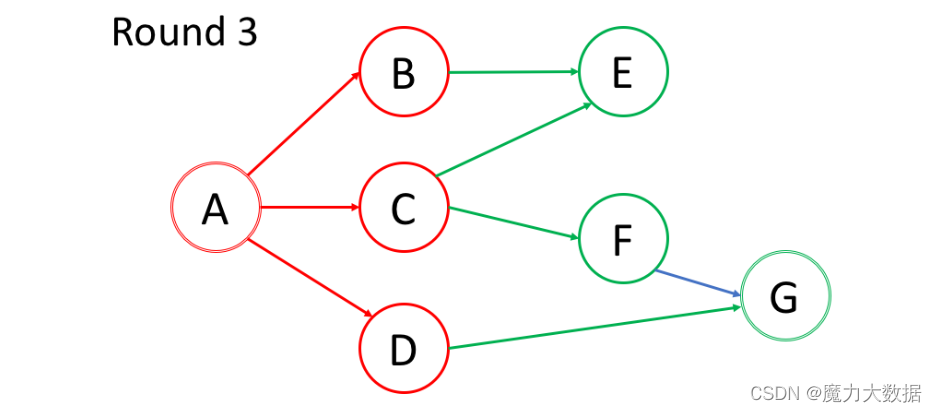
?深度优先 DFS

寻找的是路径ABECFG

BFS和DFS的运用

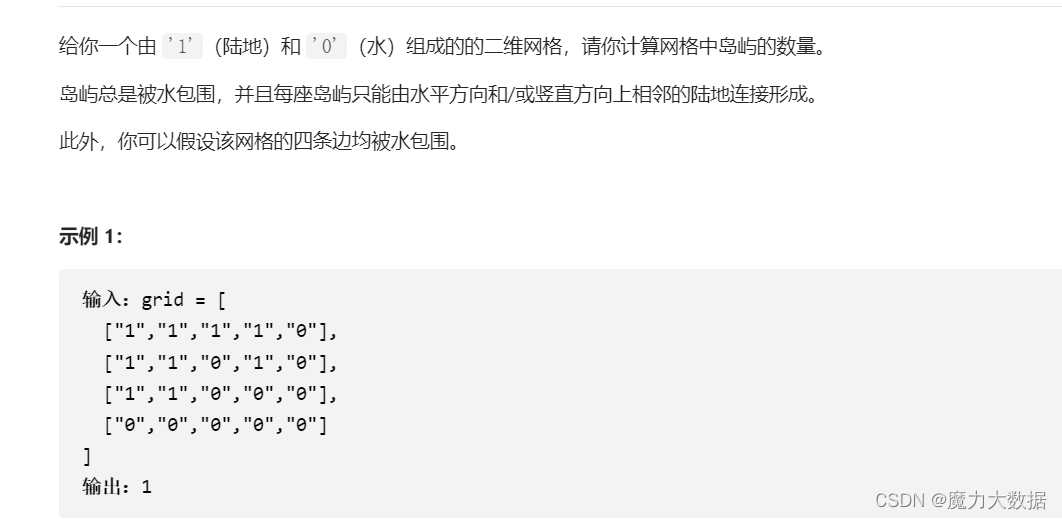
BFS：首先利用双循环遍历矩阵每个元素，若有元素为"1",则岛屿个数+1，并将该点作为参数调用BFS函数。

BFS函数：将传入的点变为''0''。建立队列，传入参数进入队列。若队列不为空，弹出队列队头元素，对该点周围为''1''的元素作为参数调用BFS函数

class Solution {
    public int numIslands(char[][] grid) {
        if(grid==null || grid.length==0)return 0;
        int count=0;
        for(int i=0;i<grid.length;i++){
            for(int j=0;j<grid[0].length;j++){
                if(grid[i][j]=='1'){
                    count++;
                    BFS(grid,i,j);
                }
            }
        }
        return count;
    }

    public void BFS(char[][] grid,int x,int y){
    grid[x][y] = '0';
    int n = grid.length;
    int m = grid[0].length;
    Queue<Integer> queue = new LinkedList<>();
    int code = x * m + y;
    queue.add(code);
    while (!queue.isEmpty()) {
        code = queue.poll();
        int i = code / m;
        int j = code % m;
        if (i > 0 && grid[i - 1][j] == '1') {
            grid[i - 1][j] = '0';
            queue.add((i - 1) * m + j);
        }
        if (i < n - 1 && grid[i + 1][j] == '1') {//下
            grid[i + 1][j] = '0';
            queue.add((i + 1) * m + j);
        }
        if (j > 0 && grid[i][j - 1] == '1') { //左
            grid[i][j - 1] = '0';
            queue.add(i * m + j - 1);
        }
        if (j < m - 1 && grid[i][j + 1] == '1') {//右
            grid[i][j + 1] = '0';
            queue.add(i * m + j + 1);
        }
    }
    }
}

?DFS:首先利用双循环遍历矩阵每个元素，若有元素为"1",则岛屿个数+1，并将该点作为参数调用DFS函数。

DFS函数：将传入点变为''0''。将该元素的四个点作为参数递归调用DFS。

class Solution {
    public int numIslands(char[][] grid) {
        if(grid.length==0 || grid==null){
            return 0;
        }
        int count=0;
        for(int i=0;i<grid.length;i++){
            for(int j=0;j<grid[0].length;j++){
                if(grid[i][j]=='1'){
                    count++;
                    dfs(grid,i,j);
                }
            }
        }
        return count;
    }
    public void dfs(char[][] grid,int i,int j){
        if(i<0 || i>grid.length-1 || j>grid[0].length-1 || j<0  || grid[i][j]=='0'){
            return;
        }
        grid[i][j]='0';
        dfs(grid,i-1,j);
        dfs(grid,i+1,j);
        dfs(grid,i,j+1);
        dfs(grid,i,j-1);
    }

}