图的基本概念和基本术语
-
图的概念
图G是由V,E两个集合组成的,G=(V,E),V是结点,E是边。
有向图:就是由箭头指方向的。
无向图:就是没有方向的
-
图的基本术语
子图:G=(V,E),G2=(V2,E2), V2是V的真子集同时E2也是E的真子集,那么G2为G的子图
无向完全图:N个顶点的无向图,具有n(n-1)/2条边。 有向完全图:N个顶点的有向图,具有n(n-1)条边。
稀疏图:边的条数|E|远小于|V|2(顶点)。稠密图:边的条数|E|接近|V|2。
权:每一天边可以给予一定的数值。表示一个点到另外一个点的距离或者耗费。 网:带权的图
邻接点:被同一条线连接的两个点。
度:无向图的度主要是看这个顶点被几条线连着,有向图的度=入度+出度。入度:有一个箭头指向一个顶点,那这个顶点的入度就为1(这个是进来)。
出度:某一个结点的一个线指向某一个顶点(大致意思就是出去)。
路径长度:一个顶点到另外一个顶点所走过的的边或者弧。 回路:1-2-1,顶点1出发,经过2,然后再回到1. 简单回路:从顶点出发,再回来,不能经过重复的路径或者顶点。
连通:点和点之间有路径,就是连通的。连通图:一个图中任意两个点都是可以到达的。
连通分量:连通图只有一个连通分量,就是他自己。非连通图连接分量就是子图。
强连接图:顶点和顶点之前能够之间到达,不需经过其他顶点。强连通分量:不能之间连的顶点,一般就是强连通分子。
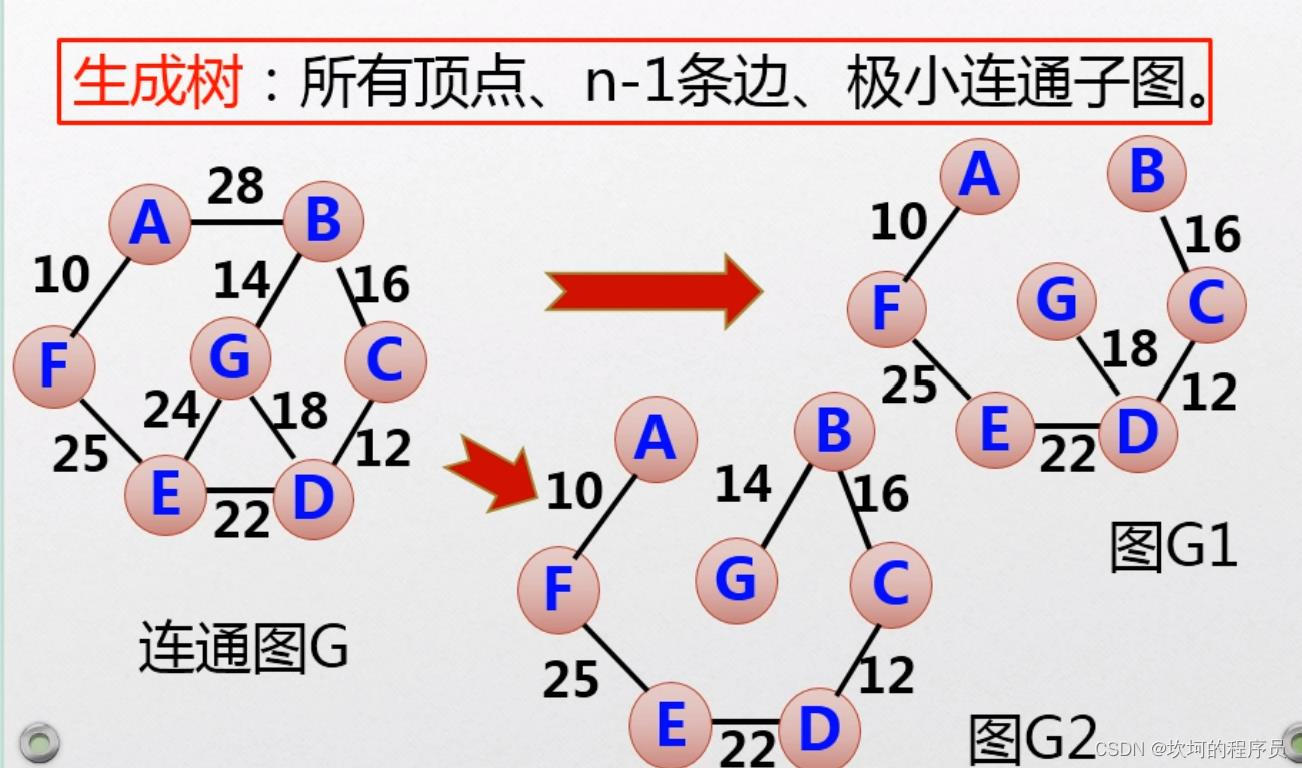
连通图的生成树:由极小连通子图构成,但边只有N-1条边

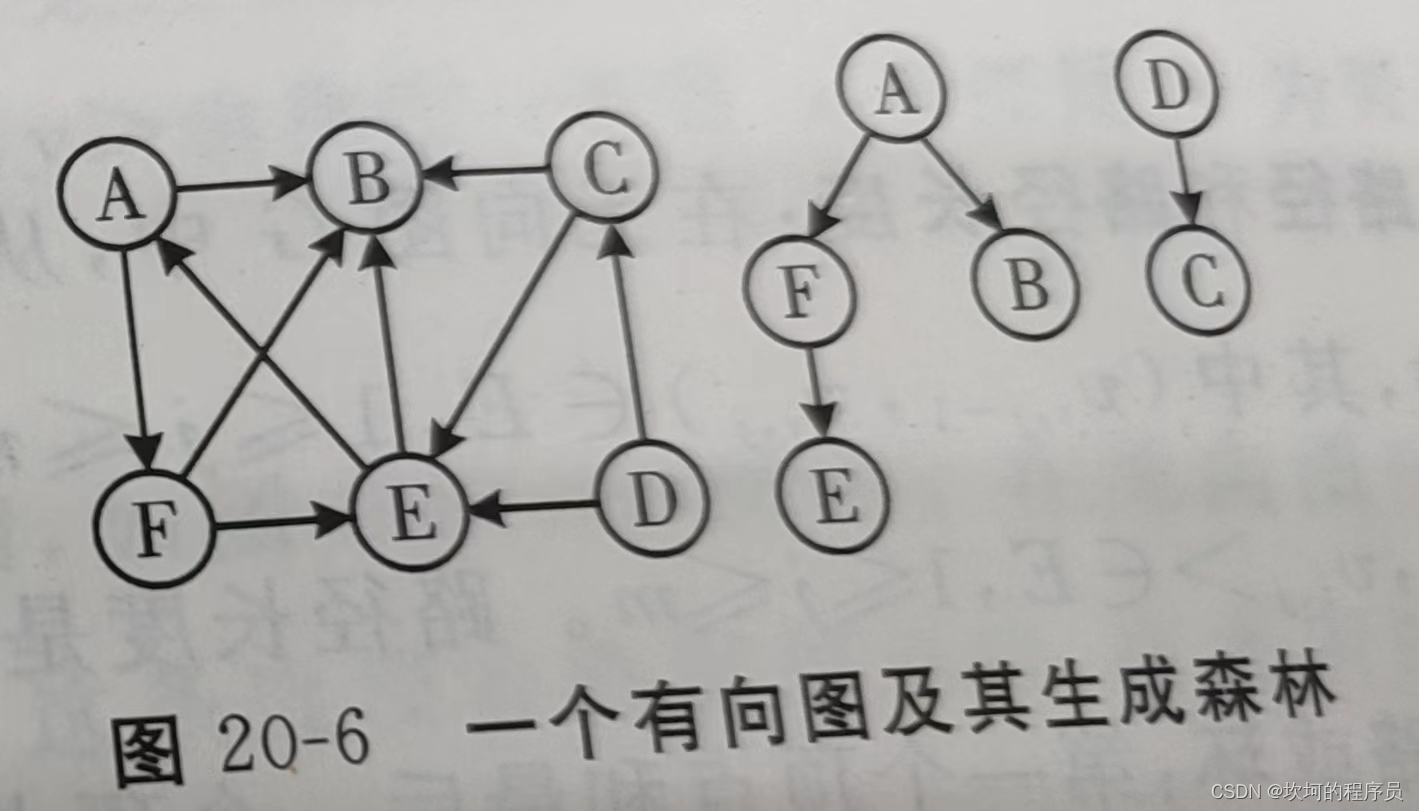
有向树和生成森林:
有向树:有一个顶点为0,其余顶点的入度为1的有向图为有向树。
森林是由若干课有向树构成。
图的存储结构
-
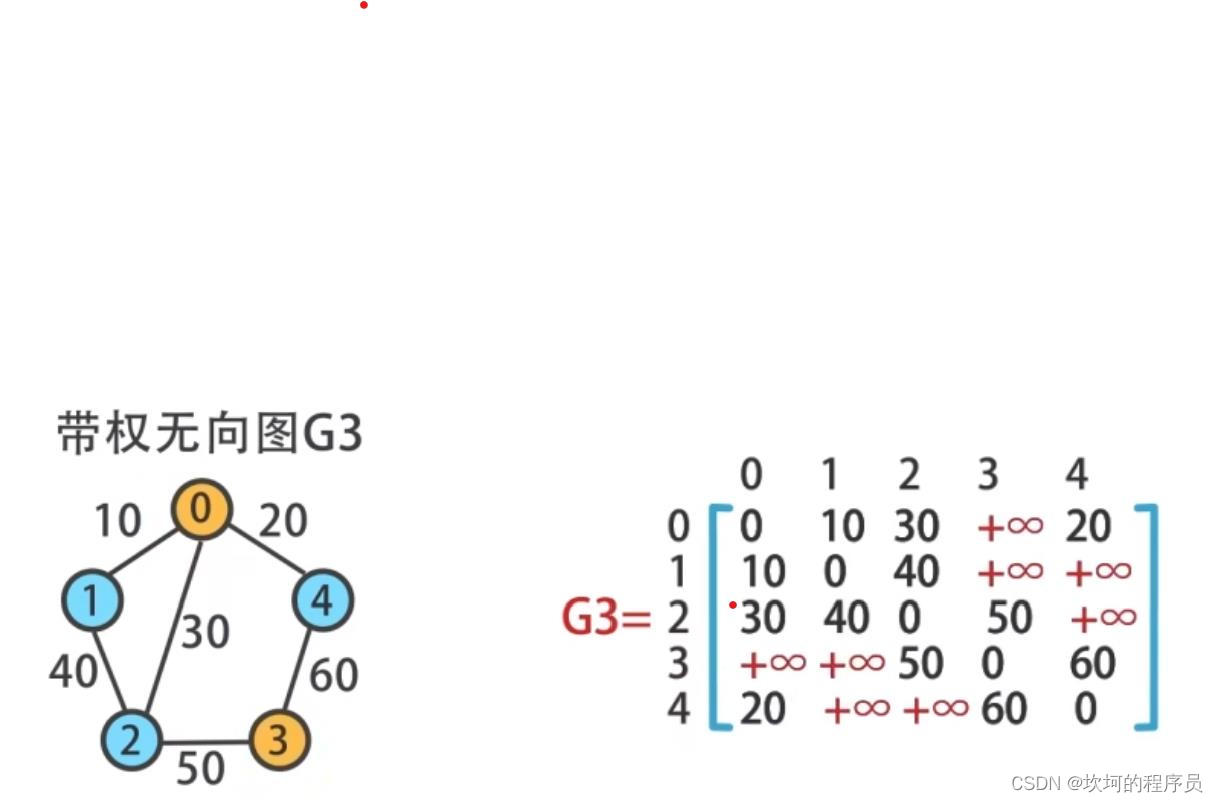
邻接矩阵
顶点之间可以连通的就是1,不能就是1,或者本身连本身也是0
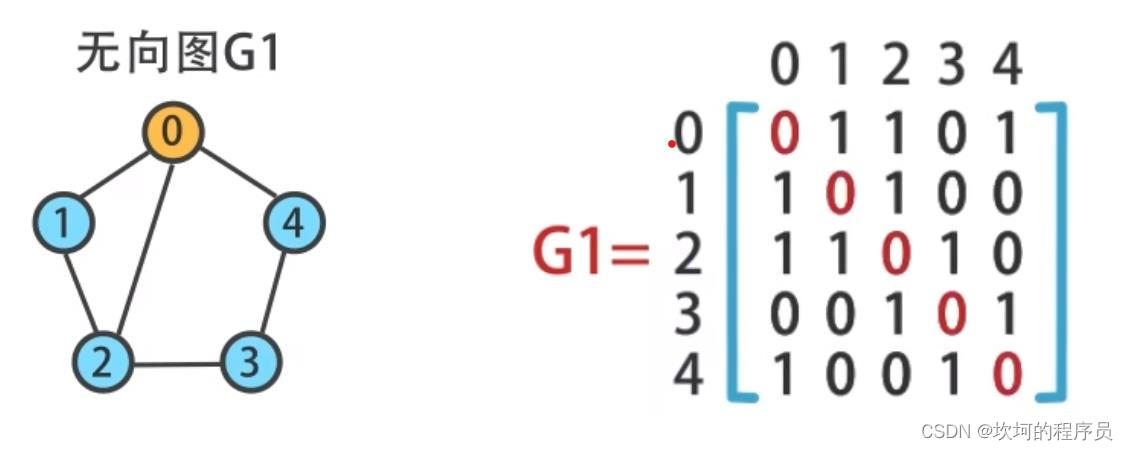
0到0,表示距离为0,不能到达的就是无穷大。
-
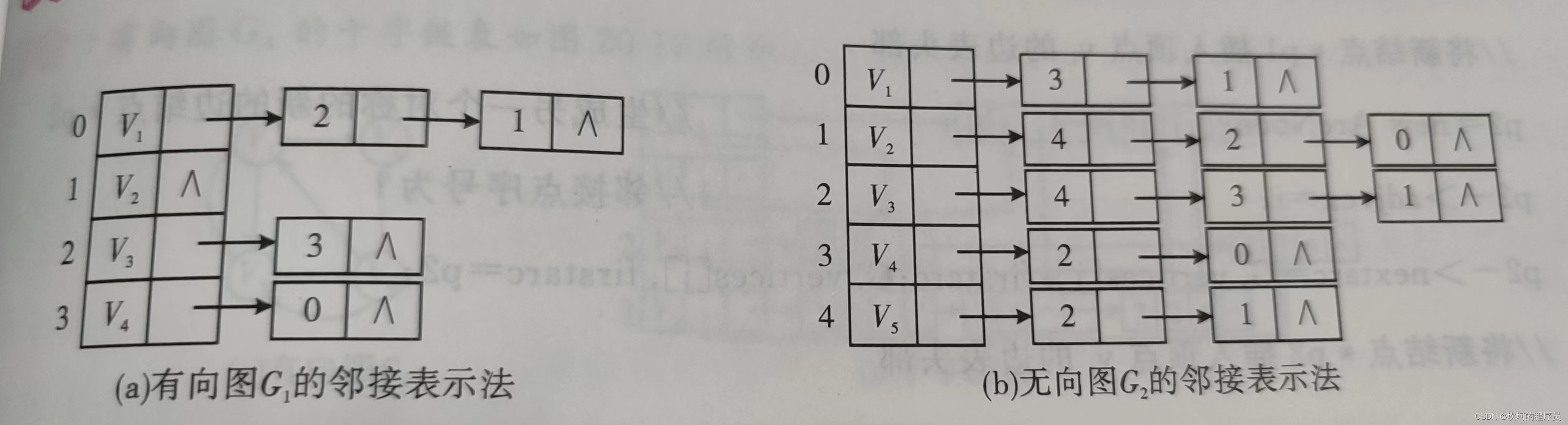
邻接表
邻接表是图的链式表示方法,由表头结点表和边表组成。
表头结点:由数据域和链域组成。
边表:由邻接点域、数据域、链域组成
- 邻接表的优缺点:
优点:
便于增加和删除。便于统计边的数。空间效率高(O(n+e))n:代表多少顶点,e:表示多少个边表结点。
缺点:不便判断顶点之间是否有边。不便计算有向图各个顶点的度
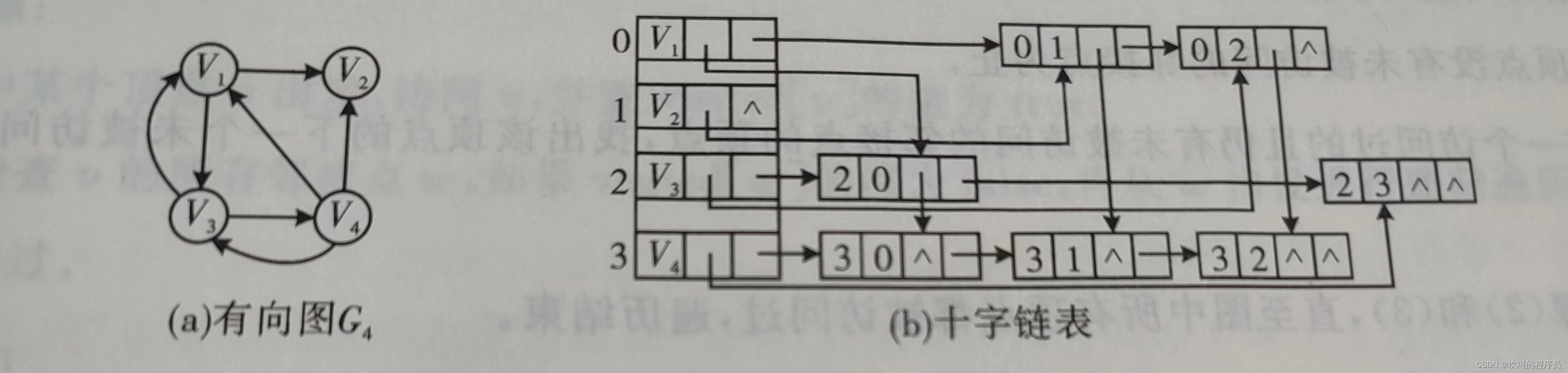
十字链表
十字链表通过头尾域和两个链域、info域(弧的信息)
链域:一个是指向弧头相同的下一个弧,一个是指向弧尾相同的下一个弧。
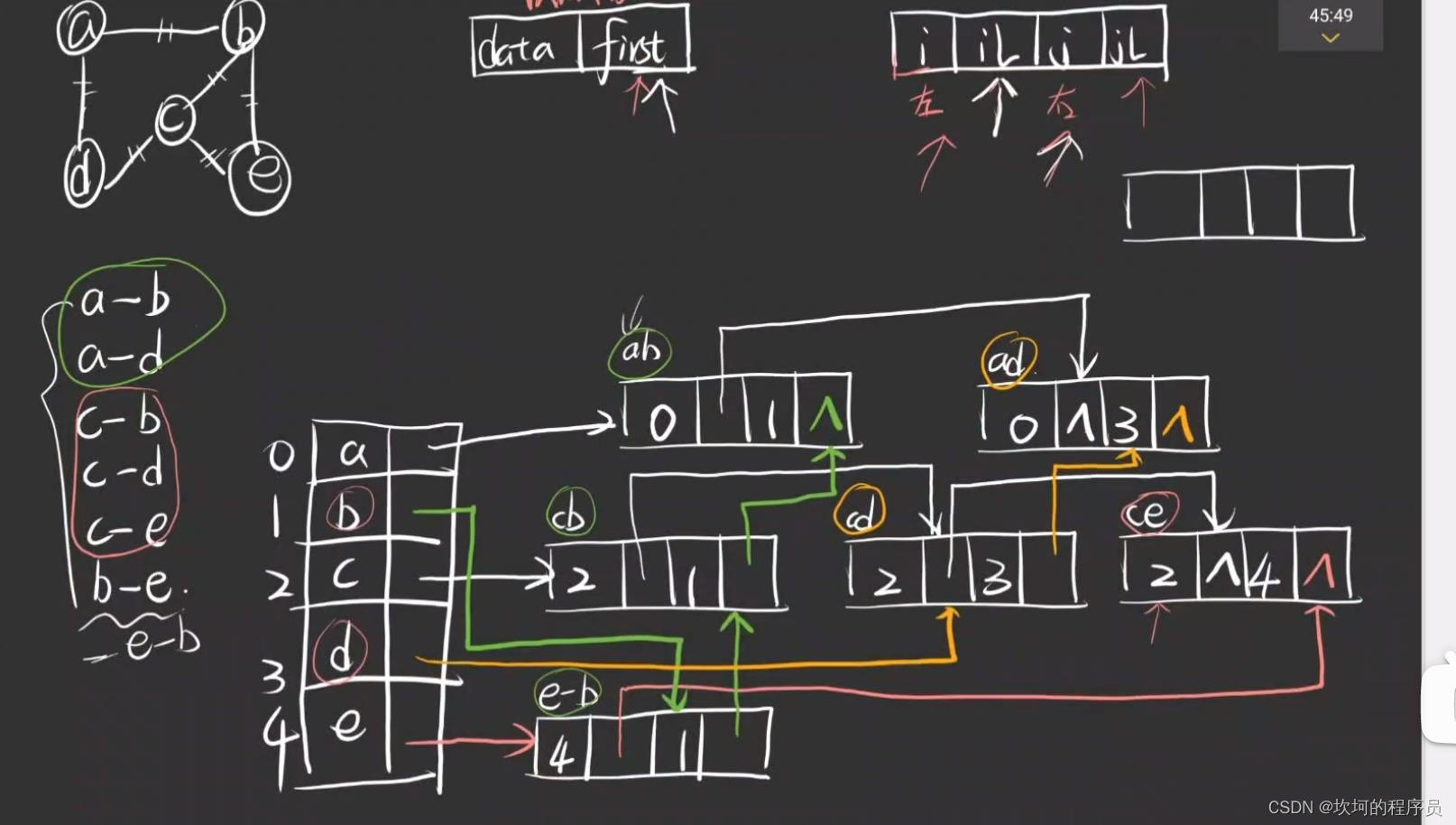
邻接多重表
有头节点和尾结点,还有相同头结点的链域,相同尾结点的链域
图的遍历
-
深度优先算法
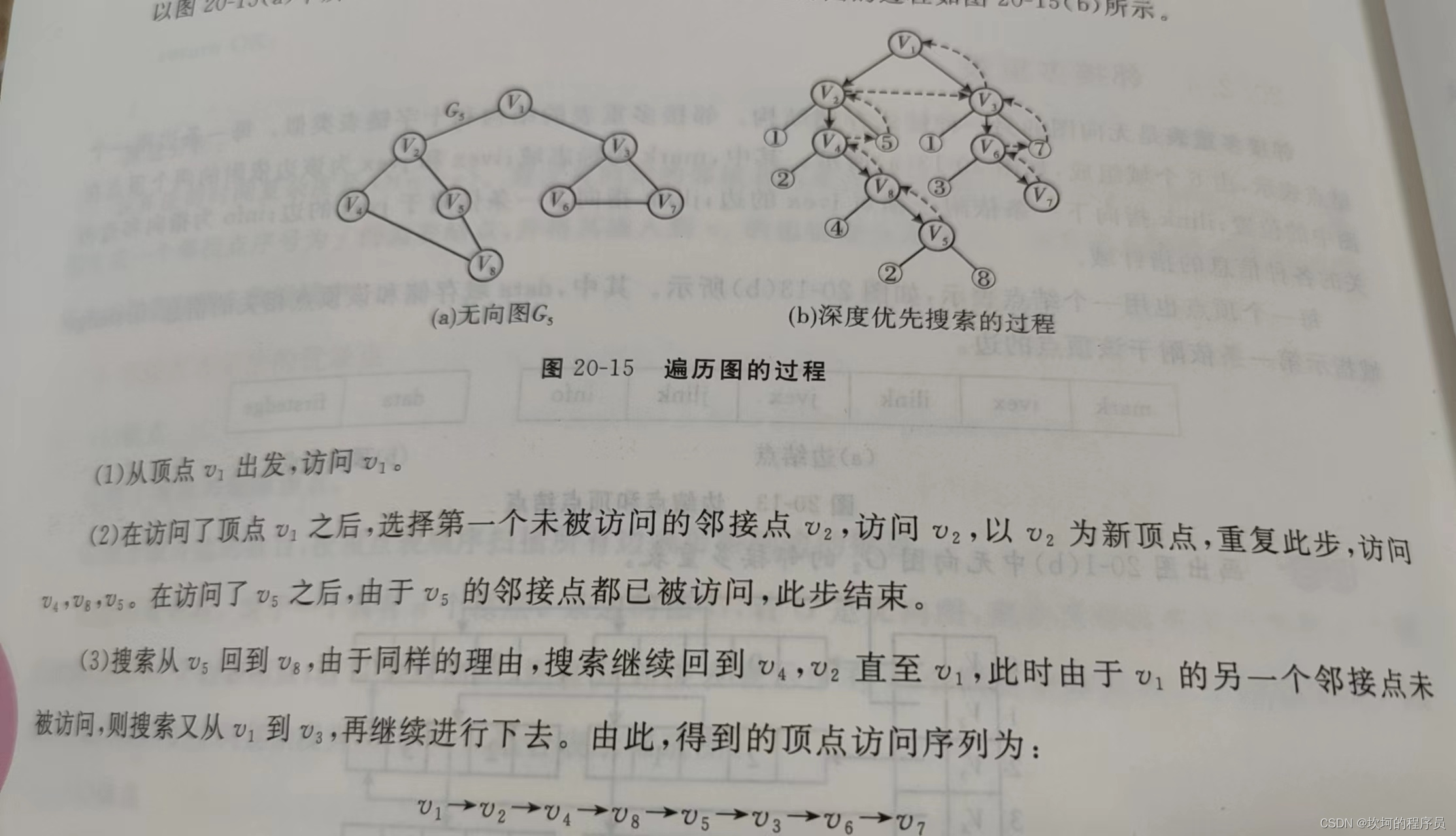
深度优先搜索:
1.选择一个顶点,然后找一个没有被访问的邻结点,访问该结点,然后一直重复,直到访问过的结点没有未被访问的邻结点。
2.某个结点的邻结点都被访问完了,则返回上一个邻结点,直到找到没有被访问的结点。
3.如果都访问完了,则遍历结束。
-
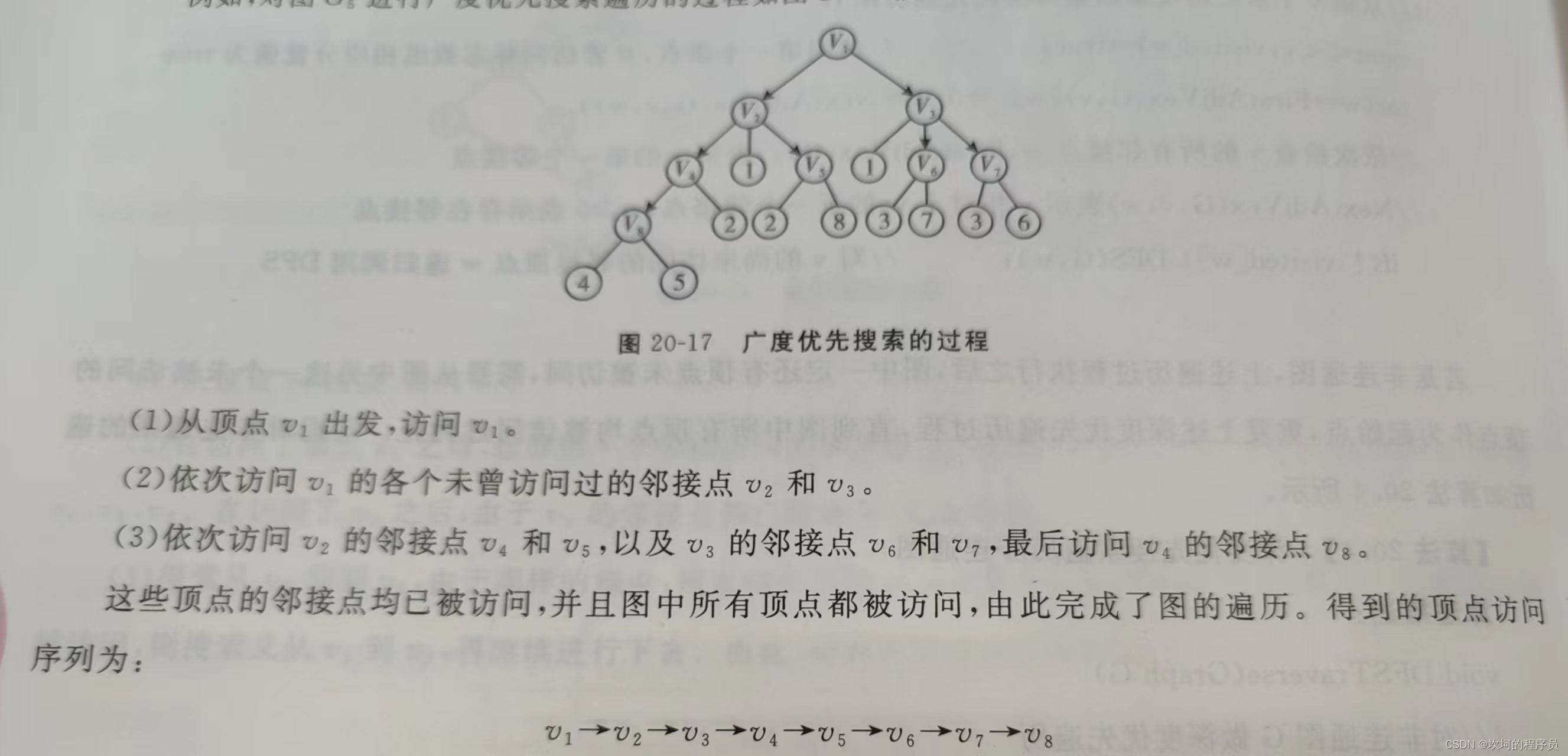
广度优先算法
1.从顶点出发,选择某一个邻结点(比如左边),然后在选择邻一个邻结点(比如右边)。
2.当选择的左子树的邻接点,那每次都会先遍历左边的邻接点。
3.遍历是一层一层的遍历
最小生成树
在一个连通图里,边最少的就是最小代价生成树,简称最小生成树。
-
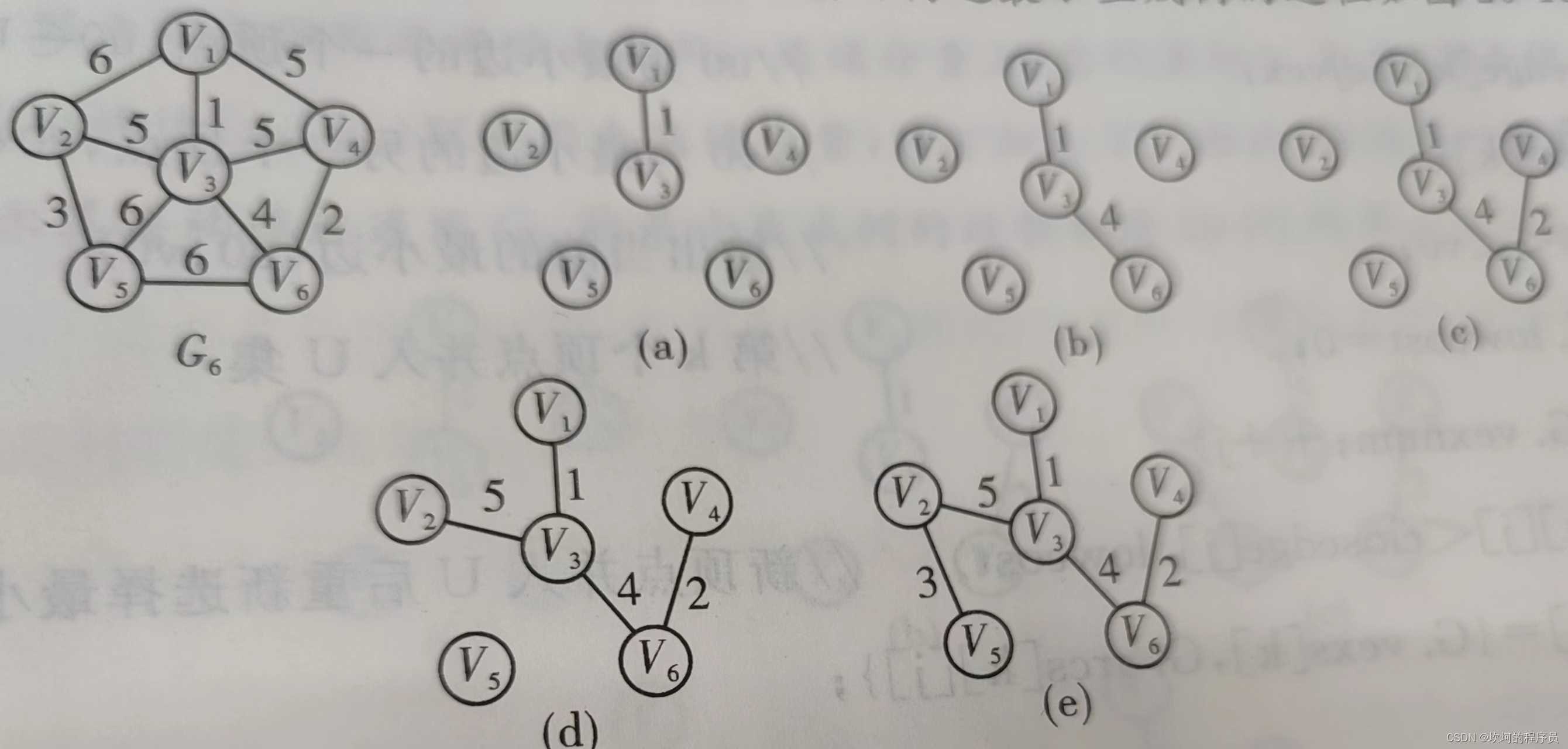
普利姆算法
过程:
1.选择一个顶点,然后顺着该顶点向下寻找权值小的顶点连起来,然后一直循环,直到连完。
2.如果还没有访问完,就没有邻结点可以连了,就返回上一个邻接点,直到找到可以连的结点。
3.所有结点都只可以连接一次,不能成环。
-
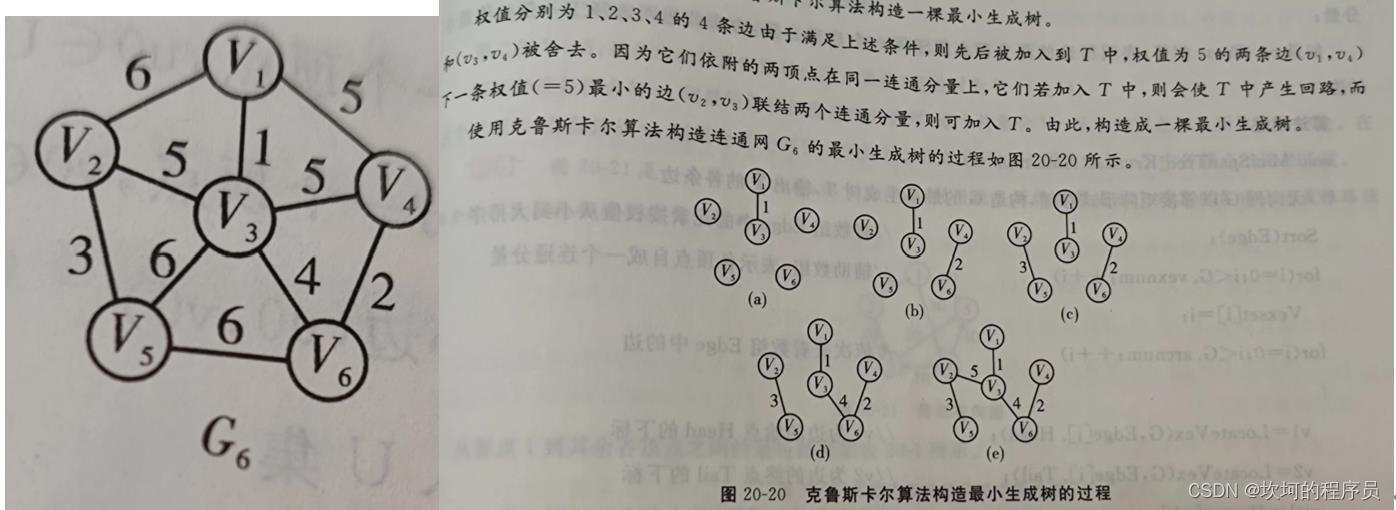
克鲁斯科尔算法
选择权值最小的边连起来,然后再找邻接点最小边的权值连起来,然后重复操作。(个人理解)
这个图先将合适的权值先连起来,不合适的之前丢掉。
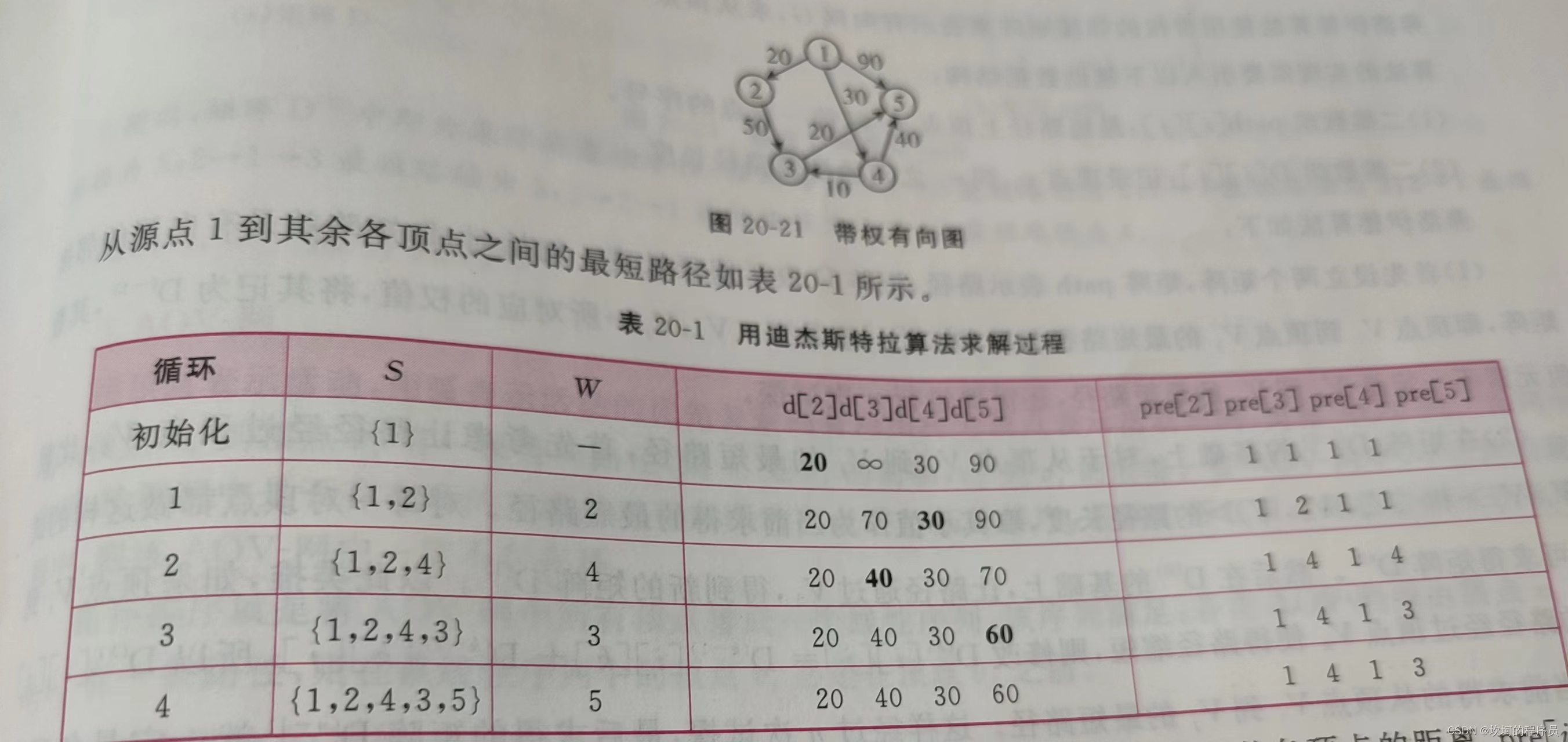
最短路径-迪杰斯特拉算法
算法步骤:就是将和选定顶点最近的路径连起来。
循环1:d[3]无穷大变成70,是因为1连接了2,就找到了1到2到3路径的长度为70.
循环2:d[3]从70变成40,是因为1连接了4,4的路径长度为30,第二小,所有1-4-3的路径长度为40
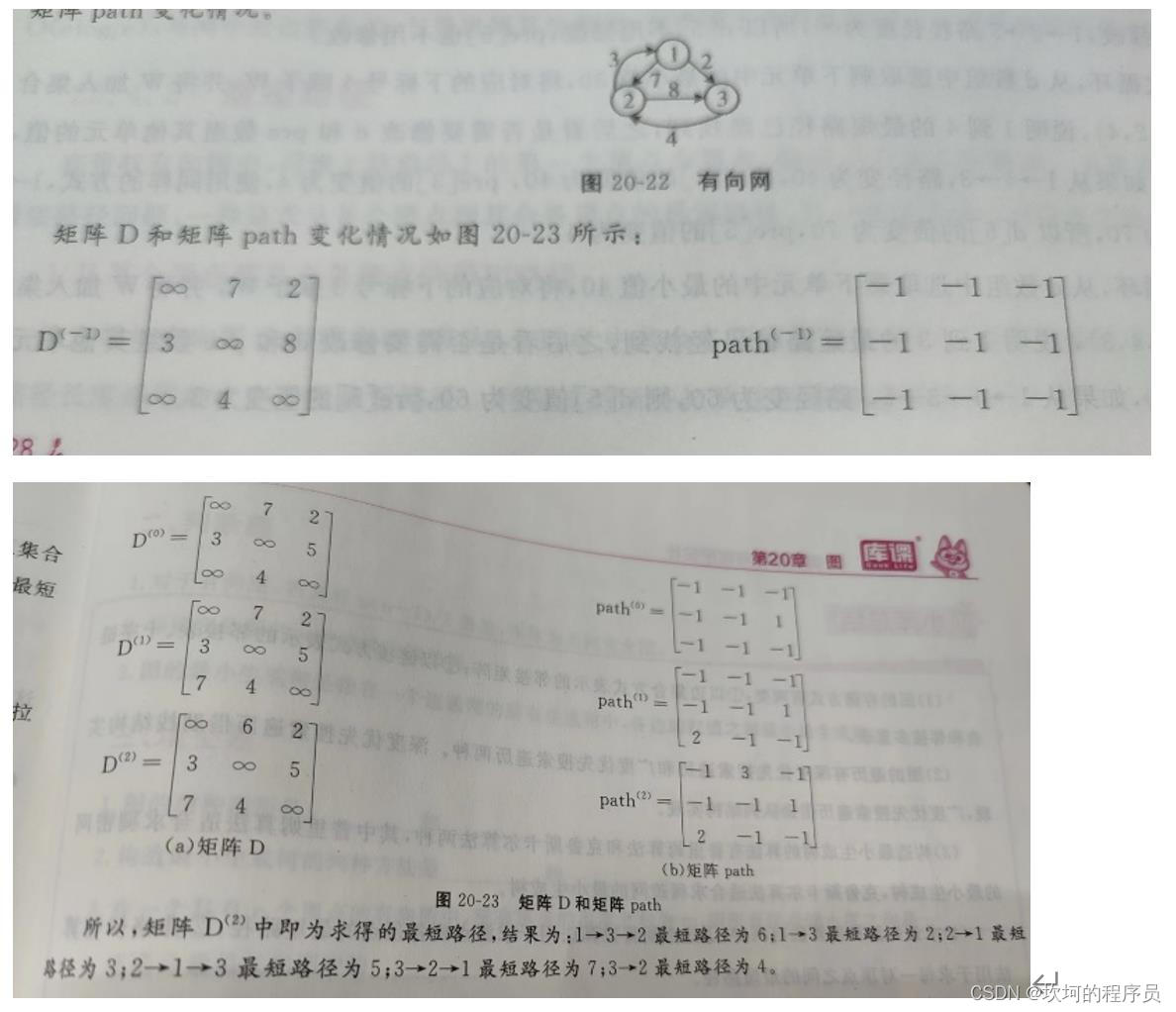
弗洛伊德算法
算法过程:
1.初始化一个路径矩阵和点和点之间是否能直达的矩阵。
2.从第一个顶点为中转站,一个顶点到另外一个顶点经过都要经过这个中转站,每个顶点都要当一次中转站,以此来测试哪个路径为最短。
矩阵的行和列的序标都是0,1,2(表示顶点1,2,3)
D^(-1):初始化两个矩阵
D^(0):以1作为中转站
D^(1):以2作为中转站
D^(2):以3作为中转站