[数据结构与算法]leetcode: 547. 省份数量

547. 省份数量

来源：力扣（LeetCode）

链接: https://leetcode.cn/problems/number-of-provinces/

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量。

示例 1：

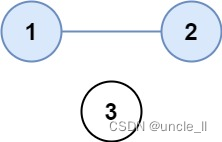
输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

示例 2：

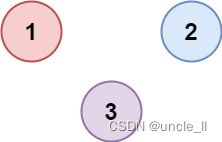
输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

提示：

• 1 <= n <= 200
• n == isConnected.length
• n == isConnected[i].length
• isConnected[i][j] 为 1 或 0
• isConnected[i][i] == 1
• isConnected[i][j] == isConnected[j][i]

解法

• DFS： 这个与岛屿问题有些类似，但是区别是间隔也可以是有联系的，isConnected[i][j]表示第i个城市与第j个城市有关联，另外关联是可以传递的，不像岛屿问题只看周边就行，因此这里dfs是以层 列为参数进行递归，矩阵的第i行表示第i个城市，第j列表示第j个城市，这里需要使用一个集合visited表示城市是否被访问过
• 并查集+联通区域：使用并查集添加城市，将有关联的城市联通起来，最后统计联通区域有多少即可

代码实现

DFS

python实现

class Solution:
    def findCircleNum(self, isConnected: List[List[int]]) -> int:
        cities = len(isConnected)
        count = 0
        visited = set()

        def dfs(i: int):
            for j in range(cities):
                if isConnected[i][j] == 1 and j not in visited:
                    visited.add(j)
                    dfs(j)
        
        for i in range(cities):
            if i not in visited:
                count += 1
                dfs(i)
        return count

c++实现

class Solution {
public:
    void dfs(vector<vector<int>>& isConnected, set<int>& visited, int cities, int i) {
        for (int j = 0; j < cities; j++) {
            if (isConnected[i][j] == 1 && visited.find(j) == visited.end()) {
                visited.insert(j);
                dfs(isConnected, visited, cities, j);
            }
        }
    }

    int findCircleNum(vector<vector<int>>& isConnected) {
        int cities = isConnected.size();
        set<int> visited;
        int count = 0;
        for (int i = 0; i < cities; i++) {
            if (visited.find(i) == visited.end()) {
                count++;
                dfs(isConnected, visited, cities, i);
            }
        }
        return count;
    }
};

复杂度分析

• 时间复杂度： $O(n^2)$
• 空间复杂度： $O(n)$

并查集

python实现

class UnionFind:
    def __init__(self):
        self.father = {}
        self.num_of_sets = 0
    
    def add(self, x):
        if x not in self.father:
            self.father[x] = None
            self.num_of_sets += 1
    
    def find(self, x):
        root = x
        while self.father[root] != None:
            root = self.father[root]
        
        while x != root:
            origin_father = self.father[x]
            self.father[x] = root
            x = origin_father
        return root

    def merge(self, x, y):
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x != root_y:
            self.father[root_x] = root_y
            self.num_of_sets -= 1

class Solution:
    def findCircleNum(self, isConnected: List[List[int]]) -> int:
        m = len(isConnected)
        uf = UnionFind()
        for i in range(m):
            uf.add(i)
            for j in range(i):
                if isConnected[i][j]:
                    uf.merge(i, j)
        return uf.num_of_sets

c++实现

class UnionFind:
    def __init__(self):
        self.father = {}
        self.num_of_sets = 0
    
    def add(self, x):
        if x not in self.father:
            self.father[x] = None
            self.num_of_sets += 1
    
    def find(self, x):
        root = x
        while self.father[root] != None:
            root = self.father[root]
        
        while x != root:
            origin_father = self.father[x]
            self.father[x] = root
            x = origin_father
        return root

    def merge(self, x, y):
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x != root_y:
            self.father[root_x] = root_y
            self.num_of_sets -= 1

class Solution:
    def findCircleNum(self, isConnected: List[List[int]]) -> int:
        m = len(isConnected)
        uf = UnionFind()
        for i in range(m):
            uf.add(i)
            for j in range(i):
                if isConnected[i][j]:
                    uf.merge(i, j)
        return uf.num_of_sets

复杂度分析

• 时间复杂度： $O(n^{2}logn)$
• 空间复杂度： $O(n)$

参考

• https://leetcode.cn/problems/number-of-provinces/solution/sheng-fen-shu-liang-by-leetcode-solution-eyk0/
• https://leetcode.cn/problems/number-of-provinces/solution/python-duo-tu-xiang-jie-bing-cha-ji-by-m-vjdr/
• https://leetcode.cn/problems/number-of-provinces/solution/dfs-bfs-bing-cha-ji-3-chong-fang-fa-ji-s-edkl/