[数据结构与算法] 【C++】哈希应用

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 【C++】哈希应用 -> 正文阅读

[数据结构与算法]【C++】哈希应用

文章目录

常见哈希函数

直接定制法
取关键字的某个线性函数为散列地址：Hash（Key）= A*Key + B 优点：简单、均匀缺点：需要事先
知道关键字的分布情况使用场景：适合查找比较小且连续的情况
除留余数法
设散列表中允许的地址数为m，取一个不大于m，但最接近或者等于m的质数p作为除数，按照哈希函
数：Hash(key) = key% p(p<=m),将关键码转换成哈希地址
平方取中法
假设关键字为1234，对它平方就是1522756，抽取中间的3位227作为哈希地址；再比如关键字为
4321，对它平方就是18671041，抽取中间的3位671(或710)作为哈希地址平方取中法比较适合：不知
道关键字的分布，而位数又不是很大的情况
折叠法
折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些)，然后将这几部分叠加
求和，并按散列表表长，取后几位作为散列地址。
折叠法适合事先不需要知道关键字的分布，适合关键字位数比较多的情况

以下是折叠法具体实现示意图：
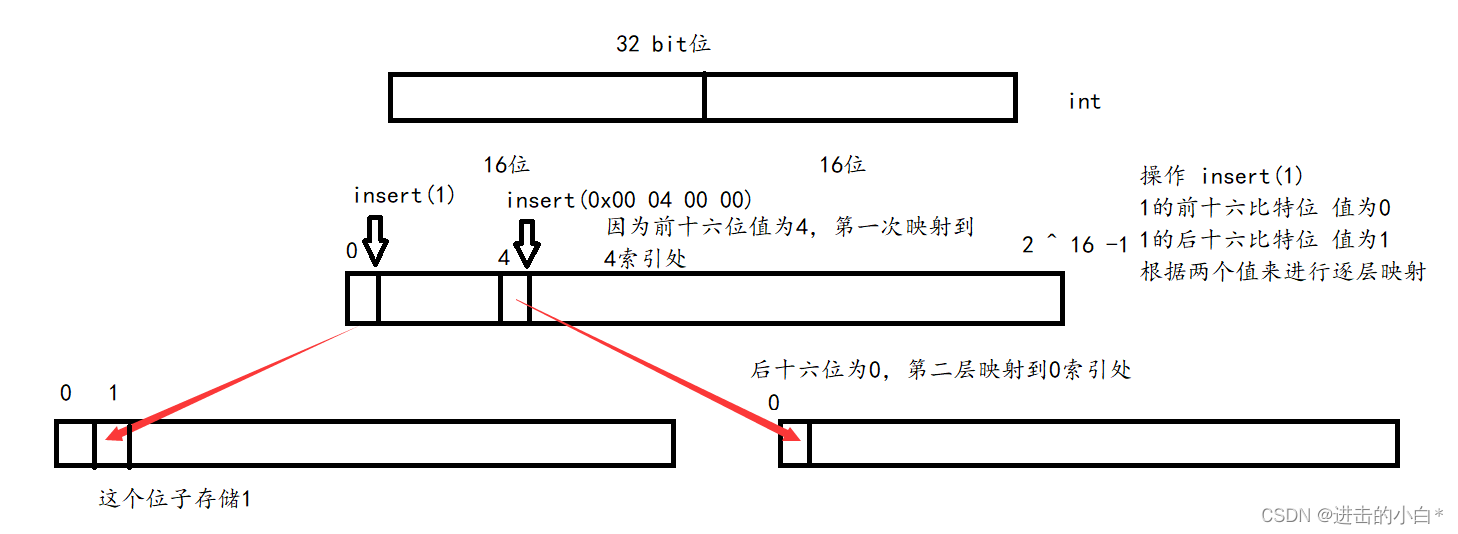
在这里插入图片描述
处理过的key是一个unsigned int ，我们使用位操作将其切分成几片，可以均匀也可以不均匀（图中是切割均匀的两片）。然后我们计算每一段的大小，因为16个比特位表示0 ~ 2 ^16 -1 的值，所以我们就开这么多的空间，然后通过前16位对应的值映射到第一个开辟的数组上，然后通过第一个映射位置再开一个vector与其相连，然后通过后十六位的值来判断第二层的索引值。

优化方法：像图示方法我们牺牲了较大的空间，因为2 ^ 16比较大，开两层对空间的消耗较大。我们可以通过增加对key切割次树，从而增加映射的次数，这样可以减少空间的大小。（比如平均切分成4段，那么每一层只需要开 2 ^ 8 = 256 个空间）每一个值的存储最多会消耗 2 ^ 8 * 4 = 1024 个空间。但是增加切割次数在查找时也必须要增加查找的次数，切割两次找两次，切割四次找四次。我们需要根据应用场景灵活的选择切割方式

随机数法
选择一个随机函数，取关键字的随机函数值为它的哈希地址，即H(key) = random(key),其中random为随机数函数。
通常应用于关键字长度不等时采用此法

好的哈希函数可以尽量减少哈希冲突的发生的概率，但是不能完全防止哈希冲突

位图的应用

在这里插入图片描述
概念：采用直接定值法，只能适用于key为整形的情况
底层实现：通过开辟一个vector，将每一个比特位看成一个数字，若插入结点的key = 0，则将第一个比特位设置成零。整形的大小接近是四十二亿九千万个字节，也就相当于4G，若每个整形占用一个比特位那么需要开辟接近 4G / 8 = 0.5G的空间。那么我们就可以通过最大为0.5G位图来存储key

重要接口：
set :给定一个位置，将这个比特位设置为1
reset：给定一个位置，将这个比特位设置为0
test：给定一个位置，若这个位置值为1 则返回true 为0 则返回false
位图的应用

快速查找莫数据是否在集合中
排序
求交集
操作系统堆磁盘块进行标记
海量数据处理

位图的模拟实现

#pragma once 
#include <iostream>
#include <vector>
using namespace std;

template<size_t N>
class my_bitset
{
public:
    my_bitset() { v.resize(N / 8 + 1, 0); }
    my_bitset& set(size_t pos);
    my_bitset& reset(size_t pos);
    bool test(size_t pos);
    size_t size();
private:
    vector<char> v;
};

template<size_t N>
my_bitset<N>& my_bitset<N>::set(size_t pos)
{
    size_t  index = pos / 8;
    size_t bit_index = pos % 8;
    v[index] = v[index] | (1 << bit_index);
    return *this;
}

template<size_t N>
my_bitset<N>& my_bitset<N>::reset(size_t pos)
{
    size_t index = pos / 8;
    size_t bit_index = pos % 8;
    v[index] = v[index] & (~(1 << bit_index));
    return *this;
}

template<size_t N>
bool my_bitset<N>::test(size_t pos)
{
    size_t index = pos / 8;
    size_t bit_index = pos % 8;
    return (bool)(v[index] & (1 << bit_index));
}

void my_bitset_test()
{
    my_bitset<1000> bs;
    bs.set(1);
    bs.set(11);
    bs.set(15);
    cout << bs.test(11) << endl;
    cout << bs.test(16) << endl;
}

位图具有一定的局限性，位图只能传递整形进行操作，我们需要将我们想要操作的类型经过某种处理转化为整形才可以传入。

布隆过滤器

bloon filter(布隆过滤器)：底层为位图，为大量数据的存储节省空间，其可以降低冲突的概率，但不能完全避免冲突。所以布隆过滤器经常用于处理大量访问等情况，在经过过滤器后还要进行进一步处理

布隆过滤器的实现原理（以key类型为string举例）
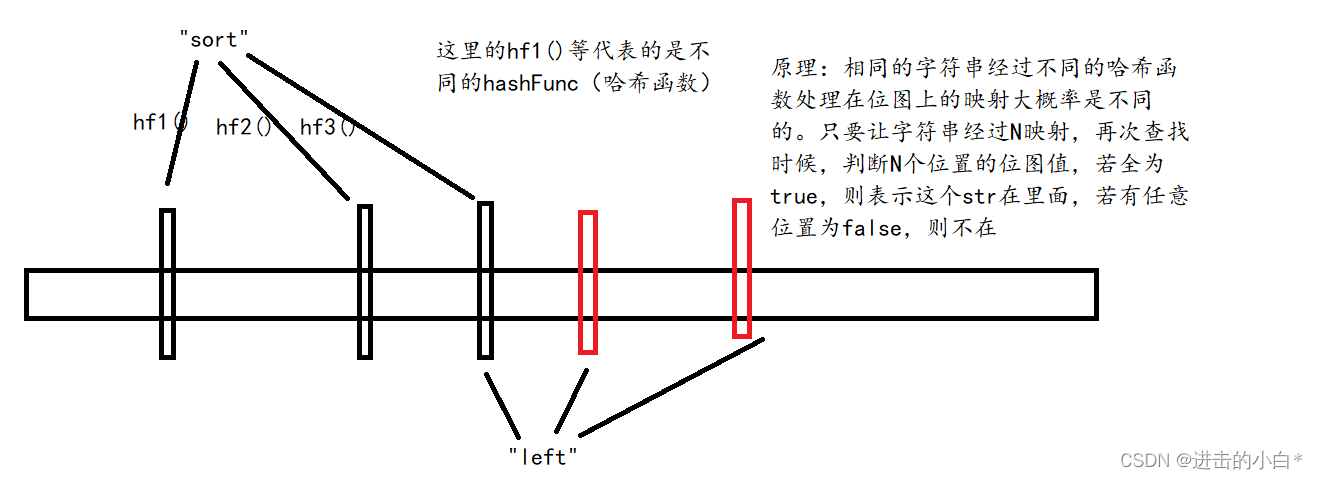
在这里插入图片描述
如图，对于每一个key（string）对其使用三次哈希函数，根据三次映射结果位图上三个位置设置为1。
布隆过滤器判断存在时要求，这个key的三个映射的区域都为1，才返回true。像图上的left和sort若它们某一个哈希函数将两个字符串映射到同一个地方时，那么无法区分sort在而left不在，sort不再left在，两者都在的情况。而若三次映射，则映射位置全部在一起的概率就会小很多。如图示情况就可以避免两者的判断失误。
单次映射需要开较大的空间以降低哈希冲突的效率，布隆过滤器的价值就在节省空间降低冲突概率。但是任然会存在冲突，在布隆过滤器中若不在则必定不在，在则可能在

布隆过滤器模拟实现

框架解析

template<size_t N, size_t X,
  class HashFunc1,
  class HashFunc2,
  class HashFunc3>
class bloon_filter
{
  public:
    bloon_filter& set(const string&  str);
    bool test(const string& str);
  private:
    bitset<N * X> bs;
};

模板参数：
N：准备存储的数据个数
X：控制位图的长度是N的倍数
HashFunc + 数字：哈希函数
成员函数
set：将哈希函数处理过的key映射到位图上
test：检验key经过哈希函数处理过后映射在位图的位置的值，全为一返回true 否则返回false

成员变量
最小可以存储N*X个比特位的位图

struct BKDRHash
{
	size_t operator()(const string& s)
	{
		// BKDR
		size_t value = 0;
		for (auto ch : s)
		{
			value *= 31;
			value += ch;
		}
		return value;
	}
};

struct APHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 0;
		for (size_t i = 0; i < s.size(); i++)
		{
			if ((i & 1) == 0)
			{
				hash ^= ((hash << 7) ^ s[i] ^ (hash >> 3));
			}
			else
			{
				hash ^= (~((hash << 11) ^ s[i] ^ (hash >> 5)));
			}
		}
		return hash;
	}
};

struct DJBHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 5381;
		for (auto ch : s)
		{
			hash += (hash << 5) + ch;
		}
		return hash;
	}
};


template<size_t N, size_t X,
  class HashFunc1,
  class HashFunc2,
  class HashFunc3>
class bloon_filter
{
  public:
    bloon_filter& set(const string&  str)
    {
      HashFunc1 h1;
      HashFunc2 h2;
      HashFunc3 h3;
      size_t len = X * N;
      size_t index1 = h1(str) % len; //映射关键值1
      size_t index2 = h2(str) % len; //映射关键值2
      size_t index3 = h3(str) % len; //映射关键值3
      bs.set(index1); //将三个映射关键值在位图中的位置设置为1
      bs.set(index2);
      bs.set(index3);
      
      return *this;
    }

    bool test(const string& str)
    {
      HashFunc1 h1;
      HashFunc2 h2;
      HashFunc3 h3;
      size_t len = X * N;
      size_t index1 = h1(str) % len;
      size_t index2 = h2(str) % len;
      size_t index3 = h3(str) % len;
      return bs.test(index1)    //三个映射位置都为1则返回true 否则返回false
        &&   bs.test(index2)
        &&   bs.test(index3);
    }
  private:
    bitset<N * X> bs;
};

布隆过滤器性能测试

设计思路：
base：将一组相似的字符串直接映射到位图上和经过布隆过滤器映射到位图上
将一组和base相似但是不完全相同的字符串经过处理分别在位图和布隆过滤器中查找，记录存在次数（即误判次数）
将一组和base不同也不相似的字符串处理分别放在布隆过滤器和位图上查找，记录存在次数（即误判次数）
因为第二组和第三组数据和第一组一定不同，查找第二或第三组理论上应该是返回不存在的，但是因为存在哈希冲突，会产生误判，所以我们可以根据误判的次数来判断性能

#include "my_filter.h"
#define N 1000
#define X 10

void test1()
{
  bloon_filter<N, X, BKDRHash, APHash, DJBHash> bf;
  //和布隆过滤器相同大小的位图
  bitset<N * X> bs;
  vector<string> v1;
  vector<string> v2;
  vector<string> v3;
  //v1存储N个字符串，它们都很相似，只是后缀不一样
  for (int i = 0; i < N; i++)
  {
    string base = "https://gitee.com/bithange/class_code/blob/master/class";
    string end = base + to_string(1234 + i);
    v1.push_back(end);
  }
  //v2存储N个字符串，它们和v1的也很相似，后缀也不一样
  for (int i = 0; i < N; i++)
  {
    string base = "https://gitee.com/bithange/class_code/blob/master/class";
    string end = base + to_string(5678 + i);
    v2.push_back(end);
  }

  //v3存储N个字符串， 它们和v1内字符串不同
  for (int i = 0; i < N; i++)
  {
    string base = "https://fanyi.baidu.com/translate?aldtype=16047&query";
    string end = base + to_string(5678 + i);
    v3.push_back(end);
  }
  //使用单个哈希函数
  BKDRHash ap; 
  //将v1每一个字符串标记进入位图和布隆过滤器
  for (auto str : v1)
  {
    bf.set(str);
    bs.set(ap(str) % (N*X));
  }

  size_t n1 = 0; //存储布隆过滤器中误判次数（使用相似key）
  size_t n3 = 0; //存储直接使用位图误判次数（使用相似key）
  for (auto str: v2)
  {
    if (bf.test(str))
      n1++;
    if (bs.test(ap(str) % (N*X)))
      n3++;
  }

  size_t n2 = 0; //存储布隆过滤器中误判次数（使用不相似key）
  size_t n4 = 0; //存储直接使用位图误判次数（使用不相似key）
  for (auto str : v3)
  {
    if (bf.test(str))
      n2++;
    if (bs.test(ap(str) % (N*X)))
      n4++;
  }


  cout << "布隆过滤器相似误判率为" << (double)n1 / N << endl;
  cout << "布隆过滤器非相似误判率为" << (double)n2 / N << endl;
  cout << "直接位图相似误判率为" << (double)n3 / N << endl;
  cout << "直接位图非相似误判率为" << (double)n4 / N << endl;
}

int main()
{
  test1();
  return 0;
}

测试结果

[clx@VM-20-6-centos bloon_filter]$ ./test
N=1000 : X=5
布隆过滤器相似误判率为0.073
布隆过滤器非相似误判率为0.095
直接位图相似误判率为0.323
直接位图非相似误判率为0.021

[clx@VM-20-6-centos bloon_filter]$ ./test
N=1000 : X=10
布隆过滤器相似误判率为0.008
布隆过滤器非相似误判率为0.009
直接位图相似误判率为0.293
直接位图非相似误判率为0.021

[clx@VM-20-6-centos bloon_filter]$ ./test
N=1000 : X=15
布隆过滤器相似误判率为0
布隆过滤器非相似误判率为0
直接位图相似误判率为0.293
直接位图非相似误判率为0.021

我们可以观察到当X越小，误判率越高，说明空间大小和误判率关系还是非常密切的
当空间大小相同的情况下，布隆过滤器的误判率都远小于直接使用单一哈希函数进行位图判断
节省空间减少哈希冲突，这就是布隆过滤器的价值所在

布隆过滤器的优缺点

布隆过滤器的优势
1.查询元素存在的时间复杂度为O(K)，K为哈希函数的个数（一般都很小，并且与数据量无关），查找效率虽比位图稍高，但是胜在节省大量空间。
2.哈希函数相互之间没有联系，方便硬件并行运算
3.布隆过滤器不需要存储元素本身，只需要存储key对应的哈希关键之，在某些保密要求严格的场所存在巨大优势
4.若允许少量误判的情况下，布隆过滤器比其他数据结构拥有很大的空间优势
5.数据量很大时，布隆过滤器可以表示全集
6.布隆过滤器可以对同一散列集进行交并差运算
布隆过滤器的劣势
1.存在误判，可能会出现假阳性的情况
解决方法：将过滤后的所有阳性情况取出组成其他数据结构，进行搜索排除
2.不能获取元素本身
3.布隆过滤器一般不支持删除
4.如果采用计数方式删除，可能存在计数回绕问题

此处的4讲的就是布隆过滤器的删除问题，计数法是删除的较常用手段。意为开更大的空间，让每一个key的哈希关键值占有一小块比特位，每个计数位增加一次就在这块比特位上++，比如八个比特位就可以表示这个哈希关键值存在0 ~ 255次重复的情况，删除则K个key对应的关键值–。但是若有一个位置超过255次，则将重新变为0，这就是计数回绕

计数回绕虽然解决了布隆过滤器的删除，但是其的代价有点大。每个位置需要更多的空间，性价比很低，所以布隆过滤器一般不支持删除

哈希切割

举例讲解：
给一个超过100G大小的IP file, IP file中存着IP地址, 设计算法找到出现次数最多的IP地址？如何找到IP file中 top K的IP

1.可以将100G大小的文件分成2000份，一份按理来说约等于50MB
2.对每一个IP地址经哈希函数后%2000，这样100G文件中的IP就被我们分到了100G的文件中。因为相同的IP进行哈希处理后映射到的文件肯定是相同的。
3.对每个小文件IP进行处理，可以建立map来存储pair<IP, int> 前一个参数存储IP，后一个参数计数，就可以得到每一个小文件中出现次数最多的IP地址，两千个文件则有两千个相对最大，取出其中最大的就是100G文件中最大的了
以上即是哈希切割的思路