[数据结构与算法]【力扣刷题】Day24——回溯专题

回溯专题到这就暂时完结啦，后续再多扩展刷题吧，上一篇文章：【力扣刷题】Day23——回溯专题_塔塔开!!!的博客-CSDN博客

四、排列问题

11. 全排列

题目链接：全排列

思路：模板题，dfs实现排列型枚举

Code

class Solution {
    int N = 25;
    int n;
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    boolean[] st = new boolean[N];
    public List<List<Integer>> permute(int[] nums) {
        n = nums.length;
        for(int i = 0; i < n; i ++) nums[i] += 10;// 防止数组下标为负数
        dfs(nums, 0);
        return res;
    }
    public void dfs(int[] nums, int u){
        if(u == n){
            res.add(new ArrayList(path));
            return ;
        }
        // 枚举每一种可能
        for(int i = 0; i < n; i ++){
            if(!st[nums[i]]){// 如果是这样子判断的话，nums[i]可能为负数，但是数组下标是不能为负的，为此要扩大
                st[nums[i]] = true;
                path.add(nums[i] - 10);
                dfs(nums, u + 1);
                st[nums[i]] = false;
                path.remove(path.size() - 1);// 回溯
            }
        }
    }
}

另一种写法（该位置上的数，用位置来判断是否选过）

Code

class Solution {
    int N = 25;
    int n;
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    boolean[] st = new boolean[N];
    public List<List<Integer>> permute(int[] nums) {
        n = nums.length;
        dfs(nums, 0);
        return res;
    }
    public void dfs(int[] nums, int u){
        if(u == n){
            res.add(new ArrayList(path));
            return ;
        }
        // 枚举每一种可能
        for(int i = 0; i < n; i ++){
            if(!st[i]){
                st[i] = true;
                path.add(nums[i]);
                dfs(nums, u + 1);
                st[i] = false;
                path.remove(path.size() - 1);
            }
        }
    }
}

12. 全排列 II

题目链接：47. 全排列 II - 力扣（LeetCode）

排列I枚举的话就会出现重复集合：

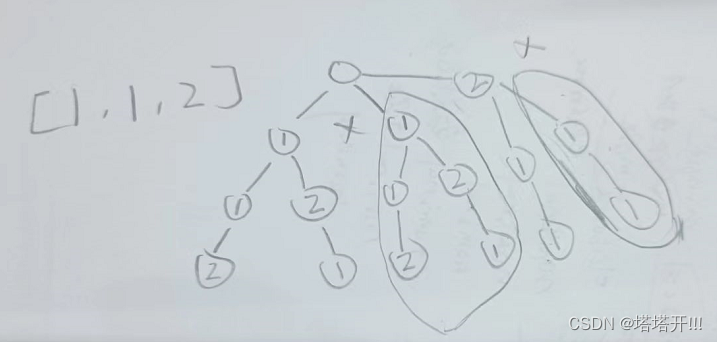
本题与上一题的区别：数组存在重复元素，要对结果集进行去重：

• 排序
• 重复的元素每次只以第一个元素为准即可，以第一个重复的元素去递归访问即可，后面的重复元素遇到直接跳过（剪枝）

Code

class Solution {
    int N = 25;
    int n;
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    boolean[] st = new boolean[N];
    public List<List<Integer>> permuteUnique(int[] nums) {
        n = nums.length;
        Arrays.sort(nums);
        dfs(nums, 0);
        return res;
    }
    public void dfs(int[] nums, int u){
        if(u == n){
            res.add(new ArrayList(path));
            return ;
        }
        // 枚举每一种可能
        for(int i = 0; i < n; i ++){
            
            // 剪枝（跳过重复的枝条）
            if(i > 0 && nums[i] == nums[i - 1] && st[i - 1] == true) continue;

            if(!st[i]){
                st[i] = true;
                path.add(nums[i]);
                dfs(nums, u + 1);
                st[i] = false;
                path.remove(path.size() - 1);
            }
        }
    }
}

五、棋盘问题

13. N 皇后

题目链接：51. N 皇后 - 力扣（LeetCode）

思路：N皇后模板题

Code

class Solution {
    int N = 25;
    boolean[] col = new boolean[N];
    boolean[] dg = new boolean[N];
    boolean[] udg = new boolean[N];
    char[][] g = new char[N][N];
    int n;
    List<List<String>> res = new ArrayList<>();
    public List<List<String>> solveNQueens(int _n) {
       n = _n;
       for(int i = 0; i < n; i ++){// 棋盘初始化
           for(int j = 0; j < n; j ++){
               g[i][j] = '.';
           }
       } 
       dfs(0);// 从第0行开始
       return res;
    }
    public void dfs(int u){
        if(u == n){
            List<String> tmp = new ArrayList<>();
            String str = "";
            for(int i = 0; i < n; i ++){
                for(int j = 0; j < n; j ++){
                    str += g[i][j];
                }
                tmp.add(str);// 加入棋盘的每一行
                str = "";// 为下一次做好准备
            }
            res.add(new ArrayList(tmp));
            return ;
        }
        // 枚举所有列
        for(int i = 0; i < n; i ++){
            if(!col[i] && !dg[u + i] && !udg[u - i + n]){
                col[i] = dg[u + i] = udg[u - i + n] = true;
                g[u][i] = 'Q';
                dfs(u + 1);
                col[i] = dg[u + i] = udg[u - i + n] = false;
                g[u][i] = '.';
            }
        }
    }
}

14. N皇后 II

题目链接：52. N皇后 II - 力扣（LeetCode）

思路：N皇后模板题

Code

class Solution {
    int N = 25;
    boolean[] col = new boolean[N];
    boolean[] dg = new boolean[N];
    boolean[] udg = new boolean[N];
    char[][] g = new char[N][N];
    int n;
    int res = 0;

    public int totalNQueens(int _n) {
       n = _n;
       for(int i = 0; i < n; i ++){
           for(int j = 0; j < n; j ++){
               g[i][j] = '.';
           }
       } 
       dfs(0);// 从第0行开始
       return res;
    }
    public void dfs(int u){
        if(u == n){
            res ++;
            return ;
        }
        // 枚举所有列
        for(int i = 0; i < n; i ++){
            if(!col[i] && !dg[u + i] && !udg[u - i + n]){
                col[i] = dg[u + i] = udg[u - i + n] = true;
                g[u][i] = 'Q';
                dfs(u + 1);
                col[i] = dg[u + i] = udg[u - i + n] = false;
                g[u][i] = '.';
            }
        }
    }
}

15. 解数独

题目链接：37. 解数独 - 力扣（LeetCode）

Code

思路：和N皇后的思路很像，只是扩展到了二维递归。

从前往后枚举每一个空格该填哪一个数。

状态：row[9][9]，col[9][9]，cell[3][3][9]

每一行、每一列、每一个九宫格里边只能填不一样的数字，判断是否可以选：

row[9][9]：row[i][x],当前第i行选的是哪一个数字（选的数字x）

col[9][9]：col[i][x],当前第i列选的是哪一个数字（选的数字x）

cell[3][3][9]：cell[i][j][x]，九宫格中(i, j)位置填的数为x

Code

class Solution {
    boolean[][] row = new boolean[10][10];
    boolean[][] col = new boolean[10][10];
    boolean[][][] cell = new boolean[3][3][10];

    public void solveSudoku(char[][] g) {
        // 初始化
        for(int i = 0; i < 9; i ++){
            for(int j = 0; j < 9; j ++){
                if(g[i][j] != '.'){// 不是空格（题目填好的数字）
                    int t = g[i][j] - '0';
                    row[i][t] = col[j][t] = cell[i / 3][j / 3][t] = true;// 标记已用过
                }
            }
        }
        dfs(g, 0, 0);
    }
    public boolean dfs(char[][] g, int x, int y){
        // 判断边界
        if(y == 9){
            x ++;
            y = 0;
            if(x == 9) return true;
        }
        if(g[x][y] != '.') return dfs(g, x, y + 1);// 若当前数已经填过了，就跳过

        // 枚举所有可能情况
        for(int val = 1; val <= 9; val ++){
            if(!row[x][val] && !col[y][val] && !cell[x / 3][y / 3][val]){
                g[x][y] = (char)('0' + val);// 转为字符
                row[x][val] = col[y][val] = cell[x / 3][y / 3][val] = true;
                if(dfs(g, x, y + 1)) return true;// 填下一个数
                g[x][y] = '.';// 恢复现场
                row[x][val] = col[y][val] = cell[x / 3][y / 3][val] = false;
            }
        }
        return false;
    } 
}

六、其他

16. 递增子序列

题目链接：491. 递增子序列 - 力扣（LeetCode）

思路：递归回溯枚举所有组合：

• 注意去重（由于不能排序，那么我们用之前的去重条件剪枝，只能达到部分去重的目的，结果集仍然可能存在重复集合，如1 3 4 1 1），当枚举到这两个1时，结果集[1, 1]还是会重复的，为了达到去重的目的，我们可以用一个Set集合来记录结果集。
• 要保证选择的序列是递增的

Code

class Solution {
    HashSet<List<Integer>> res = new HashSet<>();
    List<Integer> path = new ArrayList<>();
    int n;
    public List<List<Integer>> findSubsequences(int[] nums) {
        n = nums.length;
        dfs(nums, 0);
        return new ArrayList<List<Integer>>(res);
    }
    public void dfs(int[] nums, int satrt){
        if(path.size() >= 2){
            res.add(new ArrayList(path));
            // 这里不能return ， 答案有多种不能直接结束递归了
        }

        // 枚举所有可能
        for(int i = satrt; i < n; i ++){
            // 去重剪枝
            if(i > satrt && nums[i] == nums[i - 1]) continue;// 但是并不能达到完全重重的目的（因为我们没有排序（不能排序），结果集仍然会有重复的）
            // 保证序列是递增的
            if(path.size() > 0 && nums[i] < path.get(path.size() - 1)) continue;

            path.add(nums[i]);
            dfs(nums, i + 1);
            path.remove(path.size() - 1);
        }
    }
}

17. 重新安排行程

题目链接：332. 重新安排行程 - 力扣（LeetCode）

思路：这题很像是一个图，找到一个路线形成图，我们依然可以使用递归回溯，枚举所有方案，找到一条符合答案的路线，由于可能存在多组解，但题目要求我们在多组解的情况下取字典序最小的解，每一次递归枚举时如何获得字典序最小得城市呢？

• 由于一个form可能对应多个to，我们用map存储信息时，value（to）用一个优先队列来维护（默认小根堆）即得到字典序最小得这段路线信息了！
• from找到des就一直递归，直到最终找完完整路线（答案），递归结束回溯得时候加入res集合即可，翻转后即为答案所求路线！

Code

class Solution {
    Map<String, PriorityQueue<String>> mp = new HashMap<>();
    List<String> res = new ArrayList<>();
    public List<String> findItinerary(List<List<String>> tickets) {
        // 存信息
        for(List<String> tic : tickets){
            String src = tic.get(0), des = tic.get(1);
            if(!mp.containsKey(src)) mp.put(src, new PriorityQueue<String>());
            mp.get(src).offer(des);// 目的地加入优先队列
        }
        dfs("JFK");
        Collections.reverse(res);
        return res;
    }
    public void dfs(String s){
        
        // 枚举路线
        while(mp.containsKey(s) && mp.get(s).size() >= 1){
            String des = mp.get(s).poll();// 拿到字典序最小得des
            dfs(des);
        }
        res.add(s);// 找到完整路线（递归结束回溯的时候甜的，最后要将路线翻转才得到答案路线）
    }
}