选择排序（这里实现升序）

实现思想：遍历数组找出最大或最小的数，交换到数组末尾（最大）或者数组起始位置（最小），直到数组完成有序。

动图演示（演示的是找最小的）

?void Swap(int* a, int* b)//传址，才能完成交换，否则形参不会改变实参。
{
?? ?int tmp = *a;
?? ?*a = *b;
?? ?*b = tmp;//交换函数
}
void SelectSort(int* a, int n)
{
?? ?int begin = 0;
?? ?int i = 0;
?? ?while (begin < n)
?? ?{
?? ??? ?int min = begin;//记录最小值下标，min从begin位置开始找数组未完成排序的最小值。
?? ??? ?for (i = begin; i < n; i++)
?? ??? ?{
?? ??? ??? ?if (a[min] > a[i])
?? ??? ??? ?{
?? ??? ??? ??? ?min = i;//更新min位置
?? ??? ??? ?}
?? ??? ?}
?? ??? ?Swap(&a[begin], &a[min]);
?? ??? ?begin++;//第一轮排序后，数组最小值已经完成排序，begin++，排序区间往后移。
?? ?}
}

这里可以优化一点，循环找最小位置的下标同时把最大位置的下标也找出来，最小的往前交换，最大的往后交换，（begin++,end--）区间改变，这样效率快一倍，但是有特殊情况要处理。

void SelectSort(int* a, int n)
{
?? ?int begin = 0;//需要排序数组开始位置
?? ?int end = n - 1;//需要排序数组最后位置
?? ?int i = 0;
?? ?while (begin < end)//begin=end,一个元素不需要处理
?? ?{
?? ??? ?int min = begin;//记录最小值下标
?? ??? ?int max = begin;//记录最大值下标
?? ??? ?for (i = begin; i <= end; i++)
?? ??? ?{
?? ??? ??? ?if (a[min] > a[i])
?? ??? ??? ?{
?? ??? ??? ??? ?min = i;//更新min位置
?? ??? ??? ?}
?? ??? ??? ?if (a[max] < a[i])
?? ??? ??? ?{
?? ??? ??? ??? ?max = i;//更新mxa位置
?? ??? ??? ?}
?? ??? ?}
?? ??? ?Swap(&a[begin], &a[min]);//这里先交换最小值位置与begin位置元素
?? ??? ?if (max == begin)//判断一下最大值是否在begin位置上
?? ??? ?{
?? ??? ??? ?max = min;//如果是，交换后，最大值就在min下标位置
?? ??? ?}
?? ??? ?Swap(&a[end], &a[max]);
?? ??? ?begin++;
?? ??? ?end--;
?? ?}
}
?

时间复杂度最好最坏都是O(N^2)? 空间复杂度O(1)。?

堆排序?

实现思想，如果排升序，得先建一个大堆，在通过向下调节完成排序。

建堆

向下调节算法
若想将其调整为小堆，那么根结点的左右子树必须都为小堆。
若想将其调整为大堆，那么根结点的左右子树必须都为大堆。

所以我们得最后一个非叶子节点的左右孩子节点开始调堆。

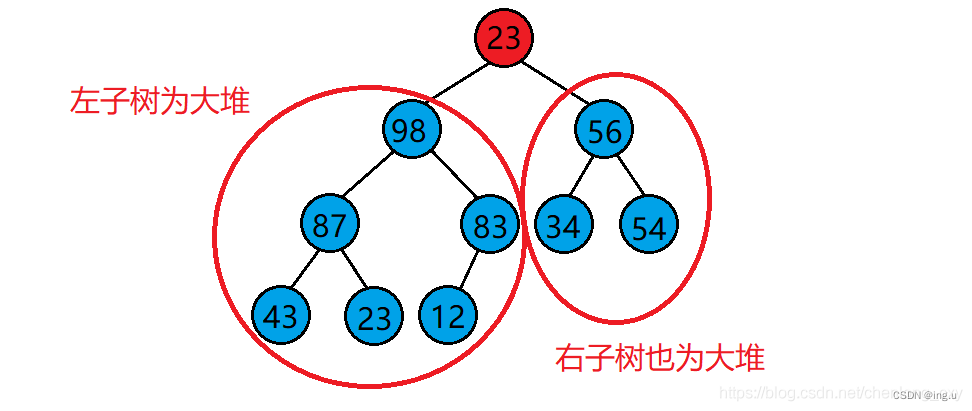
思想实现（建大堆）

向下调整算法思想

1.从根结点处开始，找出左右孩子大的那个节点
2.大的节点与父亲节点比较
? ? 若大的孩子比父亲节点还要大，则与父亲节点位置交换，并让这个节点为新的父亲节点，继续向下调整直到叶子节点为止，
?若大的孩子比父亲小，则不需处理了，调整完成，整个树已经是大堆了。

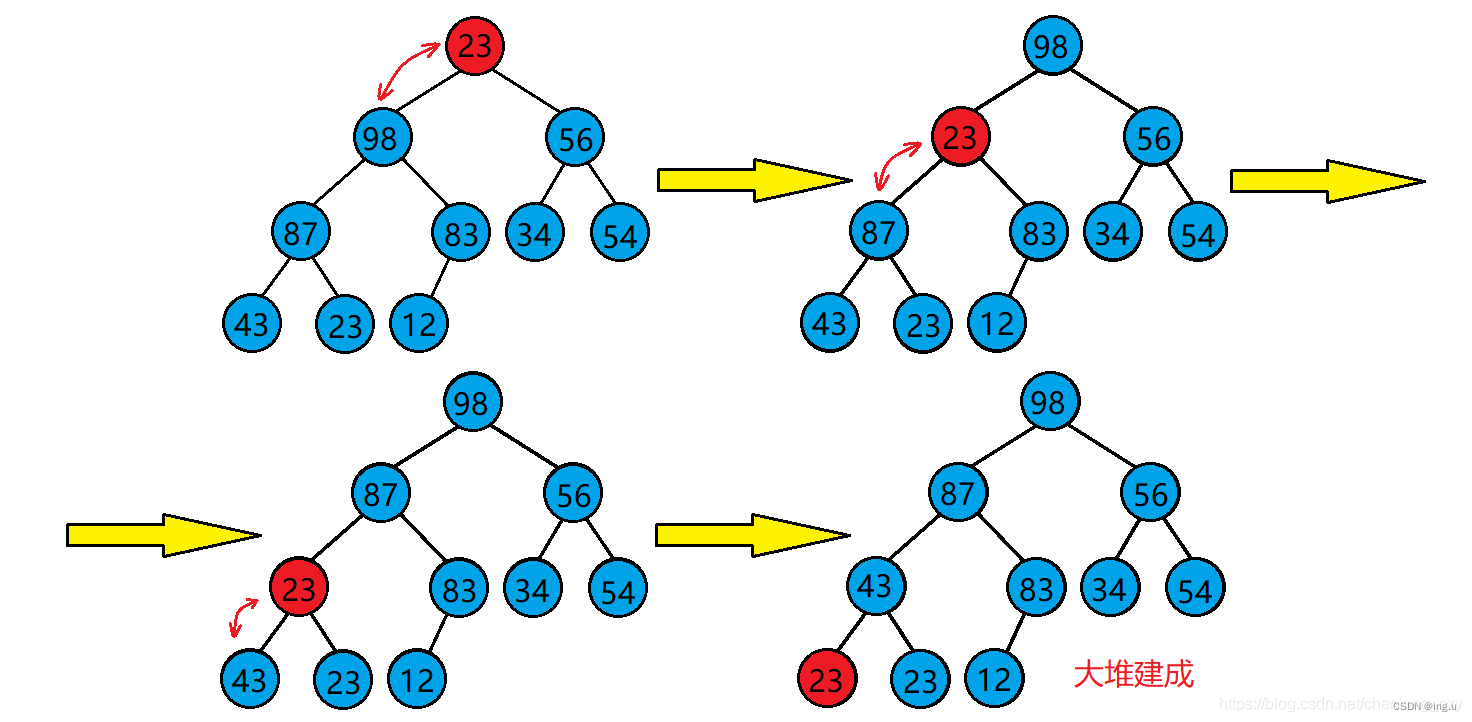
?void AdjustHeapDown(int* a, int size, int parent)
{
?? ?int child = parent * 2 + 1;? //左孩子下标
?? ?while (child < size)//child>=size时，已经不在堆中了
?? ?{
?? ??? ?if (child + 1 < size && a[child + 1] > a[child])//child+1<size表示右孩子存在
?? ??? ?{
?? ??? ??? ?child++;//表示右孩子的值大于左孩子的值，与父亲节点比较的值是右孩子
?? ??? ?}
?? ??? ?if (a[child] > a[parent])
?? ??? ?{
?? ??? ??? ?Swap(&a[child], &a[parent]);//交换父亲孩子节点位置
?? ??? ??? ?parent = child;//父亲迭代到该孩子节点
?? ??? ??? ?child = parent * 2 + 1;//下一个需要比较的孩子节点位置
?? ??? ?}
?? ??? ?else
?? ??? ?{
?? ??? ??? ?break;//已经满足堆的条件，跳出本次循环
?? ??? ?}
?? ?}
}

有了向下调整思想，怎样将一个任意的二叉树调成堆呢?？

因为要左右节点都满足堆的性质，才能向下调整，那我们就可以从第一个非叶子节点下标开始调节，直到调到根结束。

//n-1是最后一个节点位置，公式法求该位置的父亲节点位置，parent=(child-1)/2。
??for (int i = (n - 1 - 1) / 2; i >= 0; i--)// i=0时，左右都满足大堆，最后一次从根节点调
??{
?? ???AdjustHeapDown(a, n, i);//n是二叉树的节点个数
??}

建堆的时间复杂度（每层节点数*向下调节次数）

最后一层叶子节点不需要向下调节，所以只需要调到倒数第二层节点

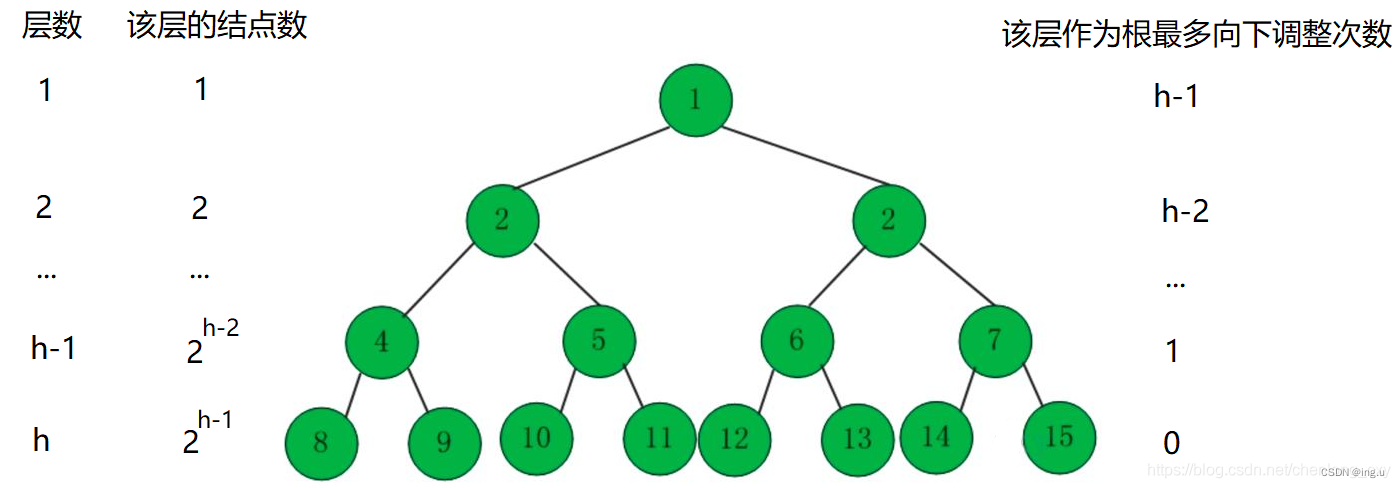
堆排序

思想实现：

1.堆顶元素与最后一个元素交换

2.从根位置执行向下调整算法，但是此时最后一个位置不属于向下调整算法区间（此时该值已经排好），通过end--,调整区间往前移，重复执行1,2，直到end=0时（区间只有一个节点），完成排序。

void HeapSort(int* a, int n)
{

? ? //建堆
?? ?for (int i = (n - 1 - 1) / 2; i >= 0; i--)
?? ?{
?? ??? ?AdjustHeapDown(a, n, i);
?? ?}

? ?
?? ?int index = n - 1;//最后一个元素位置
?? ?while (index > 0)
?? ?{
?? ??? ?Swap(&a[0], &a[index]);
?? ??? ?AdjustHeapDown(a, index, 0);
?? ??? ?index--;
?? ?}
}