文章目录
一、排序小老弟——选择排序
1.排序思想

通过上图可知选择排序的基本逻辑:依次选出最小,次小,次次小…
2.代码实现及复杂度计算
void SelectSort(int* a, int n)
{
int i,j,min,tmp;
for(i=0;i<n-1;i++)
{
min=i;
for(j=i+1;j<n;j++)
{
if(a[min]>a[j])
min=j;
}
tmp=a[i];
a[i]=a[min];
a[min]=tmp;
}
}
时间复杂度:N^2,且不受数据有序程度影响。
空间复杂度:1。
二、排序二老弟——冒泡排序

1.排序思想
通过上图可知冒泡排序的基本逻辑:两两比较,前大则交换,每次都可将最大数放至最后。
2.代码实现及复杂度计算
void BubbleSort(int* a, int n)
{
int i,j,tmp;
for(i=n;i>0;i--)
{
int flag=0;//优化
for(j=0;j<i;j++)
{
if(a[j]<a[j-1])
{
tmp=a[j];
a[j]=a[j-1];
a[j-1]=tmp;
flag=1;
}
}
if(flag==0)
break;
}
}
时间复杂度:N^2,经优化,当数据有序时,则时间复杂度为N。
空间复杂度:1。
三、小老弟最强——插入排序

1.排序思想
通过上图可知插入排序的基本逻辑:新数据与有序序列从后向前依次比较,放置在比它小的数字前。
2.代码实现及复杂度计算
void InsertSort(int* a, int n)
{
for (int i = 0; i < n - 1; ++i)
{
// [0,end] 插入 end+1 [0, end+1]有序
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + 1] = a[end];
--end;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
时间复杂度:N^2,当数据有序时,则时间复杂度为N。
空间复杂度:1。
四、选择排序超进化——堆排序
1.排序思想

我们知道选择排序是不断选最值,而堆的堆顶就是最值,由此我们衍生出了堆排序。
通过上图可知堆排序的基本逻辑:建大根堆后,将堆顶元素与尾元素互换,然后向下调整,不断重复。
2.代码实现及复杂度计算
void HeapSort(int* a, int n)
{
//建堆
for (int i = n/2-1;i>= 0;--i)
{
AdjustDown(a, n, i+1);
}
//排序
for(int i=n-1;i>0;i--)
{ int tmp=a[i];
a[i]=a[0];
a[0]=tmp;
AdjustDown(a, --n, 1);
}
}
void AdjustDown(int* a, int n,int i)
{
int tmp,max;
if(i*2+1<=n)
max=a[i*2-1]>a[i*2]?i*2:i*2+1;
else if(i*2<=n)
max=i*2;
else
return ;
while(1)
{
if(a[i-1]<a[max-1])
{tmp=a[max-1];
a[max-1]=a[i-1];
a[i-1]=tmp;
i=max;
if(i*2+1<=n)
max=a[i*2-1]>a[i*2]?i*2:i*2+1;
else if(i*2<=n)
max=i*2;
else
return ;
}
else
return ;
}
}
时间复杂度:N*logN,且不受数据有序程度影响。
空间复杂的:1。
3.建堆方式的选择
其实建堆方式有向上调整建堆与向下调整建堆。
对于一个有N个节点,高为h的树来说
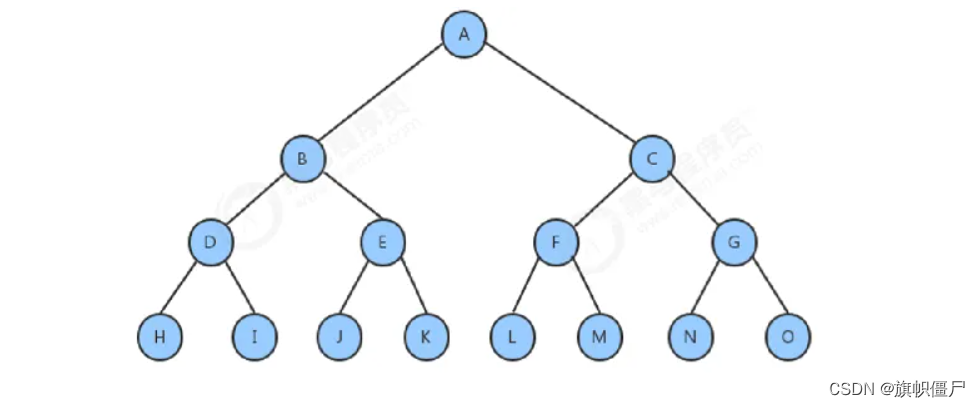
1.向上调整建堆
从第一个节点开始,从前往后,不断向上调整
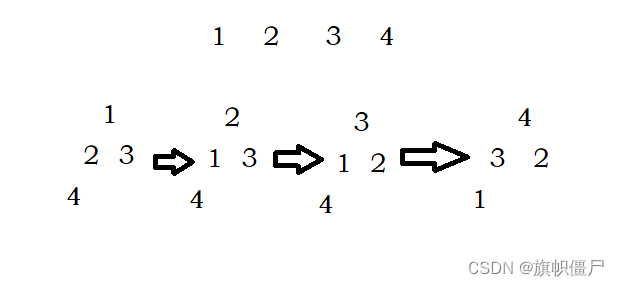
那么最坏情况为:
第2层,有2^1个节点向上移动1层
第3层,有2^2个节点向上移动2层
…
第h层,有2^h-1个节点向上移动h-1层
通过错位相减法,其和大致=N*logN
2.向下调整建堆
从最后一个非叶子节点开始,从后向前,不断向下调整
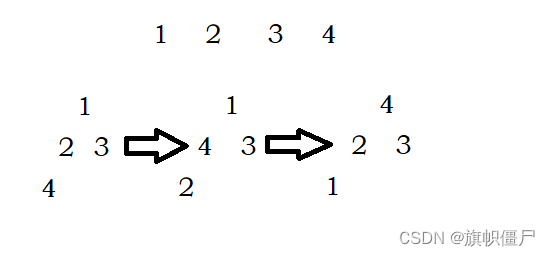
那么最坏情况为:
第h-1层,有2^h-2个节点向下移动1层
第h-2层,有2^h-3个节点向下移动2层
…
第1层,有2^0个节点向下移动h-1层
通过错位相减法,其和=N-log(N+1)
五、插入排序超进化——希尔排序
1.排序思想

我们使用插入排序时发现,如果数据越接近于有序,插入排序时间复杂度越小。大佬发现若我们先分组进行插入排序后,再进行插入排序,其效率更高,由此衍生出了希尔排序。
通过上图可知希尔排序的基本逻辑:先以gap为间隔进行分组插入排序,之后再进行插入排序。
2.代码实现及复杂度计算
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
//gap = gap / 2;
gap = gap / 3 + 1;
// [0,end] 插入 end+gap [0, end+gap]有序 -- 间隔为gap的数据
for (int i = 0; i < n - gap; ++i)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
时间复杂度:N^1.3,当数据有序时,则时间复杂度为N。
空间复杂度:1
六、唯一外排——归并排序

1.排序思想
其思想与树的子问题划分类似:
若数据前一半为有序,后一半有序,那我们将它们相互比较,插入至新数组再拷贝回原数组即可。
而我们要得到前一半有序的数据,则再将它划分即可
2.代码实现及复杂度计算
递归法:
void f(int *a,int left,int right,int *tmp)
{
if(left>=right)
return ;
f(a,left,(left+right)/2,tmp);
f(a,(left+right)/2+1,right,tmp);
int mid=(left+right)/2;
int i=left;
while(left<=(left+right)/2&&mid<=right)
{
if(a[left]>a[mid+1])
{
tmp[i++]=a[mid+1];
mid++;
}
else
{
tmp[i++]=a[left];
left++;
}
}
while(left<=(left+right)/2)
{
tmp[i++]=a[left];
left++;
}
while(mid<=right)
{
tmp[i++]=a[mid+1];
mid++;
}
memcpy(a+left,tmp+left,(right-left+1)*sizeof(int));
}
void MergeSort(int *a,int n)
{
int *tmp=(int*)malloc(sizeof(int)*n);
f(a,0,n-1,tmp);
free(tmp);
}
非递归:
void MergeSort(int *a,int n)
{
int *tmp=(int*)malloc(sizeof(int)*n);
int gap=1;
while(gap<n)
{
int begin1=0;
int i=begin1;
int end1=begin1+gap-1;
int begin2=end1+1;
int end2=begin2+gap-1;
while(1)
{
int begin=begin1;
while(begin1<=end1&&begin2<=end2)
{
if(a[begin1]>a[begin2])
{
tmp[i++]=a[begin2];
begin2++;
}
else
{
tmp[i++]=a[begin1];
begin1++;
}
}
while(begin1<=end1)
{
tmp[i++]=a[begin1];
begin1++;
}
while(begin2<=end2)
{
tmp[i++]=a[begin2];
begin2++;
}
memcpy(a+begin,tmp+begin,(end2-begin+1)*sizeof(int));
begin1=end2+1;
end1=begin1+gap-1;
begin2=end1+1;
end2=begin2+gap-1;
if(begin2>n-1)
break;
else if(end2>=n)
end2=n;
}
gap=gap*2;
}
}
时间复杂度:N*logN,且不受数据有序程度影响。
空间复杂度:N
七、排序老大哥——快排(霍尔排序)
1.排序思想
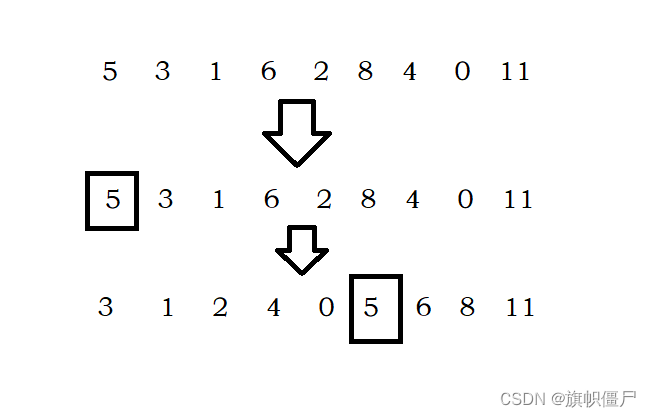
快排思想:
在一组数据中,先选定任意一个数作为基数,然后将比这个数字小的数放在它的左边,比它大的放在它的右边。经过一次,则基数处于正确位置,且它将数据分割成了2个空间,再以相同方法处理这两个空间即可。
有3种常用方法可以实现一趟快排。
1.霍尔法

右指针先移动,当遇到比基数小的数字则停止
左指针再移动,当遇到比基数大的数字停止,交换左右指针所指数字,不断循环,直至左右指针相遇,此时将该数字与基数交换。
2.挖坑法

将基数拿出,基数位置当作第一个坑位
右指针先移动,当遇到比基数小的数字,将该数字填入坑位,该数位置成为新坑位
右指针先移动,当遇到比基数大的数字,将该数字填入坑位,该数位置成为新坑位,不断循环,直至两指针相遇,将基数填入坑位
3.前后指针法

2.代码实现及复杂度计算
void QuickSort(int* a, int begin, int end)//霍尔法
{
if(begin>=end)
return;
int key=begin;
int left=begin;
int right=end;
while(left<right)
{
while(left<right)
{
if(a[right]>=a[key])
right--;
else
break;
}
while(left<right)
{
if(a[left]<=a[key])
left++;
else
break;
}
swap(a[left],a[right]);
}
swap(a[key],a[right]);
QuickSort(a,begin,left-1);
QuickSort(a,left+1,end);
}
void QuickSort(int* a, int begin, int end)//挖坑法
{
if(begin>=end)
return;
int keynum=a[hole];
int hole=begin;
int left=begin;
int right=end;
while(left<right)
{
while(left<right)
{
if(a[right]>=a[key])
right--;
else
{
a[hole]=a[right];
hole=right;
break;
}
}
while(left<right)
{
if(a[left]<=a[key])
left++;
else
{
a[hole]=a[left];
hole=left;
break;
}
}
}
a[hole]=keynum;
QuickSort(a,begin,left-1);
QuickSort(a,left+1,end);
}
void QuickSort(int* a, int begin, int end);//前后指针法
{
if(begin>=end)
return;
int pre,key,cur;
pre=key=cur=begin;
cur++;
while(cur<=end)
{
if(a[cur]<a[key])
{ pre++;
swap(a[pre],a[cur]);
}
cur++;
}
swap(a[pre],a[key]);
QuickSort(a,begin,key-1);
QuickSort(a,key+1,end);
}
void QuickSort(int* a, int begin, int end)//非递归法
{
begin,end进栈;
while(栈不为空)
{
出栈;
int key=part(a,出栈元素1,出栈元素2);
if(出栈元素1<key)
出栈元素1与key进栈;
if(出栈元素2>key)
出栈元素2与key进栈;
}
}
void part(int* a, int begin, int end)这里用的是前后指针,用哪个都行
{
int pre,key,cur;
pre=key=cur=begin;
cur++;
while(cur<=end)
{
if(a[cur]<a[key])
{ pre++;
swap(a[pre],a[cur]);
}
cur++;
}
swap(a[pre],a[key]);
return key;
}
时间复杂度:N*logN,且不受数据有序影响。
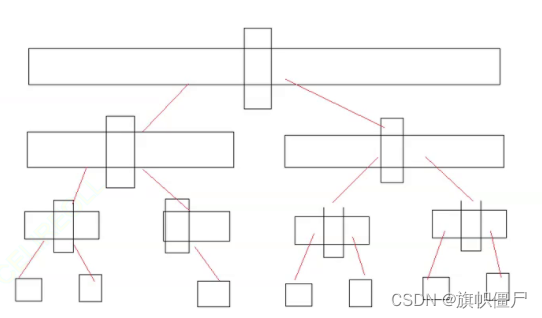
其递归深度大约为logN,每层大概排N次
若数据有序,或逆序,其时间复杂度为N^2,可用三数取中法(在初位置,末位置,与中间位置选中间数值的数作为基数)或随机数法(随机选一个数作为基数)优化。
三数取中代码如下:
void GetMid(int *a,int begin,int end)
{
int x=(begin+end)/2;
if(a[x]>a[begin])
{
if(a[x]>a[end])
return a[begin]>a[end]?begin:end;
else
return x;
}
else
{
if(a[x]>a[end])
return x;
else
return a[begin]>a[end]?end:begin;
}
}
空间复杂度:logN
递归:其大概建立logN层栈帧
非递归:若每次key都在中间位置,其在最后一次要入栈logN个数
八、特况最优解——计数排序
1.排序思想
对于一组数据,计数排序会建立一个大小为数据极差的数组。
将数据中每一个数字的个数存起来,然后依次输入至原数组。
其无法排序浮点型。
2.代码实现及复杂度计算
void CountSort(int *a,int n)
{
int i=1,j=0;
int min=a[0];
int max=a[0];
while(i<n)
{
if(a[i]<min)
min=a[i];
if(a[i]>max)
max=a[i];
i++;
}
int num[max-min+1]={0};
for(i=0;i<n;i++)
{
num[a[i]-min]++;
}
i=0;
while(i<n)
{
if(num[j]==0)
{
j++;
}
else
{
a[i++]=j+min;
num[j]--;
}
}
}
设其数据范围为M
时间复杂度:N*M
空间复杂度:M
九、排序汇总
| 排序方法 | 时间 | 是否受有序影响 | 空间 | 稳定性 | 使用场合 |
|---|---|---|---|---|---|
| 选择 | N^2 | 否 | 1 | 不稳定 | 小老弟 |
| 冒泡 | N^2 | 否 | 1 | 稳定 | 二老弟 |
| 插入 | N^2 | 有序时为N | 1 | 稳定 | 老弟最猛的 |
| 堆排 | N*logN | 否 | 1 | 不稳定 | topK问题 |
| 希尔 | N^1.3 | 有序时为N | 1 | 不稳定 | 数据规模中等 |
| 归并 | N*logN | 否 | N | 稳定 | 涉及文件(外排) |
| 快排 | N*logN | 否,优化前有序时为N^2 | logN | 不稳定 | 正常情况下最优选 |
| 计数 | N+M | 否 | M | 稳定 | 数据集中(整形) |
总结
排序作为一个重难点,需要各位好好学。
希望大家都能手撕快排。