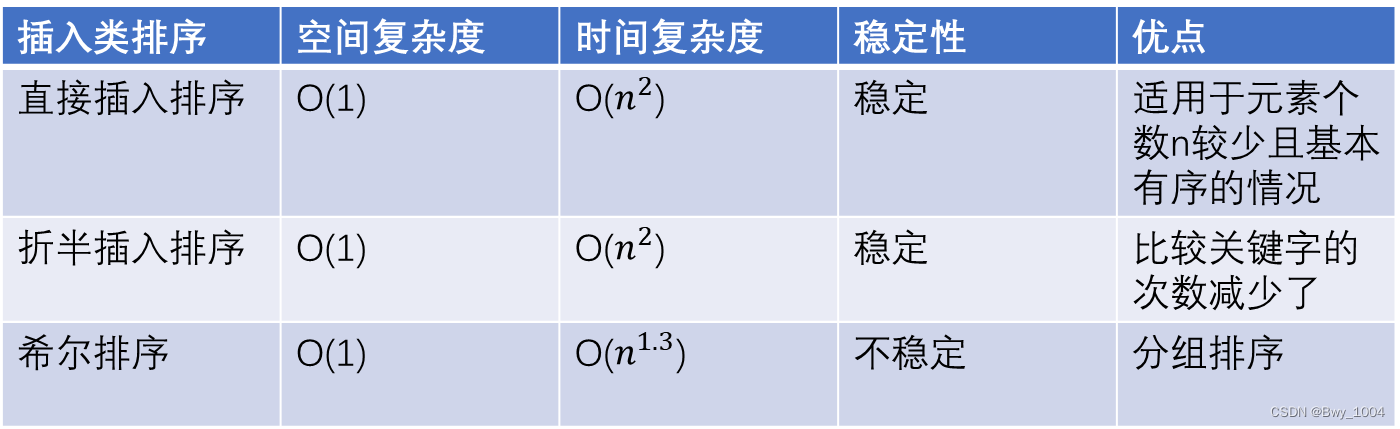
一、排序算法的评价指标
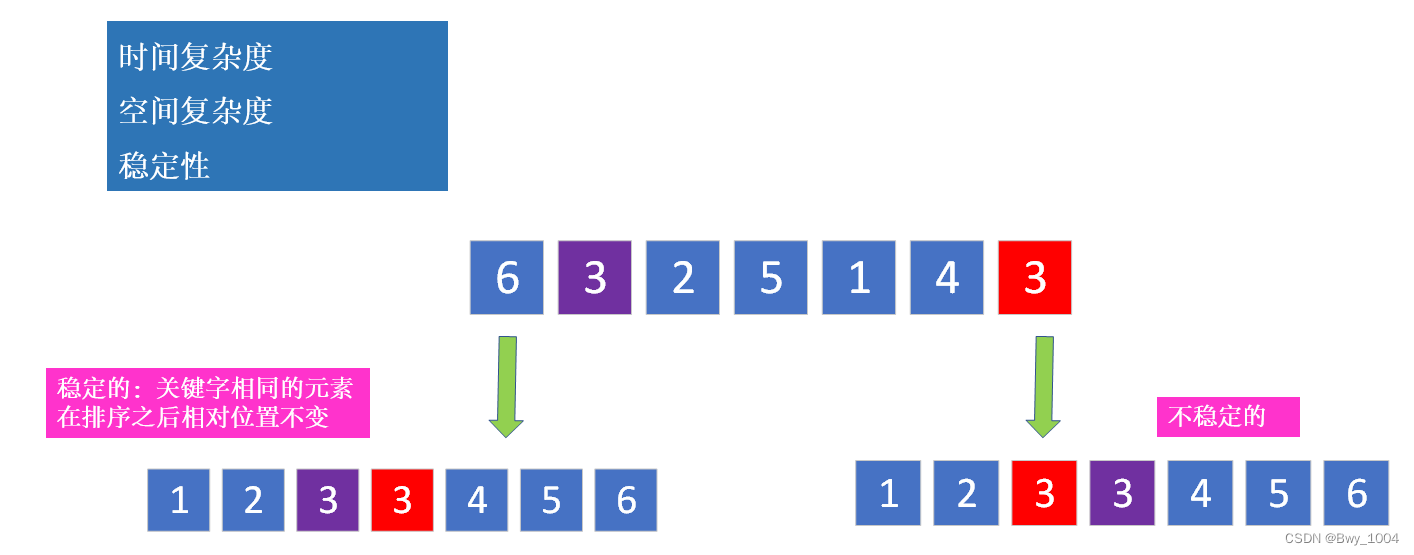
二、排序算法(内部排序)
2.1 插入类排序
2.1.1 直接插入排序
算法思想:每次将一个待排序的记录按其关键字大小插入到前面已排好序的子序列当中,直到全部记录插入完成。
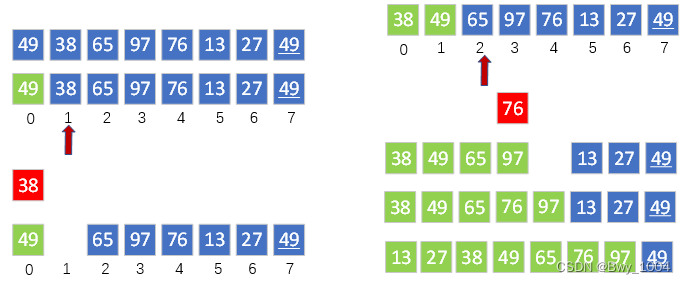
算法实现:

代码实现:
//直接插入排序
void InsSort(int A[],int n){
//A数组存放待排序元素 n表示元素个数
int i,j,temp;
for(i=1;i<n;i++){ //将各元素插入已排好序的序列中
if(A[i-1]>A[i]){ //若A[i]的关键字小于前一个值
temp=A[i]; //用temp暂存A[i]
for(j=i-1;j>=0&&A[j]>temp;j--){ //与已排好序的元素进行比较
A[j+1]=A[j]; //大于temp的元素都向后挪
}
A[j+1]=temp;
}
}
}
/*
* 时间复杂度:
* 最坏情况:O(n^2) 最好情况(有序时):O(n)
* 空间复杂度:O(1)
* 稳定性:稳定
*/
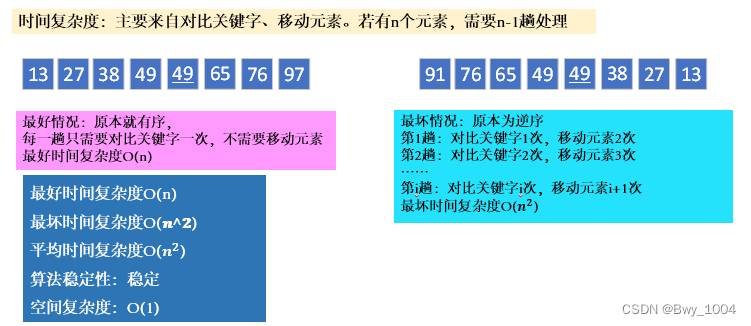
时间复杂度分析:
2.1.2 折半插入排序
算法思想:先用折半查找找到应该插入的位置,再移动元素
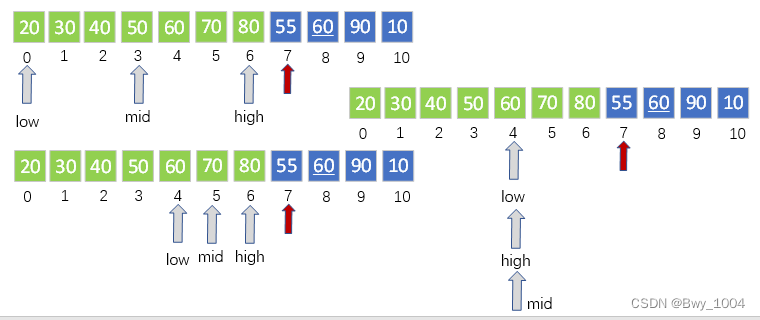
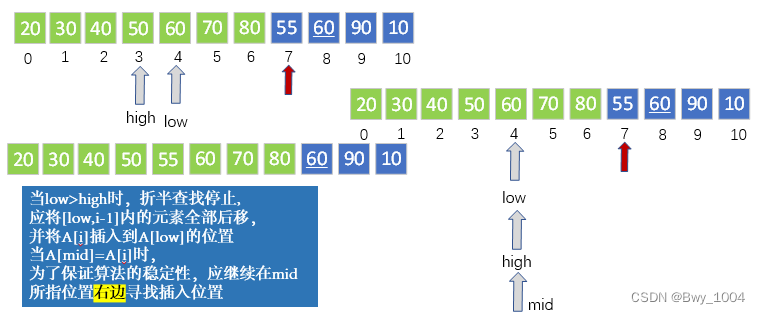
算法实现:

代码实现:
//折半插入排序
void BinSort(int A[],int n){
//进行折半插入排序
int low,high,mid,temp;
int i,j;
for(i=1;i<n;i++){
low=0;
high=i-1;temp=A[i];
while(low<=high){
mid=(low+high)/2;
if(A[i]>=A[mid]){
low=mid+1;
}else{
high=mid-1;
}
}
for(j=i-1;j>=low;j--){
A[j+1]=A[j];
}
A[j+1]=temp;
}
}
/*
* 时间复杂度:
* 最坏情况:O(n^2) 最好情况(有序时):O(n)
* 空间复杂度:O(1)
* 稳定性:稳定
*/
时间复杂度分析:

2.1.3 希尔排序
算法思想:先追求表中元素部分有序,再逐渐逼近全局有序
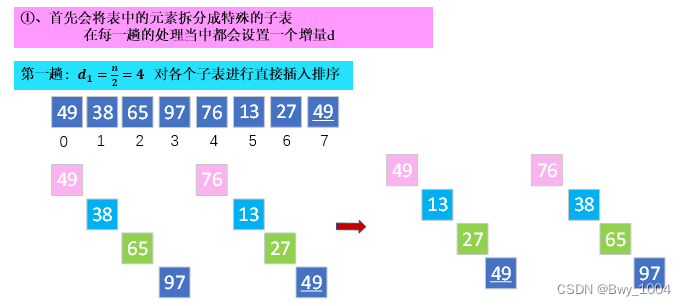
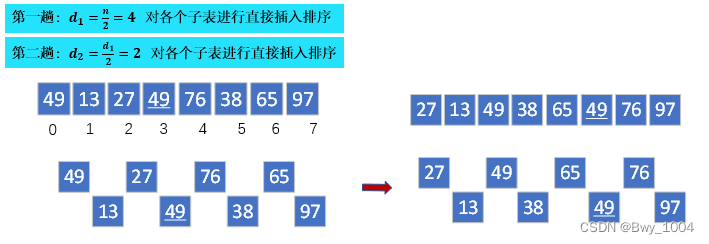
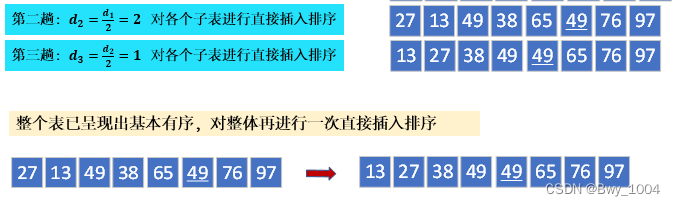
算法实现:

代码实现:
//希尔排序
void ShellInsert(int A[],int n){
int i,j,d,temp;
for(d=n/2;d>=1;d=d/2){
for(i=d;i<n;i++){
if(A[i-d]>A[i]){
temp=A[i-d];
for(j=i-d;j>=0&&A[j]>temp;j=j-d){ //直接插入排序
A[j+d]=A[j]; //大于temp的元素都向后挪
}
A[j+d]=temp;
}
}
}
}
/*
* 时间复杂度:
* 最坏情况:O(n^1.3) 最好情况(有序时):O(n)
* 空间复杂度:O(1)
* 稳定性:不稳定
*/
时间复杂度分析:

稳定性分析:
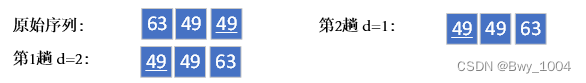
不稳定
总结