一【题目类别】

深度优先搜索

二【题目难度】

中等

三【题目编号】

236.二叉树的最近公共祖先

四【题目描述】

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

五【题目示例】

示例 1：
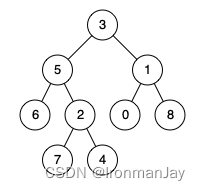
- 输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
- 输出：3
- 解释：节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2：
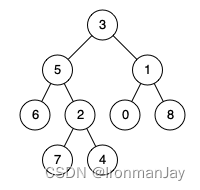
- 输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
- 输出：5
- 解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3：
- 输入：root = [1,2], p = 1, q = 2
- 输出：1

六【解题思路】

这个题本来想利用数组根据下标去找公共祖先，但是这显然是不允许的，以为题目给的二叉树并不是完全二叉树
那么我们就需要换一个思路
我们首先遍历这棵树，判断是否能找到题目给定的节点（p=left,q=right），一共分四种情况
- left和right都不为空：说明p和q异侧，root就是最近的公共祖先，返回root
- left和right都为空：说明二叉树中不存在p和q，返回null
- left不为空right为空：p和q同侧（left侧），最近公共祖先在left，返回left
- right不为空left为空：p和q同侧（right侧），最近公共祖先在right，返回right

七【题目提示】

$树中节点数目在范围 [2, 10^5] 内。$
$10^9 <= Node.val <= 10^9$
$所有 N o d e . v a l 互不相同。$
$p! = q$
$p 和 q 均存在于给定的二叉树中。$

八【时间频度】

时间复杂度： $O (n)$ ，其中 $n$ 是二叉树的节点个数
空间复杂度： $O (n)$ ，其中 $n$ 是二叉树的节点个数

九【代码实现】

Java语言版

package DFS;

public class p236_LowestCommonAncestorOfABinaryTree {

    int val;
    p236_LowestCommonAncestorOfABinaryTree left;
    p236_LowestCommonAncestorOfABinaryTree right;

    public p236_LowestCommonAncestorOfABinaryTree(int val) {
        this.val = val;
    }

    public p236_LowestCommonAncestorOfABinaryTree(int val, p236_LowestCommonAncestorOfABinaryTree left, p236_LowestCommonAncestorOfABinaryTree right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }

    public static void main(String[] args) {
        p236_LowestCommonAncestorOfABinaryTree root = new p236_LowestCommonAncestorOfABinaryTree(3);
        p236_LowestCommonAncestorOfABinaryTree left = new p236_LowestCommonAncestorOfABinaryTree(5);
        p236_LowestCommonAncestorOfABinaryTree right = new p236_LowestCommonAncestorOfABinaryTree(1);
        p236_LowestCommonAncestorOfABinaryTree left1 = new p236_LowestCommonAncestorOfABinaryTree(6);
        p236_LowestCommonAncestorOfABinaryTree left2 = new p236_LowestCommonAncestorOfABinaryTree(2);
        p236_LowestCommonAncestorOfABinaryTree right1 = new p236_LowestCommonAncestorOfABinaryTree(0);
        p236_LowestCommonAncestorOfABinaryTree right2 = new p236_LowestCommonAncestorOfABinaryTree(8);
        p236_LowestCommonAncestorOfABinaryTree left3 = new p236_LowestCommonAncestorOfABinaryTree(7);
        p236_LowestCommonAncestorOfABinaryTree left4 = new p236_LowestCommonAncestorOfABinaryTree(4);
        root.left = left;
        root.right = right;
        left.left = left1;
        left.right = left2;
        left2.left = left3;
        left2.right = left4;
        right.left = right1;
        right.right = right2;
        p236_LowestCommonAncestorOfABinaryTree ree = lowestCommonAncestor(root, left, right);
        System.out.println("ree = " + ree.val);
    }

    public static p236_LowestCommonAncestorOfABinaryTree lowestCommonAncestor(p236_LowestCommonAncestorOfABinaryTree root, p236_LowestCommonAncestorOfABinaryTree p, p236_LowestCommonAncestorOfABinaryTree q) {
        if (root == null) {
            return root;
        }
        if (root == p || root == q) {
            return root;
        }
        p236_LowestCommonAncestorOfABinaryTree left = lowestCommonAncestor(root.left, p, q);
        p236_LowestCommonAncestorOfABinaryTree right = lowestCommonAncestor(root.right, p, q);
        if (left != null && right != null) {
            return root;
        } else if (left != null) {
            return left;
        } else if (right != null) {
            return right;
        }
        return null;
    }

}

C语言版

#include<stdio.h>

struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
};

struct TreeNode* lowestCommonAncestor(struct TreeNode* root, struct TreeNode* p, struct TreeNode* q)
{
	if (root == NULL)
	{
		return root;
	}
	if (root == p || root == q)
	{
		return root;
	}
	struct TreeNode* left = lowestCommonAncestor(root->left, p, q);
	struct TreeNode* right = lowestCommonAncestor(root->right, p, q);
	if (left != NULL && right != NULL)
	{
		return root;
	}
	else if (left != NULL)
	{
		return left;
	}
	else if (right != NULL)
	{
		return right;
	}
	return NULL;
}

/*主函数省略*/