文章目录
- 系列文章目录
- 1.插入排序:(1)直接插入排序
- 2.选择排序:(1)选择排序
- ? ? ? ? ? ? ? ? ? ? ? ?(2)堆排序
- 3.交换排序? ? ?(1)冒泡排序
- ? ? ? ? ? ? ? ? ? ? ? ? ?(2)快速排序
- 4.归并排序
- ? ? ? ? ? ? ? ? ? ? ? ??
这里所有的排序都是指从小到大的排序
稳定性:

指排序后相同元素的 相对位置不变
1.直接插入排序
简而言之就是给每个数据找一个合适的位置给放下
时间复杂度为:O(N2)
空间复杂度为:O(1)
稳定性:稳定

public static void insert(int[]arr,int left,int right)
{
int i=0;
for(i=left+1;i<=right;i++)
{
int j=i-1;
int tmp=arr[i];
while(j>=0)
{
if(arr[i]<arr[j])
{
arr[j+1]=arr[j];
j--;
}
else
{
arr[j+1]=tmp;
}
}
arr[0]=tmp;
}
}2.选择排序
时间复杂度为O(N2)
空间复杂度为O(1)
稳定性:不稳定
(1)选择排序
? ? 一共两种思路
第一种思路是遍历数组:依次找到最小的数据把它放在前面

public static void seletSort(int[] arr) {
int i = 0;
for (i = 0; i < arr.length; i++) {
//int j = i + 1;
int min = i;
for(int j=i+1;j<arr.length;j++) {
if(arr[j]<arr[min])
{
min=j;
}
}
if (min != i) {
int tmp = arr[min];
arr[min] = arr[i];
arr[i] = tmp;
}
}
}第二种思路是
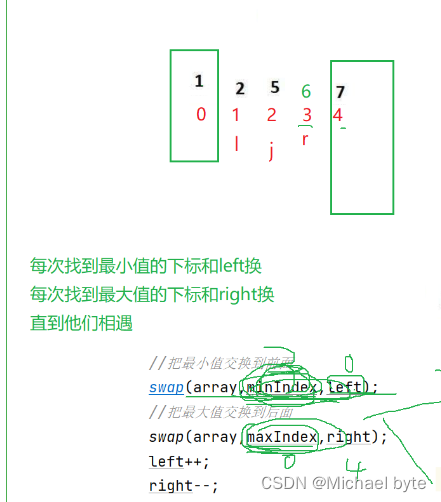
从前往后找最大的,从后往前找最小的,然后把最小的放在最左边,然后把最大的放在最右边,依次类推
public static void seletsort2(int[]arr)
{
int left=0;
int right=arr.length-1;
while(left<right)
{
int min=left;
int max=left;
int i=0;
for(i=left+1;i<=right;i++)
{
if(arr[i]<arr[min])
{
min=i;
}
if(arr[i]>arr[max])
{
max=i;
}
}
swap(arr,min,left);
if(max==left)
{
max=min;
}
swap(arr,max,right);
//swap(arr,min,left);
//arr[left]=arr[min];
//arr[right]=arr[max];
left++;
right--;
}
}这里有一个点我们需要注意:当最前边的元素最大时,

此时left在0位置,right在4的位置,遍历完后此时最小值是1,下标是3,最大值是9在0下标,我们交换后那么最大值就在3?的位置,

此时最大值下标在最小值小标上,我们这时只需将max=min,将最大值下标更新一下就行了。?
3.堆排序
时间复杂度为:O(N*log2N)
空间复杂度:O(1)
稳定性:不稳定
我们可以建立成一个大根堆,然后将头顶元素依次(每个头顶元素都是当前大根堆里最大的元素)和最后一个元素交换
public static void creat() //如果是从小到大排序的话,就建立一个大根堆
{
for(int parent=(usesized-1-1)/2;parent>=0;parent--)
{
shit(usesized,parent);
}
}
public static void shit(int len,int parent)
{
int child=2*parent+1;
while(child<len)
{
if(child+1<len&&elem[child]<elem[child+1])
{
child++;
}
if(elem[child]>elem[parent])
{
int tmp=elem[child];
elem[child]=elem[parent];
elem[parent]=tmp;
parent=child;
child=2*parent+1;
}
else
{
break;
}
}
public void paixu() {
while (usesized >= 1) {
int tmp1 = elem[0];
elem[0] = elem[usesized - 1];
elem[usesized - 1] = tmp1;
usesized--;
shit(usesized, 0);
}
}

3.交换排序:
(1)冒泡排序:
? ? 时间复杂度为O(N2)
? ? 空间复杂度为O(1)
? ? ?稳定性:稳定
??
public static void maopao(int[]arr)
{
int i=0;
for(i=0;i<arr.length-1;i++)
{
int j=0;
boolean a=false;
for(j=0;j<arr.length-1-i;j++)
{
if(arr[j]>arr[j+1])
{
swop(arr,j);
a=true;
}
}
if(a==false) //说明此时序列已经有序
{
return;
}
}
}? ?(2)快速排序
? ? ? ? ?时间复杂度:O(N)
? ? ? ? 空间复杂度:O(log2N)
? ? ? ? 稳定性:不稳定
? ? ? ? ? ? Hore版
? ? ? ? ?
先把6作为基准,R先从右边找比6大的,找到停下,然后L再从左边找,找到比6?小的,然后交换,然后R再找找完L再找,直到两者相遇,此时将相遇点的值和基准交换,此时我们可以观察到6的左边都是比6小的,6的右边都是比6大的,然后我们分而治之


直到l r重合,返回。

public static void qiuklysort(int[]arr,int left,int right)
{
if(left>=right)
{
return;
}
int pre=find1(arr,left,right);
qiuklysort(arr,left,pre-1);
qiuklysort(arr,pre+1,right);
}
public static int find1(int[]arr,int left,int right)
{
int tmp=arr[left];
while(left<right)
{
while(left<right&&arr[right]>=tmp)
{
right--;
}
arr[left]=arr[right];
//left++; //注意这里的left下面的right--,一旦加上了就不存可能永不相遇的情况
while(left<right&&arr[left]<=tmp)
{
left++;
}
arr[right]=arr[left];
//right--;
}
arr[left]=tmp;
return left;
}?2.挖孔法:



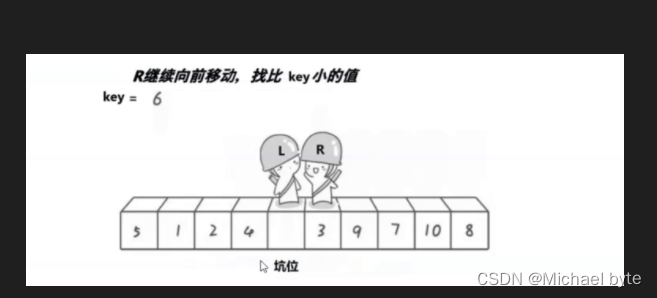


最后相遇的时候把6在放入这个坑位。
public static void quklysort2(int[]arr,int left,int right)
{
if(left>=right)
{
return;
}
int b= findmid(arr,left,right);
//int tmp=arr[b];
//arr[b]=arr[left];
//arr[left]=tmp;
int pre=find1(arr,left,right);
quklysort2(arr,left,pre-1);
quklysort2(arr,pre+1,right);
}
public static int find1(int[]arr,int left,int right)
{
int tmp=arr[left];
while(left<right)
{
while(left<right&&arr[right]>=tmp)
{
right--;
}
arr[left]=arr[right];
//left++;
while(left<right&&arr[left]<=tmp)
{
left++;
}
arr[right]=arr[left];
//right--;
}
arr[left]=tmp;
return left;
}?我们在解题的时候先考虑挖坑法,再用Hore版
快排的优化
我们知道数据是越来越有序的,那么我们如果在递归多的区间进行选择排序,那么快排就会变快

像这个其实递归多的地方主要在下边?
public static void quklysort4(int[]arr,int left,int right)
{
if(left>=right)
{
return;
}
if(right-left>=2)
{
selectsort3(arr,left,right);
}
int pre=find1(arr,left,right);
qiuklysort(arr,left,pre-1);
qiuklysort(arr,pre+1,right);
}
像这样一组数据,我们如果还是始终以第一个数据为基准的话,就会排成这样

时间复杂度也会变为O(N2),空间复杂度会变为O(N)那么什么办法去解决这个问题吗?
我们用三数取中法来解决这个问题:

我们将left 、right? 以及? (left+right?)/2下标的数值进行比较,找到第二个大的数将它作为基准,这样就可以使基准左右都有数据。
ublic static void quklysort2(int[]arr,int left,int right)
{
if(left>=right)
{
return;
}
int b= findmid(arr,left,right);
//int tmp=arr[b];
//arr[b]=arr[left];
//arr[left]=tmp;
int pre=find1(arr,left,right);
quklysort2(arr,left,pre-1);
quklysort2(arr,pre+1,right);
}
public static int findmid(int[]arr,int left,int right)
{
int mid=(left+right)/2;
if(arr[left]>arr[right])
{
if(arr[mid]<arr[left])
{
return right;
}
else if(arr[mid]>arr[left])
{
return left;
}
else
{
return mid;
}
}
else
{
if(arr[mid]<arr[left])
{
return left;
}
if(arr[mid]>arr[right])
{
return right;
}
return mid;
}
}?快排的非递归方法
建立一个栈,排序找基准,然后将基准两侧的left,right分别放入栈中,(这里要注意当基准一侧只有一个元素时,说明基准的这一侧已经有序,这一侧的left和right不需要再放入栈中),然后每次再弹出两个坐标,再后再排序,找基准再将基准放入栈中,再弹出,以此类推,直到栈为空

?
public static void fei(int[]arr)
{
Stack<Integer>stack=new Stack<>();
int left=0;
int right=arr.length-1;
int mid=find(arr,left,right);
if(left<mid-1)
{
stack.push(left);
stack.push(mid-1);
}
if(mid<right-1)
{
stack.push(mid+1);
stack.push(right);
}
while(!stack.isEmpty())
{
right=stack.pop();
left=stack.pop();
mid=find(arr,left,right);
if(left<mid-1)
{
stack.push(left);
stack.push(mid-1);
}
if(mid<right-1)
{
stack.push(mid+1);
stack.push(right);
}
}
}
public static int find(int[]arr,int left,int right)
{
int tmp=arr[left];
int i=left;
while(left<right)
{
while(left<right&&arr[right]>=tmp)
{
right--;
}
while(left<right&&arr[left]<=tmp)
{
left++;
}
swop(arr,left,right);
}
swop(arr,left,i);
return left;
}
public static void swop(int[]arr,int left,int right)
{
int tmp=arr[left];
arr[left]=arr[right];
arr[right]=tmp;
}?归并排序:
时间复杂度O(N*logN)
空间复杂度O(N)
稳定性:稳定



合并排序的思路就是:先把序列一步步的分解,分解成单个,然后再返回,再将子序列逐步地排序
最后就能形成有序的序列
//归并public static void fen(int[]arr,int left,int right)
{
if(left==right)
{
return ;
}
int mid=(left+right)/2;
fen(arr,left,mid);
fen(arr,mid+1,right);
paixu(arr,left,mid,right);
}
public static void paixu(int[]arr,int left,int mid,int right)
{
int[]arr2=new int[right-left+1];
int i=left;
int j=mid+1;
int k=0;
while(i<=mid&&j<=right)
{
if(arr[i]<=arr[j])
{
arr2[k++]=arr[i++];
}
else
{
arr2[k++]=arr[j++];
}
}
while(i<=mid)
{
arr2[k++]=arr[i++];
}
while(j<=right)
{
arr2[k++]=arr[j++];
}
for(i=0;i<k;i++)
{
arr[i+left]=arr2[i];
}
}不用比较的排序:
计数数组:(适用于集中的数)
举个例子假设有一个数组arr里面都是0-9的数,那么如果我们再定义一个大小为10的数组,然后把arr里面的每个数当成计数数组的下标,计数数组每次下标相同时这个下标元素的值都要加加
假设int[]arr={0,0,1,3,2,1,4,5,5,5,6,7,8,9};
我们在定义一个计数数组

?
每个count[i]都表示arr数组这个下标的元素有几个,这样我们就按照下标训序打印,但是注意个数,比如0 有两个,就打印两次
//计数排序public static void count(int[]arr)
{
int i=0;
int min=arr[0];
int max=arr[0];
for(i=1;i<arr.length;i++)
{
if(arr[i]<min)
{
min=arr[i];
}
if(arr[i]>max)
{
max=arr[i];
}
}
int size=max-min+1; //确定计数数组的大小
int[]arr2=new int[size];
for(i=0;i<arr.length;i++)
{
arr2[arr[i]-min]++;//处理如果数据不是0-9这样类似的数据,这时让每个数据减去最小值就0k
}
for(i=0;i<size;i++)
{
while(arr2[i]>=1)
{
System.out.print(i+min+" ");//打印的时候再加上min就变成原数了
arr2[i]--;
}
}
}

?
??