题目所属分类
传统的中序遍历 递归
和 必要背过的(Morris-traversal) O(n)算法
原题链接
给你二叉搜索树的根节点 root ,该树中的 恰好 两个节点的值被错误地交换。请在不改变其结构的情况下,恢复这棵树 。
代码案例:
输入:root = [1,3,null,null,2]
输出:[3,1,null,null,2]
解释:3 不能是 1 的左孩子,因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。
题解
常用解法
时间复杂度 O(n)
空间复杂度 O(n)

/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
List<TreeNode> list = new ArrayList<>();
public void dfs(TreeNode root){
if(root != null){
dfs(root.left);
list.add(root);
dfs(root.right);
}
}
public void recoverTree(TreeNode root) {
dfs(root);
TreeNode a = null;
TreeNode b = null;
for(int i = 0 ; i < list.size()-1 ; i++){
if(list.get(i).val > list.get(i+1).val){
b = list.get(i+1);
if(a == null){
a = list.get(i);
}
}
}
int t = a.val;
a.val = b.val;
b.val = t ;
}
}
空间复杂度为常数的解法
核心就是 当前左子树无右儿子的点指向root点
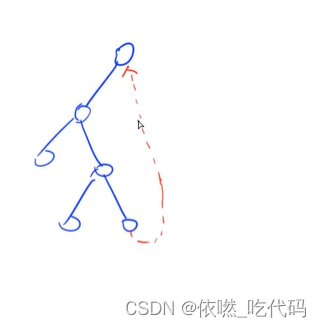
这里的y总的题解
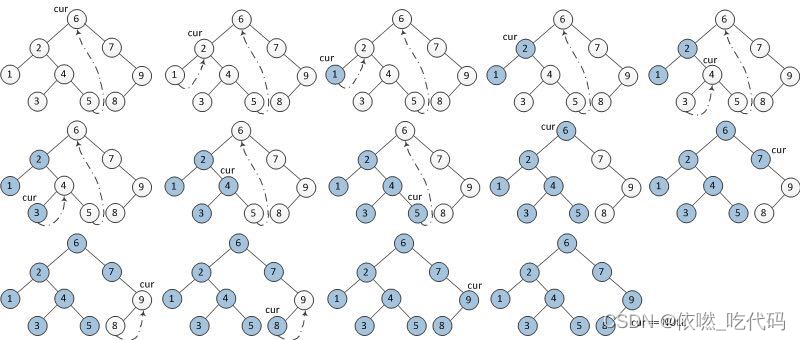
从根节点开始遍历,直至当前节点为空为止:
如果当前节点没有左儿子,则打印当前节点的值,然后进入右子树;
如果当前节点有左儿子,则找当前节点的前驱。
(1) 如果前驱节点的右儿子为空,说明左子树没遍历过,则进入左子树遍历,并将前驱节点的右儿子置成当前节点,方便回溯;
(2) 如果前驱节点的右儿子为当前节点,说明左子树已被遍历过,则将前驱节点的右儿子恢复为空,然后打印当前节点的值,然后进入右子树继续遍历;
中序遍历的结果就是二叉树搜索树所表示的有序数列。有序数列从小到大排序,但有两个数被交换了位置。共有两种情况:
交换的是相邻两个数,例如 1 3 2 4 5 6,则第一个逆序对,就是被交换的两个数,这里是3和2;
交换的是不相邻的数,例如 1 5 3 4 2 6,则第一个逆序对的第一个数,和第二个逆序对的第二个数,就是被交换的两个数,这里是5和2;
找到被交换的数后,我们将它们换回来即可。


/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public void recoverTree(TreeNode root) {
TreeNode first = null ;
TreeNode second = null ;
TreeNode p = null ;
while(root != null){
if(root.left == null){//没有左子树
if(p != null && p.val > root.val){//有逆序对
//看是第几个逆序对
if(first == null){//第一个逆序对
first = p ; second = root ;
}else{//第二个逆序对的话
second = root;
}
}
p = root;
root = root.right;
}else{//有左子树
//找前驱节点
TreeNode q = root.left;
while(q.right != null && q.right != root )q = q.right;
//两种情况
if (q.right == null){
q.right = root ;
root = root.left;
}else{
q.right = null;
//遍历当前点
//**** */
if(p != null && p.val > root.val){//有逆序对
//看是第几个逆序对
if(first == null){//第一个逆序对
first = p ; second = root ;
}else{//第二个逆序对的话
second = root;
}
}
//****** */
p = root ;
root = root.right;
}
}
}
int t = first.val;
first.val = second.val;
second.val = t ;
}
}