给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
?
示例 1:
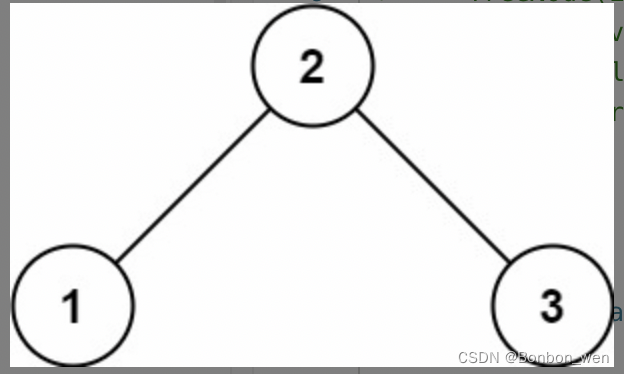
输入:root = [2,1,3]
输出:true
示例 2:
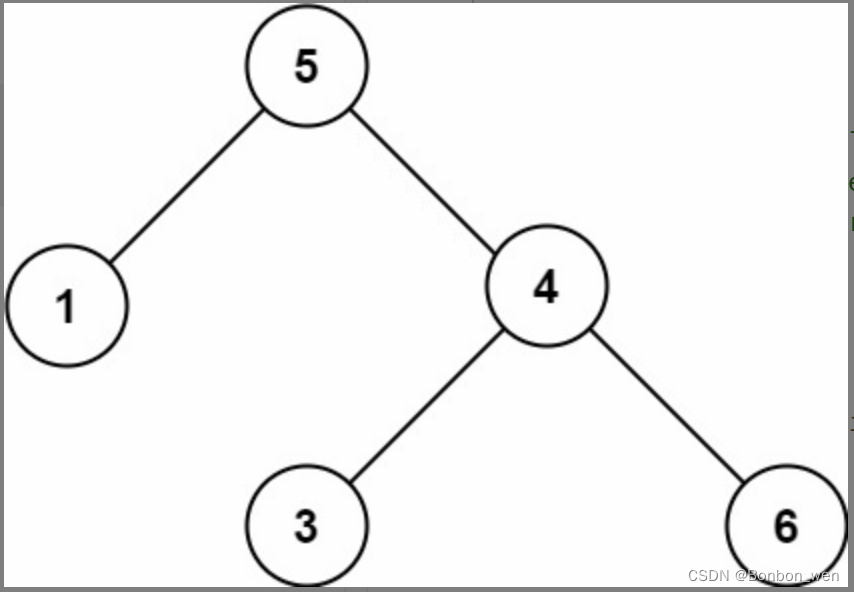
输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
?
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/validate-binary-search-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
class Solution {
TreeNode pre = null;
public boolean isValidBST(TreeNode root) {
// return isValidBSTI(root);
// return isValidBSTII(root);
return isValidBSTIII(root);
}
//方法三:与方法二类似,不过这里使用栈实现中序遍历
//时间和空间复杂度O(N)
private boolean isValidBSTIII(TreeNode root) {
if (root == null) {
return true;
}
Stack<TreeNode> stack = new Stack<>();
while (!stack.isEmpty() || root != null) {
while (root != null) {
stack.push(root);
root = root.left;
}
root = stack.pop();
if (pre != null && root.val <= pre.val) {
return false;
}
pre = root;
root = root.right;
}
return true;
}
//方法二:利用中序遍历升序特点,时间和空间复杂度O(N)
private boolean isValidBSTII(TreeNode root) {
if (root == null) {
return true;
}
if (!isValidBST(root.left)) {
return false;
}
if (pre != null && root.val <= pre.val) {
return false;
}
pre = root;
return isValidBST(root.right);
}
//方法一:利用最大值和最小值,时间和空间复杂度O(N)
//思考单独某一节点需要做什么?
//判断当前节点的左孩子值是否小于当前节点值 和 右孩子值是否大于当前节点值
//同时需要整个左子树都要满足小于当前节点值,整个右子树都要满足大于当前节点值
private boolean isValidBSTI(TreeNode root) {
if (root == null) {
return true;
}
return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);
}
private boolean isValidBST(TreeNode root, long min, long max) {
if (root == null) {
return true;
}
if (root.val <= min || root.val >= max) {
return false;
}
//左子树最大值是root.val,右子树最小值是root.val
return isValidBST(root.left, min, root.val) && isValidBST(root.right, root.val, max);
}
}