目录
1.随机快速排序算法
基本思想:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
随机快速排序算法核心和快速排序算法的区别在于对主元(pivot)选择上的随机性。每次选择pivot的时候,均在该部分的所有元素当中均匀随机的选择,每个元素被选择成为pivot的概率相等,想了解详细过程可以参考快速排序算法。
代码实现:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAXSIZE 10
//从范围p到r内找一个下标i,把这个数换到最左边,再进行快速排序Partition。
int RandomizedPartition(int a[],int p,int r)
{
srand(time(NULL));
int i = rand()%(r-p)+p;
Swap(a,i,p);
return Partition(a,p,r);
}
void RandomizedQuickSort(int a[],int p,int r)
{
if(p<r)
{
int q = RandomizedPartition(a,p,r);
RandomizedQuickSort(a,p,q-1);
RandomizedQuickSort(a,q+1,r);
}
}
void Swap(int a[],int left,int right)
{
int tmp;
tmp = a[left];
a[left] = a[right];
a[right] = tmp;
}
int Partition(int a[],int p,int r)
{
int i=p,j=r+1;
//本代码的主元选择的是p到r范围内的最左边的即p下标的数
int x = a[p];
while(1)
{
//将i和j一个从左,一个从右开始相向而行,使得在相遇之前,i部分都是小于x的数,j部分都是大于x的数。左右找到不匹配的数就互换值。
while(a[++i]<x && i<r) ;
while(a[--j]>x) ;
if(i>=j) break;
Swap(a,i,j);
}
//最后把p和j的下标互换一下就可以保证p到r范围内的数,a[j]左边都是小于a[j],右边都是大于a[j],但不代表左边有序或者右边有序,只是单纯的比a[j]小或大在一边而已
a[p]=a[j];
a[j]=x;
return j;
}
void QuickSort(int a[],int p,int r)
{ //p,r为边界,先处理左边再处理右边
if(p<r)
{
int q = Partition(a,p,r);
QuickSort(a,p,q-1);
QuickSort(a,q+1,r);
}
}2.非递归快速排序算法
非递归实现快速排序算法可以解决因递归会建立函数栈帧,从而递归的深度越深,占用栈区的空间就越大。而出现当深度足够深时,栈区的空间就会被用完,导致栈溢出的问题。
非递归快速排序算法就是利用循环了再次调用该函数的功能,也就是单趟排序,只要满足循环条件,就一直循环下去,我们可以利用数据结构中的栈来把每一次循环的参数记录下来,供单趟排序使用。
如图分析:
通过上次的学习我们知道了栈的特性是先进后出,我们拿数组arr=[5,2,4,7,9,1,3,6]来当例子。
第一步:我们先把区间的右边界值7进行压栈,然后把区间的左边界值0进行压栈,那我们取出时就可以先取到左边界值,然后取到右边界值。
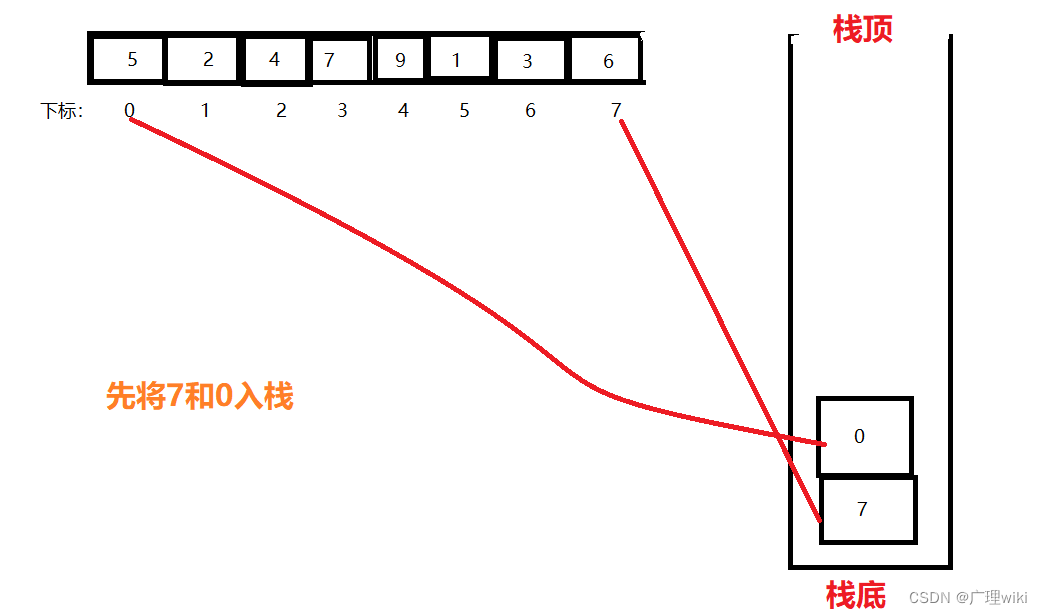
第二步:我们获取栈顶元素,先取到0给left,后取到7给right,进行单趟排序
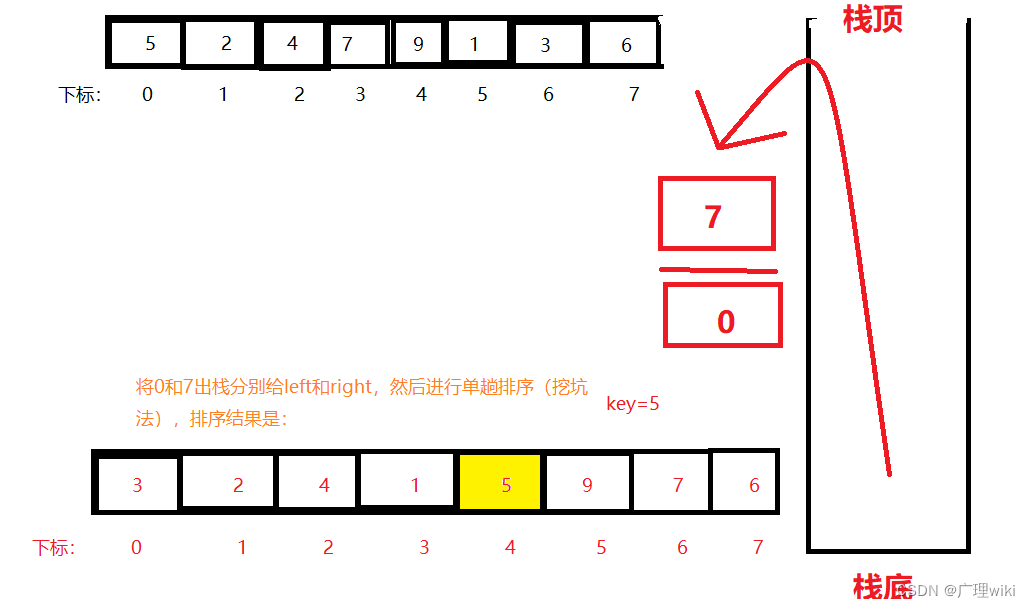
?第三步:第一趟排完后,区间被分为左区间和右区间。因为要先处理左区间,所以我们先将右区间压栈,分别压入7和5,然后压入左子区间,3和0。
?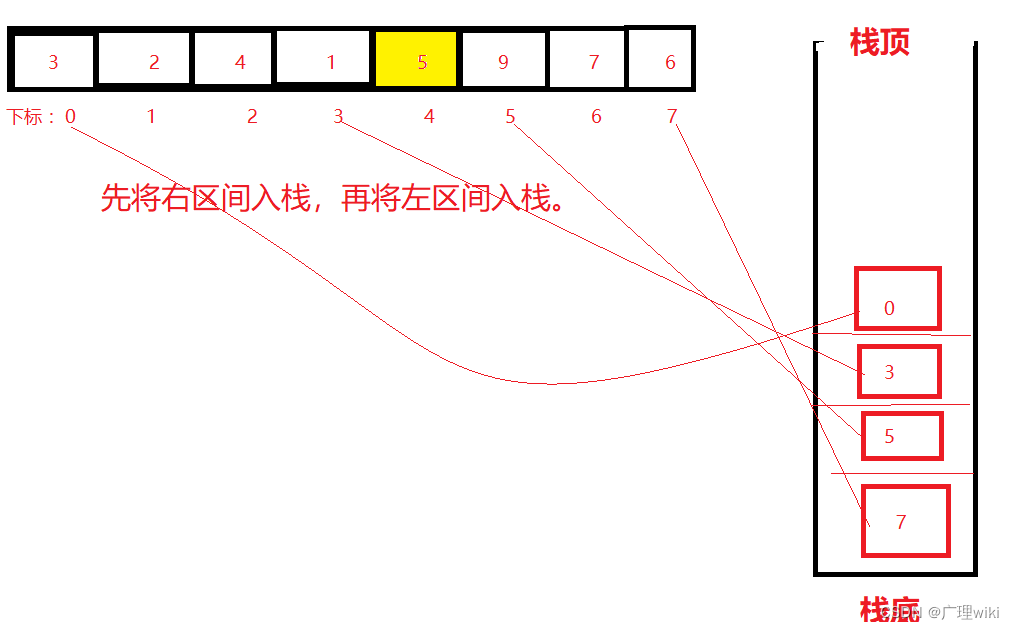
第四步:将0和3出栈后进行单趟排序。
?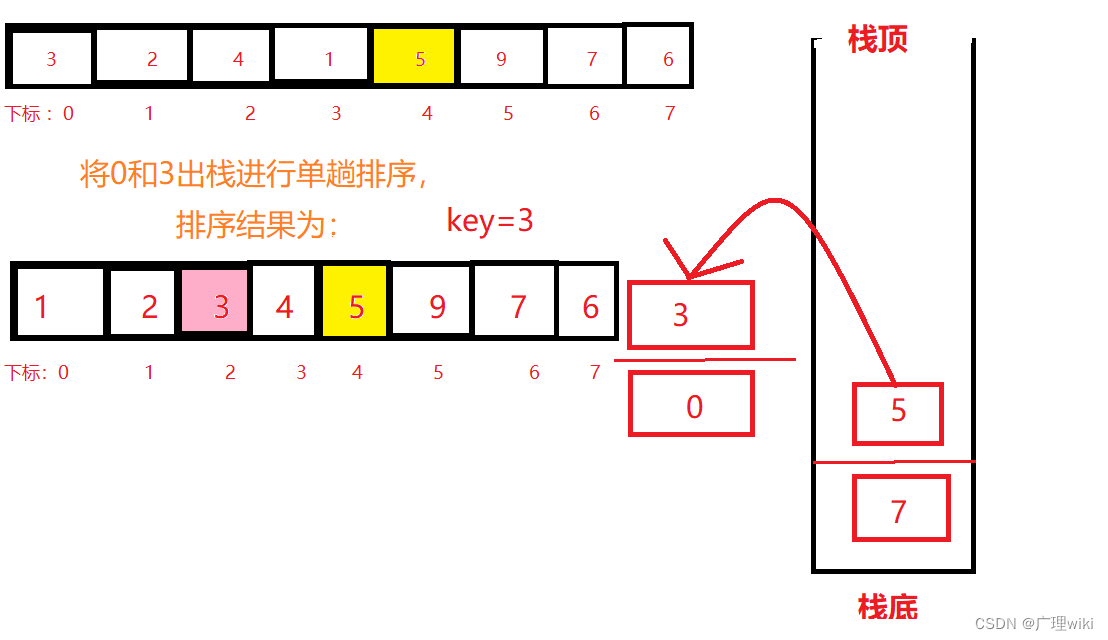
?第五步:此时左子区间又被划分为左右两个子区间,但是右子区间只有4一个值,不再压栈,所以只入左子区间,将1和0压栈。
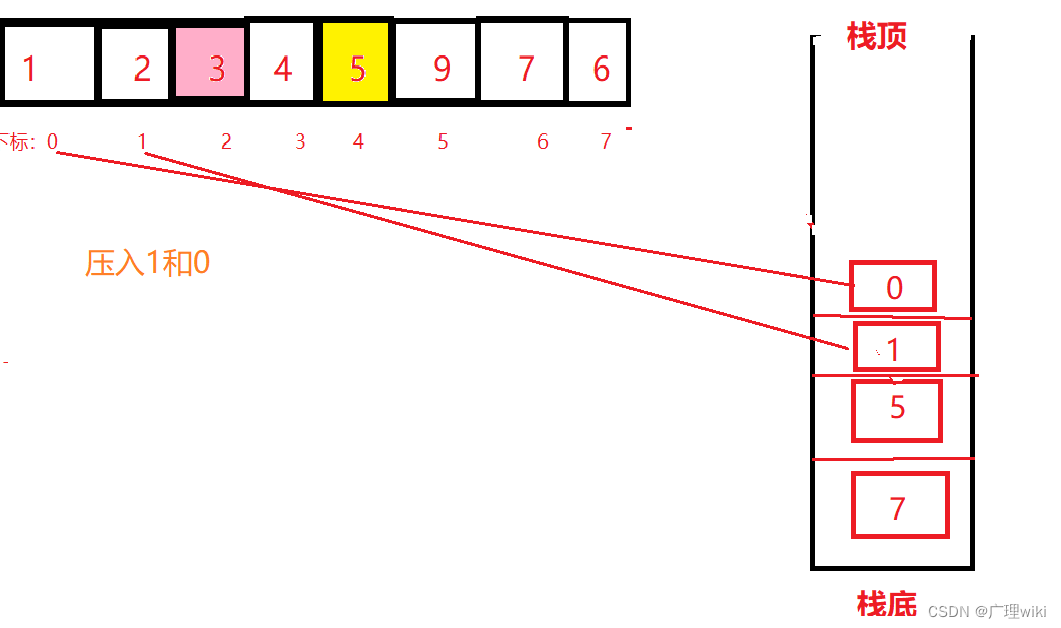
第六步:将0和1出栈后进行单趟排序.
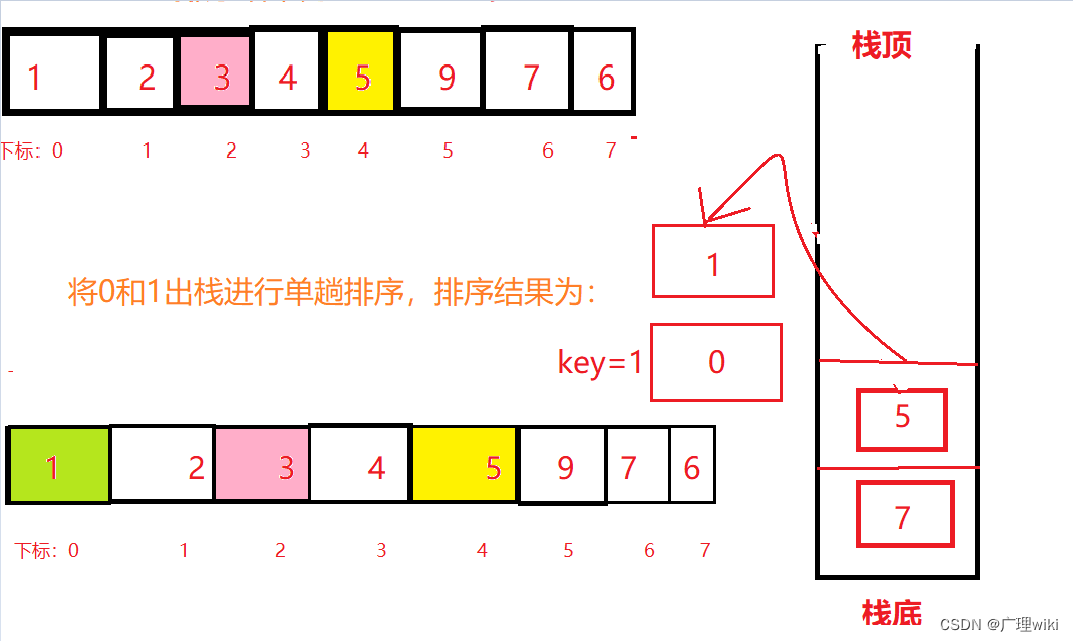
?第七步:第六步结束后,左区间全部被排完,这时候才来排右区间将5和7出栈后进行单趟排序,这个流程其实和递归是一模一样的,顺序也没变,但解决了递归的致命缺陷——栈溢出。后面的流程就按照上面排左区间的方法来排序。
代码实现:
//快排非递归
void QuickSort(int* arr, int n)
{
ST st;
StackInit(&st);
//把左右区间压栈,先压右边
StackPush(&st, n - 1);
//后压左边
StackPush(&st, 0);
//只要栈不为空,就继续分割排序
while (!StackEmpty(&st))
{
//从栈里面取出左右区间
int left = StackTop(&st);
StackPop(&st);
int right = StackTop(&st);
StackPop(&st);
int index = GetMinIndex(arr, left, right);
//因为我们下面的逻辑都是把第一个数作为key,
//为了避免改动代码,这里我们直接交换就可以
Swap(&arr[left], &arr[index]);
//开始单趟排序
int begin = left;
int end = right;
int pivot = begin;
int key = arr[begin];
while (begin < end)
{
//end开始找小
while (begin < end && arr[end] >= key)
{
end--;
}
arr[pivot] = arr[end];
pivot = end;
//begin开始找大
while (begin < end && arr[begin] <= key)
{
begin++;
}
arr[pivot] = arr[begin];
pivot = begin;
}
pivot = begin;
arr[pivot] = key;
//区间分为[left,pivot-1]pivot[pivot+1,right]
//利用循环继续分割区间
//先入右子区间
if (pivot + 1 < right)
{
//说明右子区间不止一个数
//先入右边边界
StackPush(&st, right);
//再入左边边界
StackPush(&st, pivot+1);
}
//再入左子区间
if (left < pivot-1)
{
//说明左子区间不止一个数
//先入右边边界
StackPush(&st, pivot-1);
//再入左边边界
StackPush(&st, left);
}
}
StackDestory(&st);
}3.三数取中划分算法
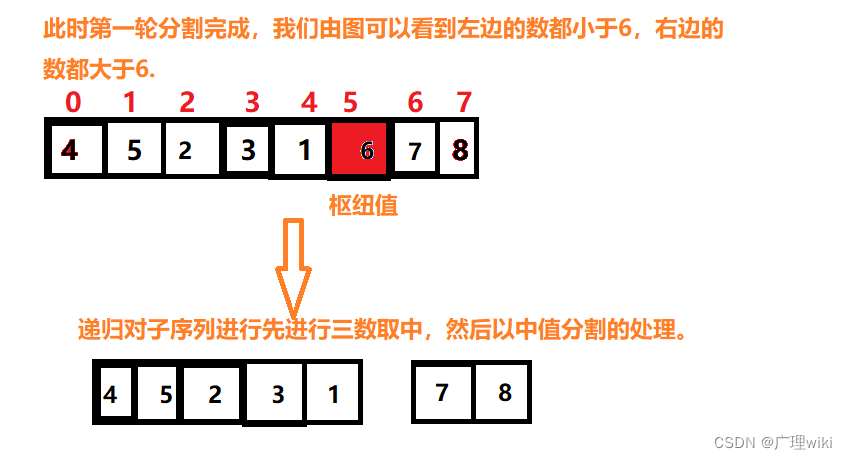
基本步骤:在快排的过程中,每一次我们要取一个元素作为枢纽值,以这个数字来将序列划分为两部分。在此我们采用三数取中法,也就是取左端、中间、右端三个数,然后进行排序,将中间数作为枢纽值,如图所示:
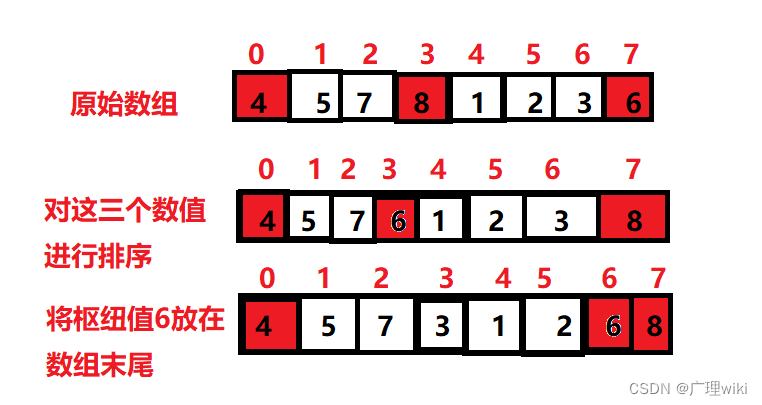
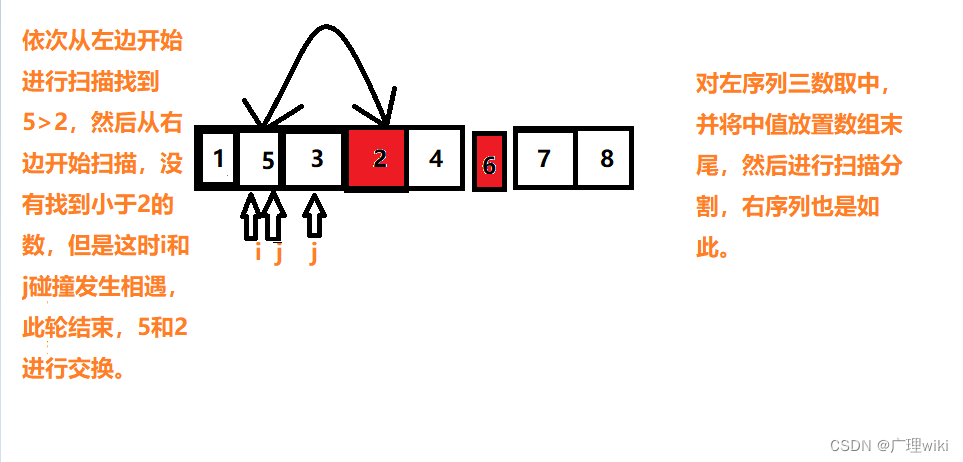
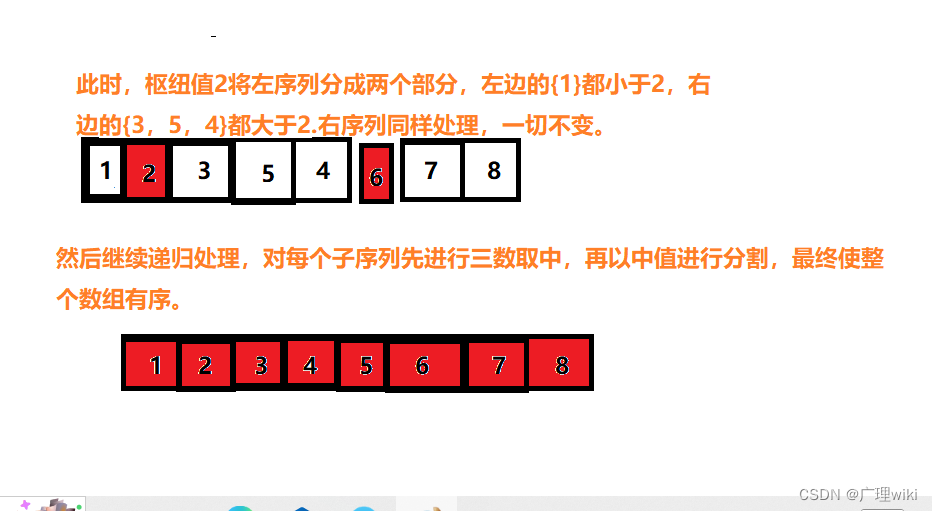
由枢纽值进行分割排序,如图所示:
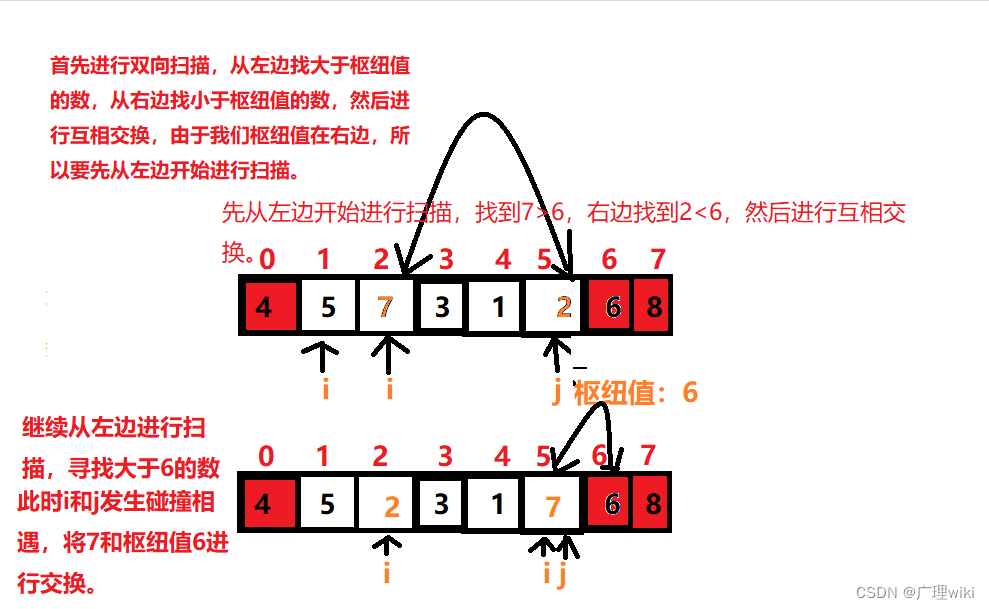
?
?
?
?代码实现:
package sortdemo;
import java.util.Arrays;
/**
* Created by chengxiao on 2016/12/14.
* 快速排序
*/
public class QuickSort {
public static void main(String[] args) {
int[] arr = {9, 8, 7, 6, 5, 4, 3, 2, 1, 0};
quickSort(arr, 0, arr.length - 1);
System.out.println("排序结果:" + Arrays.toString(arr));
}
/**
* @param arr
* @param left 左指针
* @param right 右指针
*/
public static void quickSort(int[] arr, int left, int right) {
if (left < right) {
//获取枢纽值,并将其放在当前待处理序列末尾
dealPivot(arr, left, right);
//枢纽值被放在序列末尾
int pivot = right - 1;
//左指针
int i = left;
//右指针
int j = right - 1;
while (true) {
while (arr[++i] < arr[pivot]) {
}
while (j > left && arr[--j] > arr[pivot]) {
}
if (i < j) {
swap(arr, i, j);
} else {
break;
}
}
if (i < right) {
swap(arr, i, right - 1);
}
quickSort(arr, left, i - 1);
quickSort(arr, i + 1, right);
}
}
/**
* 处理枢纽值
*
* @param arr
* @param left
* @param right
*/
public static void dealPivot(int[] arr, int left, int right) {
int mid = (left + right) / 2;
if (arr[left] > arr[mid]) {
swap(arr, left, mid);
}
if (arr[left] > arr[right]) {
swap(arr, left, right);
}
if (arr[right] < arr[mid]) {
swap(arr, right, mid);
}
swap(arr, right - 1, mid);
}
/**
* 交换元素通用处理
*
* @param arr
* @param a
* @param b
*/
private static void swap(int[] arr, int a, int b) {
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
}
4.三划分快速排序算法
基本思路:
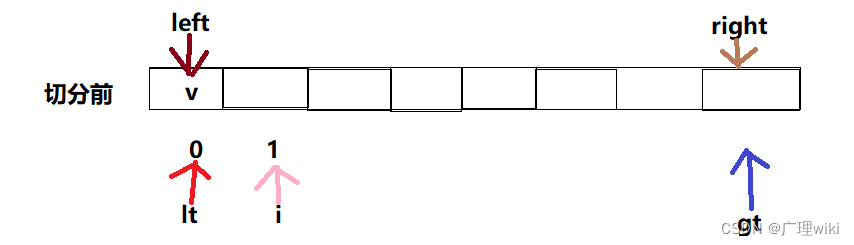
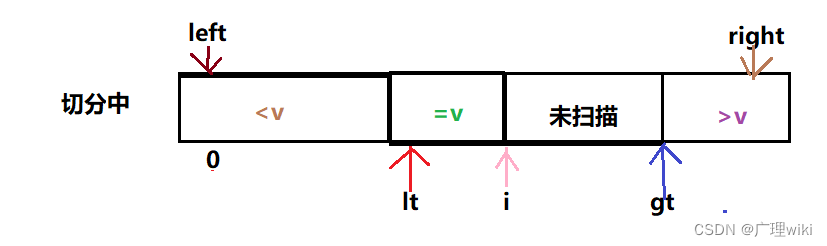
1.将数组分为三部分,分别对应的是小于、等于和大于哨兵元素v的子序列。
 ?
?
 ?
?
? ? ? ? ? ? ?
?
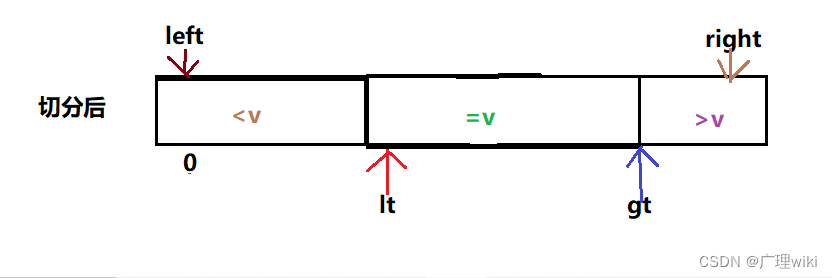
切分方法:从左到右扫描数组一次,首先用一个指针lt使得a[left..lt-1]中的元素都小于v,再用一个指针gt使得a[gt+1..right]中的元素都大于v,最后用一个指针i使得a[lt..i-1]中的元素都等于v,而a[i..gt]中的元素是还未扫描的。
算法一开始首先令i = left + 1,对a[i]与v进行比较,根据实际的比较情况进行不同的操作:
(1)a[i]小于v,将a[lt]和a[i]交换,将lt++和i++;
(2)a[i]大于v,将a[gt]和a[i]交换,将gt--;
(3)a[i]等于v,将i++;
通过以上的操作就会不断缩小gt - i的值,直到i > gt扫描结束。在这时完成了数组的切分就如上图所示的切分后的样子了。
讲到这里相信大家都对三划分快速排序算法有了粗略的了解了吧,接下来我就讲讲一个例子吧。
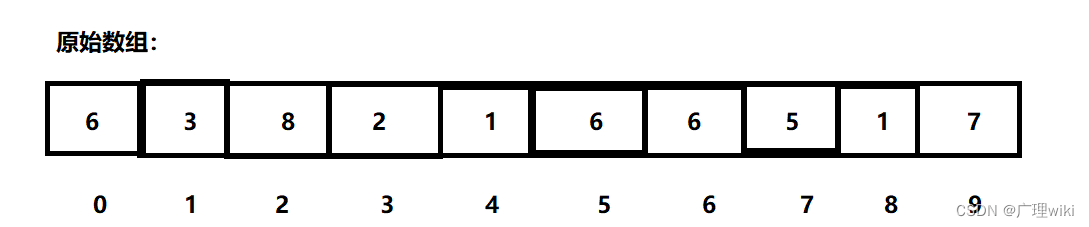
1.使这三个指针就位。我们选取的哨兵元素v为6。
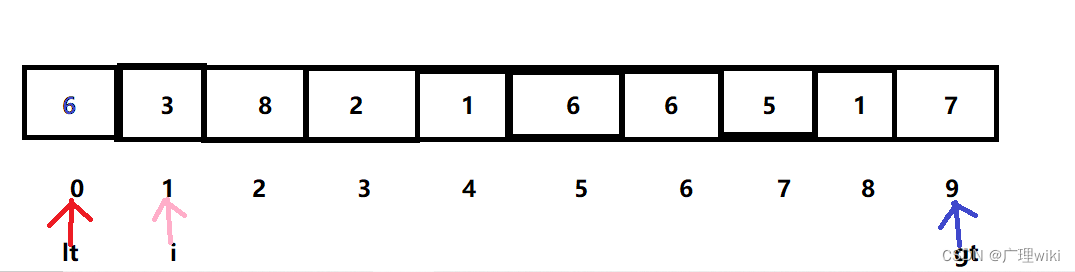
2.因为a[i]=3小于6,所以交换a[lt]和a[i]:6和3,lt和i指针后移。
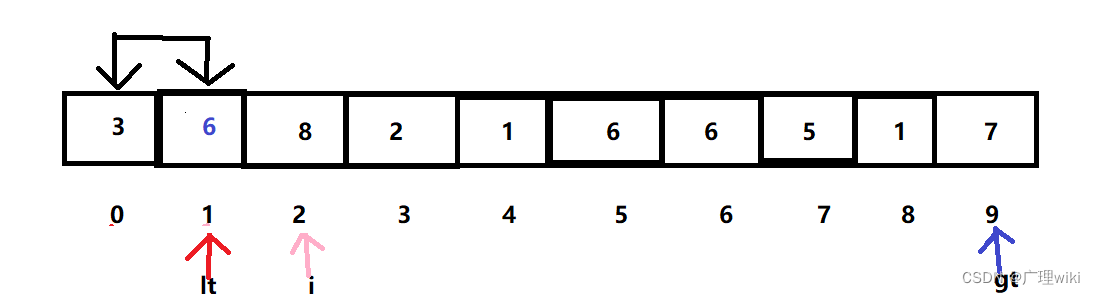
3.因为a[i]=8大于6,所以交换a[gt]和a[i]:7和8,gt指针前移。
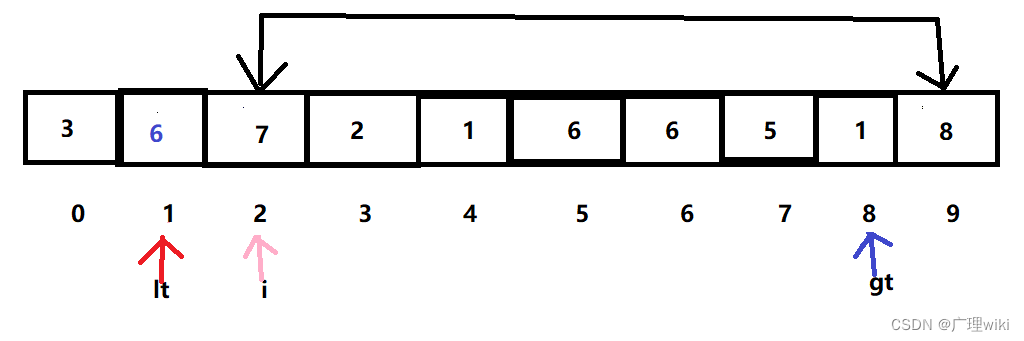
?4.因a[i]=7大于6,所以交换a[gt]和a[i]:1和7,gt指针前移。
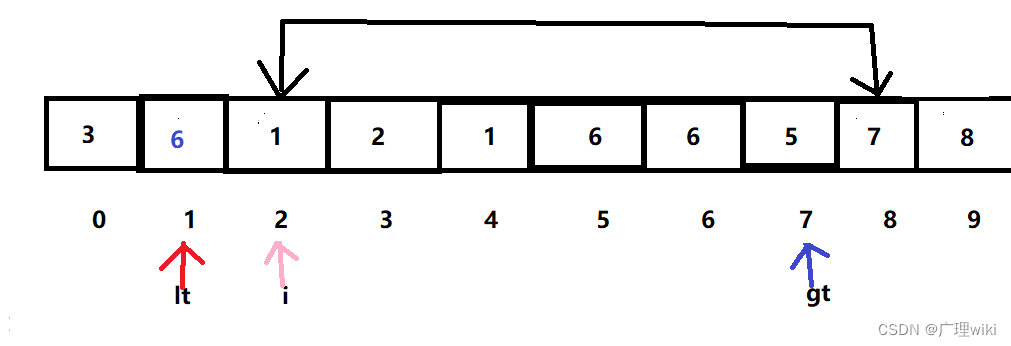
5.因为.a[i]=1小于6,所以交换a[lt]和a[i]:6和1,lt和i指针后移。

6.因a[i]=2小于6,所以交换a[lt]和a[i]:6和2,lt和i指针后移。
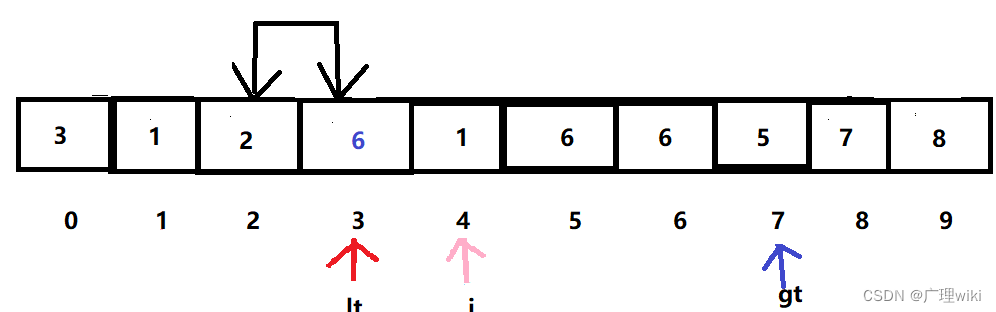
7.因a[i]=1小于6,所以交换a[lt]和a[i]:6和1,lt和i指针后移。
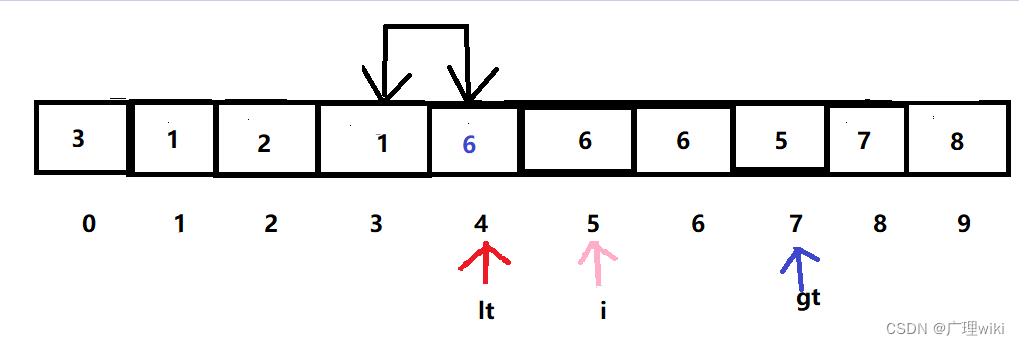
8.因为a[i]=6等于6,所以i指针后移。直到a[i]=5,交换6和5,lt和i指针后移,然后不满足i <= gt的条件啦,跳出循环。

9.这样数组就被分为三部分,分别对应于小于、等于和大于哨兵元素v的子序列。一次切分就完成了,接下来只要对小于和大于v的部分进行同样的切分即可。
代码实现:
private static <E extends Comparable<? super E>> void quick3Way(E[] a) {
shuffle(a);
quick3Way(a, 0, a.length - 1);
}
/**
* @param a
* @param left
* @param right
* @param <E>
*/
private static <E extends Comparable<? super E>> void quick3Way(E[] a, int left, int right) {
if (right <= left) {
return;
}
int lt = left, i = left + 1, gt = right;
E v = a[left];
//当 i > gt时跳出循环
while (i <= gt) {
int cmp = a[i].compareTo(v);//这里有个坑,注意和普通快排算法不一样,a[left]的元素是会发生变化的,因此需要用临时变量v缓存起来,compareTo函数是用于比较两个数的大小
if (cmp < 0) {
//a[i]小于v,将a[lt]和a[i]交换,将lt和i加1;
swap(a, lt++, i++);
} else if (cmp > 0) {
//a[i]大于v,将a[gt]和a[i]交换,将gt减1;
swap(a, gt--, i);
} else {
//a[i]等于v,将i加1
i++;
}
}
quick3Way(a, left, lt - 1);
quick3Way(a, gt + 1, right);
}5.合并排序算法?
合并排序归根到底就是采用分治法,先将无序序列划分为有序子序列,然后再将有序子序列合并成一个有序序列的排序算法。
?基本思想:首先将无序序列利用二分法划分为子序列,直到每个子序列只有一个元素(单元素序列必有序),然后再对有序子序列两两进行合并排序。而合并方法是循环地将两个有序子序列的首元素来进行比较,将其中较小的元素取出,放在合并序列的左边空位,直到其中一个子序列的最后一个元素放到合并序列中。最后将另一个子序列的剩余元素按顺序逐个放到合并序列尾部之后就完成了合并排序。
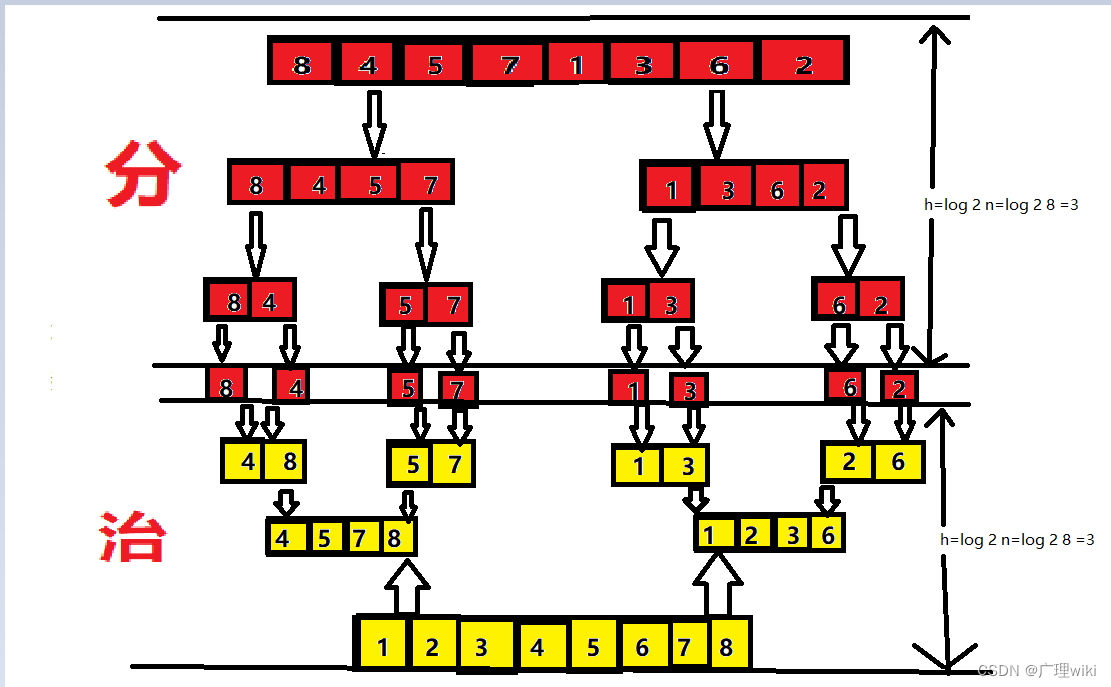
整个过程如下面动图所示:
? ?? ?
?
代码实现:
#include <malloc.h>
#include <stdlib.h>
void mergesort(int A[],int n) //合并排序的递归主体
{
void merge(int A[], int L[], int R[], int l, int r); //声明merge函数
if(n>1) //多于一个元素才需要排序
{
int mid=n/2;
int *left=(int*)malloc(sizeof(int)*mid);
int *right=(int*)malloc(sizeof(int)*(n-mid));
for(int i=0;i<mid;i++)
left[i]=A[i]; //建立临时数组存储左半部分序列
for(int j=mid;j<n;j++)
right[j-mid]=A[j]; //建立临时数组存储右半部分序列
mergesort(left,mid); //调用自身对左半部分进行合并排序
mergesort(right,n-mid); //调用自身对右半部分进行合并排序
merge(A,left,right,mid,n-mid); //两个有序序列的合并操作,封装为函数
free(left);
free(right);
}
}
void merge(int A[],int L[],int R[],int l,int r) //两个有序序列L、R合并为A,l,r分别为L,R的长度
{
int i=0,j=0,k=0;
while(i<l&&j<r) //两个子序列首元素做比较,小者取出置入父序列
{
if(L[i]<=R[j])
A[k++]=L[i++];
else
A[k++]=R[j++];
}
while(i<l) //将左半部分剩余元素置入父序列
{
A[k++]=L[i++];
}
while(j<r) //将右半部分剩余元素置入父序列
{
A[k++]=R[j++];
}
}?补充:在我看来,自然合并排序算法与合并排序算法的区别在于对于初始给定的数组, 通常存在多个长度大于1的已自然排好序的子数组段,并且自然合并排序进行合并排序所需的合并次数较少。自底向上的合并排序算法与合并排序算法我个人认为基本都一样,没有太大的区别,只不过自底向上的合并排序算法就是将一个无序的N长数组切个成N个有序子序列,然后再两两合并,然后再将合并后的N/2(或者N/2 + 1)个子序列继续进行两两合并,以此类推得到一个完整的有序数组。(在这个过程中可能一开始就存在1个只有1个元素的有序子序列留到最后再排序合并成一个有序数组)