[数据结构与算法]LeetCode-494-目标和

1、回溯法

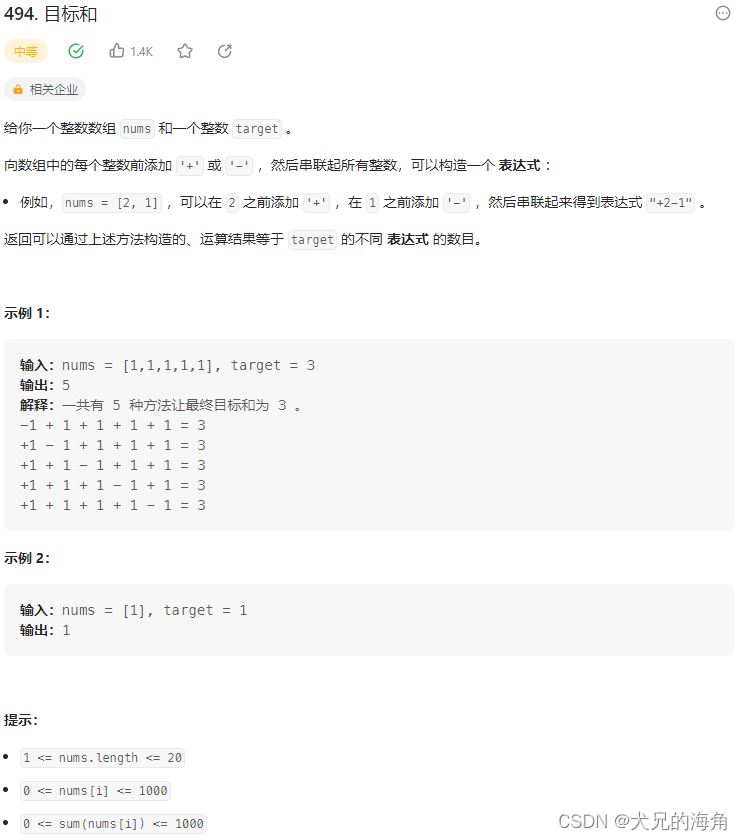
考虑到我们需要找到所有能够构成目标和的组合，因此我们可以采用深度遍历遍历每一种可能的数字组合最终获得一个值，我们最终比较这个值与目标和是否相等即可。

class Solution {
public:
    int dfs(vector<int> &nums, int target, int index, int temp_sum) {
        int count = 0;
        if (index >= nums.size()) {
            if (temp_sum == target) return ++count;
            else return 0;
        } else {
            count += dfs(nums, target, index + 1, temp_sum + nums[index]);
            count += dfs(nums, target, index + 1, temp_sum - nums[index]);
            return count;
        }
    }

    int findTargetSumWays(vector<int> &nums, int target) {
        int count = dfs(nums, target, 0, 0);
        return count;
    }
};

2、动态规划法

我们假设数组元素之和为$sum$，假设我们已经选定了添加负号的元素之和为$neg$，显然添加正号的元素之和为$sum?neg$。因此我们可以得到$(sum?neg)?neg=target$，因此$neg=(sum?target)/2$。因此我们可以将题目转化为从数组中找到n种能够将元素之和组合成$(sum?target)/2$的组合，是变形的01背包问题。

我们可以利用二维数组$dp[i][j]$用于记录我们能够使用前i个元素组合成j的组合数：1、当新增元素小于等于j时，我们可以选择新增元素也可以选择不新增元素；2、当新增元素大于j时，我们只能不新增元素。

class Solution {
public:
    int findTargetSumWays(vector<int> &nums, int target) {
        int sum = 0, n = nums.size(), neg;
        for (int i: nums) {
            sum += i;
        }
        if ((sum - target) < 0 || (sum - target) % 2 != 0) {
            return 0;
        }
        neg = (sum - target) / 2;
        vector<vector<int>> dp(n + 1, vector<int>(neg + 1));
        dp[0][0] = 1;
        for (int i = 1; i <= n; i++) {
            int num = nums[i - 1];
            for (int j = 0; j <= neg; j++) {
                dp[i][j] = dp[i - 1][j];
                if (j >= num) {
                    dp[i][j] += dp[i - 1][j - num];
                }
            }
        }
        return dp[n][neg];
    }
};

3、动态规划法优化

考虑到我们在01背包问题中只使用到了上一行的内容，因此我们在更新dp时可以只是用一个一维数组进行更新。值得注意的是，我们在更新时由于我们会使用到小于当前j的值，因此我们需要从后向前进行更新。

class Solution {
public:
    int findTargetSumWays(vector<int> &nums, int target) {
        int sum = 0, n = nums.size(), neg;
        for (int i: nums) sum += i;
        if ((sum - target) < 0 || (sum - target) % 2 != 0) return 0;
        neg = (sum - target) / 2;
        vector<int> dp(neg + 1);
        dp[0] = 1;
        for (int i = 1; i <= n; i++) {
            int num = nums[i - 1];
            for (int j = neg; j >= 0; --j) {
                if (j >= num) {
                    dp[j] += dp[j - num];
                }
            }
        }
        return dp[neg];
    }
};