[数据结构与算法]数据结构与算法--回溯算法(组合问题全解+模板方法)

代码随想录回溯–组合+组合总和问题全解+模板方法，如果没有了解递归的可以先看看上两篇文章

一:回溯算法理论知识详解

什么是回溯法：回溯法也叫做回溯搜索法，回溯和递归是一个意思，也可以说回溯就是递归，回溯和递归是一个函数，回溯并不是很高效的搜索方法，回溯的本质也就是穷举所有的情况列举出来，如果想要回溯算法的效率高一点，可以对其进行剪枝操作(也就是将有的不用搜索的情况给剪掉)。
回溯的所有问题都可以抽象成树形结构，回溯就是递归嘛，然后回溯肯定得有终止条件，所以回溯抽象成的树形结构树的高度必须是有限高度。因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度，都构成的树的深度。

如下图所示，就是标准的回溯问题图解也就是穷举每种情况，假如每次是找到两个数为子集的情况

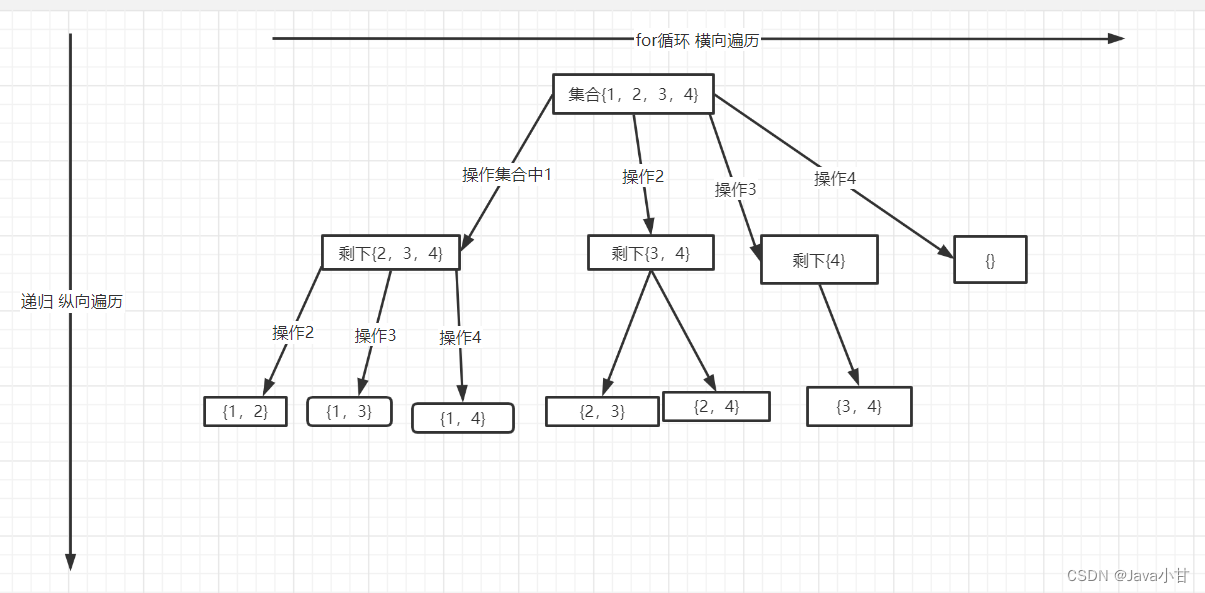
以此为例子，回溯问题也有模板方法

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

!然后还是不太理解的咱们接下来详细看题目解题思路

二：1.1组合问题

力扣题目77链接

思路图解：

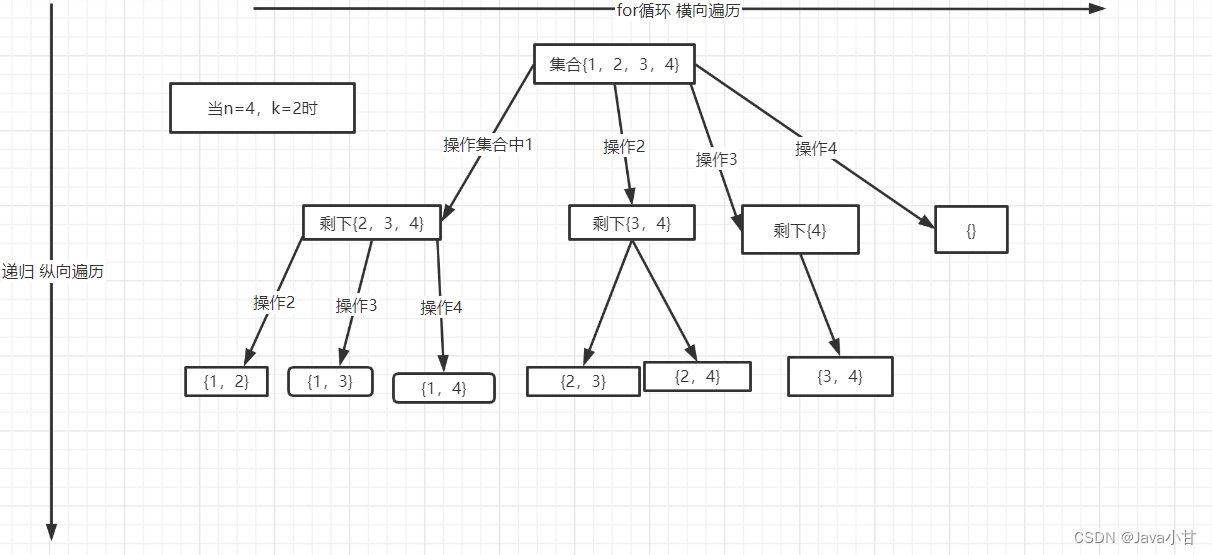
详细描述：由图所示，先用for遍历集合中的每个元素，遍历每个元素的时候将这个元素在进行深度递归的纵向遍历，就可以得到每种情况。比方说，第一次横向遍历，取1之后，集合剩下{2,3,4},再将{2,3,4]进行递归的纵向遍历，然后就能得到目标集合{1，2}，{1，3}，{1，4}，这就是第一次横向遍历加上纵向递归就能得出的结果。

//模板方法，大多数回溯问题都可以用这个模板
class Solution {
    List<List<Integer>> result=new ArrayList<>();//result集合用来存放数组集合
    LinkedList<Integer> path=new LinkedList<>();//用来存放每种结果
    public List<List<Integer>> combine(int n, int k) {
         combinehelper(n,k,1);
         return result;
    }
    public void combinehelper(int n,int k,int startindex){
        if(path.size()==k){//当path的大小等于目标个数，就将path存入result中
            result.add(new ArrayList(path));
            return; 
        }
        for(int i=startindex;i<=n;i++){//横向遍历，遍历数组集合中每个元素
            path.add(i);
            combinehelper(n,k,i+1);//递归纵向遍历
            path.removeLast();//进行回溯操作
        }
    }
}

1.2 组合优化（剪枝优化）

还是上个题目，假如n=4，k=3时候，这个例子好讲解一点，如下图所示

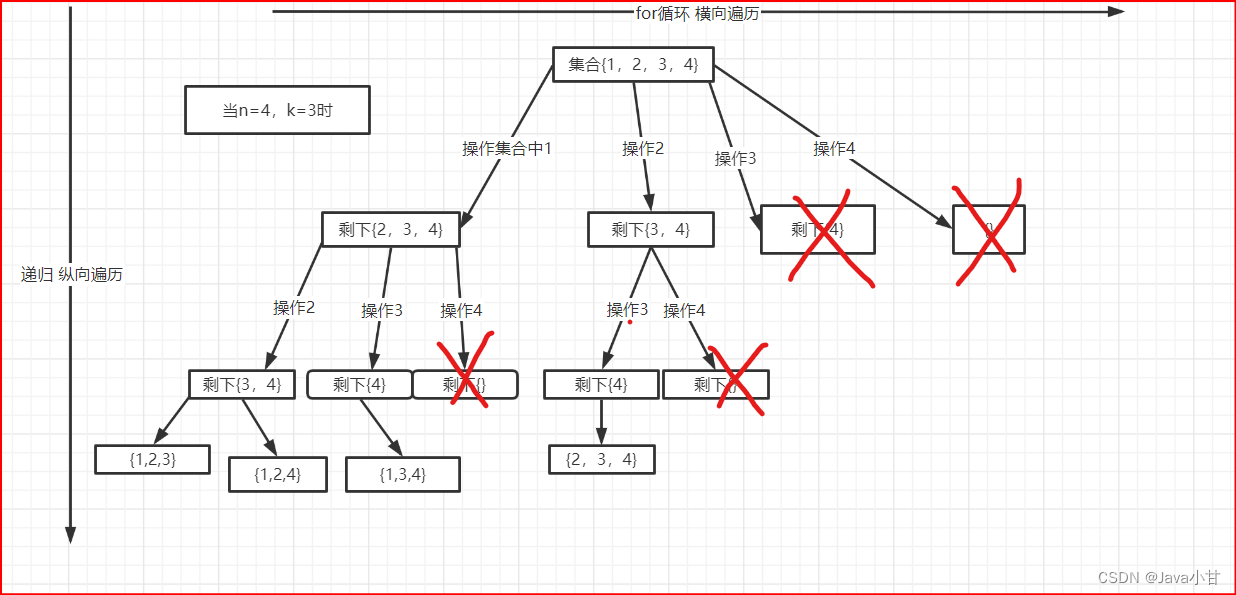
由上图所示，画×的都不用遍历了已经，因为遍历出来的结果也是不符合要求的，因此可以进行剪枝操作，从而提高算法的效率。

for(int i=startindex;i<=n;i++)从这儿优化
—> for(int i=startindex;i<=n-(k-path.size())+1;i++)
优化后的效果

三：组合总和Ⅲ

力扣216题目链接
找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

*只使用数字1到9
*每个数字 最多使用一次
*返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

提示:
2 <= k <= 9；
1 <= n <= 60；

图解思路：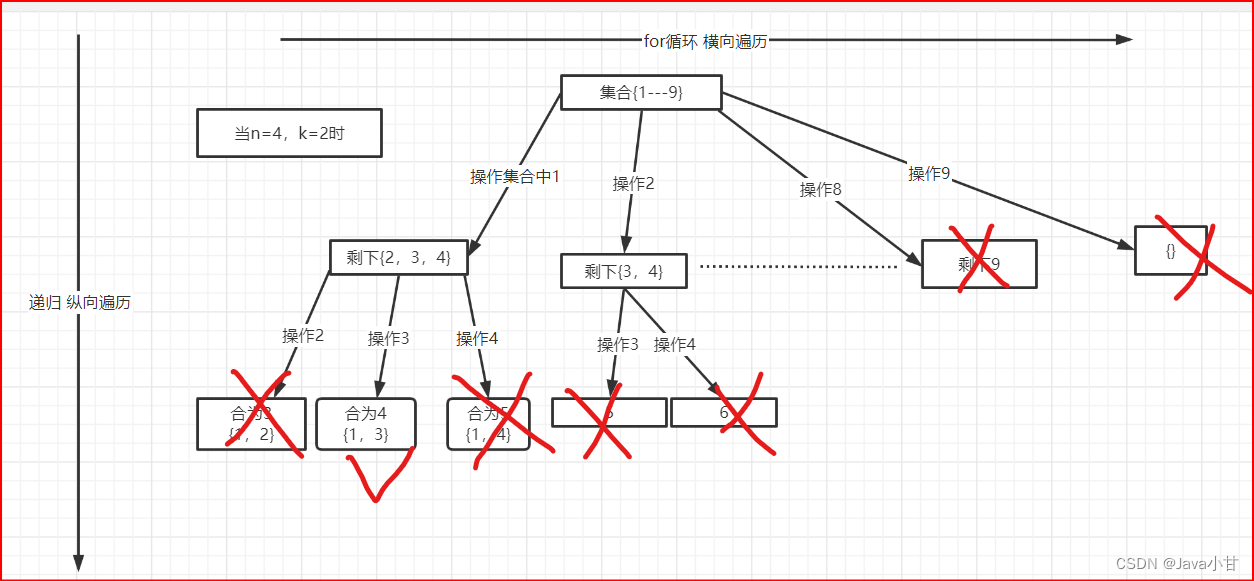
详细思路和上一题基本一样，也就是多了一个sum来计算和，直接用回溯的模板代码很快就写出来了，如下所示

class Solution {
    List<List<Integer>> result=new ArrayList<>();
    LinkedList<Integer>  path=new LinkedList<>();
    public List<List<Integer>> combinationSum3(int k, int n) {
            combinationSum1(k,n,1,0);
            return result;
    }
    public void combinationSum1(int k,int targetsum,int start,int sum){
        if(sum>targetsum) return;
        if(path.size()==k){
            if(sum==targetsum){
                result.add(new ArrayList(path));
            }
        }

        for(int i=start;i<=9-(k-path.size())+1;i++){
            path.add(i);
            sum+=i;//计算path里面的元素和
            combinationSum1(k,targetsum,i+1,sum);
            sum-=i;//进行回溯操作
            path.removeLast();//进行回溯操作
        }


    }
}

四：电话号码的字母组合

力扣17题目链接

思路图解：

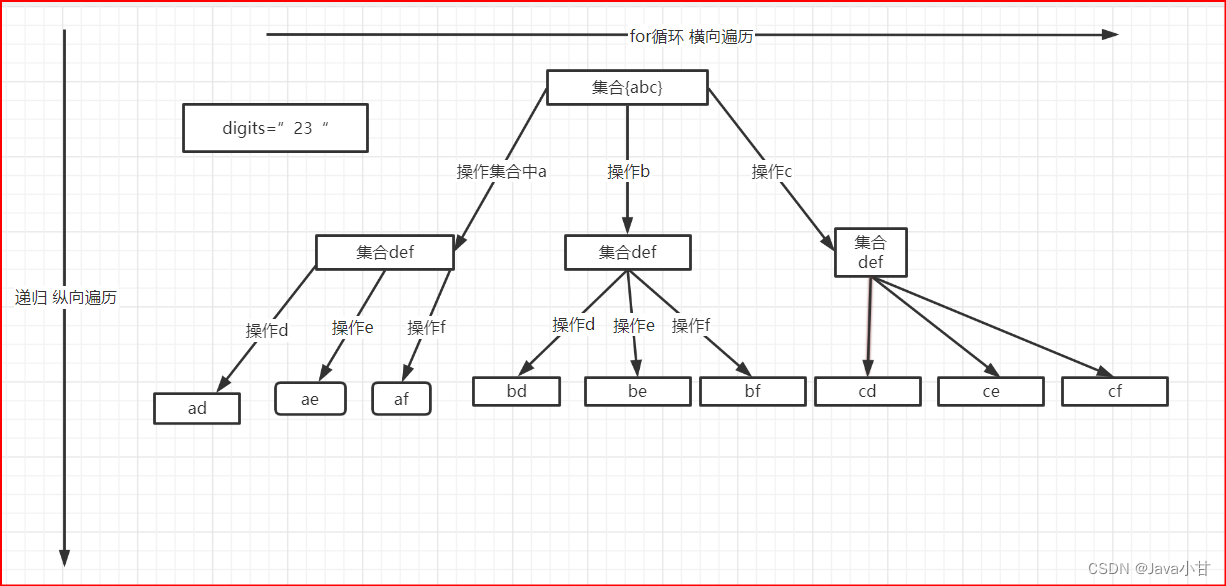
做题思路：先将题目中的2-9对应的字母表示出来，定义一个字符串数组，将数组中的索引对应到题目所示的对应关系，比如，索引2的位置就对应abc，然后再需要注意的就是将digits中的元素一个一个取出来，然后就进行操作，如下所示

class Solution {
    List<String> list=new ArrayList<>();
    StringBuilder temp=new StringBuilder();
    public List<String> letterCombinations(String digits) {
       if(digits==null||digits.length()==0) return list;
       String[] arr={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
       //这就是将题中的对应关系描述出来
       letterCombinations1(digits,arr,0);
       return list;
    }
    public void letterCombinations1(String digits,String[] arr,int startsum){
        if(startsum==digits.length()){
            list.add(temp.toString());
            return;
        }

        //String arr1=arr[digits.charAt(startsum)-'0'];
         String arr1 = arr[digits.charAt(startsum) - '0'];
        for(int i=0;i<arr1.length();i++){
            temp.append(arr1.charAt(i));
            letterCombinations1(digits,arr,startsum+1);
            temp.deleteCharAt(temp.length()-1);//进行回溯操作
        }
    }
}

这些个题大概意思都是差不多的，都可以用这个模板做

五：组合总和

力扣39题目链接

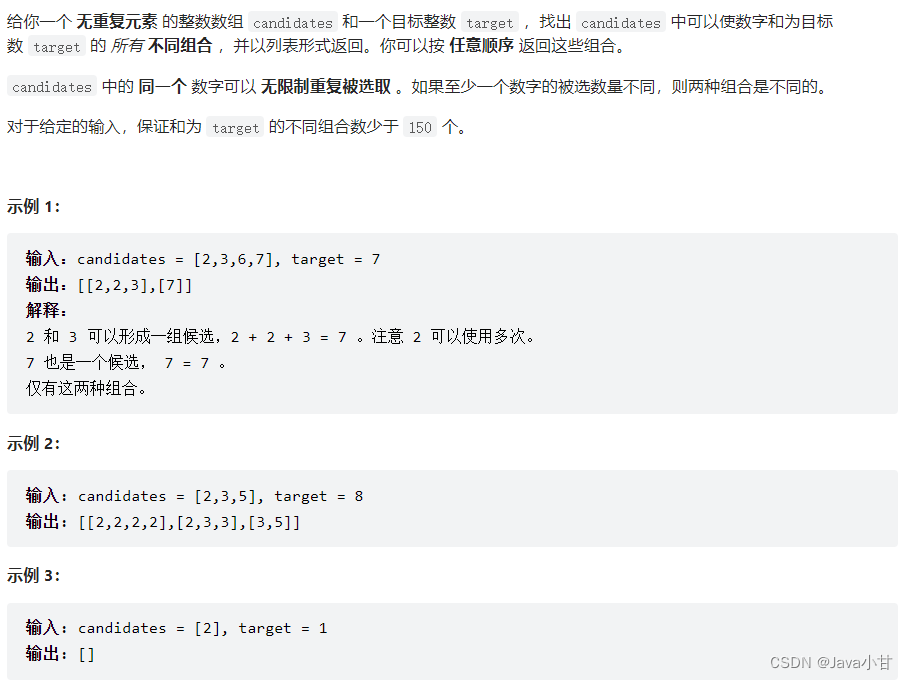
提示：

• 1 <= candidates.length <= 30
• 1 <= candidates[i] <= 200
• candidate 中的每个元素都 互不相同
• 1 <= target <= 500

这题跟上面那题思路基本差不多，有区别的是这题不需要剪枝操作，还有就是纵向遍历的时候，横向遍历的那个数还可以用的，这题数组是无序的，可以先进行排序，还有就是这题没有规定多少个元素和相加等于目标值。

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path= new LinkedList<>();
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);
       combinationSum1(candidates,target,0,0);
       return result;
    }
    public void combinationSum1(int[] candidates, int target,int startsum,int sum){
        if(sum>target) return;
        if(sum==target){
           result.add(new ArrayList<>(path));
           return;
        }

        for(int i=startsum;i<candidates.length;i++){
            //if(sum+candidates[i]>target) break;
             path.add(candidates[i]);
            sum+=candidates[i];
            combinationSum1(candidates,target,i,sum);
            sum-=candidates[i];
            path.removeLast();
        }
    }
}

六：组合总和Ⅱ

力扣40题目链接

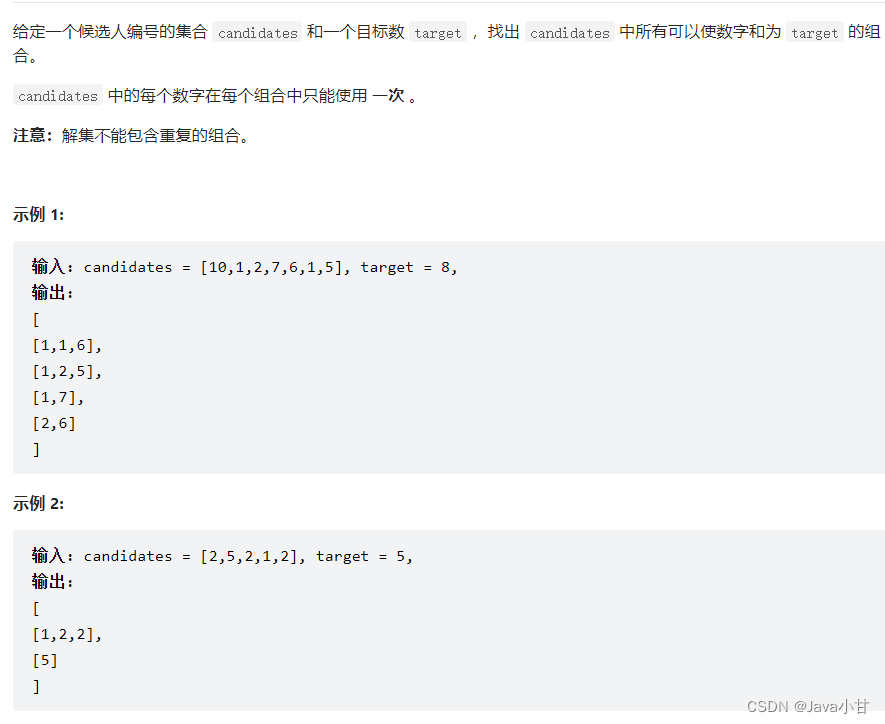
思路：大体思路和上面的几题差不多，这题的区别就是先排序，然后需要注意的就是两个相同的元素就没有必要继续遍历，可以进行剪枝操作比方说示例一中的数组，排序之后[1,1,2,5,6,7,10],也就是说横向遍历的时候索引1位置的数值因为和索引0位置的数值相等，就没有必要进行遍历，因为遍历出来的结果也是重复的，所以需要进行剪枝操作。

class Solution {
    List<List<Integer>> result=new ArrayList<>();
    LinkedList<Integer> path=new LinkedList<>();
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);
      combinationSum1(candidates,target,0,0);
      return result;
    }
    public void combinationSum1(int[] candidates, int target,int startsum,int sum){
        if(sum==target){
            result.add(new ArrayList(path));
            return;
        }


        for(int i=startsum;i<candidates.length;i++){
             if ( i>startsum&&candidates[i]==candidates[i-1]){
               continue;
            }//剪枝操作
         if(sum+candidates[i]>target) break;
            path.add(candidates[i]);
           sum+=candidates[i];
            combinationSum1(candidates,target,i+1,sum);
            sum-=candidates[i];//回溯
            path.removeLast();//回溯
        }
    }
}