LRU缓存算法
LRU思想:维护一个按时间从旧到新排序的链表结构,因为缓存大小有限,当缓存空间不足时,需要淘汰一个数据,此时直接删除头节点,时间复杂度O(1)。当要缓存数据时,需要先查找数据,如果没有查找到,则放到链表尾部,因为查找需要遍历链表时间复杂度是O(n),所以单纯用链表做LRU缓存算法的时间复杂度也是O(n),很高。
总结一下:
LRU算法需要三个功能:
1、往缓存空间添加数据
2、从缓存空间删除数据
3、从缓存空间查找数据
三个操作都涉及查找,所以单纯用链表的话,时间复杂度很高。但是散列表的查找时间复杂度是O(1),所以散列表+链表实现LRU的话,可以将三个功能操作的时间复杂度降到O(1)。
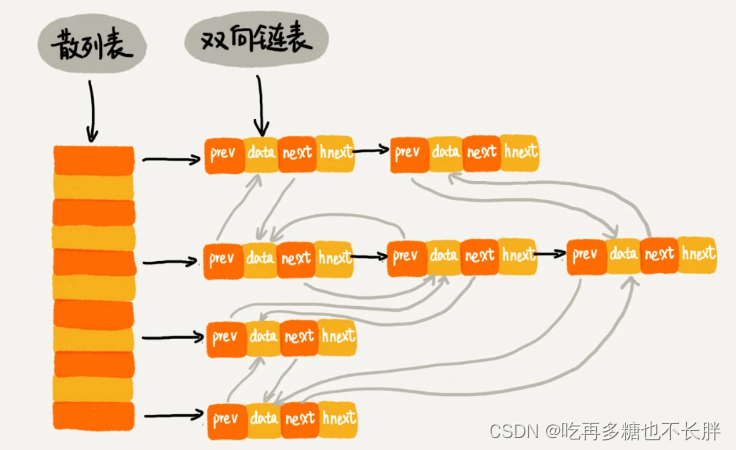
如图:
每个结点有
data:存储数据
prev:前驱指针,纵向指针,维护数据缓存的时间线
next:后继指针,纵向指针,维护数据缓存的时间线
hnext:横向指针,维护解决散列表的散列冲突的单链表。
next和hnext有什么区别呢,prev和next维护的是双向链表,按照时间缓存连接。
而hext维护的是散列表每个槽内的单链表。
散列表+链表实现LRU:
1、查找功能:散列表查找数据时间复杂度是O(1),查找到数据后,通过修改prev和next将数据移动到双向链表的尾部,但是hnext
2、删除功能:需要查找数据,然后删除。查找借助散列表查找数据,时间复杂度是O(1)。因为是双向链表,可以通过前驱指针和后继指针删除结点只要O(1)
3、添加功能:需要先看数据是否在缓存中,如果已经存在,需要移其道双向链表尾部;不存在的话,需要看缓存是否已满,满的话删除头部结点,然后把数据放到尾部,不满的话直接放到双向链表尾部。
总结:散列表+链表实现LRU,三个操作都是O(1),实现了一个高效的、支持LRU的缓存算法的存储系统原型。
有序集合
有序集合中有两个重要的属性,key键值和score分值,功能有:
1、添加成员对象
2、根据键值删除成员对象
3、根据键值查询成员对象
4、根据分值查找数据,例如查[100-356]的数据
5、根据分值从大到小排序数据。
如果只按照分值来将成员对象创建成跳表,那这样要实现删除、查找功能的时间复杂度是很高的。所以也是像LRU一样,根据key创建一个散列表,通过散列表实现查找、删除功能,时间复杂度是O(1),然后根据跳表实现对分值的排序以及查找。
JAVA LinkedHashMap
LinkedHashMap比HashMap多了一个linked,这并不是表示用linked链表解决散列冲突,而是表示双链表。实际上LinkedHashMap是通过双链表+散列表组合而成,原理与双链表+散列表的LRU缓存算法一致的。
例如:
HashMap<Integer, Integer> m = new LinkedHashMap<>();
m.put(3, 11);
m.put(1, 12);
m.put(5, 23);
m.put(2, 22);
for (Map.Entry e : m.entrySet()) {
System.out.println(e.getKey());
}
这段代码的输出顺序是3、1、5、2,正常散列表的数据是打乱后无规则存储的,但是这里是按插入顺序遍历打印的。实际上不仅可以按顺序遍历打印,还能按访问顺序遍历数据,与LRU一致。
// 10是初始大小,0.75是装载因子,true是表示按照访问时间排序
HashMap<Integer, Integer> m = new LinkedHashMap<>(10, 0.75f, true);
m.put(3, 11);
m.put(1, 12);
m.put(5, 23);
m.put(2, 22);
m.put(3, 26);
m.get(5);
for (Map.Entry e : m.entrySet()) {
System.out.println(e.getKey());
}
打印结果是1,2,3,5.
具体分析,4-7行代码后,数据添加到链表,链表呈现如下:
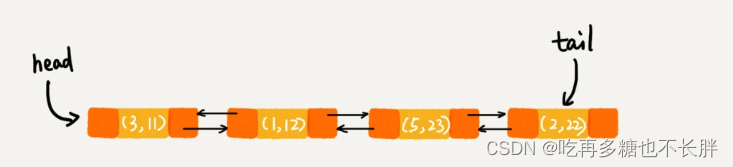
第9行代码后,将key=3的键值放入链表中,因为key=3在链表以及存在了,所以删除原来的(3,11),重新在链表尾部添加(3,26)
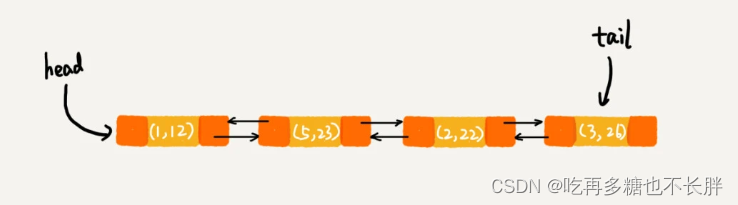
第10行代码后,查询key=9的数据,被查询的数据移动到尾部表示最新访问的。
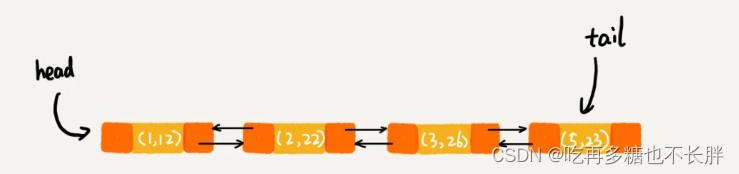
所以输出1,2,3,5
总结:LinkedHashMap与基于散列表+双向链表的LRU缓存算法原理一致,
为什么散列表总是跟链表一起使用
1、散列表的查找、插入、删除是很高效的,但是数据都是打乱无规律存储的,所以它无法支持按照某种顺序快速遍历数据。
2、链表或者跳表可以高效排序遍历列表的数据,所以二者需要结合使用。