文章目录
1.排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
排序默认排成升序
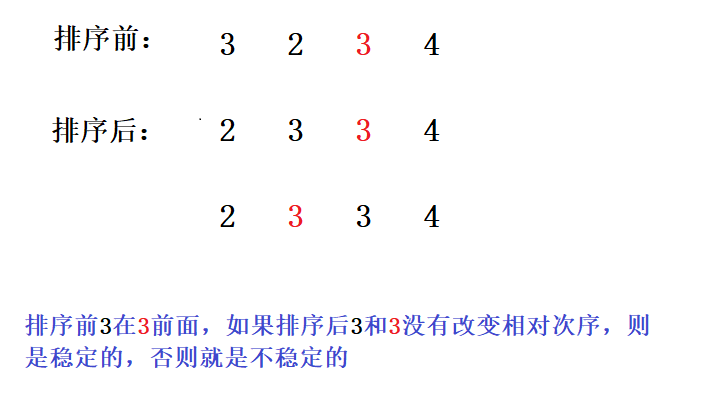
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持
不变,则称这种排序算法是稳定的;否则称为不稳定的。
一个本身就稳定的排序,可以实现为不稳定的排序。但是一个不稳定的排序不能实现成稳定的排序。
内部排序:数据元素全部放在内存中的排序
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-miYgXkqE-1665898381606)(…/AppData/Roaming/Typora/typora-user-images/image-20221014185911022.png)]
2.常见的排序算法
2.1 插入排序
2.1.1直接插入排序
插入排序是指在待排序的元素中,假设前面n-1(其中n>=2)个数已经是排好顺序的,现将第n个数插到前面已经排好的序列中,然后找到合适自己的位置,使得插入第n个数的这个序列也是排好顺序的。按照此法对所有元素进行插入,直到整个序列排为有序的过程,称为插入排序
思路:i从数组arr第二个元素开始遍历数组,把i下标的元素放到tmp中保存,j=i-1,比较arr[j]和tmp,如果arr[j]>tmp,arr[j+1]=arr[j],j–(保证j>=0),再比较arr[j]和tmp;如果arr[j]<tmp,arr[j+1]=tmp.
//1.直接插入排序
//适用于数据量不多,接近有序的情况
/**
* 时间复杂度:
* 最好情况下:(有序) O(n)
* 最坏情况下:(逆序) O(n^2)
* 空间复杂度:O(1)
* 稳定性:稳定
* @param array
*/
public static void insertSort(int[] array){
for (int i =1; i < array.length; i++) {
int tmp=array[i];
int j=i-1;
for (; j >=0; j--) {
if(array[j]>tmp){
array[j+1]=array[j];
}else{
//array[i]=tmp;
break;
}
}
array[j+1]=tmp;
}
}
不同情况下的排序耗时:
public static void testInsert(int[] array){
long start=System.currentTimeMillis();
Test1.insertSort(array);
long end=System.currentTimeMillis();
System.out.println("插入排序耗时: "+(end-start));
}
public static void inorder(int[] array){
for(int i=0;i< array.length;i++){
array[i]= i;
}
}
public static void main(String[] args) {
int[] array=new int[10_0000];
inorder(array);
testInsert(array);
}
//顺序情况下插入排序耗时: 3
public static void testInsert(int[] array){
long start=System.currentTimeMillis();
Test1.insertSort(array);
long end=System.currentTimeMillis();
System.out.println("插入排序耗时: "+(end-start));
}
public static void notInorder(int[] array){
Random random=new Random();
for(int i=0;i< array.length;i++){
array[i]=random.nextInt(10_0000);
}
}
public static void main(String[] args) {
int[] array=new int[10_0000];
notInorder(array);
testInsert(array);
}
//乱序情况下插入排序耗时: 701
public static void testInsert(int[] array){
long start=System.currentTimeMillis();
Test1.insertSort(array);
long end=System.currentTimeMillis();
System.out.println("插入排序耗时: "+(end-start));
}
public static void reverseInorder(int[] array){
for(int i=0;i< array.length;i++){
array[i]= array.length-i;
}
}
public static void main(String[] args) {
int[] array=new int[10_0000];
//inorder(array);
notInorder(array);
//reverseInorder(array);
testInsert(array);
}
//逆序情况下插入排序耗时: 1312
2.1.2希尔排序
希尔排序是通过分组+插入
希尔排序是插入排序的一种又称“缩小增量排序”,是直接插入排序算法的一种更高效的改进版本。希尔排序是
非稳定排序算法。希尔排序是把记录按下标的一定增量分组,对每组使用
直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至 1 时,整个文件恰被分成一组,算法便终止。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wu2jD9V1-1665898381607)(…/AppData/Roaming/Typora/typora-user-images/image-20221014212123568.png)]
图中相同颜色的为一组,每一组内进行插入排序
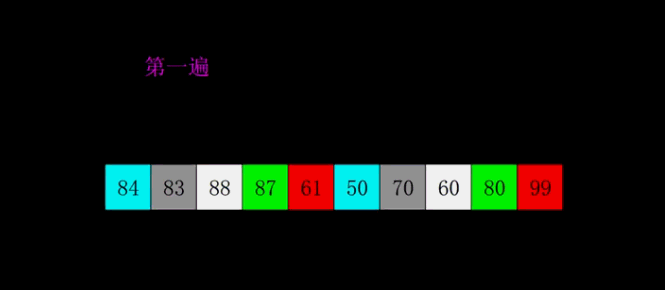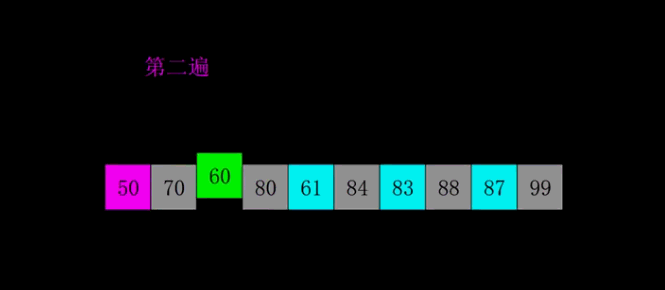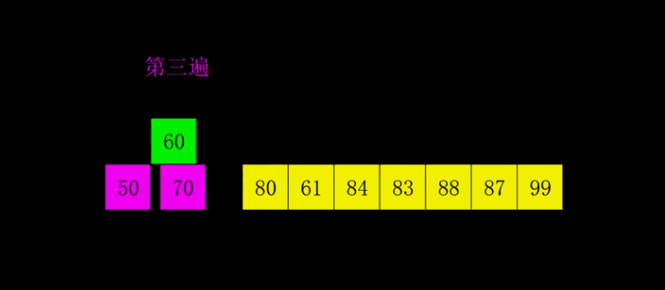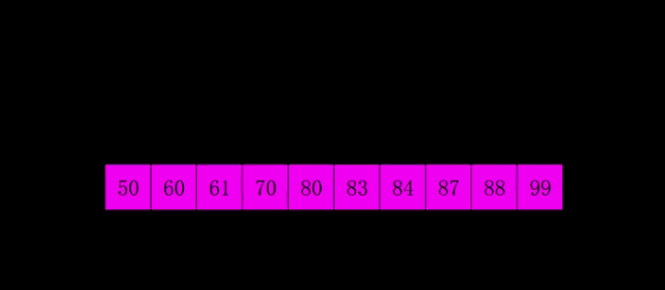
希尔排序的时间的时间复杂度为O(n^1.3)
public static void shell(int[] array,int gap){
for (int i =gap; i < array.length; i++) {
int tmp=array[i];
int j=i-gap;
for (; j >=0; j-=gap) {
if(array[j]>tmp){
array[j+gap]=array[j];
}else{
//array[i]=tmp;
break;
}
}
array[j+gap]=tmp;
}
}
public static void shellSort(int[] array){
int gap= array.length;
while(gap>1){
gap/=2;
shell(array,gap);
}
2.2 选择排序
2.2.1直接选择排序
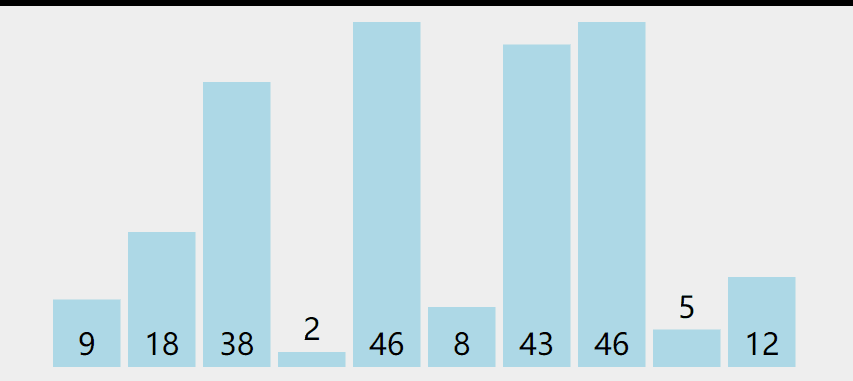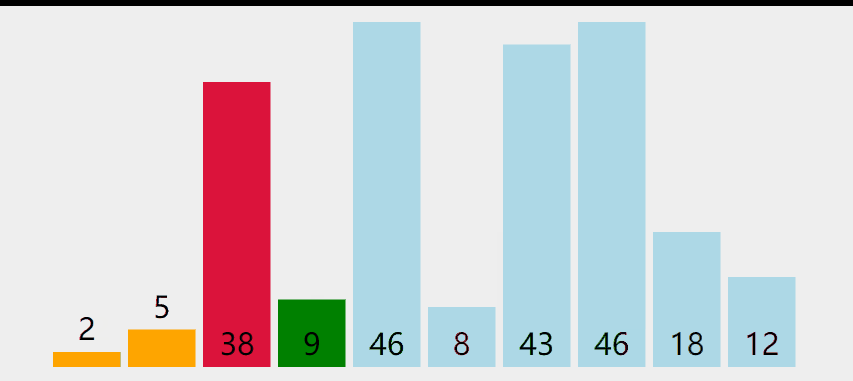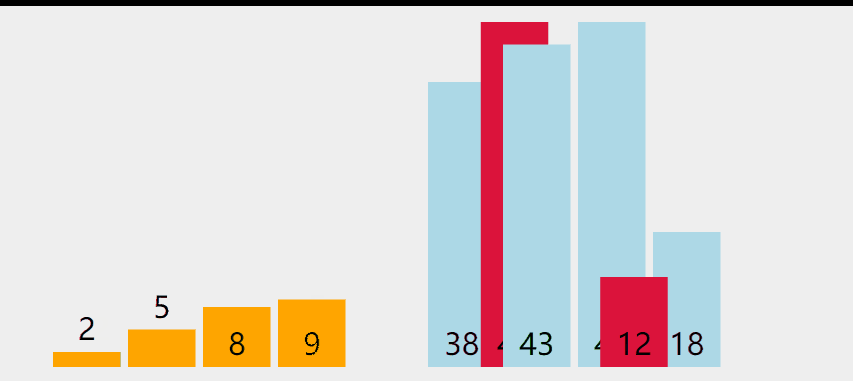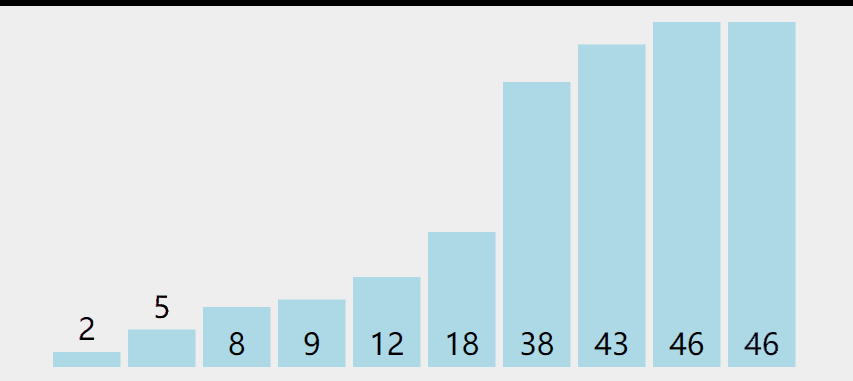
工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。
public static void selectSort(int[] array){
for(int i=0;i<array.length;i++){
int minIndex=i;
for (int j = i+1; j < array.length; j++) {
if(array[i]>array[j]){
//更新minIndex的值
minIndex=j;
}
}
//处理两个下标相同的情况
if(i!=minIndex){
swap(array,i,minIndex);
}
}
}
时间复杂度:O(n^2)
空间复杂度:O(1)
稳定性:不稳定
另一种思路:从头和尾同时向中间找最大值和最小值下标,最大值放到后面,最小值放到前面,直到找到最中间的元素为止
//时间复杂度:O(n^2)
public static void selectSort2(int[] array){
int left=0;
int right=array.length-1;
while(left<right){
int i=left;
int minIndex=i;
int maxIndex=i;
while(i<=right){
if(array[i]<array[minIndex]){
minIndex=i;
}
if(array[i]>array[maxIndex]){
maxIndex=i;
}
i++;
}
//把最小值放到前面
swap(array,minIndex,left);
//如果left==maxIndex,说明上面已经把最大值换到了minIndex位置
if(left==maxIndex){
maxIndex=minIndex;
}
//把最大值放到后面
swap(array,maxIndex,right);
left++;
right--;
}
}
2.2.2堆排序
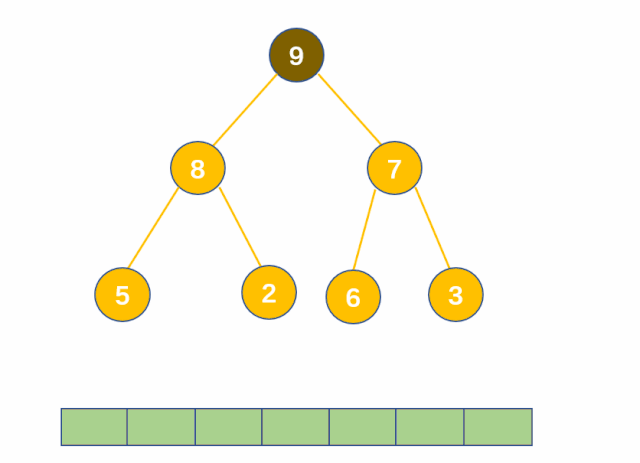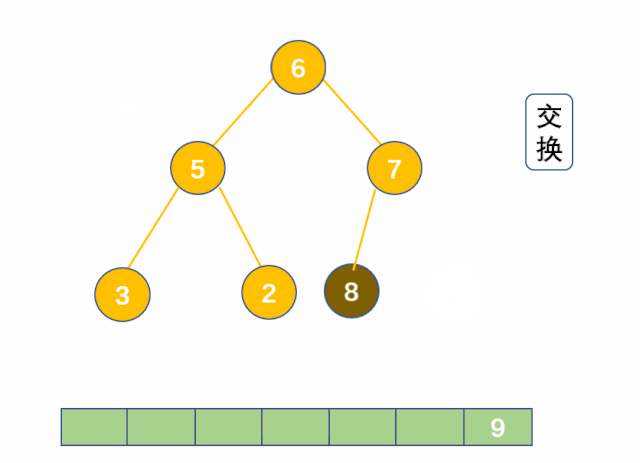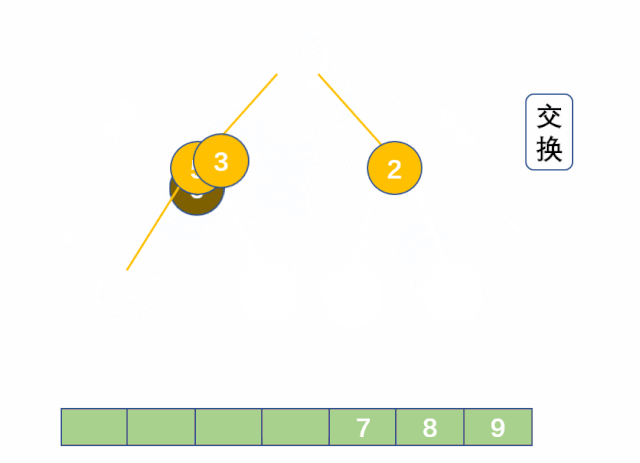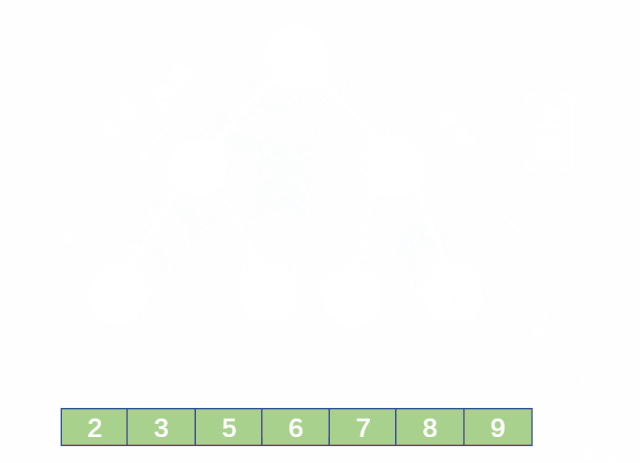
堆排序是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。
public static void swap(int[] array,int i,int j){
int tmp=array[i];
array[i]=array[j];
array[j]=tmp;
}
private static void createBigHeap(int[] array){
for(int parent= (array.length-1-1)/2;parent>=0;parent--){
shiftDown(array,parent,array.length);
}
}
private static void shiftDown(int[] array,int parent,int len){
int child=parent*2+1;
while(child<len){
if(child+1<len&&array[child]<array[child+1]){
child++;
}
if(array[child]>array[parent]){
swap(array,child,parent);
parent=child;
child=parent*2+1;
}else{
break;
}
}
}
//时间复杂度:O(n+nlogn)约等于O(nlogn)
//空间复杂度:O(1)
//不稳定
public static void heapSort(int[] array){
createBigHeap(array);//O(n)
for(int i= array.length-1;i>0;i--){
swap(array,0,i);
shiftDown(array,0,i);//O(logn)
}
//
}
2.3交换排序
2.3.1冒泡排序
//时间复杂度:(不考虑优化) O(n^2)
//空间复杂度:O(1)
//稳定
public static void bubbleSort(int[] array){
//最外面的控制趟数
for(int i=0;i<array.length-1;i++){
boolean flg=false;
for (int j = 0; j < array.length-1-i; j++) {
if(array[j]>array[j+1]){
swap(array,j,j+1);
flg=true;
}
}
if(!flg){
break;
}
}
}
2.3.2快速排序
基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程(递归),直到所有元素都排列在相应位置上为止。(分治思想)
- Hoare版
//时间复杂度:O(nlogn)
// 有序情况下:O(n^2)
//空间复杂度:O(logn)
// 有序情况下:O(n)
//不稳定
public static void quickSort(int[] array){
quick(array,0,array.length-1);
}
public static void quick(int[] array,int start,int end){
//不能写“=”,防止1,2,3,4这种没有左数或右数的情况。
if(start>=end){
return;
}
int pivot=partitionHoare(array,start,end);
quick(array,start,pivot-1);
quick(array,pivot+1,end);
}
public static int partitionHoare(int[] array,int left,int right){
int i=left;
int pivot=array[left];
while(left<right){
//1.为什么right先走?
//2.为什么是”>=“?
while(left<right&&array[right]>=pivot){
//left<right防止后面都比基准大
right--;
}
while(left<right&&array[left]<=pivot){
left++;
}
swap(array,left,right);
}
swap(array,i,left);
return left;
}
1.如果left先走,eg:
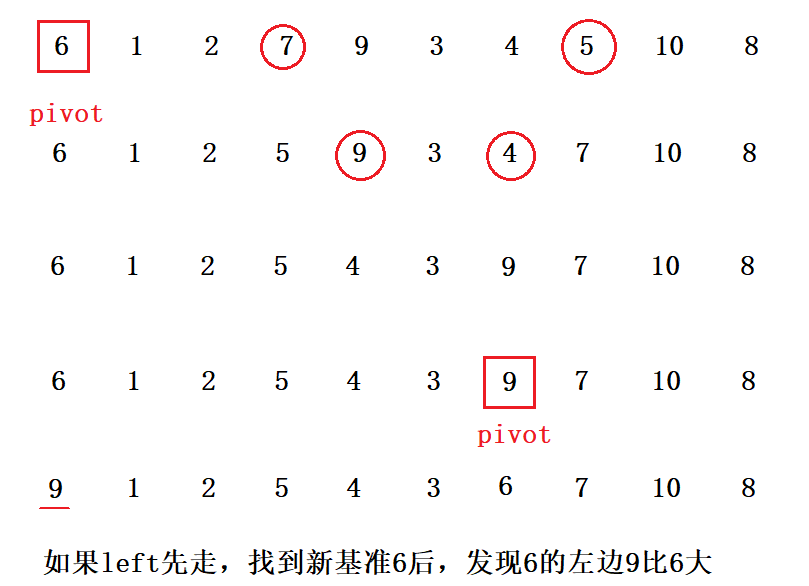
2.为什么是”>=“?

2.挖坑法
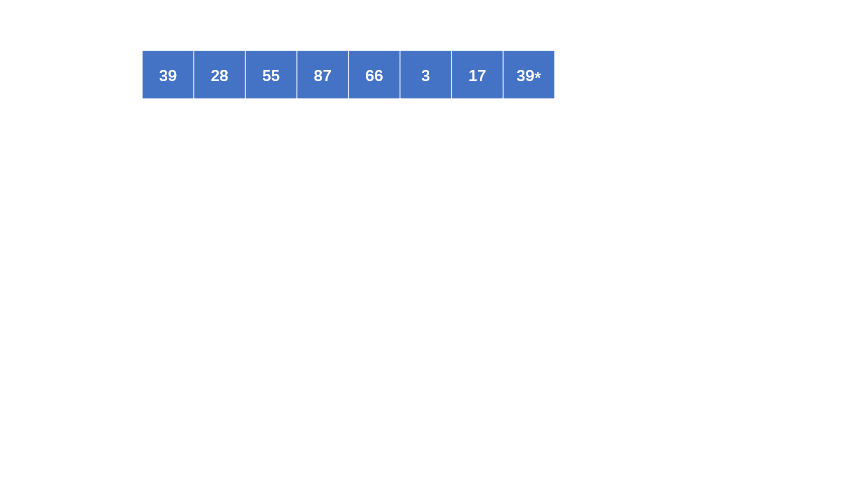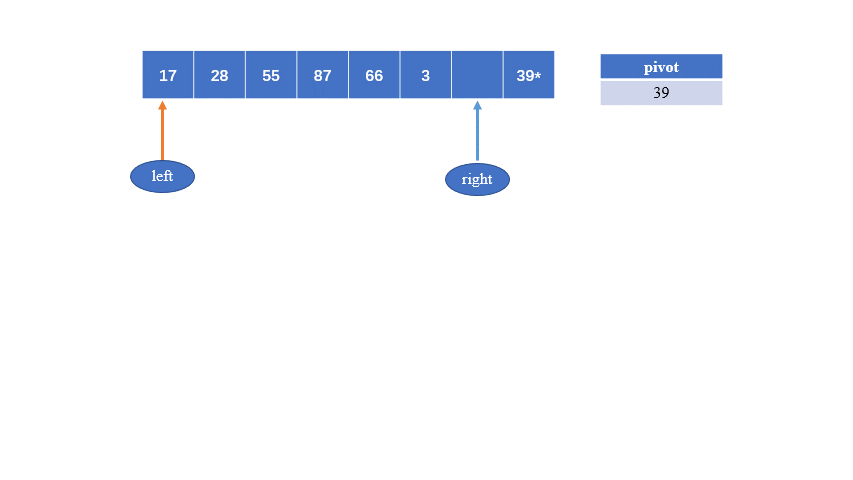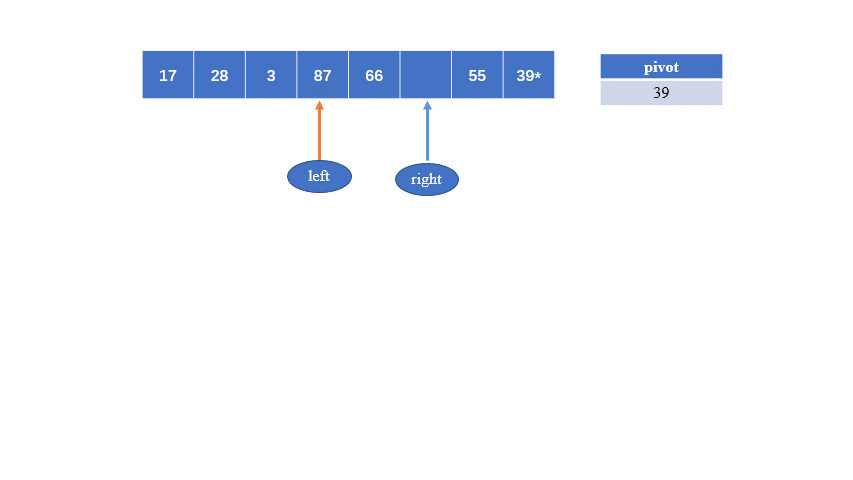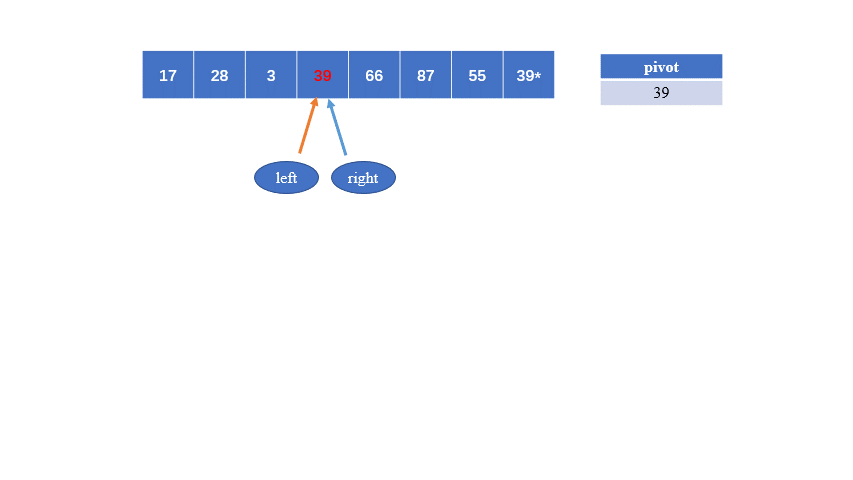
public static int partition(int[] array,int left,int right){
int pivot=array[left];
while(left<right){
while(left<right&&array[right]>=pivot){
right--;
}
array[left]=array[right];
while(left<right&&array[left]<=pivot){
left++;
}
array[right]=array[left];
}
array[left]=pivot;
return left;
}
做题一般优先用挖坑法
3.前后指针法
public static int partition1(int[] array,int left,int right){
int prev=left;
int cur=prev+1;
while(cur<=right){
if(array[cur]<array[left]&&array[++prev]!=array[cur]){
swap(array,prev,cur);
}
cur++;
}
swap(array,prev,left);
return prev;
}
总结:这三种方法找到的基准左右两边的序列可能不一样。
快速排序优化
-
三数取中法选key
-
递归到小的子区间时,可以考虑使用插入排序
public static void quick(int[] array,int start,int end){ if(start>=end){ return; } if(end-start+1<=15){ //递归越深后面几层越来越趋于有序,使用插入排序 //小区间用插入排序 insertSort(array,start,end); return; } //在使用partition找基准之前,尽量能去解决划分不均匀的问题,没有左树或没有右树 //三数取中法 int index=findMidValOfIndex(array,start,end); swap(array,start,index); int pivot=partition1(array,start,end); quick(array,start,pivot-1); quick(array,pivot+1,end); } public static int findMidValOfIndex(int[] array,int start,int end){ int mid=(end+start)/2; if(array[start]<array[end]){ if(array[mid]<array[start]){ return start; }else if(array[mid]>array[end]){ return end; }else{ return mid; } }else{ if(array[mid]<array[end]){ return end; }else if(array[mid]>array[start]){ return start; }else{ return mid; } } }快速排序非递归
public static void quickSort1(int[] array){ Stack<Integer> stack=new Stack<>(); int start=0; int end=array.length-1; int pivot=partition1(array,start,end); //判断左边有2个元素 if(start<pivot-1){ stack.push(start); stack.push(pivot-1); } //判断右边有2个元素 if(end>pivot+1){ stack.push(pivot+1); stack.push(end); } while(!stack.isEmpty()){ end=stack.pop(); start=stack.pop(); pivot=partition1(array,start,end); if(start<pivot-1){ stack.push(start); stack.push(pivot-1); } if(end>pivot+1){ stack.push(pivot+1); stack.push(end); } } }
2.4归并排序
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
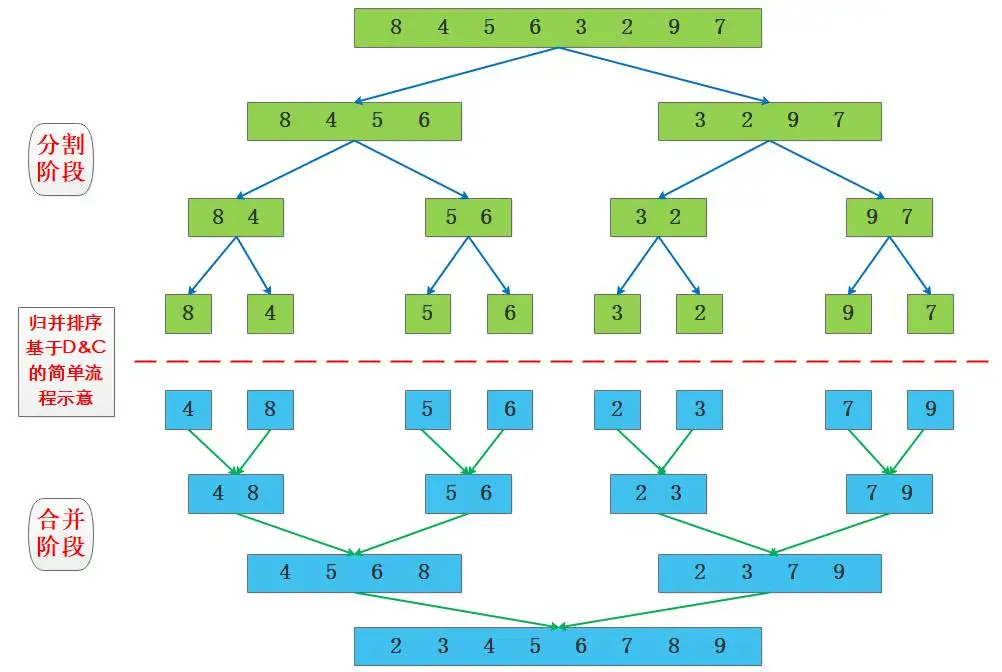
public static void mergeSort(int[] array){
mergeSortChild(array,0,array.length-1);
}
public static void mergeSortChild(int[] array,int left,int right){
if(left==right){
return;
}
int mid=(left+right)/2;
mergeSortChild(array,left,mid);
mergeSortChild(array,mid+1,right);
merge(array,left,right,mid);
}
public static void merge(int[] array,int left,int right,int mid){
int len=right-left+1;
int[] tmp=new int[len];
int i=0;
int s1=left;
int e1=mid;
int s2=mid+1;
int e2=right;
while(s1<=e1&&s2<=e2){
if(array[s1]<=array[s2]){
tmp[i++]=array[s1++];
}else{
tmp[i++]=array[s2++];
}
}
while(s1<=e1){
tmp[i++]=array[s1++];
}
while(s2<=e2){
tmp[i++]=array[s2++];
}
//tmp当前的数据是left和right之间有序的数据,覆盖数组中原来的数据
for(int k=0;k<len;k++){
array[k+left]=tmp[k];
}
}
//时间复杂度:O(N*logN) 主要是归并过程
//空间复杂度:O(N)
//稳定性:稳定
归并排序非递归
public static void mergeSort1(int[] array){
for(int gap=1;gap<array.length;gap*=2){
for(int i=0;i<array.length;i+=gap*2){
int left=i;
int mid=left+gap-1;
if(mid>=array.length){
mid=array.length-1;
}
int right=mid+gap;
if(right>=array.length){
right=array.length-1;
}
merge(array,left,right,mid);
}
}
}
3.排序算法总结
| 排序方法 | 时间复杂度(平均) | 时间复杂度(最坏) | 时间复杂度(最好) | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 插入 | 稳定 | ||||
| 希尔 | 不稳定 | ||||
| 选择 | 不稳定 | ||||
| 堆 | 不稳定 | ||||
| 冒泡 | 稳定 | ||||
| 快速 | 不稳定 | ||||
| 归并 | 稳定 |
4.其他非基于比较排序
计数排序
思想:计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤:
? 1、取无序数组arr中的最大值max和最小值min,新建(max-min +1)长度的数组tmp。
? 2、遍历无序数组,取其中元素-min作为新建数组的索引,存在一个则新数组该索引所在的值自增。
? 3、遍历新数组,当存在不为0的元素,取该元素的索引+min放入最终数组,并且该元素自减,直到为0,返回最终数组。
它的优势在于在对一定范围内的整数排序时,它的复杂度为Ο(n+k)(其中k是整数的范围),快于任何比较排序算法。当然这是一种牺牲空间换取时间的做法,而且当O(k)>O(nlog(n))的时候其效率反而不如基于比较的排序(基于比较的排序的时间复杂度在理论上的下限是O(nlog(n)), 如归并排序,堆排序)
/*计数排序:范围小 且集中的数据
时间复杂度:O(n+范围) 范围越小,时间复杂度越小
空间复杂度:O(范围)*/
public static void countSort(int[] array){
//找最大值找最小值,确定计数数组大小
int min=array[0];
int max=array[0];
for(int i=0;i<array.length;i++){
if(array[i]<min){
min=array[i];
}
if(array[i]>max){
max=array[i];
}
}
int len=max-min+1;
int[] tmp=new int[len];
//开始遍历 当前数组 统计每个数字出现的次数 O(n)
for(int i=0;i<array.length;i++){
int val=array[i];
tmp[val-min]++;
}
int k=0;
//遍历计数数组,看每个下标的值是几,就打印几个下标的数据 O(范围 + n)
for(int i=0;i<tmp.length;i++){
while(tmp[i]>0){
array[k++]=i+min;
tmp[i]--;
}
}
}