[数据结构与算法]数据结构与算法之线性表

1. 顺序表

1.1 概念

• 线性表是最常见最基本、最简单的数据结构。一个线性表是n个具有相同特性的数据元素的有限序列。
• 前驱元素：若A元素在B元素前面，则称A为B的前驱元素。
• 后继元素：若B元素在A元素后面，则称B为A的后继元素。
• 线性表的特征：数据元素之间具有一种“一对一”的逻辑关系。
• 第一个数据元素没有前驱，这个数据元素被称为头结点。
• 最后一个元素没有后继，这个元素被称为尾结点。
• 除了第一个和最后一个元素之外，其他的元素有且仅有一个前驱和一个后继。
  
• 线性表的分类：线性表中存储数据可以是顺序存储，也可以是链式存储，按照数据的存储方式不同，可以把线性表分为顺序表和链表。

1.2 顺序表

• 顺序表是在计算机内存中以数组的形式保存的线性表，线性表的顺序存储是指用一组连续的存储单元，依次存储线性表中的各个元素，使得线性表中在逻辑上相邻的数据元素在相邻的物理存储单元中，即通过数据元素物理存储的相邻关系来反映数据元素之间逻辑上的相邻关系。
• 顺序表的API设计：
  
• 顺序表的代码实现：

package com.tiger.study.DataStructure.Linear;

public class SequenceList<T>{
    // 存储元素的数组
    private T[] eles;

    // 记录当前顺序表中的元素个数
    private int N;

    // 构造方法
    public SequenceList(int capacity) {
        // 初始化数组
        this.eles = (T[]) new Object[capacity];

        // 初始化长度
        this.N = 0;
    }

    // 将一个线性表置为空
    public void clear() {
        this.N = 0;
    }

    // 判断当前线性表是否为空表
    public boolean isEmpty() {
        return N == 0;
    }

    // 获取线性表的长度
    public int length() {
        return N;
    }

    // 获取指定位置的元素
    public T get(int i) {
        return eles[i];
    }

    // 向线性表中添加元素
    public void insert(T t) {
        if (N == eles.length) {
            resize(eles.length * 2);
        }
        eles[N++] = t;
    }

    // 在i元素处插入元素t
    public void insert(int i, T t) {
        if (N == eles.length) {
            resize(eles.length * 2);
        }
        // 先把i索引处的元素及其后面的元素向后移动一位
        for (int index = N; index > i; index--) {
            eles[index] = eles[index - 1];
        }
        // 再把t元素放到i索引处即可
        eles[i] = t;
        N++;
    }

    // 删除指定位置i处的元素，并返回该元素
    public T remove(int i) {
        // 记录索引i处的值
        T current = eles[i];

        // 索引i后面元素依次向前移动一位即可
        for (int index=i; index < N - 1; index++) {
            eles[index] = eles[index+1];
        }
        N--;

        if (N >0 && N < eles.length / 4) {
            resize(eles.length/2);
        }
        return current;
    }

    // 查找t元素第一次出现的位置
    public int indexOf(T t) {
        for (int i = 0; i < N; i++) {
            if (eles[i].equals(t)) {
                return i;
            }
        }
        return -1;
    }

    public void resize(int newSize) {
        // 记录旧数组
        T[] temp = eles;

        // 创建新数组
        eles = (T[]) new Object[newSize];

        // 把旧数组中的元素拷贝到新数组
        for (int i = 0; i < N; i++) {
            eles[i] = temp[i];
        }
    }

}

1.2 链表

• 链表是一种物理存储单元上非连续、非顺序的存储结构。链表中的数据元素的逻辑顺序是通过链表中的指针依次链接实现的。链表由一系列结点（链表中每个元素称为结点）组成，结点可以在运行时动态生成。
  

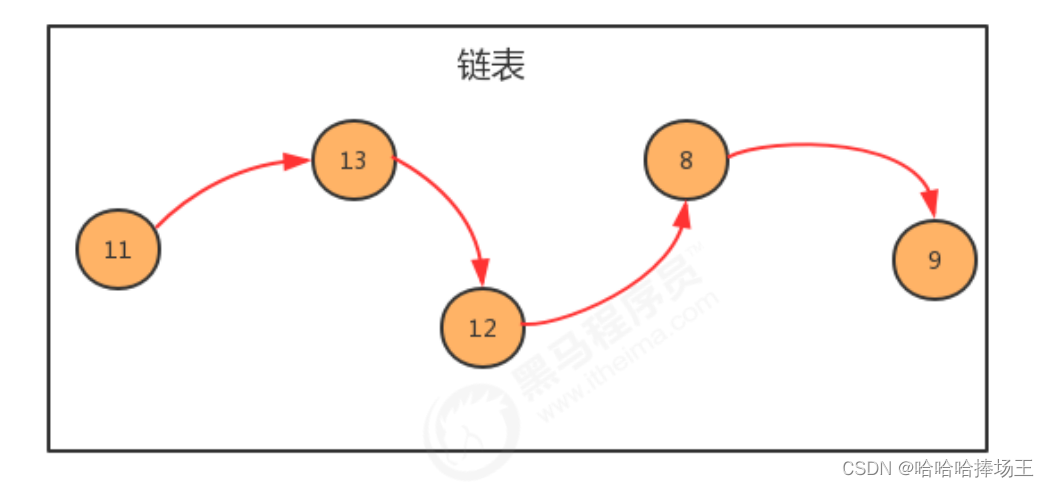
1.2.1 单项链表

• 单项链表是链表的一种，它由多个结点组成，每个结点都由一个数据域和一个指针域组成，数据域用来存储数据，指针域用来指向其后继结点。链表的头节点的数据域不存储数据，指针域指向第一个存储数据的结点。
  
• 单链表的API设计
  
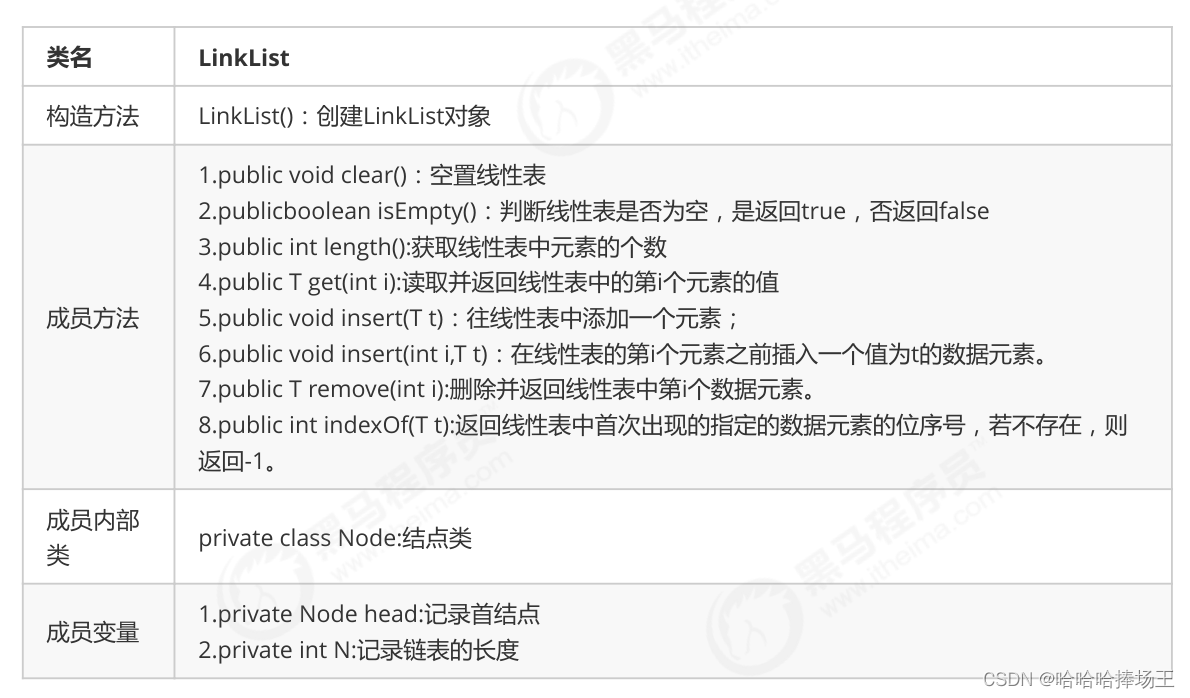• 单链表代码实现

package com.tiger.study.DataStructure.Linear;

import java.util.Iterator;

public class LinkList<T> implements Iterable<T>{
    // 记录头节点
    private Node head;

    // 链表长度
    private int N;

    private class Node {
        // 存储数据
        T item;

        // 下一个节点
        Node next;

        public Node(T item, Node next) {
            this.item = item;
            this.next = next;
        }

    }

    public LinkList() {
        // 初始化头节点
        this.head = new Node(null, null);

        // 初始化元素个数
        this.N = 0;
    }

    // 清空链表
    public void clear() {
        head.next = null;

        // 初始化元素个数
        this.N = 0;
    }

    // 获取链表的长度
    public int length() {
        return N;
    }

    // 判断链表是否为空
    public boolean isEmpty() {
        return N == 0;
    }

    // 获得指定为i处的元素
    public T get(int i) {
        // 通过循环依次往后找
        Node n = head.next;
        for (int index = 0; index < i; index++) {
            n = n.next;
        }
        return n.item;
    }

    // 向链表中添加元素t
    public void insert(T t) {
        // 找到当前最后一个节点
        Node n = head;
        while (n.next != null) {
            n = n.next;
        }
        // 创建新节点，保存元素t,让当前最后一个节点指向新节点
        n.next = new Node(t, null);

        // 元素的个数+1
        N++;
    }

    // 向指定位置i处添加元素t
    public void insert(int i, T t) {
        // 找到i位置前一个结点
        Node pre = head;
        for (int index = 0; index < i; index++) {
            pre = pre.next;
        }

        // 找到i位置的结点
        Node curr = pre.next;

        // 创建新节点，并且新节点需要指向原来i位置的结点
        Node newNode = new Node(t, curr);

        // 原来i位置的前一个节点指向新结点即可
        pre.next = newNode;

        // 元素的个数+1
        N++;
    }

    // 删除指定位置i处的元素，并返回被删除的元素
    public T remove(int i) {
        // 找到i位置的前一个结点
        Node pre = head;
        for (int index = 0; index < i; index++) {
            pre = pre.next;
        }

        // 找到i位置的结点
        Node curr = pre.next;

        // 找到i位置的下一个结点
        Node nextNode = curr.next;

        // 前一个结点指向下一个结点
        pre.next = nextNode;

        // 元素个数-1
        N--;

        return curr.item;
    }

    // 查找元素t在链表中第一次出现的位置
    public int indexOf(T t) {
        Node n = head;
        for (int i = 0; n.next != null; i++) {
            n = n.next;
            if (n.item.equals(t)) {
                return i;
            }
        }
        return -1;
    }

    // 用来反转整个链表
    public void reverse() {
        // 判断当前列表是否为空列表，如果是空列表则结束运行，如果不是则调用重载的reverse方法
        if (isEmpty()) {
            return;
        }
        reverse(head.next);
    }

    // 用来反转指定元素
    public Node reverse(Node curr) {
        if (curr.next == null) {
            head.next = curr;
            return curr;
        }
        // 递归的反转当前结点curr的下一个结点；返回值就是链表反转后，当前结点的上一个结点
        Node pre = reverse(curr.next);
        // 让返回结点的下一个结点变为curr
        pre.next = curr;
        // 把当前结点的下一个结点变为null
        curr.next = null;
        return curr;
    }

    @Override
    public Iterator<T> iterator() {
        return new LIterator();
    }

    private class LIterator implements Iterator{
        private Node n;

        public LIterator() {
            this.n = head;
        }

        @Override
        public boolean hasNext() {
            return n.next != null;
        }

        @Override
        public Object next() {
            n = n.next;
            return n.item;
        }
    }
}

1.2.2 双向链表

• 双向链表也叫双向表，是链表的一种，它由多个结点组成，每个结点都由一个数据域和两个指针域组成，数据域用来存储数据，其中一个指针域用来指向后继结点，另一个指针域用来指向前驱结点。链表的头节点的数据域不存储数据，指向前驱结点的指针域值为null，指向后继节点的指针域指向第一个真正存储数据的结点。
  
• 双向链表的API设计
  
  
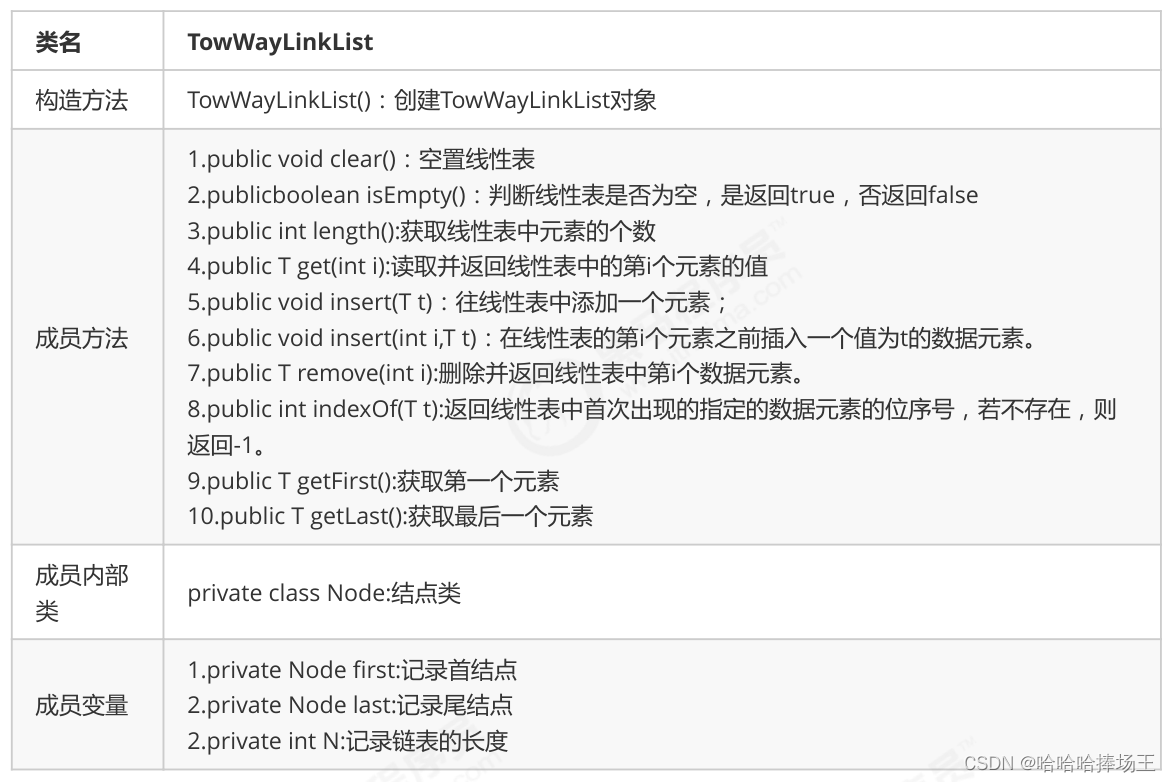• 双向链表的代码实现：

package com.tiger.study.DataStructure.Linear;

import java.util.Iterator;

public class TwoWayLinkList<T> implements Iterable<T> {
    // 首结点
    private Node head;

    // 最后一个结点
    private Node last;

    // 链表的长度
    private int N;

    private class Node {
        // 存储数据
        public T item;

        // 指向上一个结点
        public Node pre;

        // 指向下一个结点
        public Node next;

        public Node(T item, Node pre, Node next) {
            this.item = item;
            this.pre = pre;
            this.next = next;
        }
    }

    public TwoWayLinkList() {
        // 初始化头节点和尾结点
        this.head = new Node(null, null, null);
        this.last = null;

        // 初始化长度
        this.N = 0;
    }

    // 清空链表
    public void clear() {
        this.head.next = null;
        this.head.pre = null;
        this.head.item = null;
        this.last = null;
        this.N = 0;
    }

    // 获取链表长度
    public int length() {
        return N;
    }

    // 判断链表是否为空
    public boolean isEmpty() {
        return N == 0;
    }

    // 获取第一个元素
    public T getFirst() {
        if (isEmpty()) {
            return null;
        }
        return head.next.item;
    }

    // 获取最后一个元素
    public T getLast() {
        if (isEmpty()) {
            return null;
        }
        return last.item;
    }

    // 插入元素
    public void insert(T t) {
        // 如果链表为空
        if (isEmpty()) {
            // 创建新的结点
            Node node = new Node(t, head, null);
            // 让新结点成为尾结点，让头结点指向尾结点
            last = node;
            head.next = last;
        } else {
            Node oldLast = last;
            // 创建新的结点
            Node node = new Node(t, oldLast, null);

            // 让当前的尾结点指向新结点，让新结点成为尾结点
            oldLast.next = node;
            last = node;
        }

        // 元素+1
        N++;
    }

    // 向指定位置i处插入元素t
    public void insert(int i, T t) {
        // 找到i位置的前一个结点
        Node pre = head;
        for (int j = 0; j < i; j++) {
            pre = pre.next;
        }

        // i位置的结点
        Node curr = pre.next;

        // 创建新结点
        Node node = new Node(t, pre, curr);

        // 让i位置的前一个结点的下一个结点变为新结点
        pre.next = node;
        // 让i位置的前一个结点变为新结点
        curr.pre = node;

        N++;
    }

    // 获取指定位置i处的元素
    public T get(int i) {
        Node n = head.next;
        for (int j = 0; j < i; j++) {
            n = n.next;
        }
        return n.item;
    }

    // 找到元素t在链表中第一次出现的位置
    public int indexOf(T t) {
        Node n = head;
        for (int i = 0; n.next != null; i++) {
            n = n.next;
            if (n.next.equals(t)) {
                return i;
            }
        }
        return -1;
    }

    // 删除i位置的结点
    public T remove(int i) {
        // 找到i位置的前一个结点
        Node pre = head;
        for (int j = 0; j < i; j++) {
            pre = pre.next;
        }

        // 找到i位置的结点
        Node cur = pre.next;

        // 让i位置的前一个结点的下一个结点变为i位置的下一个结点
        pre.next = cur.next;

        // 让i位置的下一个结点的下一个结点的前一个结点变为i位置的前一个结点
        cur.next.pre = pre;
        N--;

        return cur.item;
    }


    @Override
    public Iterator<T> iterator() {
        return new TIterator();
    }

    private class TIterator implements Iterator {
        private Node n;

        public TIterator() {
            this.n = head;
        }

        @Override
        public boolean hasNext() {
            return n.next != null;
        }

        @Override
        public Object next() {
            n = n.next;
            return n.item;
        }
    }
}

1.2.4 链表的反转

• 需求：将一个链表反转
  
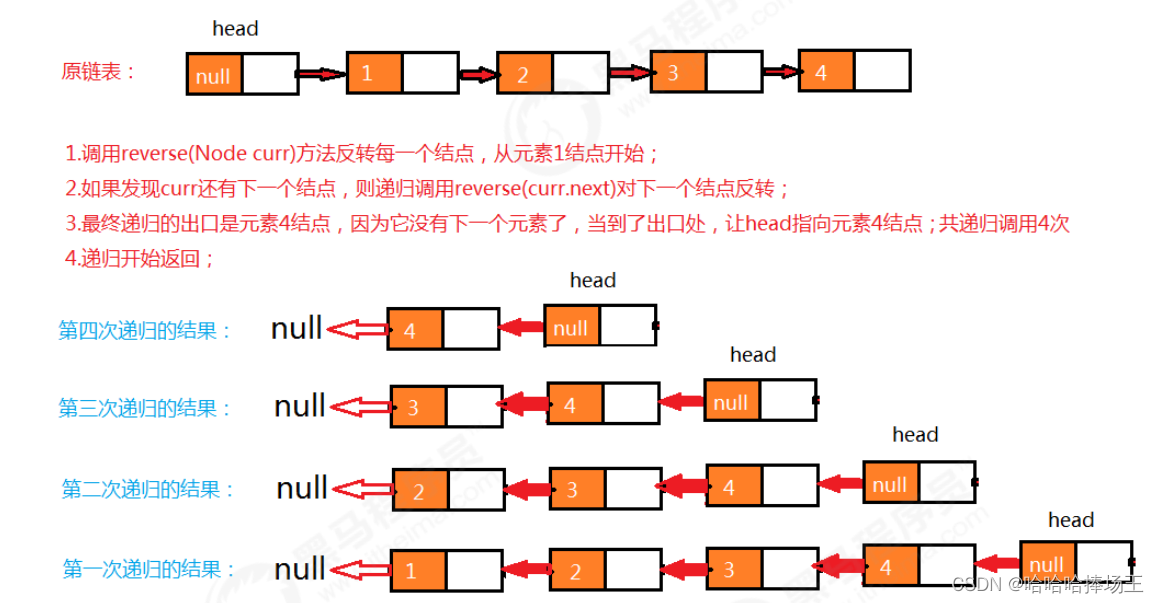• 代码实现：见链表的实现

1.2.5 快慢指针

• 快慢指针就是定义两个指针，这两个指针的移动速度一快一慢，以此来制造出自己想要的插值，这个差值可以帮我们找到链表上相应的结点。
• 中间值问题：找到链表的中间值
  

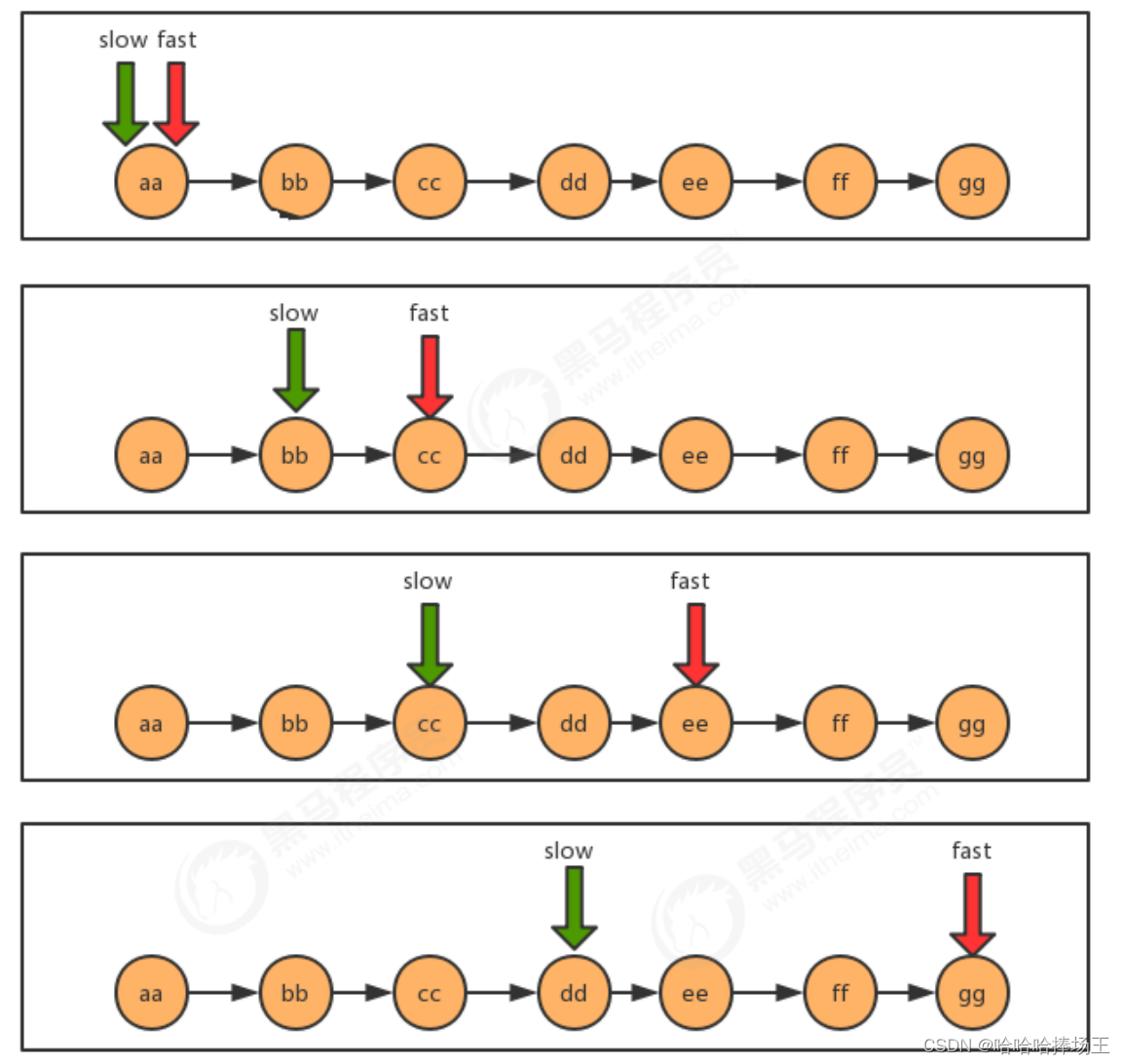
package com.tiger.study.DataStructure.Test;

// 快慢指针解决中间值问题

import com.tiger.study.DataStructure.Linear.LinkListNode;

public class FastSlowTestMid {

    public static void main(String[] args) {
        Node<String> first = new Node<String>("aa", null);
        Node<String> second = new Node<String>("bb", null);
        Node<String> third = new Node<String>("cc", null);
        Node<String> fourth = new Node<String>("dd", null);
        Node<String> fifth = new Node<String>("ee", null);
        Node<String> six = new Node<String>("ff", null);
        Node<String> seven = new Node<String>("gg", null);

        first.next = second;
        second.next = third;
        third.next = fourth;
        fourth.next = fifth;
        fifth.next = six;
        six.next = seven;

        System.out.println("中间值为：" + getMid(first));
    }

    // 得到中间值
    public static String getMid(Node<String> first) {
        Node<String> fast = first;
        Node<String> slow = first;

        while (fast.next != null && fast != null) {
            fast = fast.next.next;
            slow = slow.next;
        }

        return slow.item;
    }

    // 结点类
    private static class Node<T> {
        // 存储元素
        public T item;

        // 指向下一个结点
        public Node next;

        public Node(T item, Node next) {
            this.item = item;
            this.next = next;
        }
    }


}

• 单向链表是否有环问题：
  

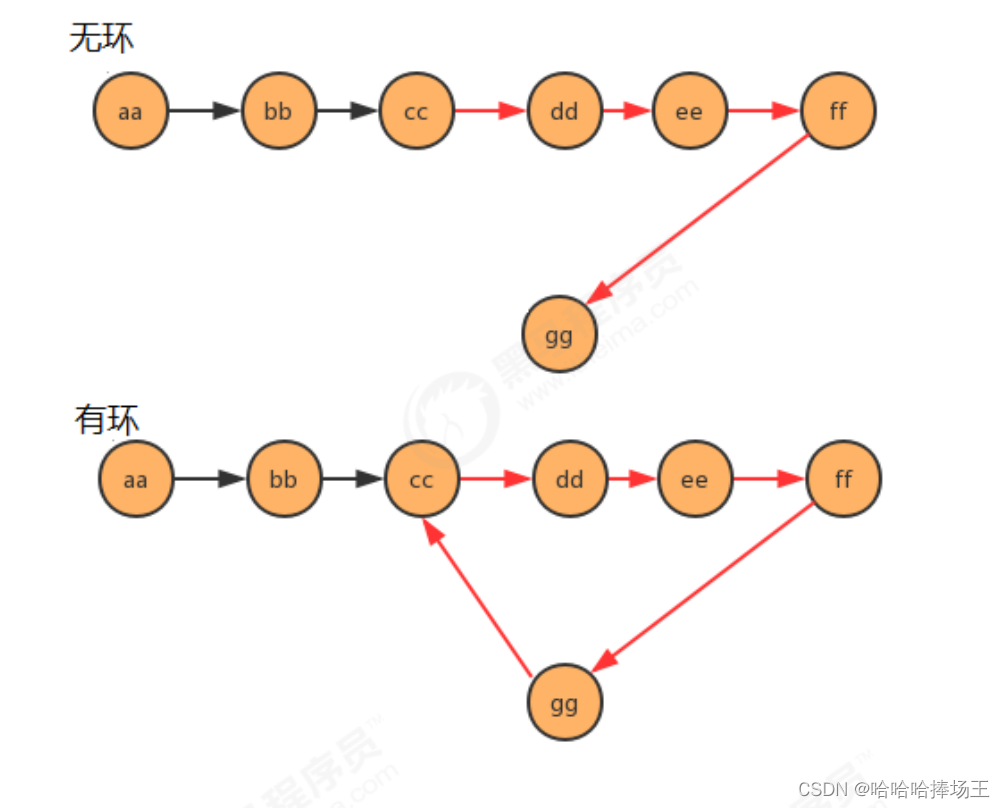
package com.tiger.study.DataStructure.Test;

public class FastSlowTestLinkListCircle {
    public static void main(String[] args) throws Exception {
        Node<String> first = new Node<String>("aa", null);
        Node<String> second = new Node<String>("bb", null);
        Node<String> third = new Node<String>("cc", null);
        Node<String> fourth = new Node<String>("dd", null);
        Node<String> fifth = new Node<String>("ee", null);
        Node<String> six = new Node<String>("ff", null);
        Node<String> seven = new Node<String>("gg", null);
        //完成结点之间的指向
        first.next = second;
        second.next = third;
        third.next = fourth;
        fourth.next = fifth;
        fifth.next = six;
        six.next = seven;
        //产生环
        seven.next = third;
        //判断链表是否有环
        boolean circle = isCircle(first);
        System.out.println("first链表中是否有环："+circle);
    }
    /**
     * 判断链表中是否有环
     * @param first 链表首结点
     * @return ture为有环，false为无环
     */
    public static boolean isCircle(Node<String> first) {
        Node<String> fast = first;
        Node<String> slow = first;
        while (fast != null && fast.next != null  ) {
            fast = fast.next.next;
            slow = slow.next;
            if (fast.equals(slow)) {
                return true;
            }
        }
        return false;
    }
    //结点类
    private static class Node<T> {
        //存储数据
        T item;
        //下一个结点
        Node next;
        public Node(T item, Node next) {
            this.item = item;
            this.next = next;
        }
    }
}

• 有环链表出口问题：

package com.tiger.study.DataStructure.Test;

public class FastSlowTestLinkListCircleExit {
    public static void main(String[] args) throws Exception {
        Node<String> first = new Node<String>("aa", null);
        Node<String> second = new Node<String>("bb", null);
        Node<String> third = new Node<String>("cc", null);
        Node<String> fourth = new Node<String>("dd", null);
        Node<String> fifth = new Node<String>("ee", null);
        Node<String> six = new Node<String>("ff", null);
        Node<String> seven = new Node<String>("gg", null);
        //完成结点之间的指向
        first.next = second;
        second.next = third;
        third.next = fourth;
        fourth.next = fifth;
        fifth.next = six;
        six.next = seven;
        //产生环
        seven.next = third;
        //判断链表是否有环
        Node circle = isCircle(first);
        System.out.println("first链表中环的入口："+circle.item);
    }
    /**
     * 检测链表环的入口
     * @param first 链表首结点
     */
    public static Node isCircle(Node<String> first) {
        Node<String> fast = first;
        Node<String> slow = first;
        Node<String> temp = null;
        while (fast != null && fast.next != null  ) {
            fast = fast.next.next;
            slow = slow.next;
            if (fast.equals(slow)) {
                temp = first;
                continue;
            }
            if (temp != null) {
                temp = temp.next;
                if (temp.equals(slow)) {
                    break;
                }
            }
        }
        return temp;
    }
    //结点类
    private static class Node<T> {
        //存储数据
        T item;
        //下一个结点
        Node next;
        public Node(T item, Node next) {
            this.item = item;
            this.next = next;
        }
    }
}

1.2.6 循环链表

• 循环链表：链表的整体形成了一个圆环状。在单向链表中，最后一个结点的指针为null，不指向任何结点，因为没有下一个元素。要实现循环链表，我们只需要让单向链表的最后一个结点的指针指向头结点即可。
  
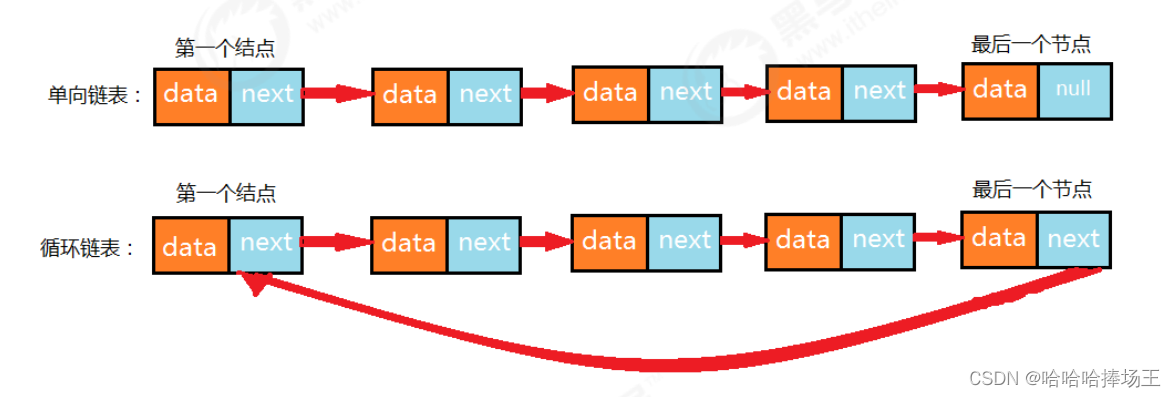• 约瑟夫问题：传说有这样一个故事，在罗马人占领乔塔帕特后，39 个犹太人与约瑟夫及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，第一个人从1开始报数，依次往后，如果有人报数到3，那么这个人就必须自杀，然后再由他的下一个人重新从1开始报数，直到所有人都自杀身亡为止。然而约瑟夫和他的朋友并不想遵从。于是，约瑟夫要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置，从而逃过了这场死亡游戏 。

package com.tiger.study.DataStructure.Test;

// 循环链表解决约瑟夫问题

public class JosephusProblemCircleLinkList {
    public static void main(String[] args) {
        // 构建循环链表包含41个结点，分别存储1-41之间的值
        Node<Integer> first = null;  // 用于记录首结点
        Node<Integer> pre = null;
        for (int i = 1; i <= 41; i++) {
            if (i == 1) {
                first = new Node<>(i, null);
                pre = first;
            } else if (i != 1 && i != 41) {
                pre.next = new Node<>(i, null);
                pre = pre.next;
            } else if (i == 41) {
                pre.next = new Node<>(i, first);
            }
        }

        // 需要count计数器，模拟报数
        int count = 0;

        // 遍历循环链表
        Node<Integer> n = first;  // 记录每次遍历拿到的结点
        Node<Integer> before = null;  // 记录当前结点的上一个结点
        while (n != n.next) {
            // 模拟报数
            count++;
            if (count == 3) {
                // 判断当前报数是3，是就删除并打印当前结点，重置count，让当前结点后移
                System.out.println("当前删除的元素是：" + n.item);
                n = n.next;
                before.next = n;
                count = 0;
            } else {
                // 如果不是3，让before变为当前结点，让当前结点后移
                before = n;
                n = n.next;
            }

        }
        System.out.println("剩余的元素是：" + n.item);
    }

    // 结点类
    private static class Node<T> {
        // 存储元素
        public T item;

        // 指向下一个结点
        public Node next;

        public Node(T item, Node next) {
            this.item = item;
            this.next = next;
        }
    }
}

1.3 栈

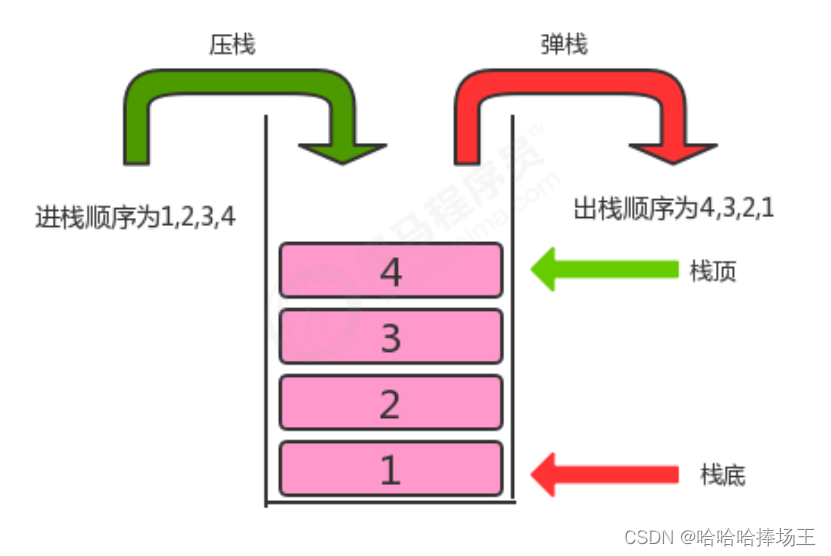
• 概念：栈是一种基于先进后出的数据结构，是一种只能在一端进行插入和删除操作的特殊线性表。它按照先进后厨的原则存储数据，先进入的数据被压入栈底，最后的数据在栈顶，需要读数据的时候从栈顶开始弹出数据。数据进入栈称为压栈，数据从栈中出去的动作为弹栈。
  
• 栈的API设计
  
• 栈代码实现

package com.tiger.study.DataStructure.Linear;

import java.util.Iterator;

public class Stack<T> implements Iterable<T>{
    // 记录栈的首结点
    private Node head;

    // 记录栈中的元素个数
    private int N;

    @Override
    public Iterator iterator() {
        return new SIterator();
    }

    private class SIterator implements Iterator {
        private Node n;

        public SIterator() {
            this.n = head;
        }

        @Override
        public boolean hasNext() {
            return n.next != null;
        }

        @Override
        public Object next() {
            n = n.next;
            return n.item;
        }
    }

    private class Node {
        public T item;
        public Node next;

        public Node(T item, Node next) {
            this.item = item;
            this.next = next;
        }

    }

    public Stack() {
        this.head = new Node(null, null);
        this.N = 0;
    }

    // 判断当前栈中的元素个数是否为0
    public boolean isEmpty() {
        return this.N == 0;
    }

    // 获取栈中的元素的个数
    public int size() {
        return this.N;
    }

    // 把t元素压入栈
    public void push(T t) {
        // 找到首结点指向的第一个结点
        Node newNode = new Node(t, this.head.next);
        this.head.next = newNode;
        this.N++;
    }

    // 弹出栈顶元素
    public T pop() {
        // 找到首结点指向的第一个元素，记录
        Node popNode = this.head.next;
        if (popNode == null) {
            return null;
        }
        // 将首结点指向原来第一个结点的下一个结点
        this.head.next = popNode.next;
        this.N--;
        return popNode.item;
    }

}

• 括号比配：给定一个字符串，里边可能包含"()"小括号和其他字符，编写程序查看小括号是否成对出现

package com.tiger.study.DataStructure.Test;

import com.tiger.study.DataStructure.Linear.Stack;

public class BracketsMatchTest {
    public static void main(String[] args) {
        String str = "(上海(长安)))";
        boolean match = isMatch(str);
        System.out.println(match);


    }

    // 判断str的括号是否匹配
    public static boolean isMatch(String str) {
        char[] chars = str.toCharArray();
        Stack<Character> stack = new Stack<>();
        for (char aChar : chars) {
            if (aChar == '(') {
                stack.push(aChar);
            } else if (aChar == ')') {
                if (stack.size() == 0) {
                    return false;
                } else {
                    stack.pop();
                }
            }
        }
        if (stack.size() != 0) {
            return false;
        }

        return true;
    }

}

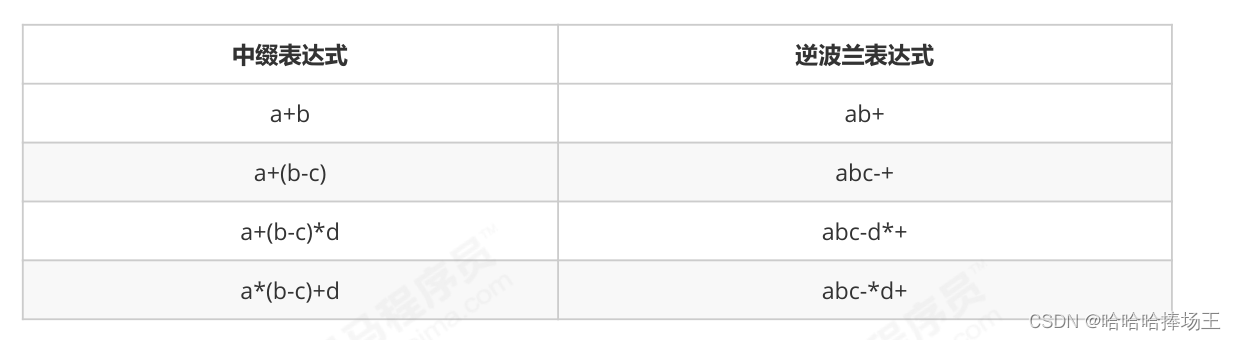
• 逆波兰表达式：求值
  • 中缀表达式：二元运算符总是置于两个操作数之间。
  • 逆波兰表达式（后缀表达式）：运算符总是放在跟它相关的操作数之后
    

package com.tiger.study.DataStructure.Test;

import com.tiger.study.DataStructure.Linear.Stack;

public class ReversePolishNotationTest {
    public static void main(String[] args) {
        // 中缀表达式3*(17-15)+18/6的逆波兰表达式如下：
        String[] notation = {"3", "17", "15", "-", "*", "18", "6", "/", "+"};

        System.out.println(calculate(notation));
    }

    // 计算逆波兰表达式结果
    public static int calculate(String[] strs) {
        // 定义一个栈，用来存储操作数
        Stack<Integer> oprands = new Stack<>();
        // 从左往右遍历逆波兰表达式，得到每一个元素
        for (int i = 0; i < strs.length; i++) {
            String curr = strs[i];
            // 判断当前元素是运算符还是操作数
            Integer o1;
            Integer o2;
            switch (curr) {
                // 运算符，从栈中弹出两个操作数，完成运算，运算完成的结果再压入栈中
                case "+":
                    o1 = oprands.pop();
                    o2 = oprands.pop();
                    oprands.push(o2 + o1);
                    break;
                case "-":
                    o1 = oprands.pop();
                    o2 = oprands.pop();
                    oprands.push(o2 - o1);
                    break;
                case "*":
                    o1 = oprands.pop();
                    o2 = oprands.pop();
                    oprands.push(o2 * o1);
                    break;
                case "/":
                    o1 = oprands.pop();
                    o2 = oprands.pop();
                    oprands.push(o2 / o1);
                    break;
                // 操作数，把该操作数放入到栈中
                default:
                    oprands.push(Integer.parseInt(curr));
                    break;
            }
        }

        // 得到栈中最后一个元素，就是逆波兰表达式的结果
        return oprands.pop();
    }
}

1.4 队列

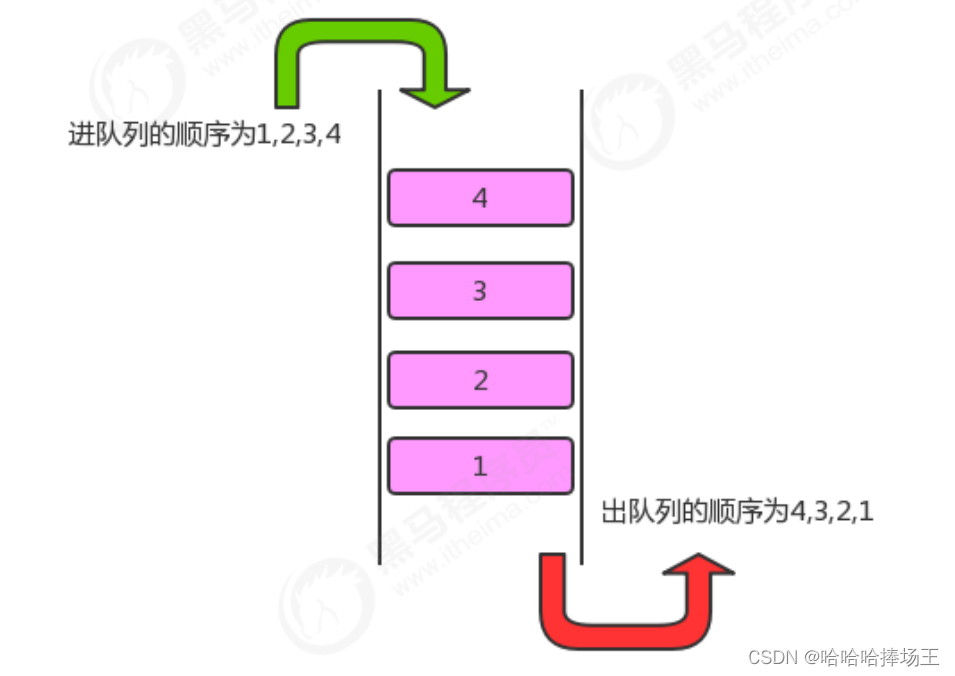
• 队列是一种基于先进先出的数据结构，是一种只能在一端进入，另一端删除的特殊线性表，它按照先进先出的原则存储数据，先进入的数据，在读取数据时先被读出来。
  
• 队列的API设计
  
• 代码实现

package com.tiger.study.DataStructure.Linear;

import java.util.Iterator;

public class Queue<T> implements Iterable<T>{
    // 头节点
    private Node head;

    // 尾结点
    private Node last;

    // 对列长度
    private int N;

    @Override
    public Iterator<T> iterator() {
        return new QIterator();
    }
    private class QIterator implements Iterator {
        private Node n;

        public QIterator() {
            this.n = head;
        }

        @Override
        public boolean hasNext() {
            return n.next != null;
        }

        @Override
        public Object next() {
            n = n.next;
            return n.item;
        }
    }

    private class Node {
        public T item;
        public Node next;

        public Node(T item, Node next) {
            this.item = item;
            this.next = next;
        }
    }

    public Queue() {
        this.head = new Node(null, null);
        this.last = null;
        this.N = 0;
    }

    // 判断队列是否为空
    public boolean isEmpty() {
        return this.N == 0;
    }

    // 返回队列中元素的个数
    public int size() {
        return this.N;
    }

    // 向队列中插入元素
    public void enqueue(T t) {
        Node newNode = new Node(t, null);
        if (last == null) {
            last = newNode;
            head.next = newNode;
        } else {
            last.next = newNode;
            last = newNode;
        }
        this.N++;
    }

    // 从队列中拿出一个元素
    public T dequeue() {
        if (isEmpty()) {
            return null;
        }
        Node curr = head.next;
        head.next = curr.next;
        this.N--;
        if (isEmpty()) {
            last = null;
        }
        return curr.item;
    }
}