一. 问题描述

博物馆大盗问题：
大盗潜入博物馆，面前有5件宝物，分别有重量和价值，大盗的背包仅能负重20公斤，请问如何选择宝物，总价值最高？

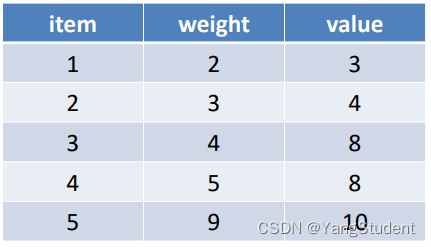
贪心算法的策略就是：

先装价值最大的 10 对应的宝物，就剩下20 - 9 = 11
再装价值第二大的 8 对应的宝物，就剩下11 - 5 = 6
再装价值还是 8 对应的宝物，就只剩下 6 - 4 = 2
再装价值是 4 的宝物，3 > 2就装不下了

贪心算法的结果就是 10 + 8 + 8 = 26
而实际的情况是，还可以再装以一个价值为3的宝物，能装的最大价值是29。
因此，贪心算法不能解决这样的问题。

二. 动态规划解法

我们把 $m (i, W)$ 记为：
前i(1<=i<=5)个宝物中，组合的重量不超过W(1<=W<=20) 重量，得到的最大价值。

$m (i, W)$ 应该是 $m (i ? 1, W)$ 和 $m (i ? 1, W ? Wi) + v i$ 两者最大值。

$m (i ? 1, W)$ 就是已经装不下其他的宝物的情况，因为此时，如果加上第i件宝物的话，就会超重了。所以此时，m(i,W) 就等于 m(i-1, W)。

$m(i-1,W-Wi) + v_i$ 就是当第i个宝物可以加入到组合中，加上第i个宝物后的重量小于W，此时 $m (i, W)$ 就等于前i-1件宝物的价值，加上第i件宝物的价值。

所以 $m (i, W)$ 如下所示：
$m(i,W)=\left\{ \begin{aligned} 0 \quad if\ i=0\\ 0 \quad if\ W=0\\ m(i-1,W) \quad if\ w_i>W\\ max\{m(i-1,W),v_i+m(i-1,W-w_i)\}\quad otherwise \end{aligned} \right .$
第一种情况，就是收集0个宝物，最大的价值就是0。
第二种情况，最多只能背起0公斤的宝物，最大的价值就是0。
第三种情况，第i件宝物的重量比负重还大，那肯定不能加了。
第四种情况，就是上面说的情况。

动态规划的思想就是，求出一个小问题的最优解，然后将规模变大，根据上一个小问题的最优解继续求出更大规模的问题的最优解，直到所要求的目标规模，就求出来了动态规划的最优解。

在求解的时候，可以通过画表格，填数字，来呈现出这样的一个解决问题的过程。

我们从 $m (1, 1)$ 计算到 $m (5, 20)$ 。

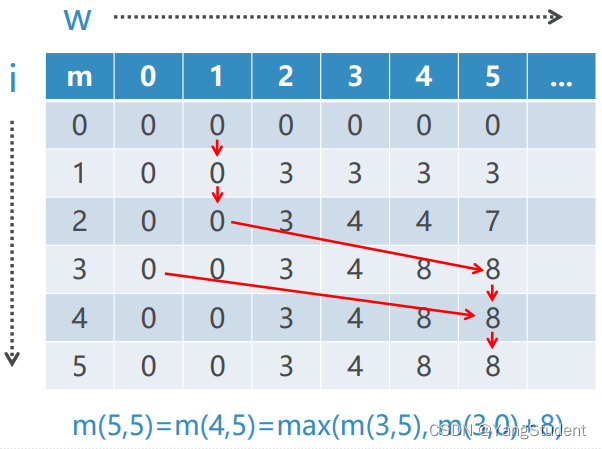
首先我们定义这个问题，方便下面进行计算和求解。

# 宝物的重量和价值
treasure = [None,
            {'w': 2, 'v': 3},
            {'w': 3, 'v': 4},
            {'w': 4, 'v': 8},
            {'w': 5, 'v': 8},
            {'w': 9, 'v': 10}]
# None是用于保存0个宝物或0个重量的情况

# 大盗的最大负重
max_w = 20

初始化这个表格，根据行数和列数，生成一个全是0的表格

m = [[0] * (max_w + 1)] * len(treasure)

开始填表，根据上文的分析，第一行 $m (0, w)$ 和 $一列 m (i, 0)$ 所有的数据都是0。
第一件宝物的最轻，是2，显然当 $W = 1$ 的时候，还是什么宝物都装不下。所以第二列也全都是0。
所以我们应该从第二行，第三列开始填表。
第一个就是 $m (1, 2)$ 即m[1][2]

for i in range(1, len(treasure)):
    for W in range(2, max_w + 1):
        w_i = treasure[i]['w']
        if w_i > W: # 装不下第i个宝物
            m[i][W] = m[i - 1][W] # 不装第i个宝物
        else:
            v_i = treasure[i]['v'] # 第i个宝物的价值
            m[i][W] = max(m[i - 1][W], m[i - 1][W - w_i] + v_i) # 装和不装第i个宝物的最大值
        # print(m)
        # 套用上面的公式

测试结果

# print(m)
print(m[5][5])
print(m[5][20])

8
29

完整代码：

from time import process_time

t_start = process_time()
# 宝物的重量和价值
treasure = [None,
            {'w': 2, 'v': 3},
            {'w': 3, 'v': 4},
            {'w': 4, 'v': 8},
            {'w': 5, 'v': 8},
            {'w': 9, 'v': 10}]  # 10 + 16 + 3
# None是用于保存0个宝物或0个重量的情况

# 大盗的最大负重
max_w = 20

# 初始化表格，全都是0
m = [[0] * (max_w + 1) for _ in range(len(treasure))]
# print(m)
# print(len(m))

# 开始填表，根据上文的分析，第一行$m(0,w)$和$一列m(i, 0)$所有的数据都是0。
# 第一件宝物的最轻，重量是2，显然当$W = 1$的时候，还是什么宝物都装不下。所以第二列也全都是0。
# 所以我们应该从第二行，第三列开始填表。

for i in range(1, len(treasure)):
    for W in range(2, max_w + 1):
        w_i = treasure[i]['w']
        if w_i > W:  # 装不下第i个宝物
            m[i][W] = m[i - 1][W]  # 不装第i个宝物
        else:
            v_i = treasure[i]['v']  # 第i个宝物的价值
            m[i][W] = max(m[i - 1][W], m[i - 1][W - w_i] + v_i)  # 装和不装第i个宝物的最大值
        # print(m)
        # 套用上面的公式

# print(m)
print(m[5][5])
print(m[5][20])

t_end = process_time()
print("Start time: ", t_start)
print("Finish time: ", t_end)
print("The whole program use %d seconds.", t_end - t_start)

三. 递归解法

from time import process_time

t_start = process_time()

treasure = {(2, 3), (3, 4), (4, 8), (5, 8), (9, 10)}

m = {}  # 初始化记忆化表格 m{((tri, trj, ..., trz), wa): value1, ((tr1, tr2, ...., trn), wb): value2, ....}


# m的key是 (宝物的组合, 最大重量)，value

def museum_big_thief_problem(w, tr):  # w可负重，tr是宝物列表，依次遍历宝物的列表
    if tr == set() or w == 0:  # 基本结束条件 加上最后一件宝物时，重量不够用了，列表里面的宝物都算过了
        m[(tuple(tr), w)] = 0
        return 0
    elif (tuple(tr), w) in m:  # 搜索记忆化表格已经存储的数据
        return m[(tuple(tr), w)]
    else:
        v_max = 0  # v_max用于存储中间结果。初始化为0。
        for item in tr:
            if item[0] <= w:  # 当前宝物的重量小于可用重量
                v = museum_big_thief_problem(w - item[0], tr - {item}) + item[1]  # 前面的最大的价值 + 当前宝物的价值
                v_max = max(v, v_max)
        m[tuple(tr), w] = v_max
        return v_max
        #      朝着规模缩小的情况演进 可用的重量越来越少 / 调用自身


print(museum_big_thief_problem(20, treasure))

t_finish = process_time()
print("Start time: ", t_start)
print("Finish time: ", t_finish)
print("The program use %d seconds.", t_finish - t_start)