数据规模->时间复杂度
<=10^4 😮(n^2)
<=10^7:o(nlogn)
<=10^8:o(n)
10^8<=:o(logn),o(1)
内容

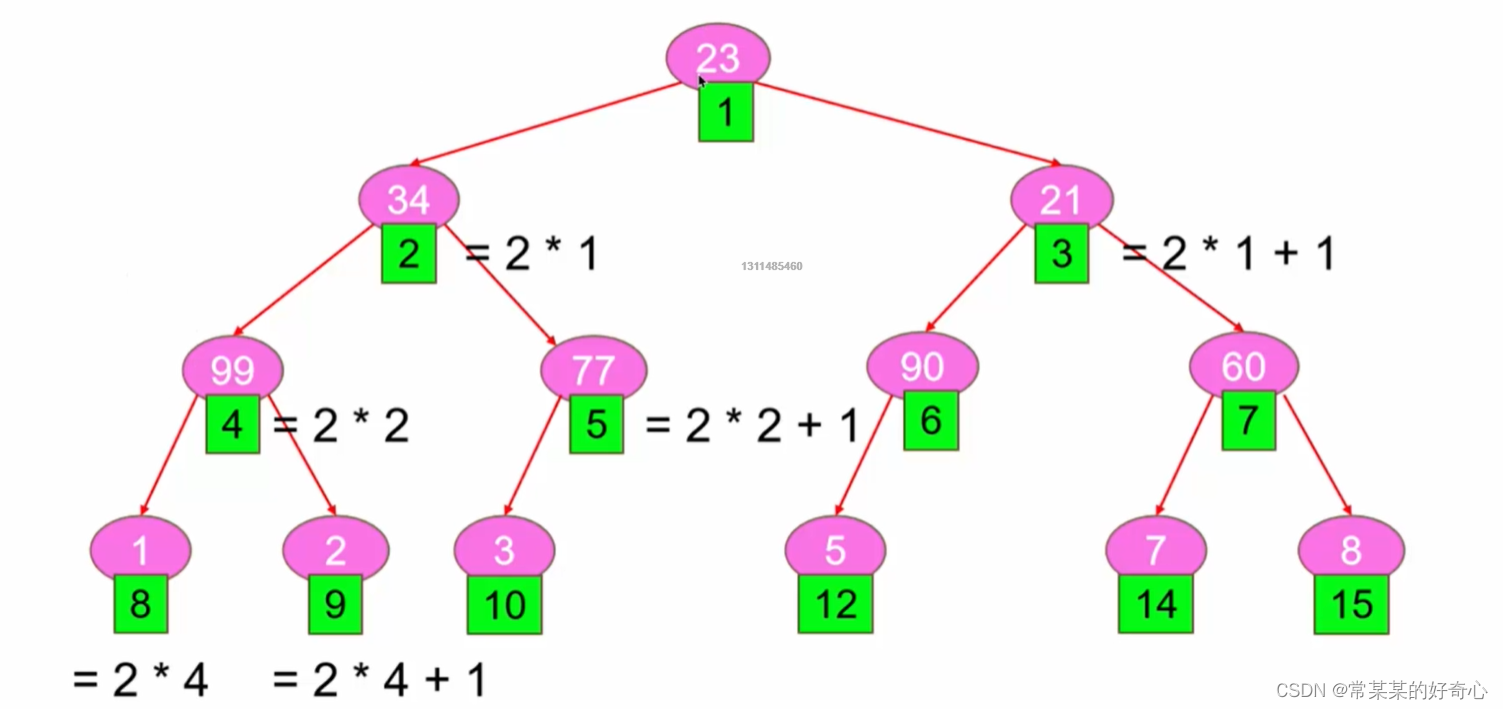
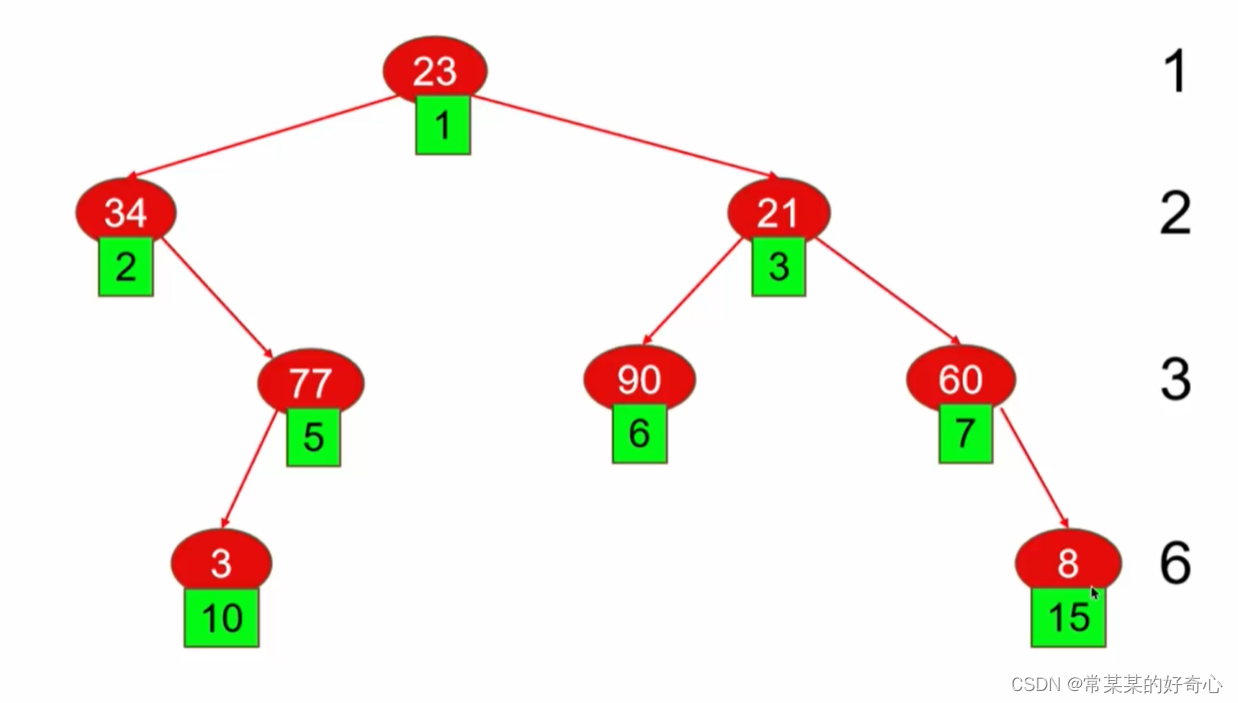
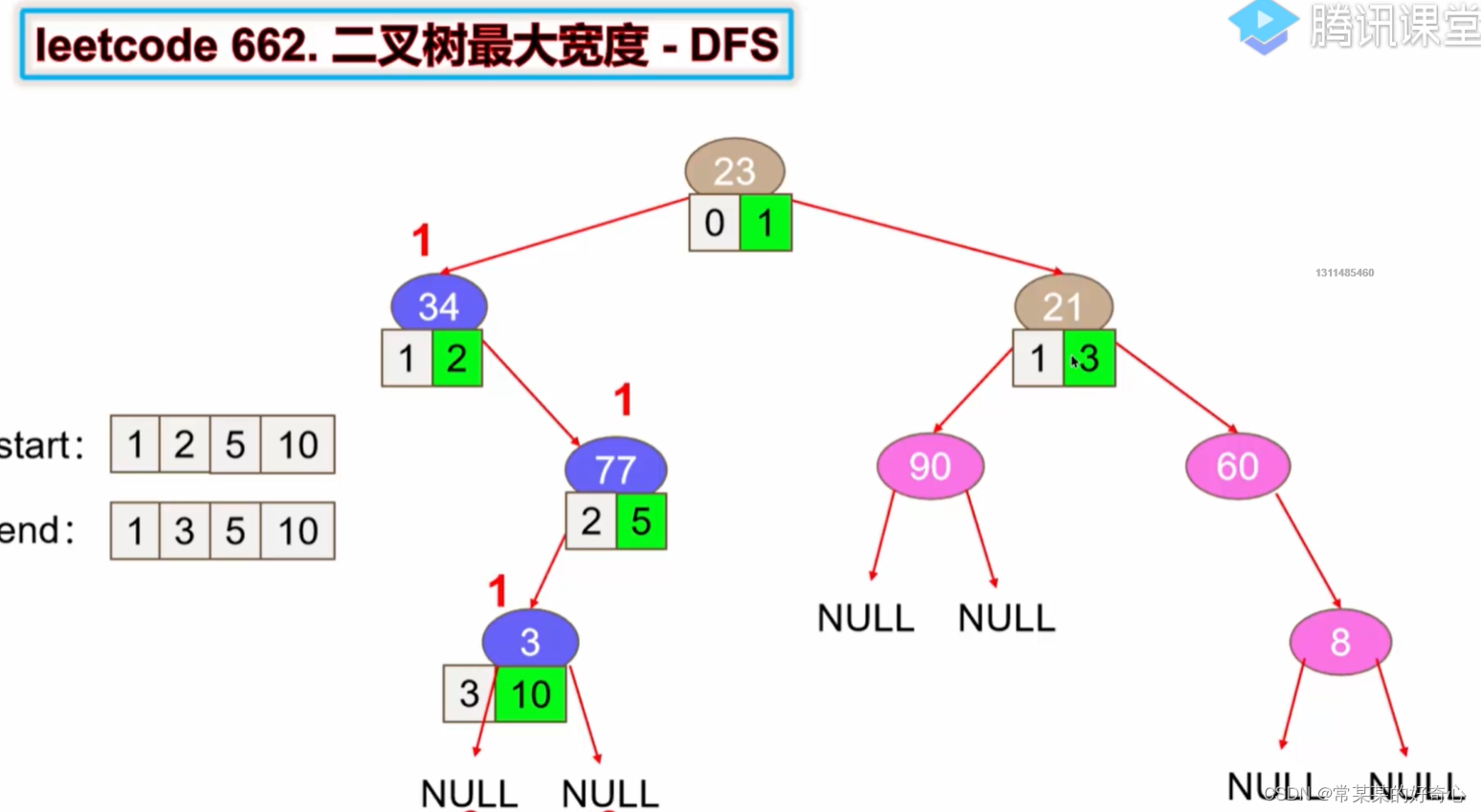
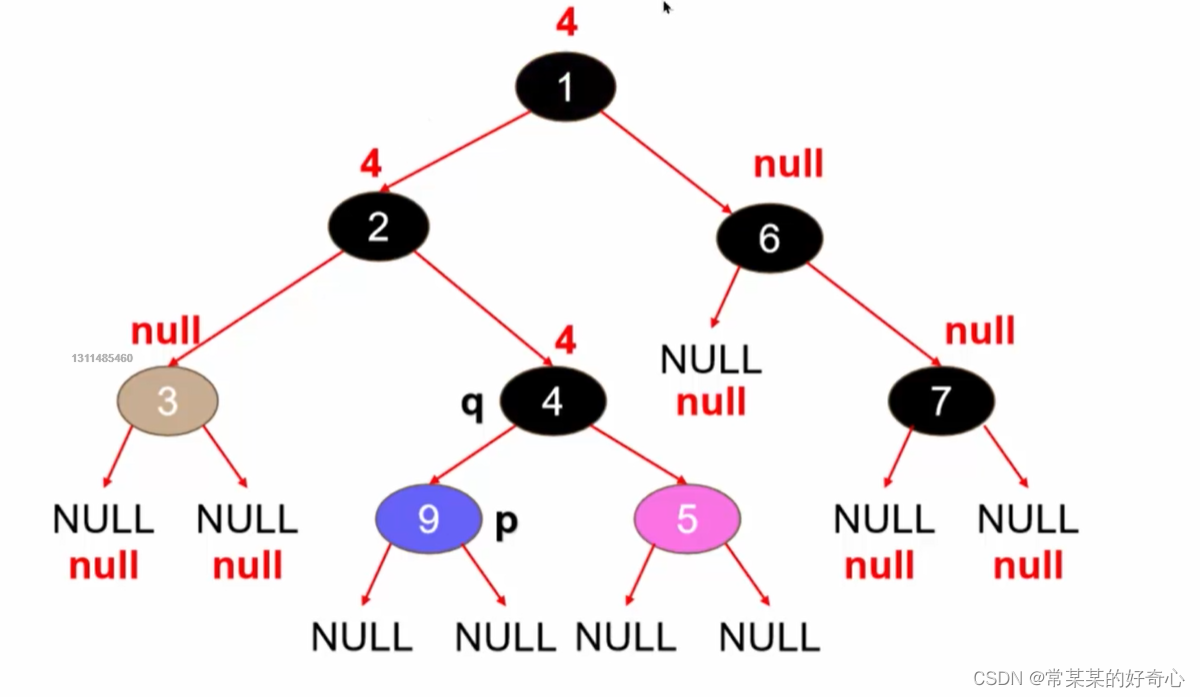
lc 662 :二叉树最大宽度
https://leetcode.cn/problems/maximum-width-of-binary-tree/
提示:
树中节点的数目范围是 [1, 3000]
-100 <= Node.val <= 100
注:两端点间会出现一些延伸到这一层的 null 节点,这些 null 节点也计入长度
#方案一:BFS
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:
queue=deque()
queue.append([root,1])
maxv=float('-inf')
while queue:
size=len(queue)
start,end=0,0
for i in range(size):
curr,currseq=queue.popleft()
if i==0:start=currseq
if i==size-1:end=currseq
#
if curr.left:queue.append([curr.left,2*currseq])
if curr.right:queue.append([curr.right,2*currseq+1])
maxv=max(maxv,end-start+1)
return maxv
#方案二:DFS
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:
if not root:return 0
return self.DFS(root,0,1,list(),list())
def DFS(self,node,currlevel,currseq,start,end):
#边递,边更新存储
if not node:return 0
if len(start)<currlevel+1:
start.append(currseq)
end.append(currseq)
else:
end[currlevel]=currseq
#
left=self.DFS(node.left,currlevel+1,2*currseq,start,end)
right=self.DFS(node.right,currlevel+1,2*currseq+1,start,end)
#边回溯,边计算最大宽度
curr_width=end[currlevel]-start[currlevel]+1
return max(curr_width,max(left,right))
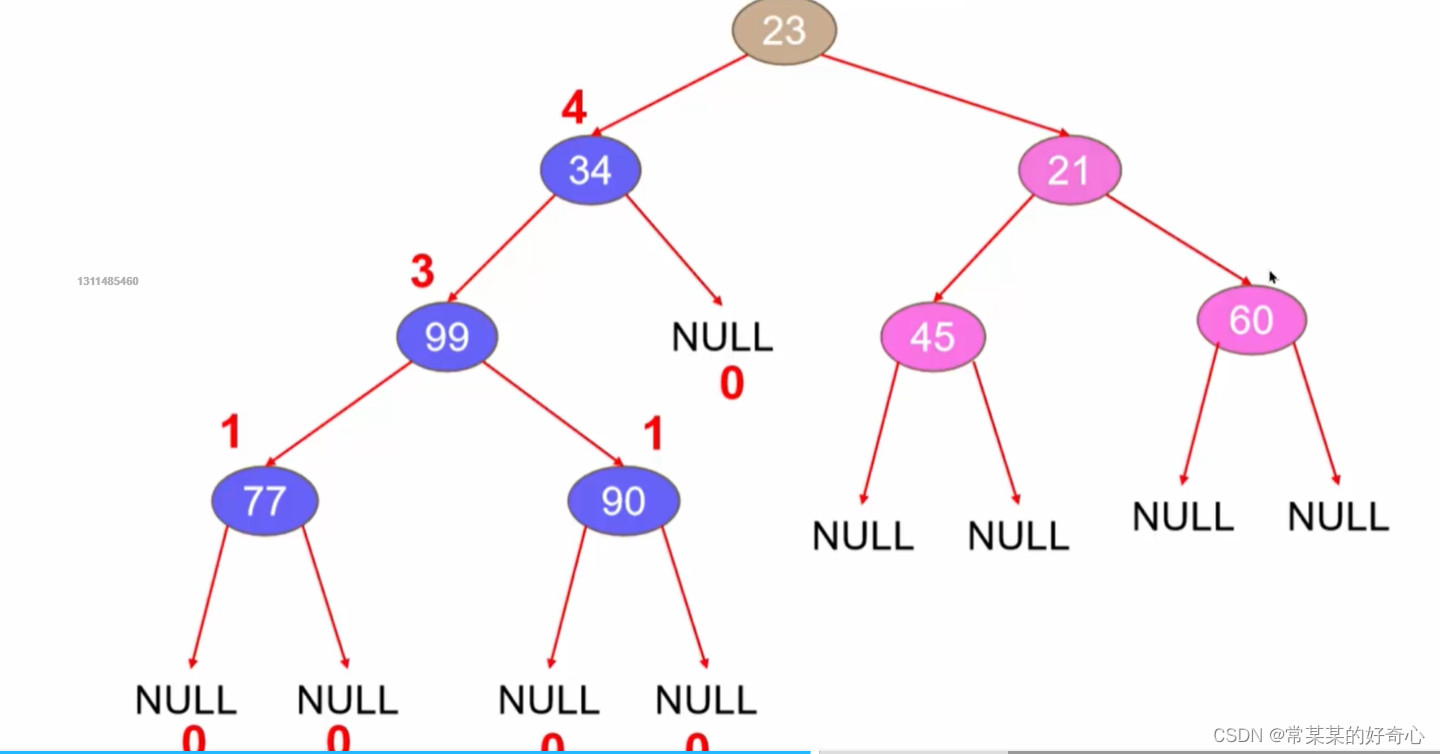
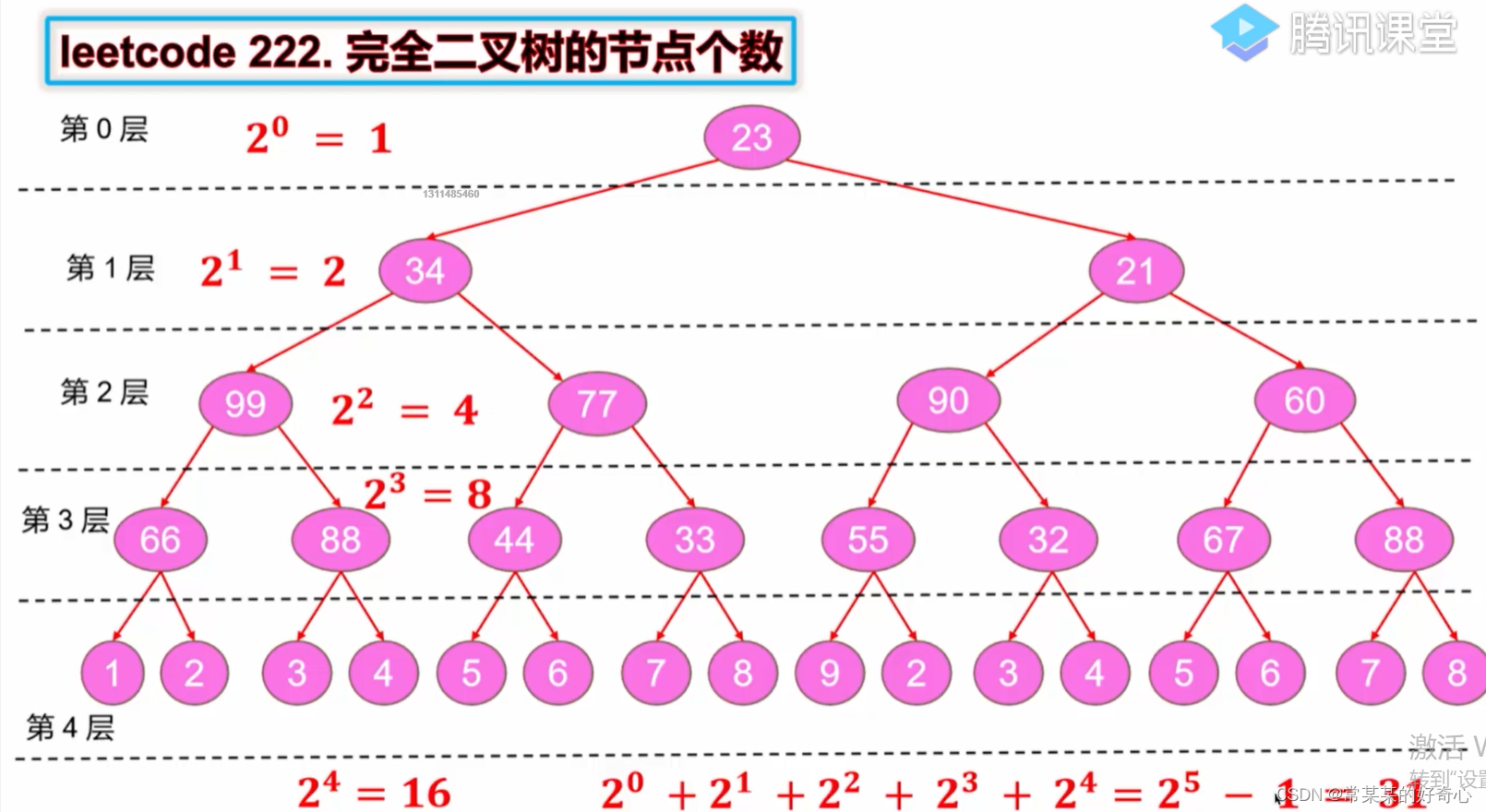
lc 222 :完全二叉树的节点个数
https://leetcode.cn/problems/count-complete-tree-nodes/
提示:
树中节点的数目范围是[0, 5 * 10^4]
0 <= Node.val <= 5 * 10^4
题目数据保证输入的树是 完全二叉树
进阶:
遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗?
#方案一:DFS
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def countNodes(self, root: Optional[TreeNode]) -> int:
if not root:return 0
return self.preorder(root)
def preorder(self,node):
if not node:return 0
#
left=self.countNodes(node.left)
right=self.countNodes(node.right)
return left+right+1
#方案二:二分查找(优化)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def countNodes(self, root: Optional[TreeNode]) -> int:
if not root:return 0
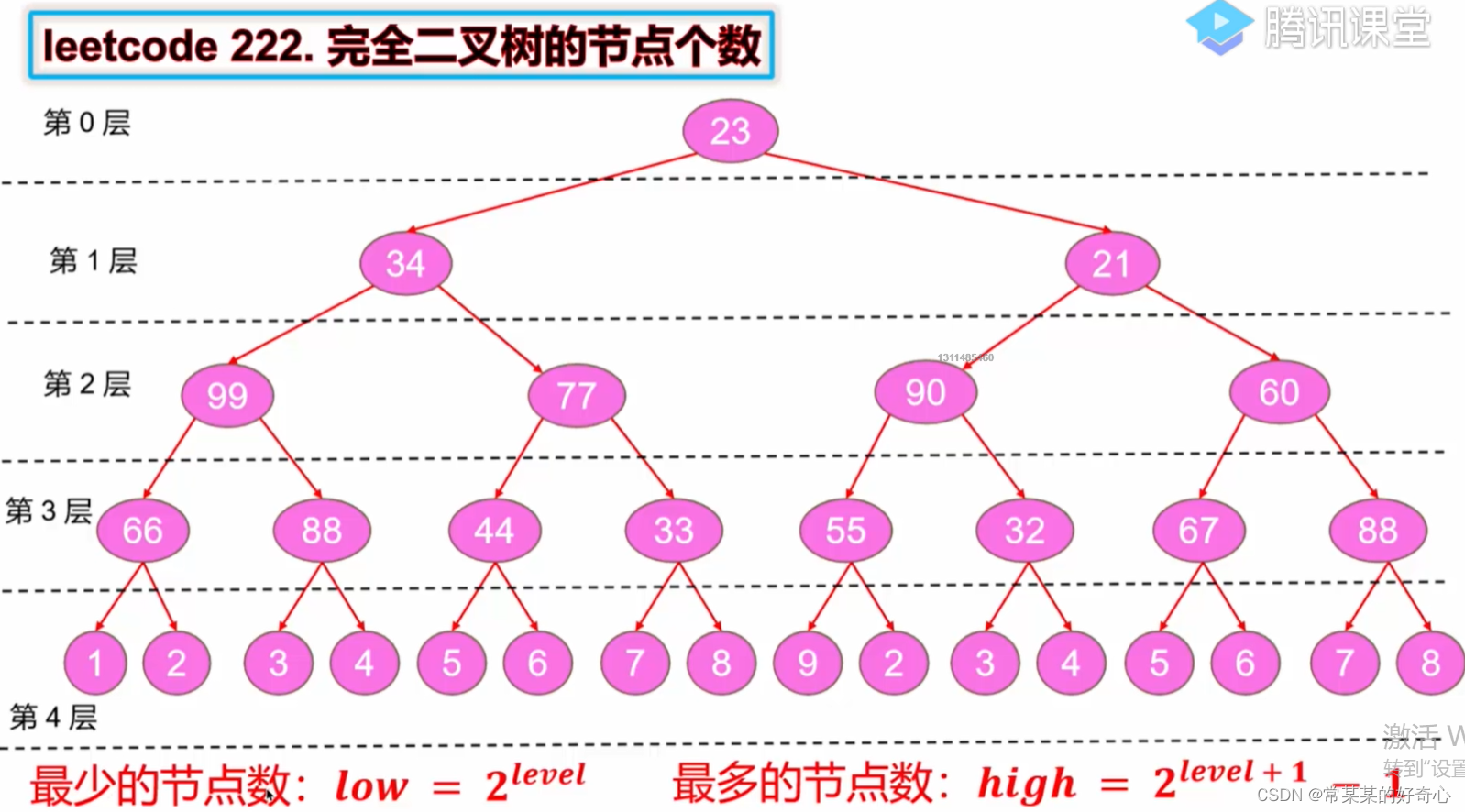
#统计层数(完全二叉树)
level=0
curr=root
while curr.left:
level+=1
curr=curr.left
#节点个数【2^level,2^(level+1)-1】
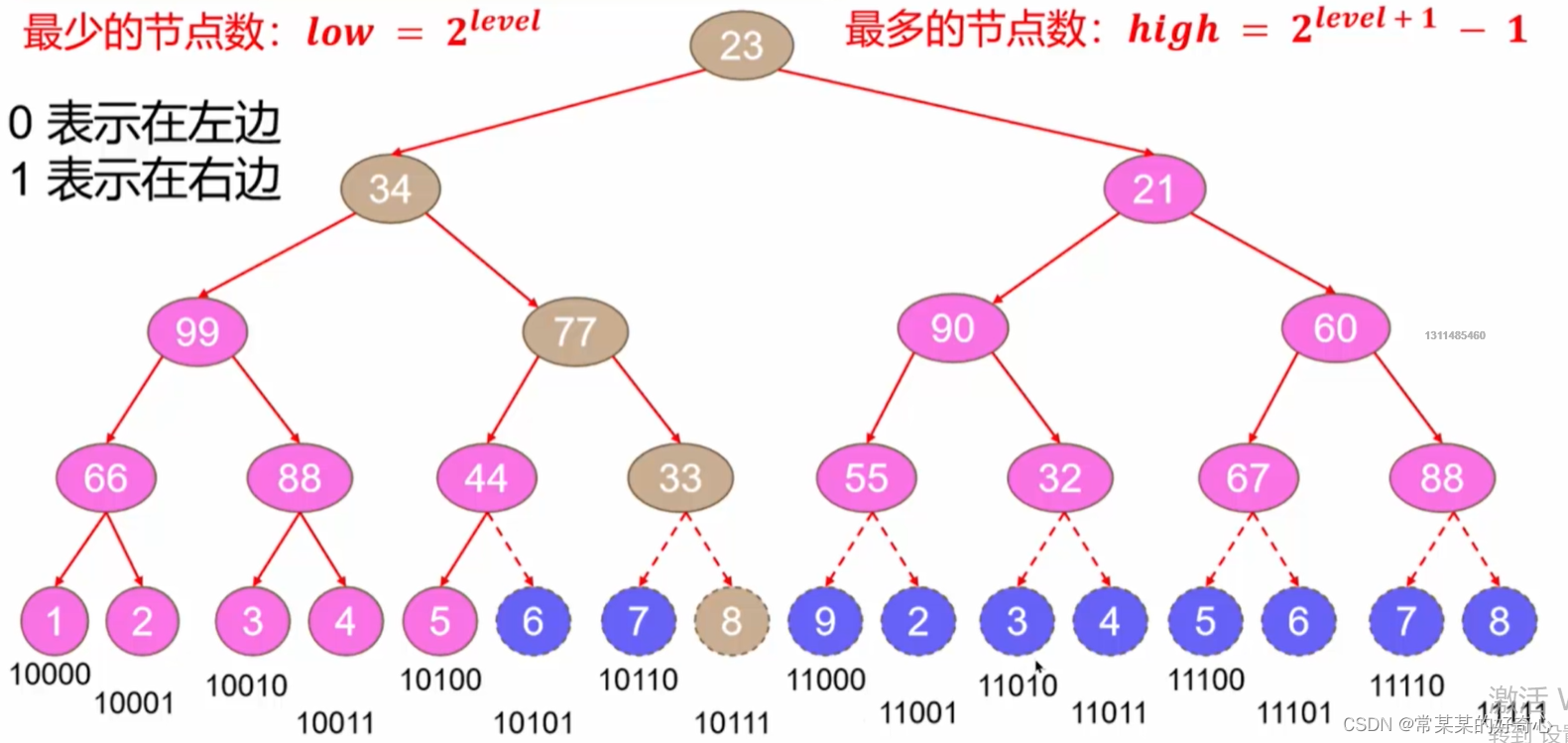
left,right=1<<level,(1<<(level+1))-1
while left<right:
mid=left+(right-left+1)//2 #+1
if self.exsit(root,level,mid):
left=mid #
else:right=mid-1
return left
def exsit(self,node,level,mid):
mask=1<<(level-1) #决定走向:例如level=4,01000
#从root开始走
while node and mask>0:
if (mask&mid)==0:
#左行
node=node.left
else:
node=node.right
mask>>=1
return node!=None
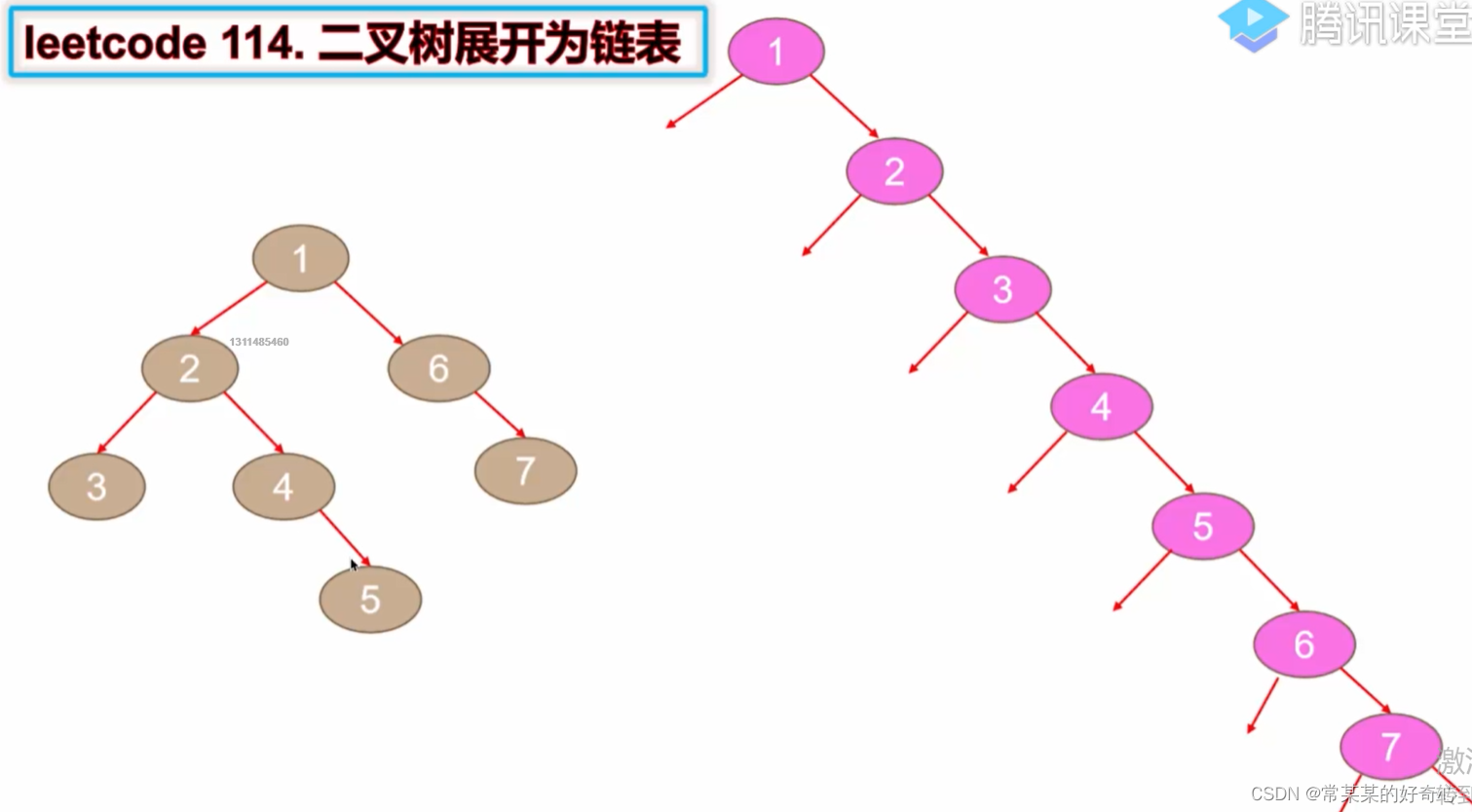
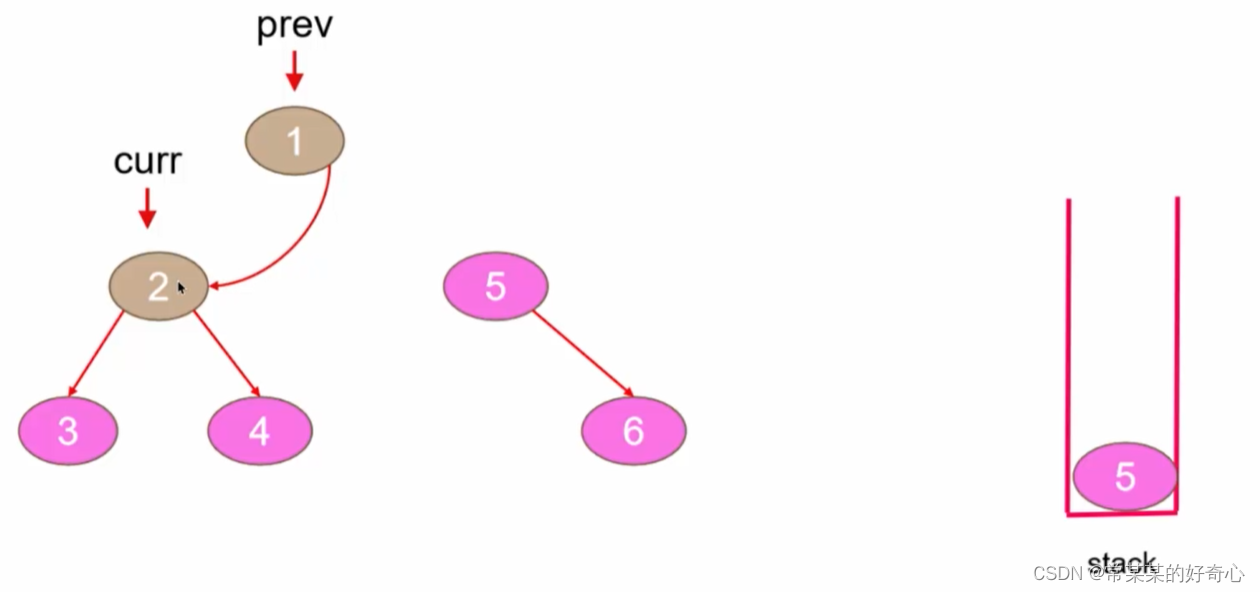
lc 114【top100】:二叉树展开为链表
https://leetcode.cn/problems/flatten-binary-tree-to-linked-list/
提示:
树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100
进阶:
你可以使用原地算法(O(1) 额外空间)展开这棵树吗?
#方案一;先前序遍历后串联
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def flatten(self, root: Optional[TreeNode]) -> None:
"""
Do not return anything, modify root in-place instead.
"""
if not root:return None
#
res=list()
self.preorder(root,res)
for i in range(1,len(res)):
curr=res[i-1]
next=res[i]
curr.left=None
curr.right=next
def preorder(self,node,res):
if not node: return None
res.append(node)
self.preorder(node.left,res)
self.preorder(node.right,res)
#方案二:边遍历边串联
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def flatten(self, root: Optional[TreeNode]) -> None:
"""
Do not return anything, modify root in-place instead.
"""
if not root:return None
#
stack=[]
stack.append(root)
prev=None
while stack:
#key
curr=stack.pop()
if prev:
prev.left=None
prev.right=curr
prev=curr
#
if curr.right:stack.append(curr.right)
if curr.left:stack.append(curr.left)
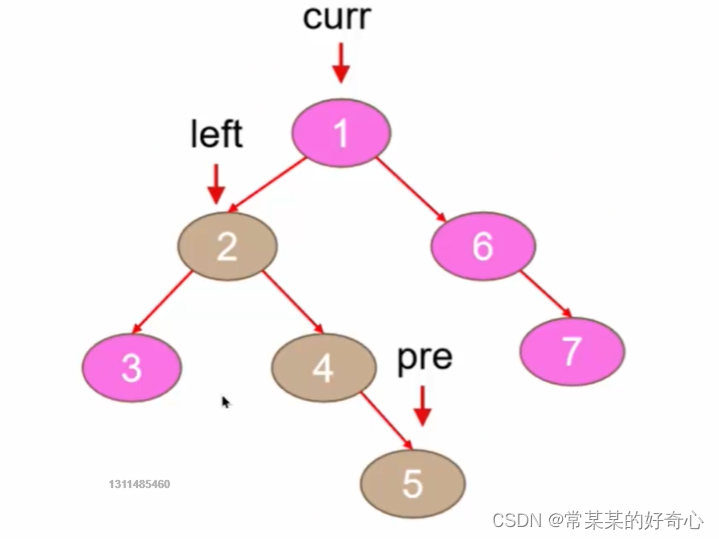
#方案三:原地改变指针(优化)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def flatten(self, root: Optional[TreeNode]) -> None:
"""
Do not return anything, modify root in-place instead.
"""
if not root:return None
#
curr=root
while curr:
left=curr.left
if left:
pre=curr.left
while pre.right:pre=pre.right
pre.right=curr.right
#
curr.left=None
curr.right=left
#
curr=curr.right
else:curr=curr.right
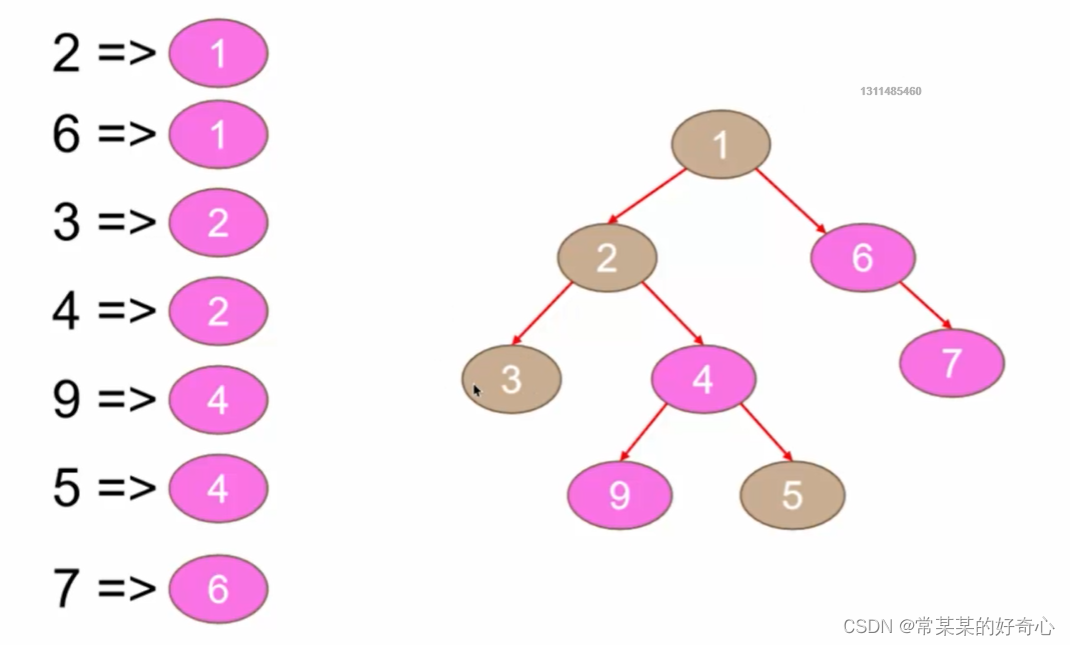
lc 236【剑指 68-2】【top100】:二叉树的最近公共祖先
https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/
提示:
树中节点数目在范围 [2, 10^5] 内。
-10^9 <= Node.val <= 10^9
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中。
#方案一:维护节点与后节点关系+前序遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
if not root:return None
#
self.par={}
self.dfs(root)
#
self.set=set()
while p:
self.set.add(p)
p=self.par.get(p.val,None)
while q:
if q in self.set:return q
q=self.par.get(q.val) #self.par[q.val]
#
return None
def dfs(self,node):
if not node:return None
#
if node.left:self.par[node.left.val]=node
if node.right:self.par[node.right.val]=node
#
self.dfs(node.left)
self.dfs(node.right)
#方案二:后序遍历(相遇时的情形)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
if not root:return None
if root==p or root==q:return root
#
left=self.lowestCommonAncestor(root.left,p,q)
right=self.lowestCommonAncestor(root.right,p,q)
if not left:return right
if not right:return left
return root
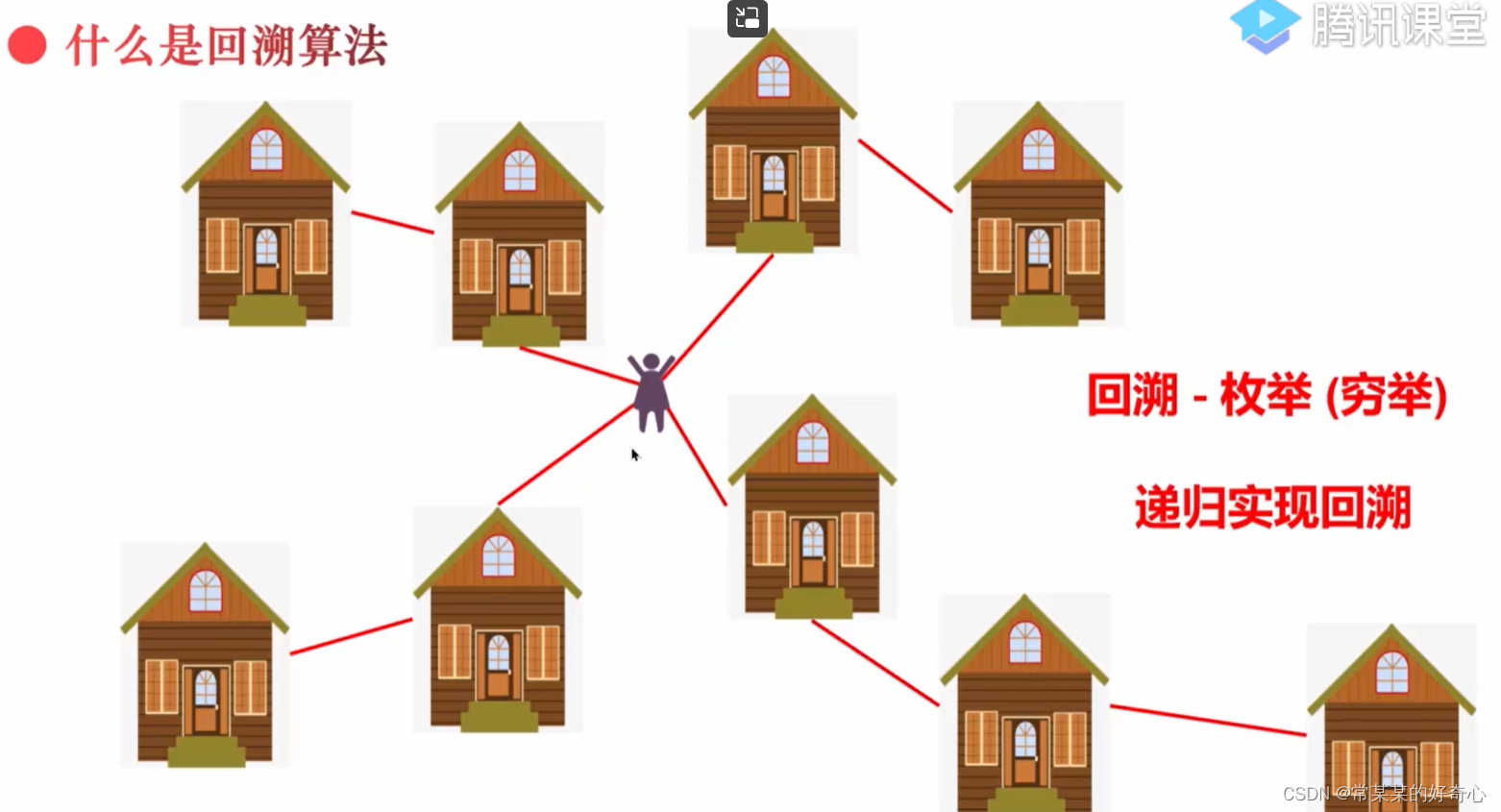
回溯思想
#回溯树的DFS
#回溯图的DFS
#本质:穷举
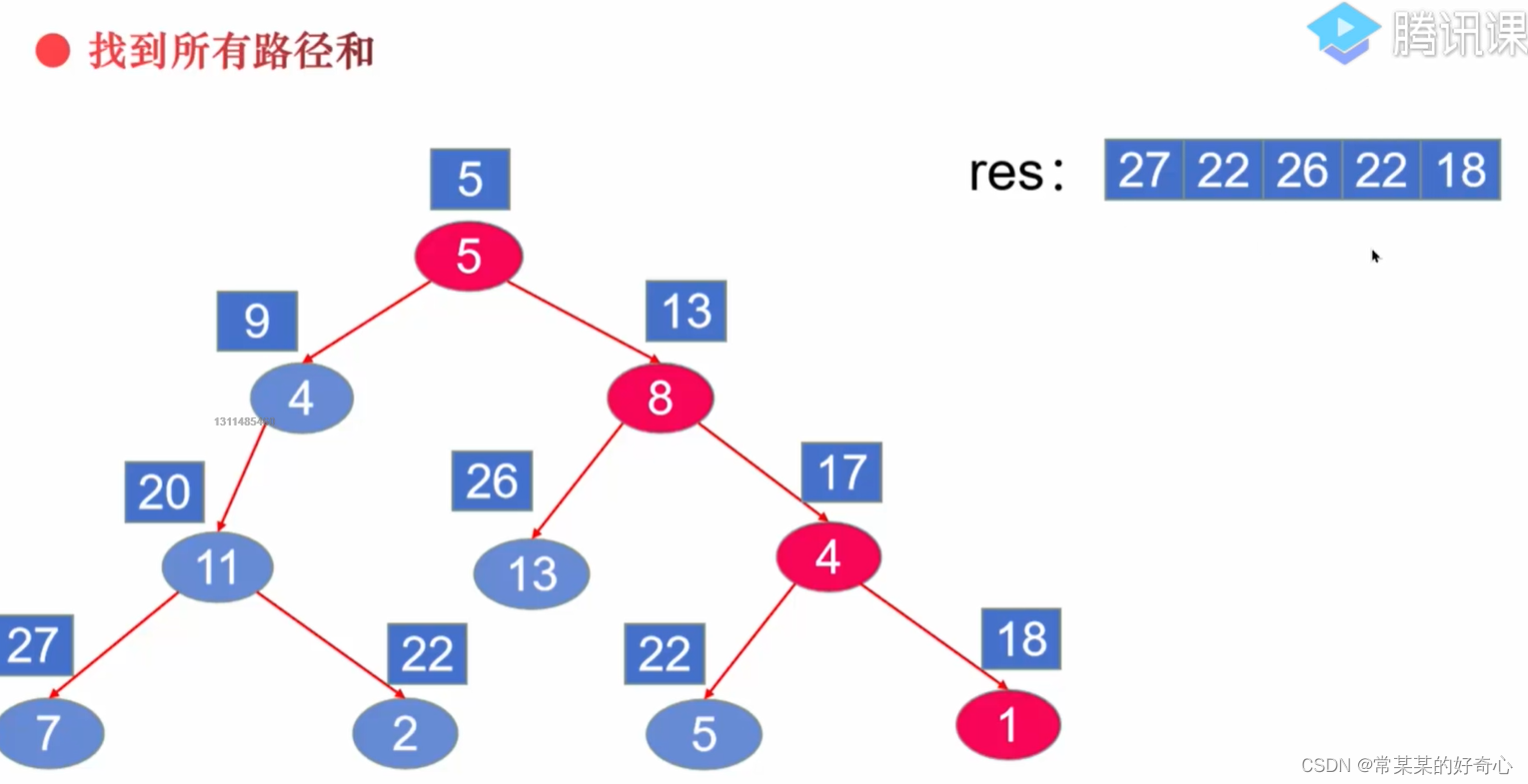
lc 112 :路径总和
https://leetcode.cn/problems/path-sum/
提示:
树中节点的数目在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000
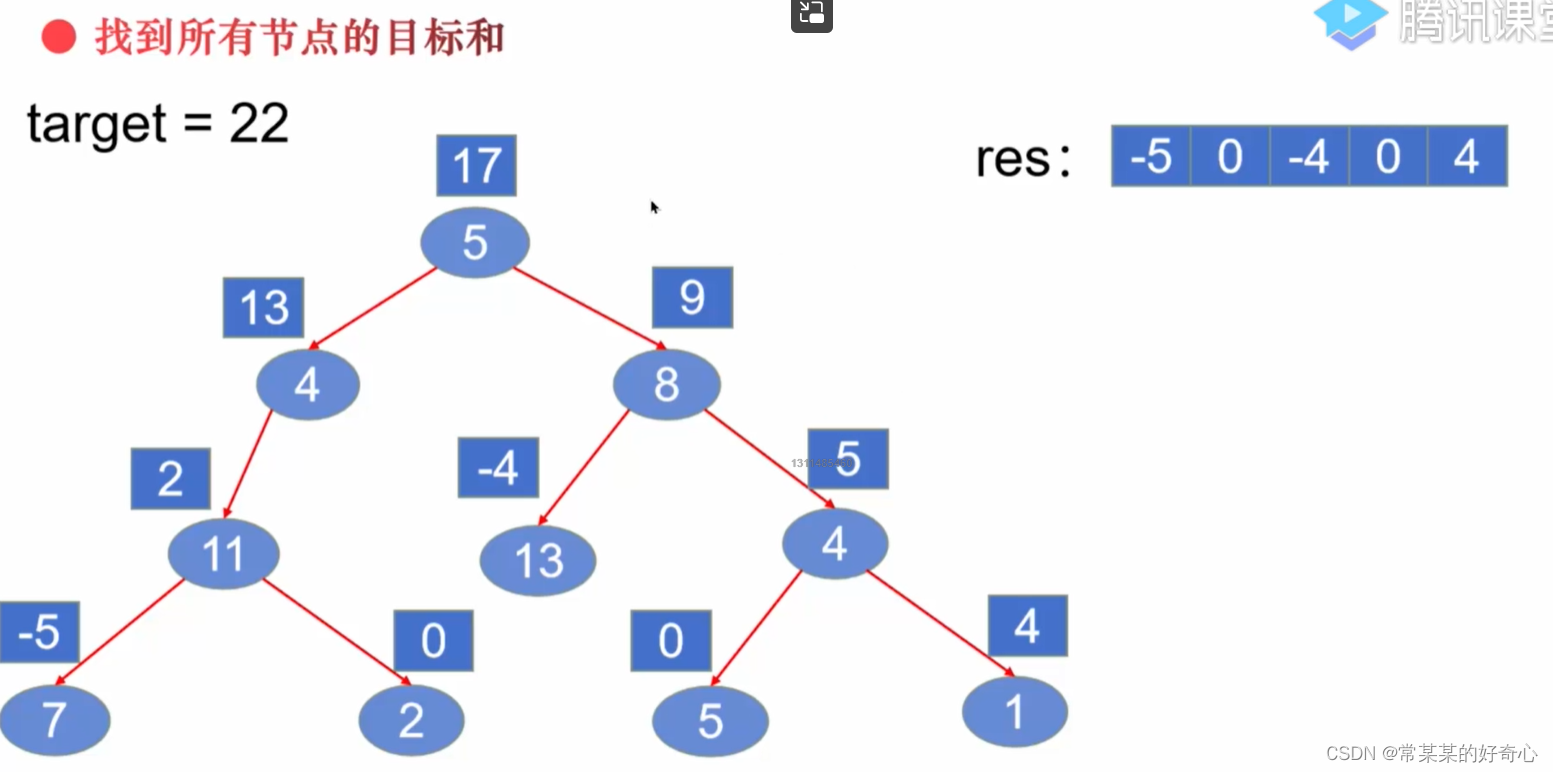
#方案一:回溯穷举所有路径+判断是否存在路径和
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
res=self.allpath(root)
for sinpath in res:
suma=sum(sinpath)
if suma==targetSum:return True
return False
def allpath(self,root):
self.res=[] #所有路径
path=[]
self.dfs(root,path)
return self.res
def dfs(self,node,path):
if not node:return None
#
path.append(node.val)
if not node.left and not node.right:
self.res.append(path.copy()) #path与res不能同一个对象
#
self.dfs(node.left,path)
self.dfs(node.right,path)
#在回溯过程中,将当前节点删去
del(path[-1]) #path.pop()
#方案二:计算每个路径和
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
res=self.allpath(root)
for val in res:
if val==targetSum:return True
return False
def allpath(self,root):
self.res=[] #所有路径和
self.dfs(root,0)
return self.res
def dfs(self,node,parantpathsum):
if not node:return
#
currpathsum=parantpathsum+node.val
if not node.left and not node.right:
self.res.append(currpathsum) #path与res不能同一个对象
#
self.dfs(node.left,currpathsum)
self.dfs(node.right,currpathsum)
#方案四:计算每个目标和
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
res=self.allpath(root,targetSum)
for val in res:
if val==0:return True #val==targetSum
return False
def allpath(self,root,target):
self.res=[] #所有路径和
self.dfs(root,target)
return self.res
def dfs(self,node,parantpathT):
if not node:return
#
currpathT=parantpathT-node.val
if not node.left and not node.right:
self.res.append(currpathT)
#
self.dfs(node.left,currpathT)
self.dfs(node.right,currpathT)
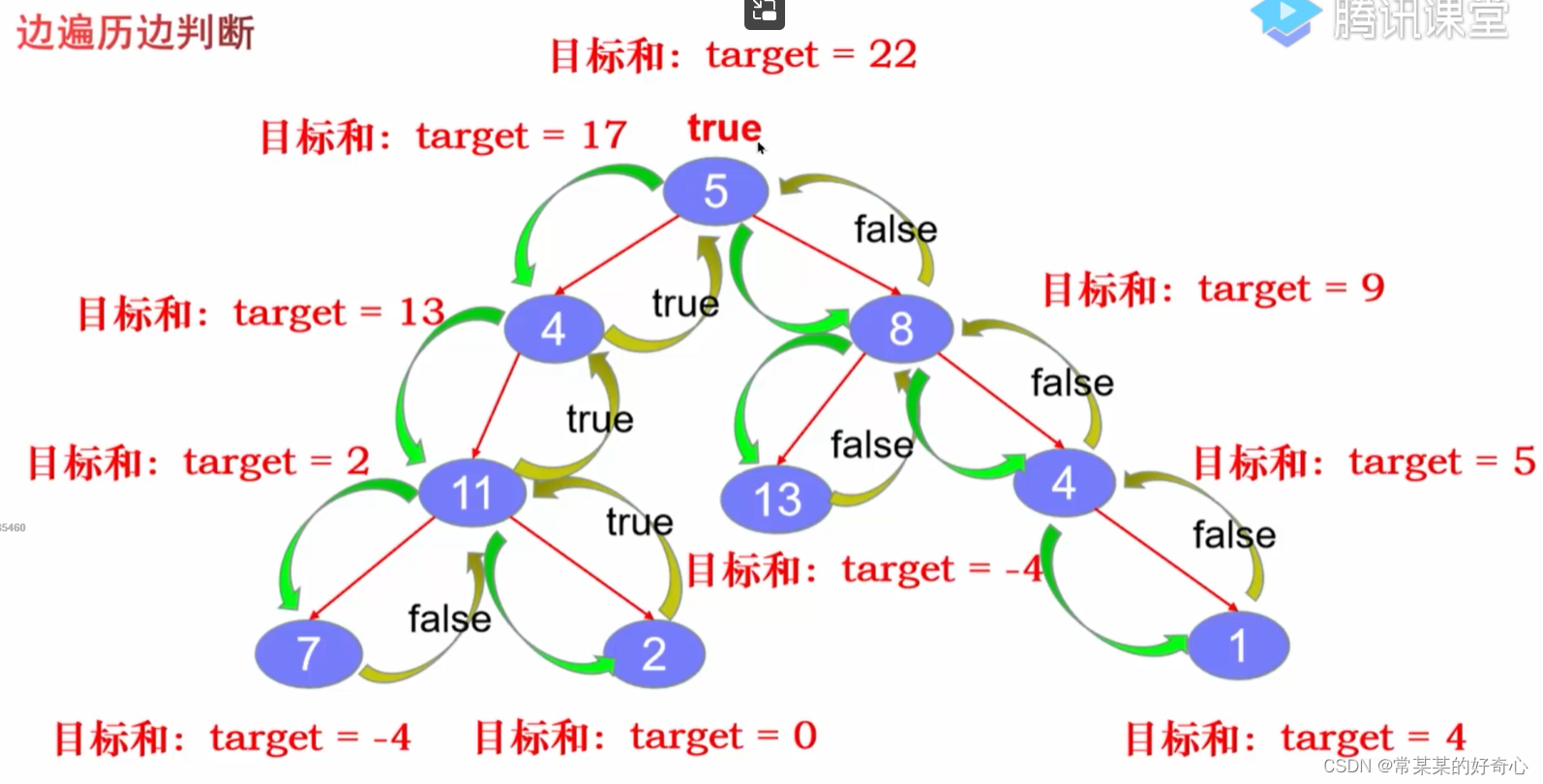
#方案五:计算每个节点的目标和+提前返回(边遍历边判断)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
return self.dfs(root,targetSum)
def dfs(self,node,parantpathT):
if not node:return False
#
currpathT=parantpathT-node.val
if not node.left and not node.right:
return currpathT==0
#
left=self.dfs(node.left,currpathT)
if left:return True
right=self.dfs(node.right,currpathT)
return left | right
lc 113【剑指 34】:路径总和 II
https://leetcode.cn/problems/path-sum-ii/
提示:
树中节点总数在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000
#方案一:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
if not root:return []
return self.allpath(root,targetSum)
def allpath(self,node,targetSum):
self.res=[]
path=[]
self.dfs(node,path,targetSum)
return self.res
def dfs(self,node,path,targetSum):
if not node:return
#
path.append(node.val)
if not node.left and not node.right:
if sum(path)==targetSum: #key
self.res.append(path.copy())
#
self.dfs(node.left,path,targetSum)
self.dfs(node.right,path,targetSum)
del(path[-1])
#方案二:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
if not root:return []
return self.allpath(root,targetSum)
def allpath(self,node,targetSum):
self.res=[]
path=[]
self.dfs(node,path,targetSum)
return self.res
def dfs(self,node,path,parantpathT):
if not node:return
#
path.append(node.val)
currpathT=parantpathT-node.val
if not node.left and not node.right:
if currpathT==0: #key
self.res.append(path.copy())
#
self.dfs(node.left,path,currpathT)
self.dfs(node.right,path,currpathT)
del(path[-1])
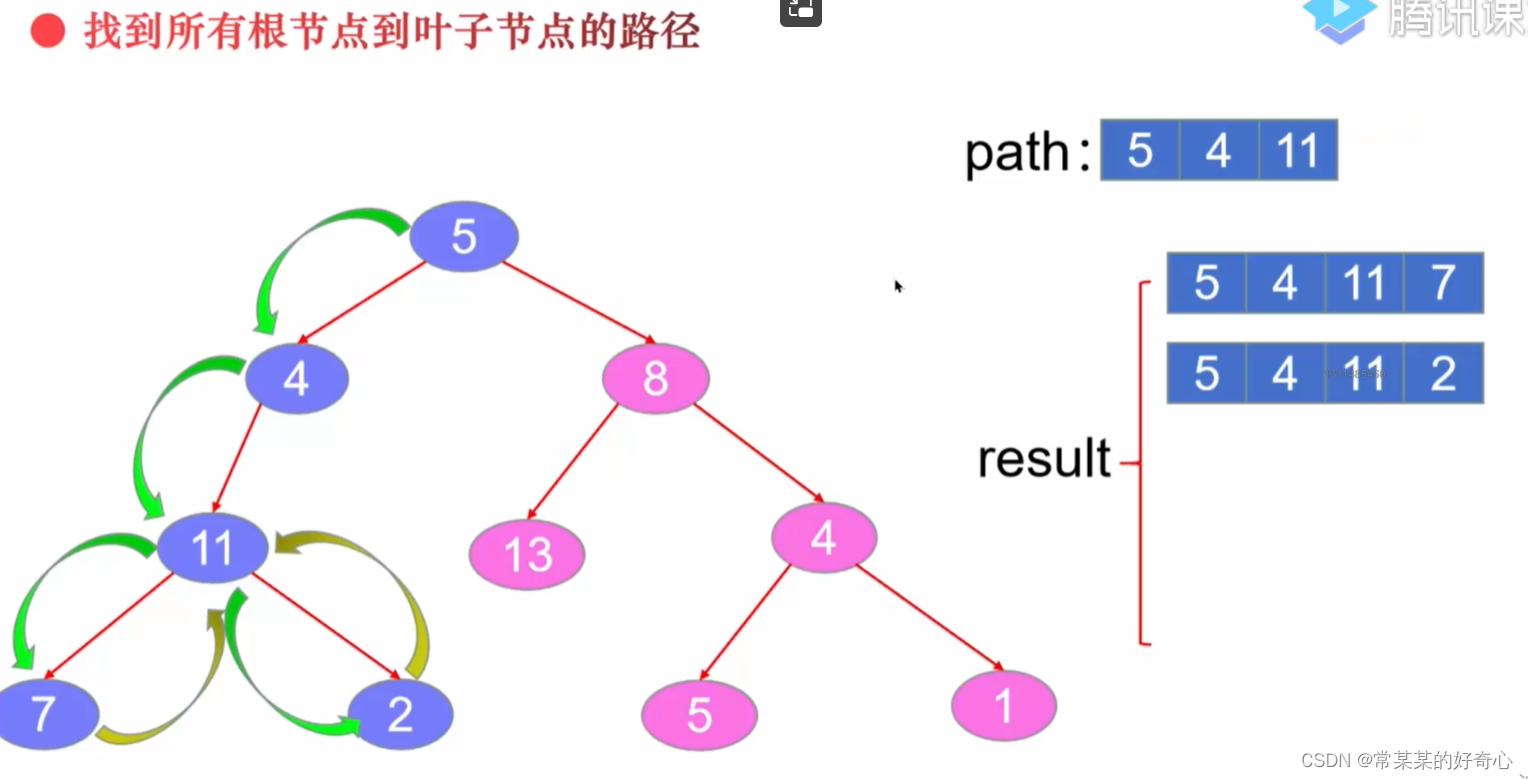
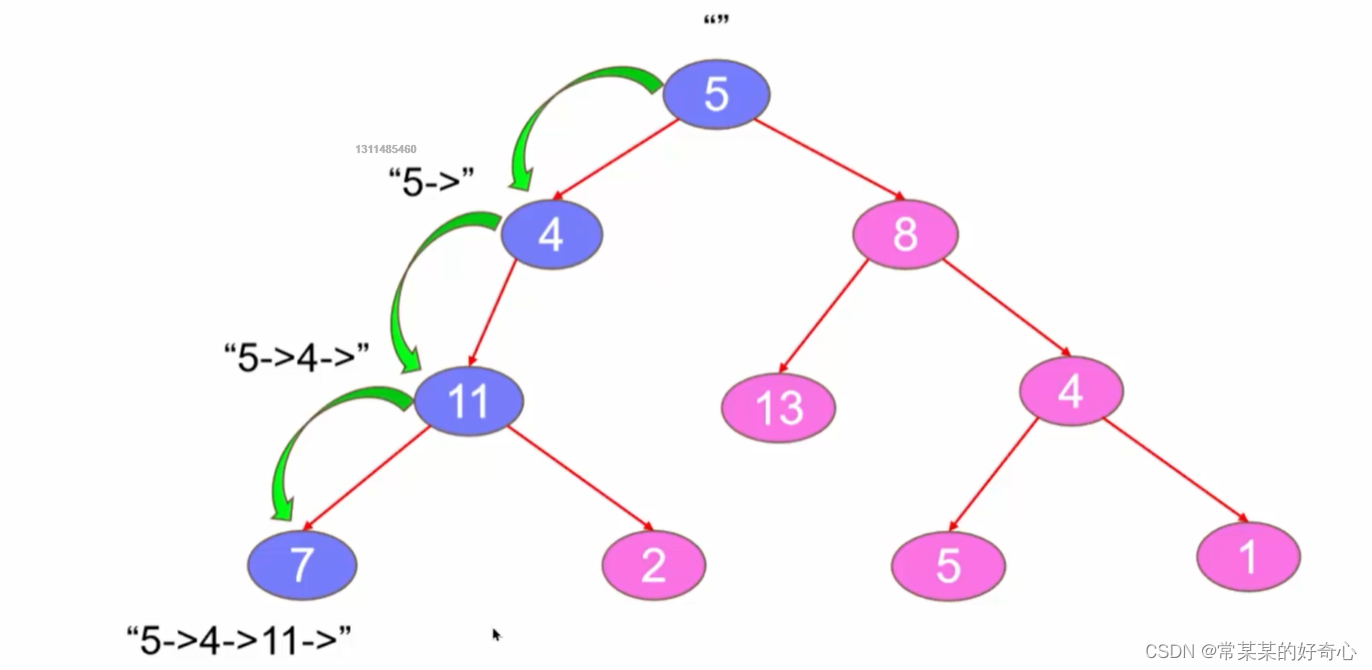
lc 257 :二叉树的所有路径
https://leetcode.cn/problems/binary-tree-paths/
提示:
树中节点的数目在范围 [1, 100] 内
-100 <= Node.val <= 100
#DFS
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
res=[]
self.dfs(root,'',res)
return res
def dfs(self,node,parantpath,res):
if not node:return
#
if not node.left and not node.right:
res.append(parantpath+str(node.val))
parantpath+=str(node.val)+'->' #key:位置
self.dfs(node.left,parantpath,res)
self.dfs(node.right,parantpath,res)
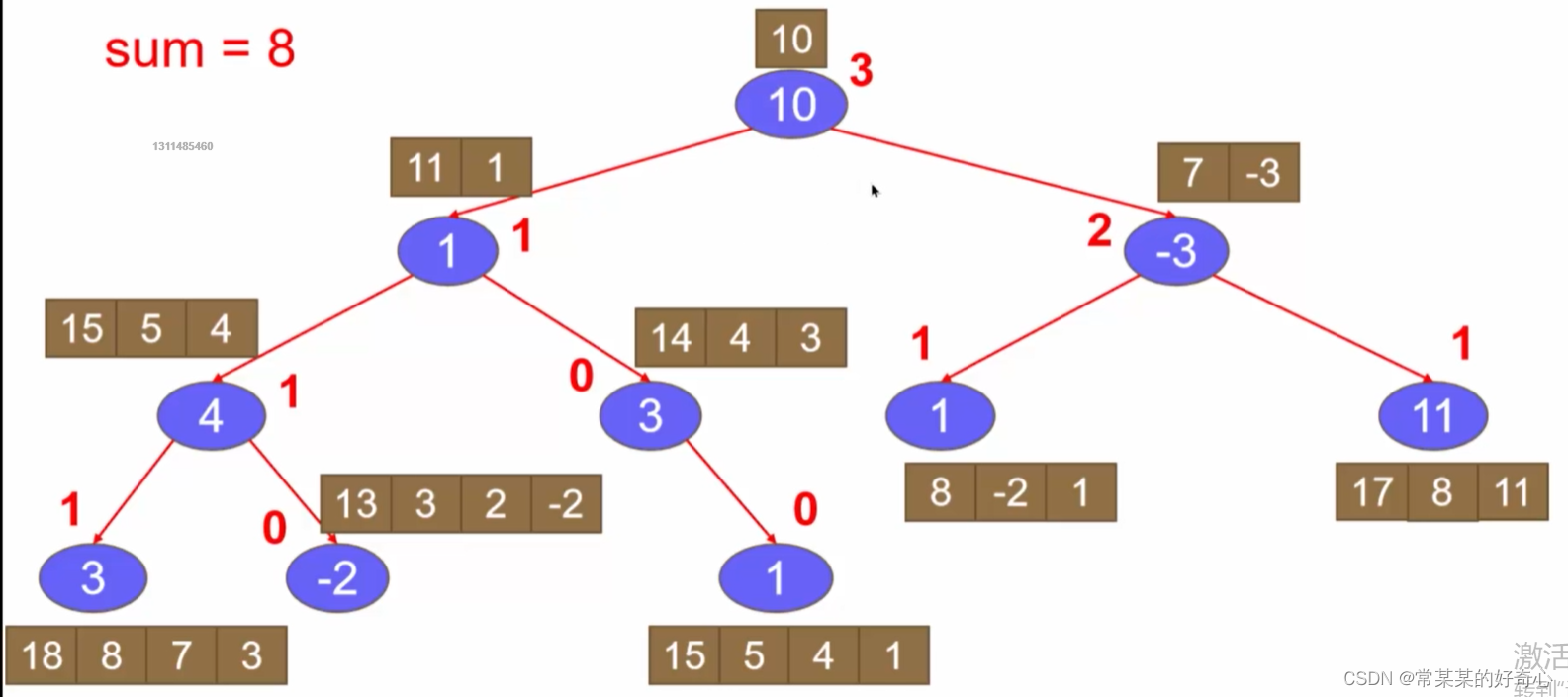
lc 437 【top100】:路径总和 III
https://leetcode.cn/problems/path-sum-iii/
提示:
二叉树的节点个数的范围是 [0,1000]
-10^9 <= Node.val <= 10^9
-1000 <= targetSum <= 1000
#方案一:DFS 计算所有路径和
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int:
#o(nlogn)
return self.dfs(root,list(),targetSum)
def dfs(self,node,parentpathsum,targetSum):
if not node:return 0
#key-key-key
#o(logn)
tmp=[]
cnt=0
for i in range(len(parentpathsum)):
num=parentpathsum[i]+node.val
tmp.append(num)
if num==targetSum:
cnt+=1
tmp.append(node.val)
if node.val==targetSum:
cnt+=1
#
leftcnt=self.dfs(node.left,tmp,targetSum)
rightcnt=self.dfs(node.right,tmp,targetSum)
return cnt+leftcnt+rightcnt
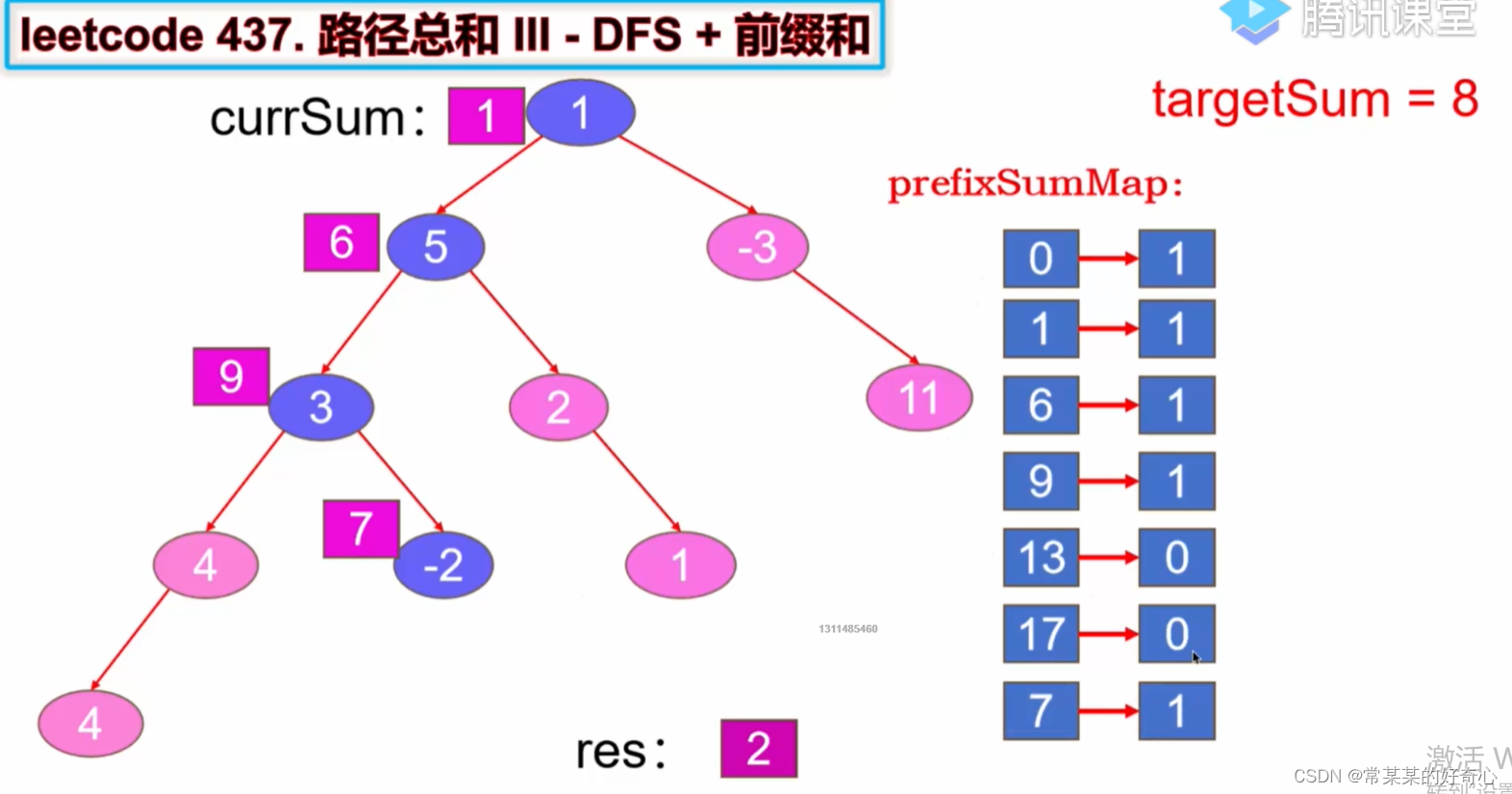
#方案二:DFS(前序)+前缀和(优化)
#O(n)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int:
self.res=0
self.dfs(root,0,targetSum,{0:1})
return self.res
def dfs(self,node,currsum,targetSum,prefixsum):
if not node:return
#key-key-key
currsum+=node.val
self.res+=prefixsum.get(currsum-targetSum,0)
prefixsum[currsum]=prefixsum.get(currsum,0)+1 #注意:先后位置(0-1-2-4-4)
#
self.dfs(node.left,currsum,targetSum,prefixsum)
self.dfs(node.right,currsum,targetSum,prefixsum)
#key:回溯时,更新prefixsum
prefixsum[currsum]=prefixsum.get(currsum)-1
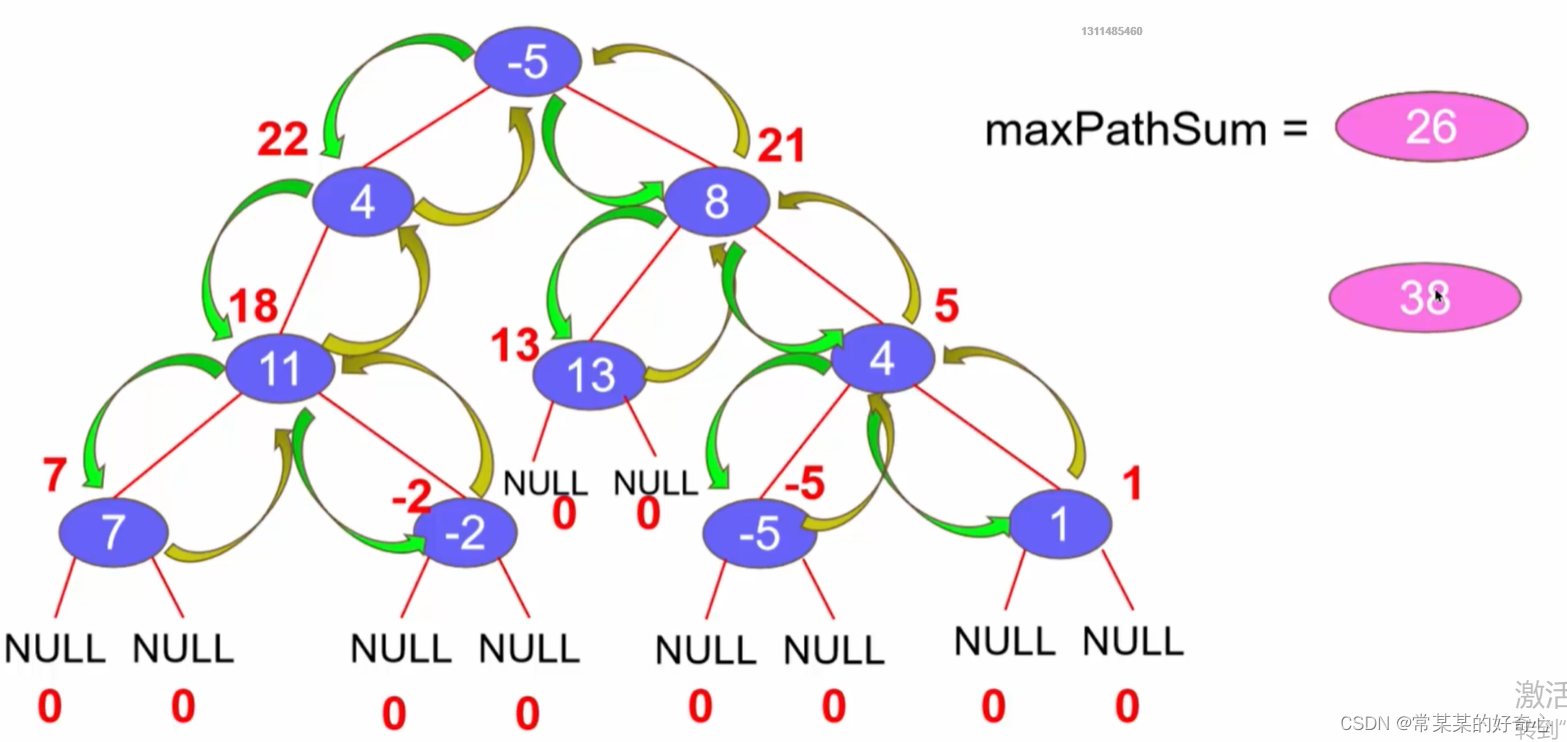
lc 124【top100】:二叉树中的最大路径和
https://leetcode.cn/problems/binary-tree-maximum-path-sum/
提示:
树中节点数目范围是 [1, 3 * 10^4]
-1000 <= Node.val <= 1000
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxPathSum(self, root: Optional[TreeNode]) -> int:
self.maxpathmax=float('-inf')
self.dfs(root)
return self.maxpathmax
#key:区别最大收益值与最大路径和
def dfs(self,node):
if not node:return 0
#
leftgain=max(self.dfs(node.left),0)
rightgain=max(self.dfs(node.right),0)
#节点相关的最大路径和
self.maxpathmax=max(self.maxpathmax,leftgain+rightgain+node.val)
#节点的最大收益值
return max(leftgain,rightgain)+node.val
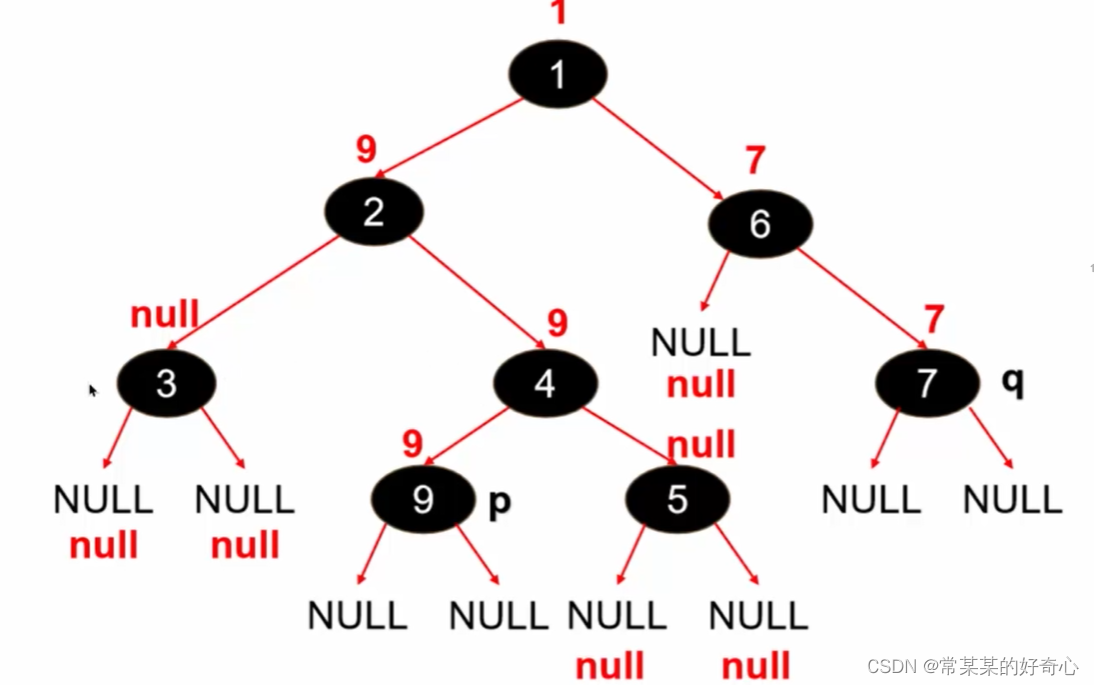
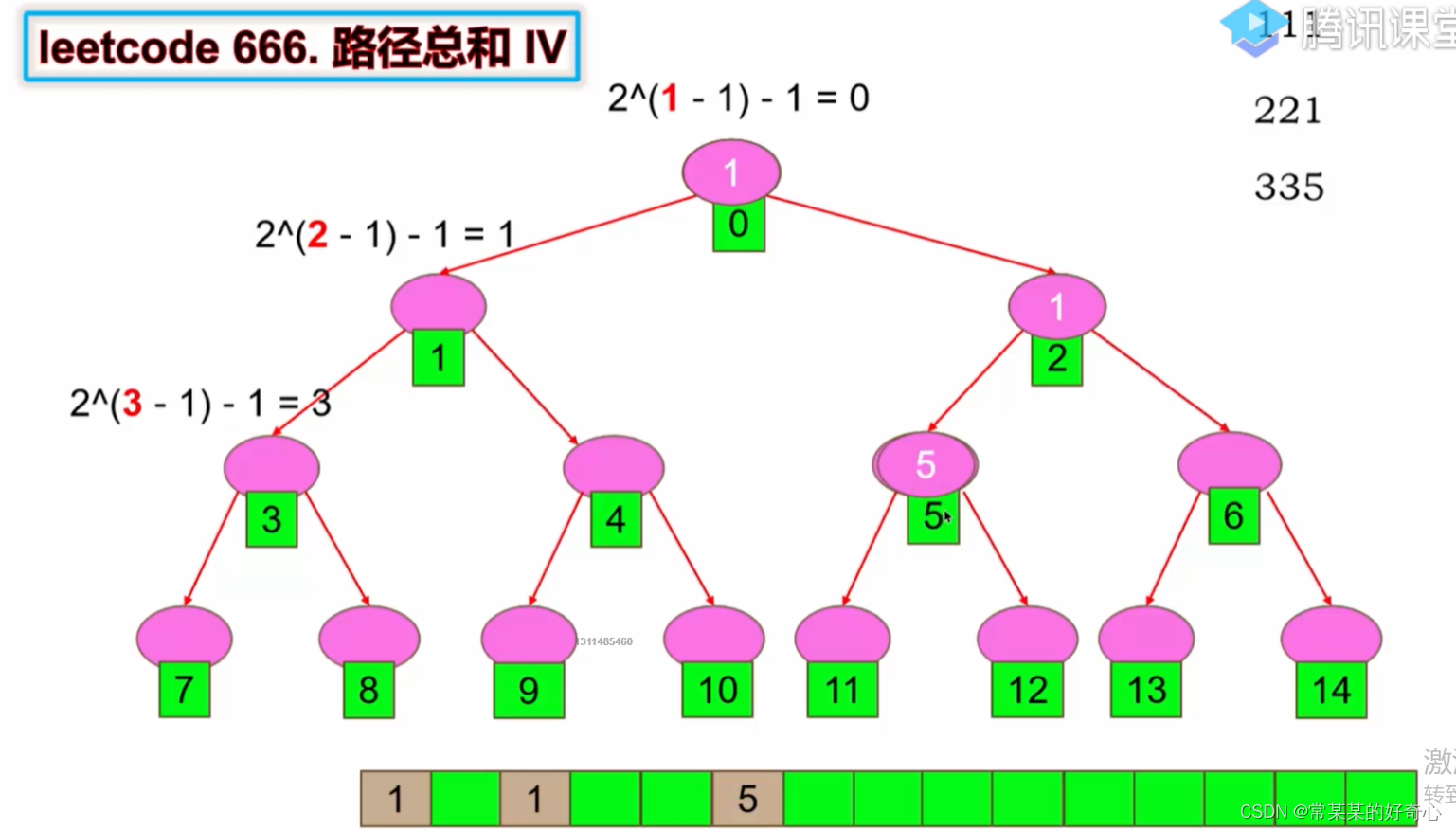
lc 666 :路径总和 IV
https://leetcode.cn/problems/path-sum-iv/
提示:
1 <= nums.length <= 15
110 <= nums[i] <= 489
nums 表示深度小于 5 的有效二叉树
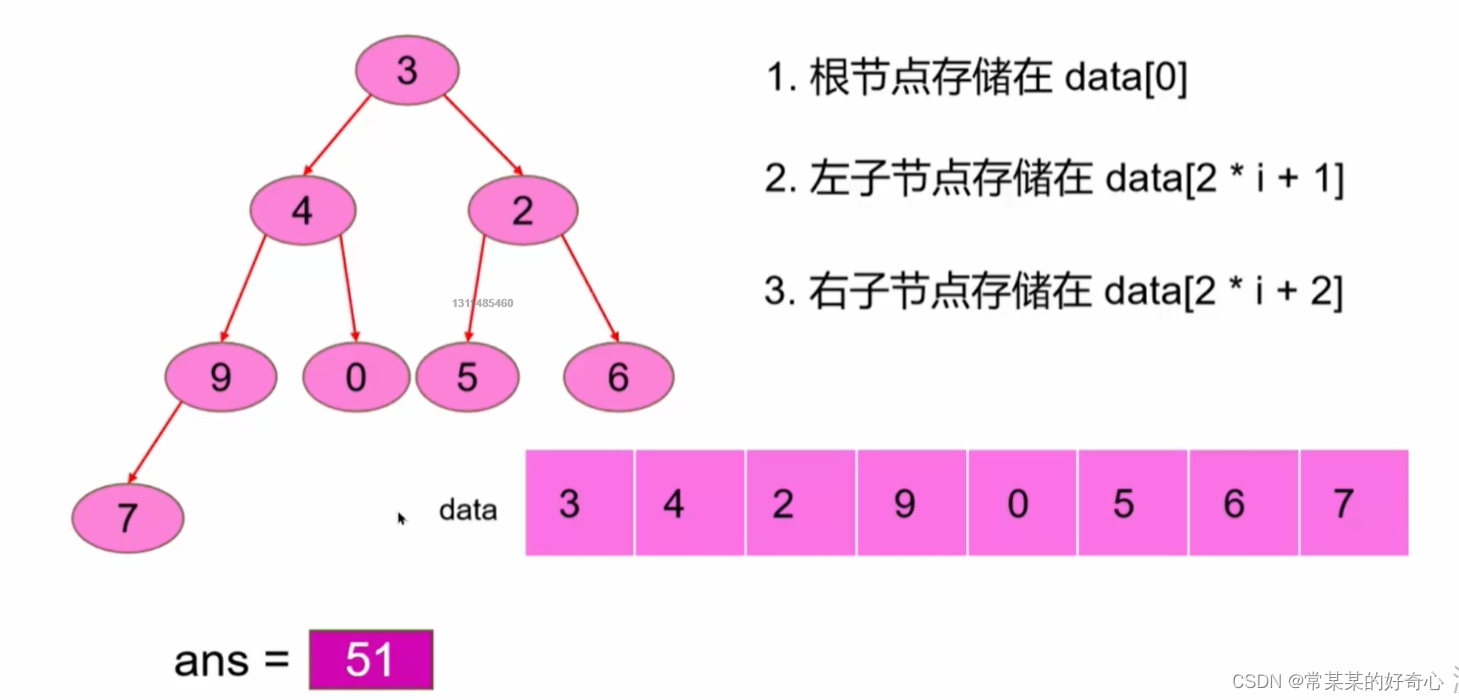
#树的构建->数组
class Solution:
def pathSum(self, nums: List[int]) -> int:
#buildtree
tree=[-1]*15
for n in nums:
bai=n//100
shi=n%100//10
ge=n%10
#
index=((1<<(bai-1))-1)+(shi-1)
tree[index]=ge
#求路径和
self.pathsum=0
self.dfs(tree, 0, 0)
return self.pathsum
def dfs(self,tree,i,currsum):
if tree[i]==-1:return
#key
currsum+=tree[i]
if i>=7 or (tree[2*i+1]==-1 and tree[2*i+2]==-1):
self.pathsum+=currsum
return #key
#
self.dfs(tree, 2*i+1, currsum)
self.dfs(tree, 2*i+2, currsum)